基于双树复小波和深度信念网络的轴承故障诊断

张淑清 胡永涛 姜安琦 李军锋 宿新爽 姜万录

1.燕山大学电气工程学院,秦皇岛，066004 2. 中南大学信息科学与工程学院，长沙，4100063. 燕山大学机械工程学院,秦皇岛，066004

基于双树复小波和深度信念网络的轴承故障诊断

张淑清1胡永涛1姜安琦2李军锋1宿新爽1姜万录3

1.燕山大学电气工程学院,秦皇岛，066004 2. 中南大学信息科学与工程学院，长沙，4100063. 燕山大学机械工程学院,秦皇岛，066004

提出了一种基于双树复小波(DTCWT)和深度信念网络(DBN)的轴承故障诊断新方法。采用DTCWT对轴承振动信号进行分解实验，结果表明DTCWT能够很好地将信号分解到不同频带。进而提取能量熵作为故障特征，采用DBN小样本分类模型对轴承故障进行分类，并与传统分类器进行比较，结果表明该方法能准确识别不同故障类型，扩展了DBN在机械故障诊断中的应用。

双树复小波；深度信念网络；受限波尔兹曼机；故障诊断

0 引言

机械故障诊断是保证生产系统安全稳定运行和提高产品质量的重要手段，其研究的关键在于信号特征提取和模式识别[1]。小波变换在信号特征提取中得到大量成功应用，但实小波变换存在有平移敏感性、方向性差、缺乏相位信息等缺点。双树复小波(dual-tree complex wavelet transform, DTCWT)是一种改进的复小波，采用双树结构保证信号完美重构，具有平移不变性、抑制频率混叠、有限冗余度和高效计算能力等优点[2]。机械振动信号包含大量谐波信号，DTCWT抑制频率混叠的特性能够保证信号被很好地分解为不同频带，有利于不同频带信号的特征提取。

机械故障模式识别属于典型的小样本识别问题[3]，SVM在解决小样本识别问题方面有突出优点[4]，然而SVM存在参数优化问题，惩罚系数和核函数参数的选取严重影响分类性能。随着人工智能研究的深入，深度学习得到了广泛研究[5]；深度网络是一种模拟人脑处理信息、具有多隐层多感知器的神经网络，其成果已成功应用于图像识别、语音处理、文本处理等[6-8]，但是这些应用均是针对大数据的，在小样本识别中应用较少。深度信念网络(deep belief network, DBN)是由多层受限玻尔兹曼机(restricted Boltzmann machines, RBM)堆叠而成的一种典型的深度网络结构，采用预训练和微调的训练方式，有效避免了参数选取的难题，同时只需少量样本便能训练出很好的分类器，在小样本识别中具有明显优势。

本文采用DTCWT将机械振动信号分解到不同频带，提取各频带能量熵能作为故障特征，结合DBN小样本分类器实现轴承故障诊断，对轴承的不同部位和不同损伤程度进行了实验。

1 DTCWT能量熵

DTCWT采用两棵并列的具有不同高通和低通滤波器组的实小波变换树实现，分别称为实树和虚树。信号在分解时实树和虚树滤波器组之间的延迟恰好是一个采样值的间隔，因此，双树二抽取得到的数据形成互补关系，减少了信息的丢失，使得DTCWT具有抑制频率混叠的特性，利于有效故障特征的提取。

为了表征不同故障，将能量熵引入故障特征提取中。当轴承发生故障时，各频带能量也随之变化，并且不同的故障能量变化也不同。熵包含了信号在动态变化中潜在的有用信息，熵值大小反映了信号概率分布的均匀程度，具有一定抗噪能力，将能量与熵相结合，提取能量熵作为轴承故障特征，能很好地反映轴承故障且计算简单。首先，对每个机械振动信号进行n层DTCWT分解，重构得到n+1个不同频带的分量。然后，计算每个分量每个采样点的能量Ei，根据下式计算每个分量的能量熵H：

(1)

得到n+1个特征向量。其中，εi为每个采样点的能量占该频带总能量的比重，m为每个频带的采样点数。

2 基于DBN的小样本分类

2.1 DBN小样本分类器

机械故障分类属于典型的小样本分类问题，为了解决小样本分类问题，基于DBN[9]设计了小样本分类器模型，如图1所示。该模型由两层RBM构成，每层RBM由可见层(visible, V)和隐含层(hidden, H)组成。由图2可以看出，V1和H1组成RBM1，H1(V2)和H2组成RBM2。V1为输入层，接收输入特征X，并对其进行编码后传输给H1，其节点数与输入特征维数相同。同时，H1又是RBM2的可见层，接收V1的输出，进行编码后传输给输出层H2，H1节点数对分类性能的影响不大，可根据经验确定。H2作为模型的输出，与标签层结合计算分类误差，其节点数与样本类别数相同。

图1 DBN小样本分类模型Fig.1 DBN classification model for small sample

DBN小样本分类模型的训练过程可分为预训练和微调两步。预训练采用无监督学习方式，由底向上逐层训练，重新编码输入特征，并获得各层的最初参数，如图1中实线箭头所示。微调为有监督学习，结合样本标签和预训练输出计算误差，采用BP算法，对预训练得到的最初参数进行细微调整，降低误差，从而使模型参数达到最优，如图1中虚线箭头所示。经过预训练和微调，模型便可对新数据进行分类识别。

2.2 预训练

预训练即对每层RBM由下向上单独训练，RBM是一种能量产生模型，所有的可见层单元与隐含层单元相连，同一层之间互不相连，如图2所示。其中，vi表示第i个可见层节点，hj表示第j个隐含层节点，Wij为vi与hj之间的连接权重，a和b分别为可见层和隐含层各节点的偏置。经过预训练可得到每层的最初参数θ=(ai,bj,wij)。

图2 RBM结构Fig.2 Structure of RBM

假设可见层和隐含层的节点为0或1的二值变量，给定状态(v,h)的能量[10]可表示为

(2)

(3)

其中，Z为归一化因子，可见层能量分布可通过所有隐含层相加得到：

(4)

由于同一层之间没有联系，所有的可见层节点之间相互独立，故vi=1的概率为

(5)

σ(x)=1/(1+e-x)

其中，σ(x)为Sigmoid函数，同理可得

(6)

RBM的训练目标是学习出参数θ，以拟合训练数据，通过求解训练集上的极大对数似然函数可得到θ，即

(7)

其中，T为训练样本个数，采用对比散度(contrastivedivergence,CD)[11]算法可得各参数的更新规则：

Δai=ε(〈ai〉data-〈ai〉recon)

(8)

Δbj=ε(〈bj〉data-〈bj〉recon)

(9)

Δwij=ε(〈vihj〉data-〈vihj〉recon)

(10)

其中，ε为学习效率，〈·〉data和〈·〉recon分别为当前模型及重构模型所定义的分布上的数学期望。

2.3 微调

由于预训练为无监督学习，经过预训练得到的最初参数并非模型的最佳参数，输出类别误差较大，为了提高模型分类性能，结合标签，采用BP算法对参数进行微调。

假设具有n个特征的一个样本x，通过可见层V1输入DBN，则该层输出为

(11)

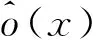
(12)

由式(11)可知输出类别与参数wij相关，通过BP算法对参数wij进行优化，即可得到最终的输出。

BP算法包括前向传播和后向传播两个过程，前向传播中输入被逐层传播到输出，得到预测的类别。后向传播将样本标签与预测的类别进行比较后得到误差err，err被逐层向后回传并通过梯度下降算法微调DBN的参数。即

err=y-o

(13)

综上分析，DBN小样本分类模型的参数包括输出参数θ、每层的节点数、学习效率和迭代次数，以上参数都可根据公式和经验快速确定，避免了传统分类器参数选取的难题。

3 实验分析

3.1 振动信号分解

DTCWT具有抑制频率混叠的特性，能够对机械振动信号进行有效的分解，保证各频带信息完备准确。为了验证该特性，对轴承故障信号进行实验分析，实验数据来自于凯斯西储大学轴承故障数据，电机转速为1750 r/min，负荷为1.47 kW，采样频率为12 kHz，采样时间为0.1 s。研究内圈0.1778 mm(0.007英寸)损伤状态。

采用DTCWT对故障信号进行三层分解和重构获取不同频带特征信息，同时与离散小波变换(discrete wavelet transform, DWT)进行对比研究。分别采用DTCWT和DWT分解故障信号，各频带频率特性如图3、图4所示。图3中从上到下分别为高频分量d1、d2、d3和低频分量a3。图3采用DTCWT分解重构，可以看出其低频分量明确，高频分量仅在d1和d2中存在少量混叠，信号被很好地分解到不同频带。图4为DWT分解重构结果，可以看出其低频分量完全混叠在高频分量d3中，同时高频分量d1、d2和d3之间也存在严重混叠现象。因此，DWT不能将信号进行有效分离，而DTCWT能对机械振动信号进行完美分解重构，为机械故障类型识别提供了良好的特征。

图3 故障信号DTCWT分解各频带频率特性Fig.3 Frequency characteristics of each frequency bands of fault signal decomposed by DTCWT

图4 故障信号DWT分解各频带频率特性Fig.4 Frequency characteristics of each frequency bands of fault signal decomposed by DWT

3.2 DBN小样本分类实验

DBN小样本分类器具有参数易选取和对训练集要求低的优点，为了验证该特性，对Iris数据集进行分类研究，并与SVM进行对比。将Iris分为训练集和测试集，其中测试集每类有25个样本，训练集每类样本数为1、2、3、4、5、6、7、8、9、10、15、25，对不同训练集均进行10次实验，取平均分类准确率作为最终结果。DBN小样本分类器由两层RBM构成，V1、H1和H2层的节点数分别为4、4和3，根据经验，训练迭代次数取100，学习速率取0.01，采用SVM进行对比研究，SVM选用径向基核函数，其系数均为默认值。图5所示为测试准确率随训练集样本个数变化的关系，可以看出，当每类具有1个样本时，DBN和SVM测试准确率分别为73.87%和60.33%，远不能满足分类要求。当训练集每类样本个数为4时，DBN测试准确率达到93.47%，基本满足分类要求，而SVM测试准确率为88.9%。之后随着训练集样本个数的增多，DBN测试准确率逐渐提高，最终稳定在97.33%，这表明适当增加训练集个数有利于DBN训练，能够提高DBN分类准确率。而SVM测试准确率并没有随样本个数增加而增加，训练集样本中每个样本个数为15时SVM测试准确率达到最高值96%，而训练集样本中每个样本个数为25时SVM测试准确率降至94.67%，这表明SVM对训练集样本数要求较高。由此可见，对于小样本识别，DBN优于SVM，需要较少的训练集便可以训练出较好的分类网络，且训练集越大，分类能力越强。

图5 测试准确率随训练集样本个数的变化Fig.5 The relationship between the test accuracy and the samples number of training set

3.3 轴承故障诊断实验

为了验证本文方法在故障诊断中的有效性和优越性，对轴承正常状态(n)、内圈不同程度损伤(ir007，ir014，ir021)、滚动体不同程度损伤(b007，b014，b021)和外圈不同程度损伤(or007，or014，or021)共十种状态进行故障诊断。

每种状态取100个样本，对十种状态的每个样本进行DTCWT三层分解并进行单支重构，得到4个频带的分量，计算每个分量的能量熵作为特征向量，10种状态共得到1000×4的特征向量，以a3分量为例，10种状态的能量熵如图6所示，由图6可以判断出正常状态和故障状态，但是b007、b014、b021和or014四种故障之间相互重叠，且or021特征比较复杂，即滚动体不同程度损伤和外圈不同程度损伤不能被直观判断，因此，采用DBN进行分类识别。

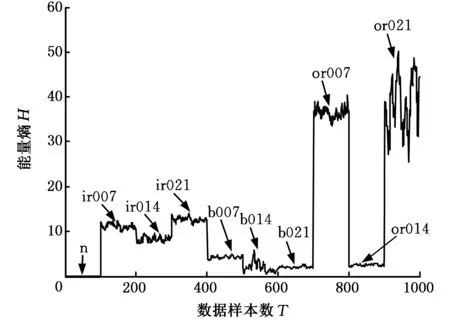
图6 a3分量十种状态的能量熵Fig.6 Energy entropy of a3 component of ten states

为了验证DBN在小样本识别上的优势，将样本分为训练集和测试集：各状态分别取3、5、10、20、30、40、50个样本作为训练集，各状态取50个样本作为测试集。为了增强分类结果的可信性，取10次实验结果的平均值作为最终结果。DBN由2层RBM构成，V1、H1和H2层的节点数分别为6、10和10，根据经验，训练迭代次数取100，学习速率取0.01，以SVM作为对比，不同训练集的测试结果如图7所示。由图7可以看出DBN分类效果明显优于SVM，只取3个样本便可以训练出一个很好的DBN分类器，其分类准确率可达到93.44%；而SVM分类准确率只有80.42%，说明DBN有更好的学习特征。随着训练集样本的增加，DBN分类准确率随之提高，而SVM在各状态取30个样本时分类准确率最高，随着样本的增加，分类准确率减小，说明样本越多DBN学习能力越强，分类准确率越高；而SVM对样本个数要求较高，样本个数过多或过少都会导致分类准确率降低。

图7 不同训练集的测试结果Fig.7 Test result of different training sets

为了进一步验证DBN分类效果，对每种状态的分类准确率进行研究，并与经典分类器(BP神经网络和SVM)进行对比，这里重点研究滚动体和外圈不同程度损伤。训练集各状态样本个数为30，各分类器对不同状态的分类准确率见表1，可以看出DBN的分类准确率均高于BP和SVM的分类准确率；并且对于特征比较复杂的or021，DBN分类准确率为100%，而BP和SVM分别为90%和92%，这表明DBN能更好地处理特征，识别故障类型。

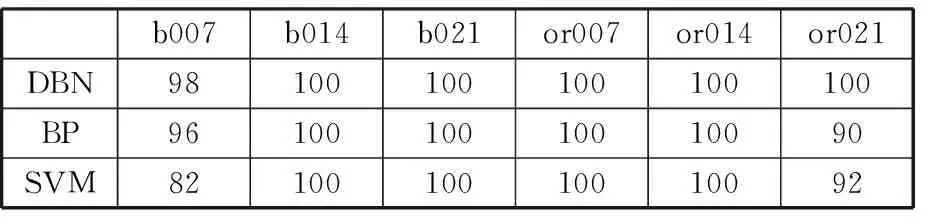
表1 不同分类器对不同状态的分类准确率Tab.1 Classification for different states of different classifiers %

各状态取30个样本，进一步研究DBN的训练效率。图8所示为训练集的均方误差随训练迭代次数的变化，可以看出，在前20次迭代中，均方误差随着迭代次数的增加迅速减小，迭代20次时，均方误差已小于0.1。随后，随迭代次数的增加，均方误差逐步减小并趋于稳定。迭代40次时，均方误差减小到0.01，此时的分类准确率可达99%。因此，应合理确定DBN训练迭代次数，若迭代次数太少，则分类准确率低；而迭代次数过多不但不会明显提高分类准确率，反而浪费训练时间。

图8 均方误差变化曲线Fig.8 Variation curve of mean square error

4 结论

(1) DTCWT具有平移不变性，能有效避免扰动信号的影响，较好地对机械振动信号分解和重构，DTCWT能量熵能很好地表征机械振动信号的特征。

(2)在机械故障诊断中DBN仅需少量训练样本便能很好地识别不同故障类型，识别准确率随着训练样本的增加而提高，并且对复杂的特征具有很好的辨识能力。

(3)迭代次数影响DBN识别准确率，为便于观察结果，根据经验设置较大的迭代次数，在实际应用中，若迭代次数过大则容易浪费时间，故应根据实际情况，通过实验确定最佳迭代次数。

[1] 秦大力, 于德介. 基于本体的机械故障诊断贝叶斯网络[J]. 中国机械工程, 2013, 24(9): 1195-1209. QIN Dali, YU Dejie.Ontology-based Diagnostic Bayesian Networks for Mechanical Fault Diagnosis[J].China Mechanical Engineering, 2013, 24(9): 1195-1209.

[2] 艾树峰. 基于双树复小波变换的轴承故障诊断研究[J]. 中国机械工程, 2011, 22(20): 2446-2451. AI Shufeng. Research on Bearing Fault Diagnosis Based on Dual-tree Complex Wavelet Transform[J].China Mechanical Engineering, 2011, 22(20): 2446-2451.

[3] 李鑫滨, 陈云强, 张淑清. 基于改进ABC算法优化的LSSVM多分类器组机械故障诊断模型[J].中国机械工程, 2013, 24(16): 2157-2164.LIXinbin,CHENYunqiang,ZHANGShuqing.MechanicalFaultDiagnosisModelBasedonImprovedABCAlgorithmOptimizedMultipleLSSVMClassifierGroup[J].ChinaMechanicalEngineering, 2013, 24(16): 2157-2164.

[4]HARISHN,LOKESHA,MANDALS,etal.ParameterOptimizationUsingGAinSVMtoPredictDamageLevelofNon-reshapedBermBreakwater[J].TheInternationalJournalofOceanandClimateSystems, 2014, 5(2)：79-88.

[5]ARELI,ROSEDC,KARNOWSKITP.DeepMachineLearning—aNewFrontierinArtificialIntelligenceResearch[J].IEEEComputationalIntelligenceMagazine,2010, 5(4): 13-18.

[6]BENGIOY.DeepLearningofRepresentationsforUnsupervisedandTransferLearning[J].UnsupervisedandTransferLearningChallengesinMachineLearning, 2012(27): 17-36.

[7]JINN,ZHANGJS,ZHANGCX.ASparse-responseDeepBeliefNetworkBasedonRateDistortionTheory[J].PatternRecognition, 2014, 47(9): 3179-3191.

[8]LAROCHELLEH,MANDELM,PASCANUR,etal.LearningAlgorithmsfortheClassificationRestrictedBoltzmannMachine[J].TheJournalofMachineLearningResearch, 2012, 13(1): 643-669.

[9]HINTONGE,OSINDEROS,TEHYW.AFastLearningAlgorithmforDeepBeliefNets[J].NeuralComputation, 2006, 18(7):1527-54.

[10]TOMCZAKJM,ZIEBAM.ClassificationRestrictedBoltzmannMachineforComprehensibleCreditScoringModel[J].ExpertSystemswithApplications, 2015, 42(4): 1789-1796.

[11]SHERIAM,RAFIQUEA,PEDRYCZW,etal.ContrastiveDivergenceforMemristor-basedRestrictedBoltzmannMachine[J].EngineeringApplicationsofArtificialIntelligence, 2015, 37: 336-342.

(编辑 陈 勇)

Bearing Fault Diagnosis Based on DTCWT and DBN

ZHANG Shuqing1HU Yongtao1JIANG Anqi2LI Junfeng1SU Xinshuang1JIANG Wanlu3

1.Institute of Electrical Engineering, Yanshan University, Qinhuangdao,Hebei ,066004 2.School of Information Science and Engineering, Central South University,Changsha,410006 3.Institute of Mechanical Engineering, Yanshan University, Qinhuangdao,Hebei ,066004

Based on DTCWT and DBN, a new method of bearing fault diagnosis was proposed. Experiments on bearing vibration signals decomposition show that the signals may be well decomposed into different frequency bands by DTCWT. Then, power entropy of different frequency bands were taken as the fault features and input to the model for classification and the traditional classifiers were taken as the comparison. Results show that the method may identify different fault types accurately, which expands the applications of DBN.

dual-tree complex wavelet transform (DTCWT);deep belief network (DBN);restricted Boltzmann machine (RBM);fault diagnosis

2016-06-16

国家自然科学基金资助项目(51475405，61077071)；河北省自然科学基金资助项目(F2015203413, F2016203496, F2015203392)

TN911.6

10.3969/j.issn.1004-132X.2017.05.005

张淑清，女，1966年生。燕山大学电气工程学院教授、博士研究生导师。主要研究方向为弱信号检测、智能信号处理、故障诊断等。发表论文50余篇。E-mail:zhshq-yd@163.com。胡永涛，男，1987年生。燕山大学电气工学院博士研究生。姜安琦，女，1995年生。中南大学信息科学与工程学院本科生。李军峰，男，1994年生。燕山大学电气工程学院硕士研究生。宿新爽，女，1993年生。燕山大学电气工程学院硕士研究生。姜万录，男，1964年生。燕山大学机械工程学院教授、博士研究生导师。