局部特征尺度分解和局部切空间排列在故障特征频率提取中的应用
王 斐 房立清 吕 岩
军械工程学院火炮工程系,石家庄,050003
局部特征尺度分解和局部切空间排列在故障特征频率提取中的应用
王 斐 房立清 吕 岩
军械工程学院火炮工程系,石家庄,050003
为了从非线性、非平稳的振动信号中提取故障特征频率,提出了一种故障特征频率提取新方法。该方法将局部特征尺度分解和流形学习算法局部切空间排列相结合,首先利用局部特征尺度分解将振动信号分解成若干个内禀尺度分量,将其组成多维特征向量;其次采用流形学习算法中的局部切空间排列对多维特征向量进行降维处理,得到低维特征向量,对得到的低维特征向量进行信号重构;最后采用频谱分析方法对重构信号进行故障特征频率的提取。在滚动轴承故障试验中,所提出方法能够准确提取出内圈和外圈故障的特征频率,验证了该方法的有效性。
局部特征尺度分解;局部切空间排列;故障频率;滚动轴承;频谱分析
0 引言
在机械故障诊断中,从振动信号中提取机械零件的故障特征频率是诊断的重要手段。但在机械运行过程中,一方面,由于系统转速不稳定、负荷变化以及各部件产生大量冲击、摩擦等作用,所获得的振动信号表现出非线性非平稳特性;另一方面,设备各零部件的结构和位置不同,运行速度各异,振动信号包含了不同零部件的各种特征频率,特别当故障较微弱时,其故障特征频率往往被其他零部件产生的运行振动和随机噪声信号所淹没[1]。传统的Fourier变换和以其为基础的短时Fourier变换,以及后来的Wigner-Ville分布等时频分析方法不能满足非线性和非平稳信号的分析需要[2];采用Hilbert变换的包络分析存在端点效应以及无法解释负频率等问题[3]。这给故障特征频率的提取带来很大困难。
局部特征尺度分解(local characteristic-scale decomposition,LCD)是一种新的信号处理方法,该方法能够将复杂的振动信号自适应地分解成一系列单分量的内禀尺度分量(intrinsic scale component,ISC),每个ISC又包含了不同尺度下的时域信息和频域信息;通过ISC分量可以有效地提取信号的故障特征信息[4-5]。
经LCD分解之后的振动信号包含多个ISC分量,如何选取合适的ISC分量是准确提取故障频率的重要方面。文献[6]通过比较各ISC分量与原始信号的相关性来确定合适的ISC分量,但该方法有可能遗失微弱的故障信息。流形学习法是一种基于微分几何与拓扑学的非线性高维数据处理方法,该方法可以有效地挖掘高维非线性数据内在几何分布特征,具有很好的非线性复杂信息处理能力,已被用于机械故障诊断提取领域[7]。LCD分解后得到的所有ISC分量可以看成一组包含多种信息的高维信号,采用流形学习方法对其进行降维,对降维后的信号进行重构,重构信号包含了故障信息的低维主特征,这样可以有效地提取微弱的故障特征频率。
基于上述分析,提出了一种新的故障特征频率提取方法——局部特征尺度分解和流形学习算法局部切空间排列(local tangent space alignment,LTSA)相结合的方法,并通过试验验证了该方法的有效性。
1 局部特征尺度分解方法
LCD方法假设任意一个复杂信号可以由不同的ISC分量组成,并且任意两个ISC分量之间相互独立,这样任意一个信号x(t)就可以被分解为有限个ISC分量之和,其中任何一个ISC分量满足如下两个条件[8]:
(1)在整个数据段内,任意两个相邻极值点的符号互异。
(2)在整个数据段内,所有极值点为Xk,极值点对应的时刻为τk(k=1,2,…,M;M为极值点的个数),由任意相邻两个极大(小)值点(τk,Xk)、(τk+2,Xk+2)连接成的线段在其中间极小(大)值点(τk+1,Xk+1)相对应时刻τk+1的函数值Ak+1与该极小(大)值Xk+1的比值关系近似不变。其中
(1)
以上两个条件能保证ISC分量具有局部对称性,且在任意两个相邻极值点之间具有单一模态。根据ISC的定义,可以对x(t)进行局部特征尺度分解,其分解过程如下[9-10]:
(1)确定x(t)的所有极值点Xk以及极值点对应的时刻τk。连续相邻的两个极值点可以将x(t)分成若干个区间,在任意两个相邻的极值点间直接对x(t)进行线性变换,得到
(2)
Lk+1=aAk+1+(1-a)Xk+1
(3)其中,Hk为对原信号第k个区间进行线性变换所得到的基线段信号。对于参数a,一般取值为0.5。
(2)将Hk连接得到H1(t),并将H1(t)从原始信号x(t)中分离出来,得到剩余信号P1(t)。理想地,如果P1(t)满足ISC分量的判据条件,则将P1(t)作为x(t)的第一个ISC分量SISC1(t)。如果不满足ISC分量的判据条件,则将P1(t)作为原始信号重复步骤(1),循环i次,直到得到内禀尺度分量Pi,Pi即为信号x(t)的第一个内禀尺度分量SISC1(t)。
(3)将SISC1(t)从原始信号x(t)中分离出来,得到一个新的信号r1,将r1作为原始信号重复步骤(1)、步骤(2),得到x(t)满足ISC判据条件的第2个分量SISC2(t),重复循环n次,得到n个满足ISC判据条件的分量,直到rn为一单调函数或者小于预设阈值为止。这样就可以将x(t)分解为n个ISC分量和一个余量rn之和,即
(4)
信号经LCD分解得到若干个ISC分量后,可以仿照EMD定义时频谱的方法定义LCD时频谱。对SISCi(t)进行Hilbert变换可以得到其瞬时幅值ai(t)和瞬时频率fi(t),这样就可以将x(t)的幅值表示到时间-频率的二维平面上。由此可以定义基于LCD的时频分布:
(5)
通过H(f,t)还可以定义基于LCD的边际谱h(f)和基于LCD的瞬时能量谱hE(t):
(6)
(7)
2 局部切空间排列
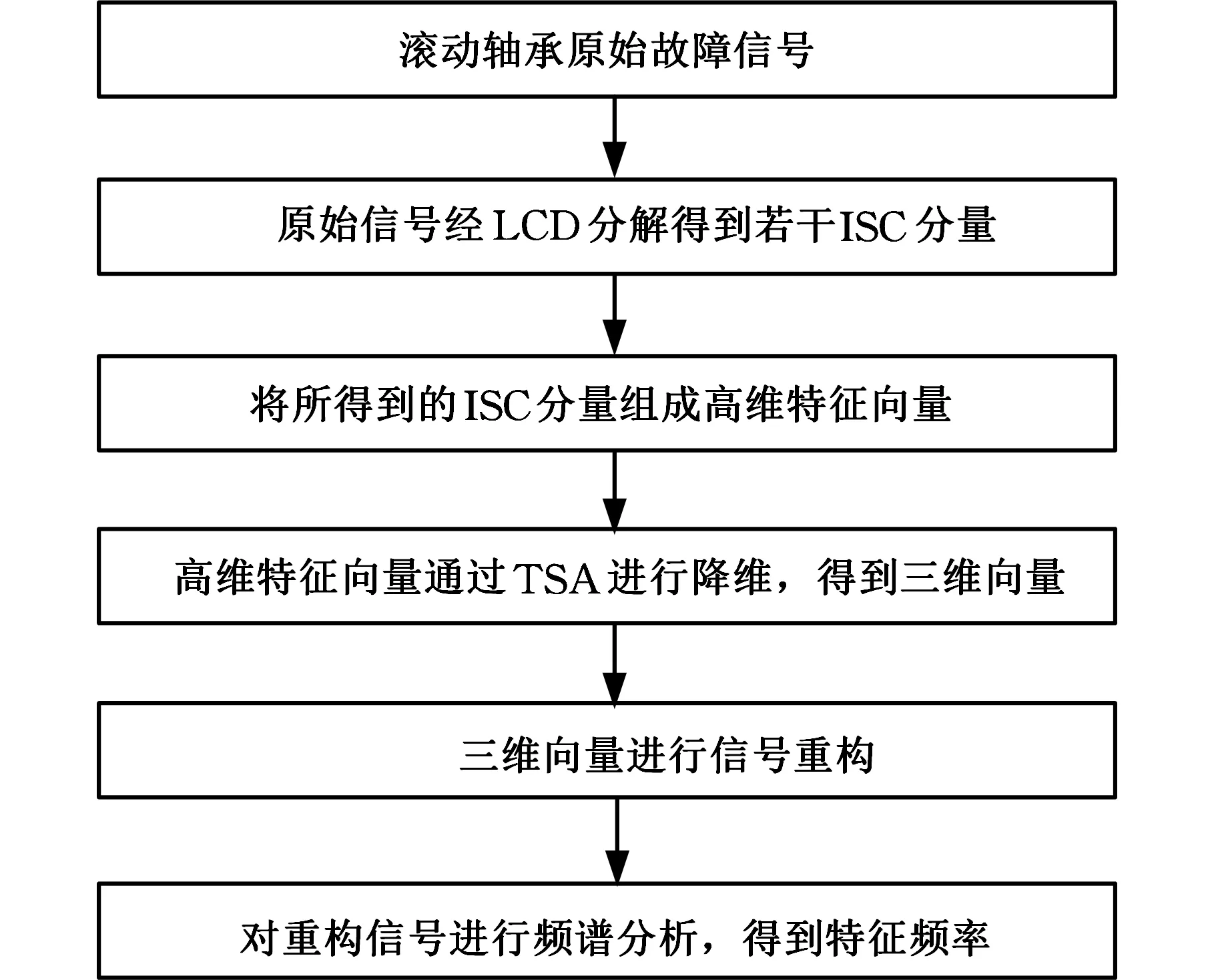
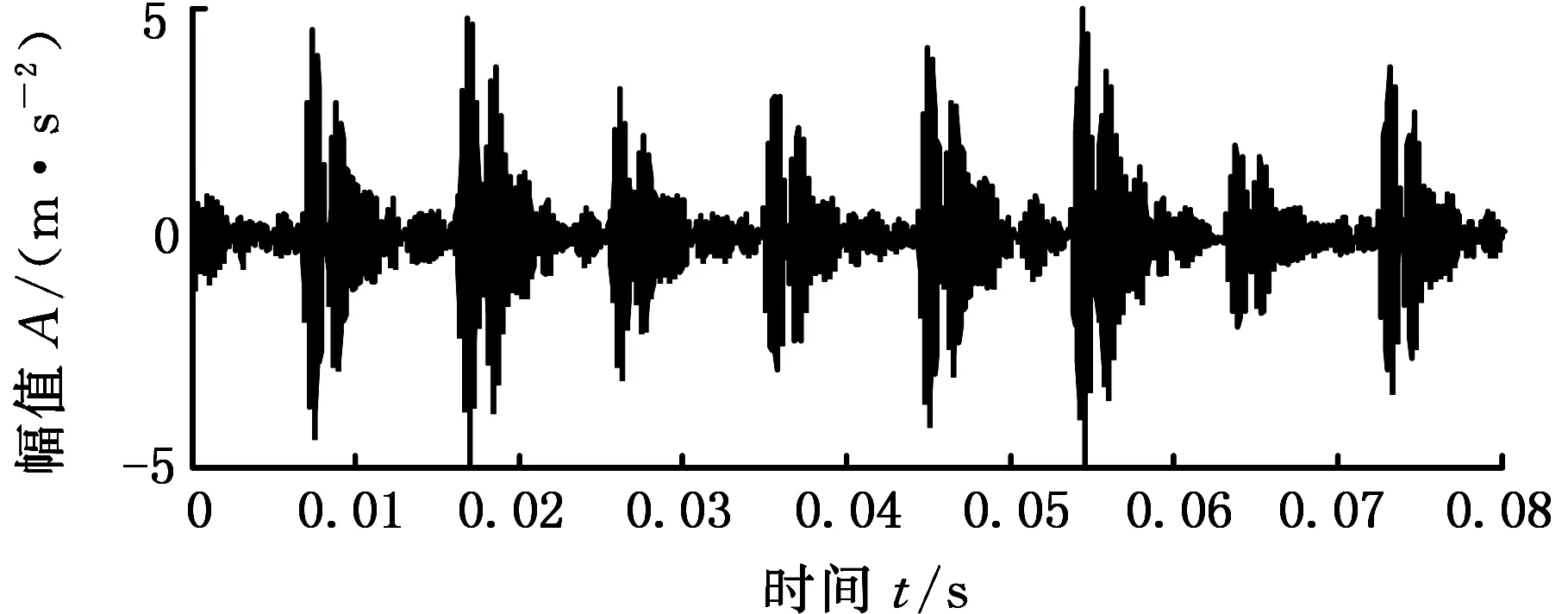
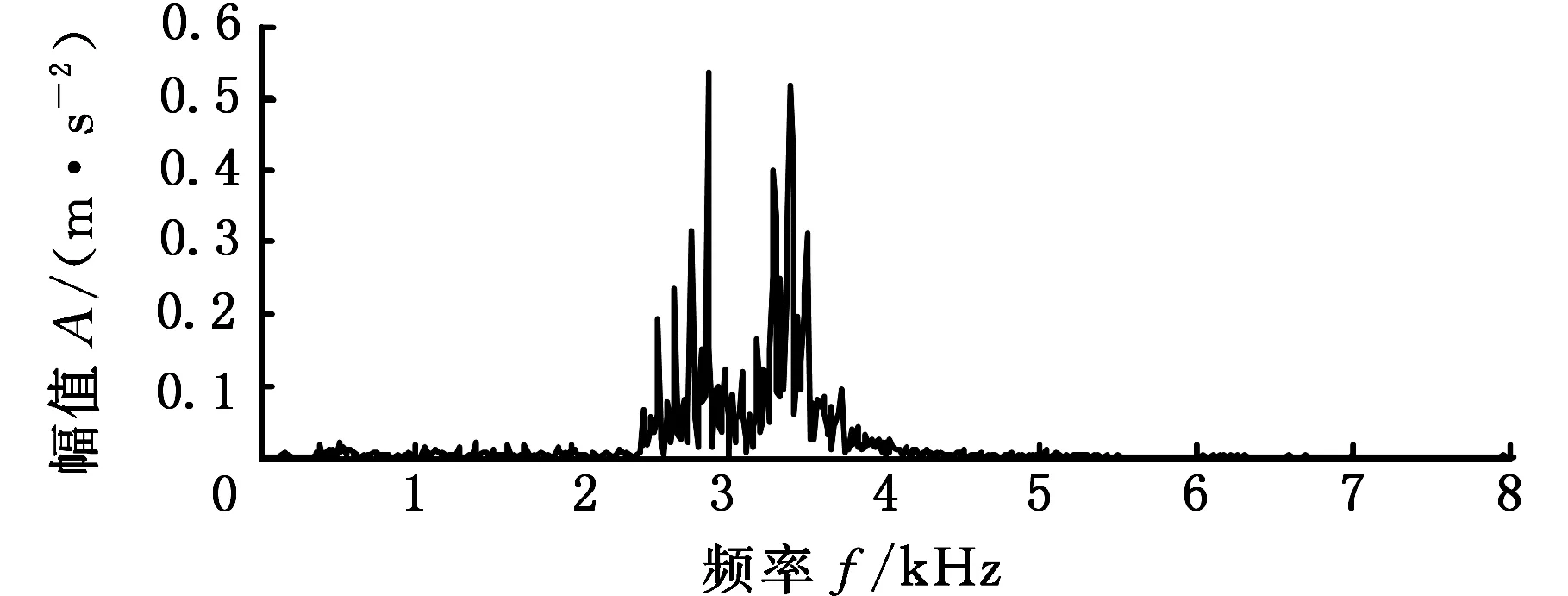
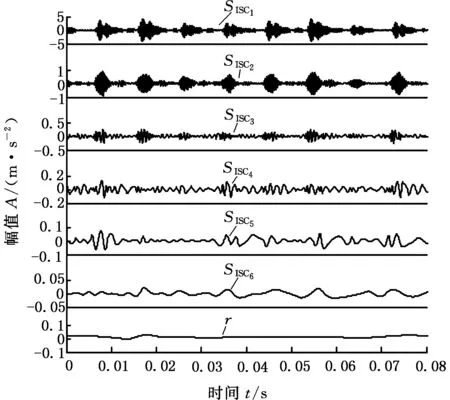
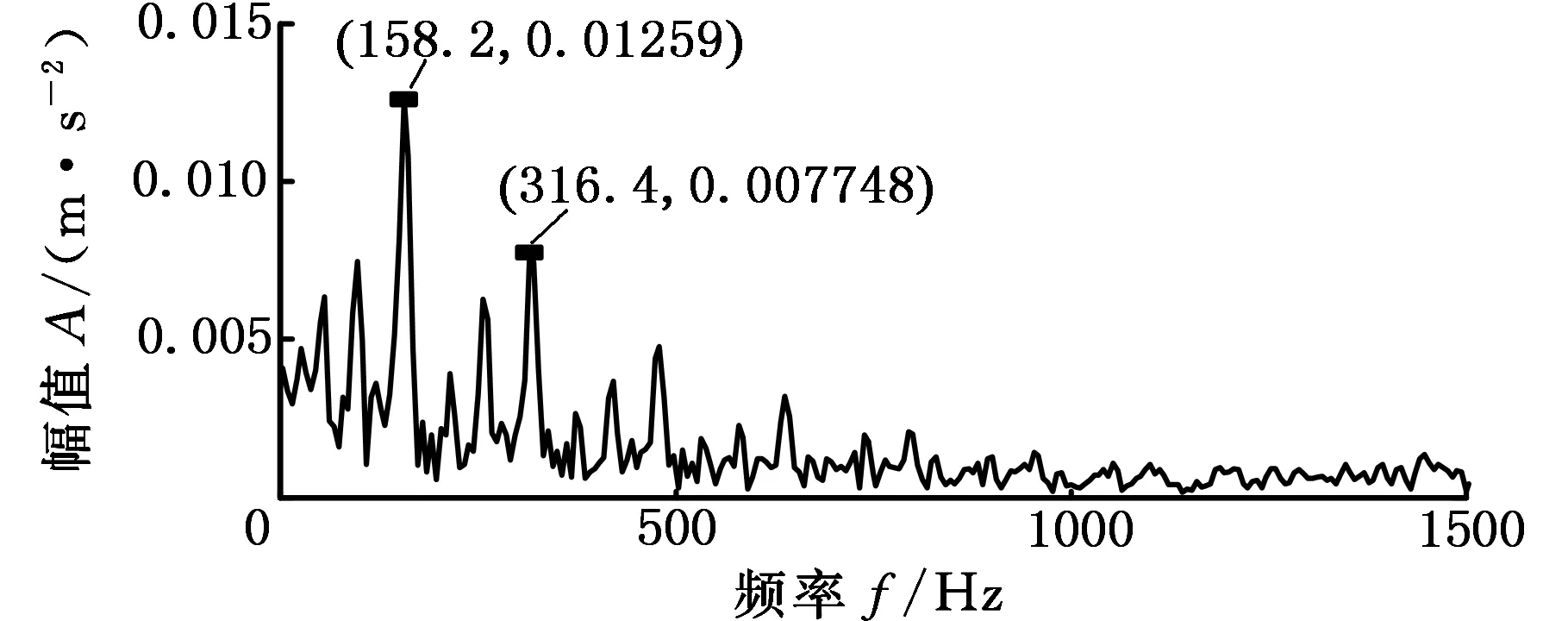
数据降维是指将高维数据通过线性或非线性映射投影到低维空间来获得其低维表示。局部切空间排列是一种典型的非线性流形学习算法,其核心思想是利用样本中某个点及其邻域的切空间来表示这些数据点的局部几何性质,通过数据点在局部切空间上的投影来获得局部低维坐标,然后将这些局部低维坐标经排列变换来构造全局低维坐标[11-12]。对于一个给定的m维数据集,X={x1,x2,…,xn},xi∈Rm。为了提取出一个d维(d (1)对于高维空间的每个数据点xi,基于欧氏距离测度函数确定出由k个邻近点组成的邻域xi=(xi1,xi2,xi3,…,xik)。 (2)在xi的邻域内选择一组正交基Qi构成xi的d维切空间,计算邻域内每个点xij(j=1,2,…,k)的切空间的正交投影: (4)由于e是矩阵B的0特征值对应的特征向量,所以取B的第2~d+1个最小特征值对应的特征向量所组成的矩阵就是X中的正交低维全局坐标映射向量Ti,i=1,2,3。 故障特征频率提取方法 基于LCD和LTSA维数约减的故障特征频率提取方法的具体步骤如下[13-14]: (1)采用LCD方法对原始振动信号x进行分解,得到若干个ISC分量,每个分量都包含了一定程度的故障特征信息。 (2)将所得到的n个ISC分量组成n维特征向量X,记为 X=(SISC1,SISC2,…,SISCi)i=1,2,…,n 采用局部切空间排列方法(LTSA)对X进行降维处理,得到m(m T=(k1,k2,…,kj)j=1,2,…,m (3)对得到的m维特征向量(k1,k2,…,km)进行信号重构,得到新的信号y,y包含了振动信号中的主要故障特征。相比原始信号,滤除掉了背景噪声和一些次要特征,简化了原始信号所含信息,增强了故障信息。 (4)对重构信号进行频谱分析,提取信号中的故障特征频率。 为了验证本文所提出的故障特征频率提取方法的有效性,采用滚动轴承外圈、内圈和滚动体故障振动信号进行分析。试验数据来源于美国西储大学滚动轴承故障模拟试验台。试验中所采用的轴承为6205-2RSJEMSKF深沟球轴承,轴承节径为39.04mm,滚动体直径为7.94mm,滚动体个数为9,接触角为0,转频约为29Hz。轴承故障为使用电火花加工技术在轴承的内圈、外圈、滚动体上布置的单点故障,故障点的故障直径为0.1778mm,损伤深度为0.28mm,轴承转速为1772r/min,采用加速度传感器采集振动信号。振动信号的采样频率为48kHz,数据长度为48 000个点。根据SKF6205 深沟球轴承的标准参数,通过轴承故障频率计算公式可得到内外圈两种故障的故障频率,如表1所示。图1为故障轴承故障特征频率提取步骤。 表1 滚动轴承故障频率Tab.1 Failure frequency of rolling bearing 图1 滚动轴承故障频率提取流程Fig.1 Failure frequency extract steps of rolling bearing 首先以轴承外圈故障信号为例进行验证,从一组故障信号中任意选取时长为0.08 s的振动信号进行分析,图2和图3分别为该段滚动轴承外圈故障振动信号的时域波形和频域波形,由于背景噪声干扰及信号的非线性、非平稳性,很难从时域波形和频域波形上观察到轴承外圈的故障信息,在频谱图上的0~2000 Hz区间无法直接提取到故障特征频率。 图2 滚动轴承外圈故障时域波形Fig.2 Time domain waveform of outer ring fault 图3 滚动轴承外圈故障频域波形Fig.3 Frequency domain waveform of outer ring fault 对滚动轴承外圈振动信号进行LCD分解,得到如图4所示的高频到低频的6个ISC分量和一个残余分量r。选取6个ISC分量组成6维特征向量,采用LTSA方法对6维特征向量进行降维,目标维数为3,邻域参数k=12,通过计算得到3维特征向量,对3维特征向量进行信号重构得到如图5所示的重构信号,相比原始的时域信号,重构信号在一定程度上增强了信号的周期性信息。对重构信号进行频谱分析,得到图6所示的0~2000 Hz范围内的重构信号频域波形图。从频域图上可以非常清晰地看到105.5 Hz及其二倍频、三倍频,基本没有干扰噪声,并且与理论计算得到的外圈故障特征频率105 Hz非常接近,可以认为105.5 Hz为实际得到的轴承外圈的故障特征频率。 图4 轴承外圈故障振动信号LCD分解结果Fig.4 LCD decomposition results of bearing outer ring fault 图5 LTSA降维后的重构信号Fig.5 Reconstruct signal of LTSA Dimension reduction 图6 重构信号频域波形图Fig.6 Frequency domain waveform of reconstruct signal 通过以上分析过程可知,采用LTSA降维的方法对LCD分解得到的信号进行重构,然后分析其频谱特性可以非常有效地提取到轴承外圈故障特征频率。这种方法有两个优点:一是避免了振动信号经LCD分解后选取合适ISC分量的不便;二是采用LTSA流形学习算法,通过数学的方法有效地挖掘高维数据中的低维特征,降低信号的无规则复杂度,增强了有规律的故障特征。对轴承外圈故障信号的分析过程也较为充分地说明了这两个优点。 为进一步验证该方法在微弱故障特征频率提取中的有效性,采用轴承内圈故障振动信号进行分析,内圈故障相对于外圈故障较为微弱。图7为轴承内圈故障信号的时域波形图,图8为信号的频域波形图,图9为采用本文所述方法得到的重构信号的0~1500 Hz范围内的频谱图,从图9中同样可以清晰地看到内圈故障的特征频率158.2 Hz及其倍频成分,该方法对于轴承内圈故障信号同样有效。因此,该方法对微弱故障信号的特征频率提取具有一定效果。 图7 滚动轴承内圈故障时域波形Fig.7 Time domain waveform of inner ring fault 图8 滚动轴承内圈故障频域波形Fig.8 Frequency domain waveform of inner ring fault 图9 重构信号频域波形图Fig.9 Frequency domain waveform of reconstruct signal 本文提出了一种新的故障特征频率提取方法,该方法结合了LCD分解方法和LTSA流形学习算法。LCD分解可以将振动信号分解为不同尺度下的多个ISC分量,LTSA方法可以有效地挖掘ISC分量所含信息的主要特征并得到重构信号,对重构信号进行频谱分析可得到故障特征频率。对滚动轴承内圈和外圈故障振动信号的分析验证了所提出方法的有效性,该方法对微弱故障振动信号的故障特征频率的提取也有一定的效果。 [1] 田野,侯跃谦,李萌,等.基于小波减噪的滚动轴承故障频率的识别[J].煤矿机械,2005(6):141-142. TIAN Ye, HOU Yueqian, LI Meng, et al. Fault Frequency Recognition of Rolling Bearing Based on Wavelet[J].Journal of Coal Mine Machinery,2005(6):141-142. [2] 关羽,郭永刚,水小平,等. 基于小波包变换的二滩大坝地震响应能量分析[J]. 振动、测试与诊断,2014,34(6),1159-1163. GUAN Yu, GUO Yonggang, SHUI Xiaoping, et al. Energy Analysis of Ertan Dam Seismic Response Based on Wavelet Packet Transform[J].Journal of Vibration, Measurement&Diagnosis,2014,34(6),1159-1163. [3] 程军圣,郑近德,杨宇.基于局部特征尺度分解的经验包络解调方法及其在机械故障诊断中的应用[J]. 机械工程学报,2012,48(19):87-94. CHENG Junsheng, ZHENG Jinde, YANG Yu. Empirical Envelope Demodulation Approach Based on Local Characteristic-scale Decomposition and Its applications to Mechanical Fault Diagnosis[J].Journal of Mechanical Engineering, 2012,48(19):87-94. [4] 程军圣,郑近德,杨宇.一种新的非平稳信号分析方法——局部特征尺度分解法[J].振动工程学报,2012,25(2):215-220. CHENG Junsheng, ZHENG Jinde, YANG Yu. A Nonstationary Signal Analysis Approach—the Local Characteristic-scale Decomposition Method[J].Journal of Vibration Engineering, 2012,25(2):215-220. [5] 杨宇, 曾鸣, 程军圣. 一种新的时频分析方法——局部特征尺度分解[J]. 湖南大学学报(自然科学版), 2012, 39(6): 35-39. YANG Yu, ZENG Ming, CHENG Junsheng. A New Time-frequency Analysis Method—The Local Characteristic Scale Decomposition[J]. Journal of Hunan University(Natural Sciences),2012,39(6):35-39. [6] 杨宇,潘海洋,程军圣.基于LCD降噪和VPMCD的滚动轴承故障诊断方法[J].中国机械工程,2013,24(24):3338-3344. YANG Yu,PAN Haiyang, CHENG Junsheng. A Rolling Bearing Fault Diagnosis Method Based on LCD Denoising and VPMCD[J].China Mechanical Engineering,2013,24(24):3338-3344. [7] 向丹, 葛爽. 基于EMD样本熵-LLTSA的故障特征提取方法[J]. 航空动力学报, 2014, 29(7): 1535-1542. XIANG Dan, GE Shuang.Method of Fault Feature Extraction Based on EMD Sample Entropy and LLTSA[J].Journal of Aerospace Power, Journal of aerospace Power , 2014, 29(7): 1535-1542. [8] 谢平, 杜义浩, 黄双峰. 基于信息熵的复杂机械系统非线性特征提取方法研究[J]. 振动与冲击, 2008, 27(7): 135-137. XIE Ping, DU Yihao, HUANG Shuangfeng.Research on Nonlinear Feature Extracting Method of Complex Mechanical System Based on Information Entropy[J]. Journal of Vibration and Shock, 2008, 27(7): 135-137. [9] 艾延廷, 付琪, 田晶. 基于融合信息熵距的转子裂纹-碰摩耦合故障诊断方法[J]. 航空动力学报, 2013, 28(10): 2161-2166. AI Yanting,FU Qi,TIAN Jing. Diagnosis Method for Crack-rubbing Coupled Fault Based on Integration of Information Entropyin Rotor System Distance[J]. Journal of Aerospace Power,2013, 28(10): 2161-2166. [10] 李鹏宇, 邵忍平, 汪亚运. 基于Shannon熵的LCD-SVM的方法在齿轮故障分类中的研究[J]. 机械传动, 2014, 38(4): 5-8. LI Pengyu, SHAO Renping, WANG Yayun. Study on the LCD-SVM Method Based on Shannon Entropy Used in Gear Fault Classification[J].Journal of Mechanical Transmission, 2014, 38(4): 5-8. [11] ZHANG T H,YANG J,ZHAO D L.Linear Local Tangent Space Alignment and Application to Face Recognition[J].Neurocomputing,2007,70:1547-1553. [12] ZHANG Z Y,ZHA H Y. Principal Manifolds and Nonlinear Dimensionality Reduction by Local Tangent Space Alignment[J].Scientific Computing,2004,26(1): 313-338. [13] 张熠卓,徐光华,梁霖.利用增量式非线性流形学习的状态监测方法[J].西安交通大学学报,2011,45(1): 64-68. ZHANU Yizhuo, XU Guanhua, LIANG Lin. Condition Monitoring Method for Mechanical Equipments Based on Incremental Nonlinear Manifold Learning[J]. Journal of Xi’an Jiaotong University, 2011,45(1):64-68. [14] 梁霖,徐光华,栗茂.冲击故障特征提取的非线性流形学习方法[J].西安交通大学学报,2009, 43(11): 95-99. LIANG Lin, XU Guanghua, LI Mao. Nonlinear Manifold Learning Method of Mechanical Impact Faults Extraction[J].Journal of Xi’an Jiaotong University, 2009,43(11):95-99. (编辑 王艳丽) Fault Frequency Extracting Methods Based on LCD and LTSA WANG Fei FANG Liqing LYU Yan Artillery Engineering Department, Ordnance Engineering College, Shijiazhuang,050003 As the fault vibration signal characteristics presented non-stationary and the fault frequencies were hard to extracted, a new feature extraction method was proposed .This approach combined LCD and LTSA which was one of the typical manifold learning methods to extracting fault frequencies. Firstly, the vibration signals were decomposed into multiple intrinsic scale components in multidimensional feature vectors using LCD. Secondly, LTSA method was applied to compress the high-dimensional vectors into low-dimensional vectors, the low-dimensional vectors were used to reconstruct and the new fault signals were obtained. Finally, the new fault signal’s spectrum were analysed and the fault characteristic frequencies were acquired. The rolling bearing fault experimental results show that this new technique may extract the inner and outer ring fault frequencies, it verifies the effectiveness of this new approach. local characteristic-scale decomposition(LCD); local tangent space alignment(LTSA); fault frequency; rolling bearing; spectral analysis 2016-04-12 河北省自然科学基金资助项目(E2016506003) TH165.3 10.3969/j.issn.1004-132X.2017.05.010 王 斐,男,1990年生。军械工程学院火炮工程系博士研究生。研究方向为兵器性能检测与故障诊断技术。发表论文5篇。E-mail:m15536259885@icloud.com。房立清,男,1969年生。军械工程学院火炮工程系教授、博士研究生导师。 吕 岩,男,1991年生。军械工程学院火炮工程系硕士研究生。

3 基于局部特征尺度分解和LTSA的
4 滚动轴承故障信号分析

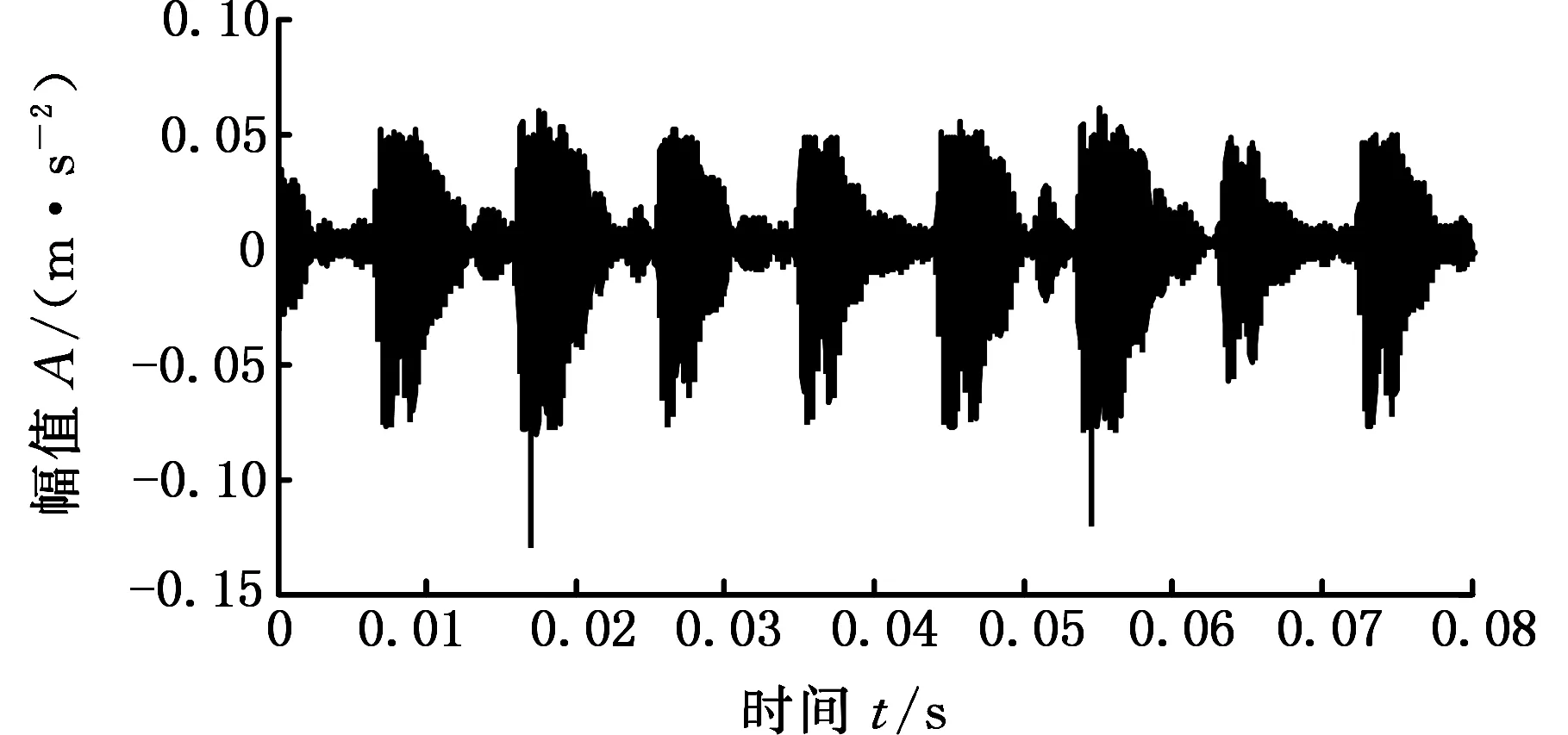
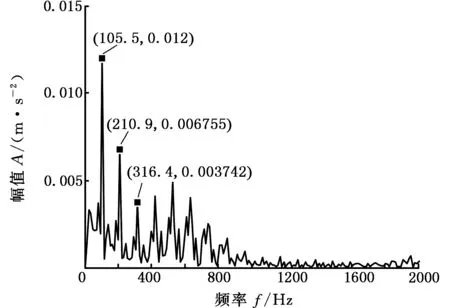
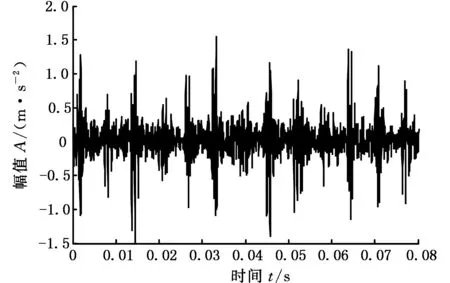
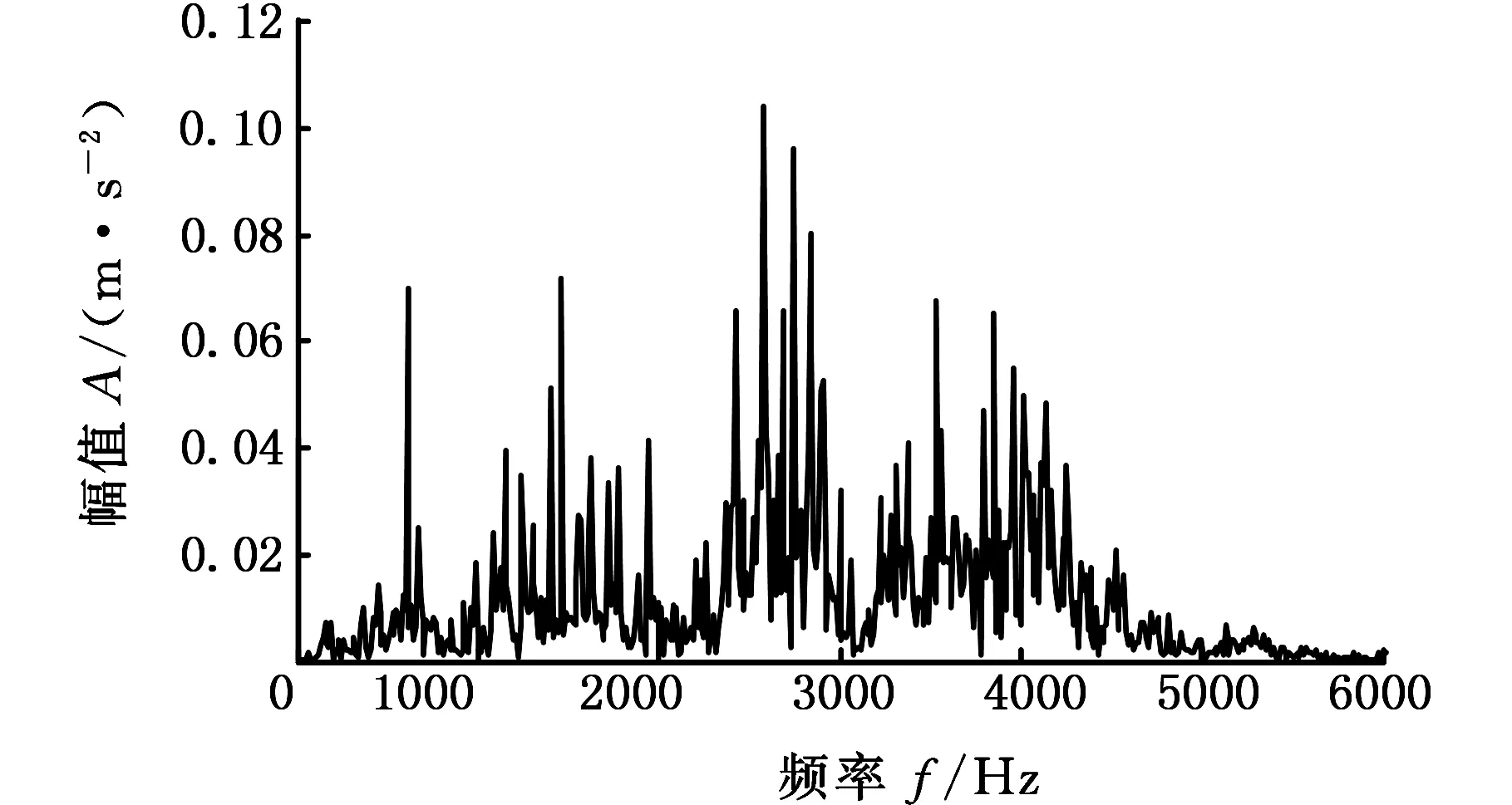
5 结语

