面向多向3D打印的混联机构及其运动分析

周 辉 丁 锐 秦友蕾 曹 毅

1.江南大学机械工程学院，无锡，2141222.江南大学江苏省食品先进制造装备技术重点实验室，无锡，214122

面向多向3D打印的混联机构及其运动分析

周 辉1, 2丁 锐1, 2秦友蕾1, 2曹 毅1, 2

1.江南大学机械工程学院，无锡，2141222.江南大学江苏省食品先进制造装备技术重点实验室，无锡，214122

为解决多向3D打印装备瓶颈问题，提出一种完全解耦五自由度混联机构作为3D打印的执行机构，该机构由并联模块3-CPaRR和串联模块RRo组成，其中并联模块由3条相同CPaRR支链构成，可实现空间的三维移动，串联模块RRo用于调整打印头姿态，改善3D打印过程中的台阶现象、干涉问题。基于约束螺旋理论，分析了3CPaRR&RRo机构自由度，并通过ADAMS建模对其进行了验证。然后运用D-H法求得混联机构的运动学方程，对机构的位姿正解表达式求导，得到了机构的雅可比矩阵和末端速度方程，分析了机构在工作空间内的奇异性问题，通过对模型运动仿真，绘制出了机构末端输出速度曲线，验证了上述分析的正确性。

多向3D打印；混联机构；完全解耦；螺旋理论；运动学

0 引言

3D打印技术(增材制造)诞生于20世纪80年代中后期[1]，它是根据三维 CAD设计数据，采用分层、叠加成形的方式逐层增加材料来生成三维实体的。3D打印在复杂结构件制造、文物修复、生物医学领域具有广阔的应用前景，是传统制造技术的有益补充[2]。目前，大部分3D打印都采用单向分层熔融沉积技术，即打印头姿态固定，沿着垂直于打印头方向运动，这种方法具有轨迹规划简单、制造速度较快、成本低等优点。但这种打印模式也存在明显的缺点：打印的产品表面质量比较差，易出现不光滑的台阶形状[3]；在有些现有零件上增加几何特征比较困难；打印的产品力学性能具有方向性。为了解决这些问题，人们提出了在打印过程中调整打印头姿态的技术，即多向3D打印(multi-direction 3D printing)技术。多向3D打印技术可以显著改善单向3D打印过程中的台阶现象、干涉问题和材料特性的方向性。

实现多向3D打印技术的关键是3D打印设备。商用的3D打印设备大多是基于三平动的串联机构，这些设备可实现单向分层3D打印。为了实现多向分层3D打印，一些具有更高自由度的3D打印设备相继出现，它们主要通过两类方法实现多向3D打印，一类是通过旋转工件平台，配合打印头的三自由度平动[4-5]；另外一类是通过增加打印头的自由度[6-9]，使其具备改变姿态的能力。但由于这些均为串联式结构，具有误差累积的特点，精度低，悬臂式结构刚度差，所以这类装备的打印质量和效率均不理想。这些缺点促使学者们开始研究开发并联式3D打印设备,出现了一些基于Delta、Stewart机构的并联式3D打印设备[10]，这些并联机构虽然可以用于多向3D打印，但存在动力学模型复杂、路径规划难、柔性差、对简单的打印任务驱动超冗余且经济性差等缺点。然而，完全解耦混联机构很好地解决了上述串并联式结构的问题，不仅具有高精度，高刚度的特征，而且控制简单。

本文基于文献[11-12]构型方法提出一种完全解耦3T2R五自由度混联机构，将其作为多向3D打印机的结构本体，同时对其运动性能进行了分析研究。

1 多向3D打印机构描述

多向3D打印机的结构本体采用一种新型3CPaRR&RRo混联机构，其中C为圆柱副、Pa为平行四边形铰链、R为转动副、RRo为两个转动副轴线交于公共点，它由并联模块3-CPaRR和串联模块RRo构成，并联模块3-CPaRR能够实现空间的三维移动，主要用以保证3D打印设备具有良好的刚性、较快的打印速度，可单独作为单向3D打印设备的执行机构，串联模块RRo用于打印过程中调整打印头姿态，改善3D打印过程中的台阶现象、干涉问题。多向3D打印机构CAD模型如图1所示。并联模块3-CPaRR由3条完全相同支链CPaRR将动平台和支架相连，每条分支都具有5个自由度，3条支链中与定平台连接的3个圆柱副，其轴线相互垂直，3D打印头通过两个交于一点的转动副和动平台连接。

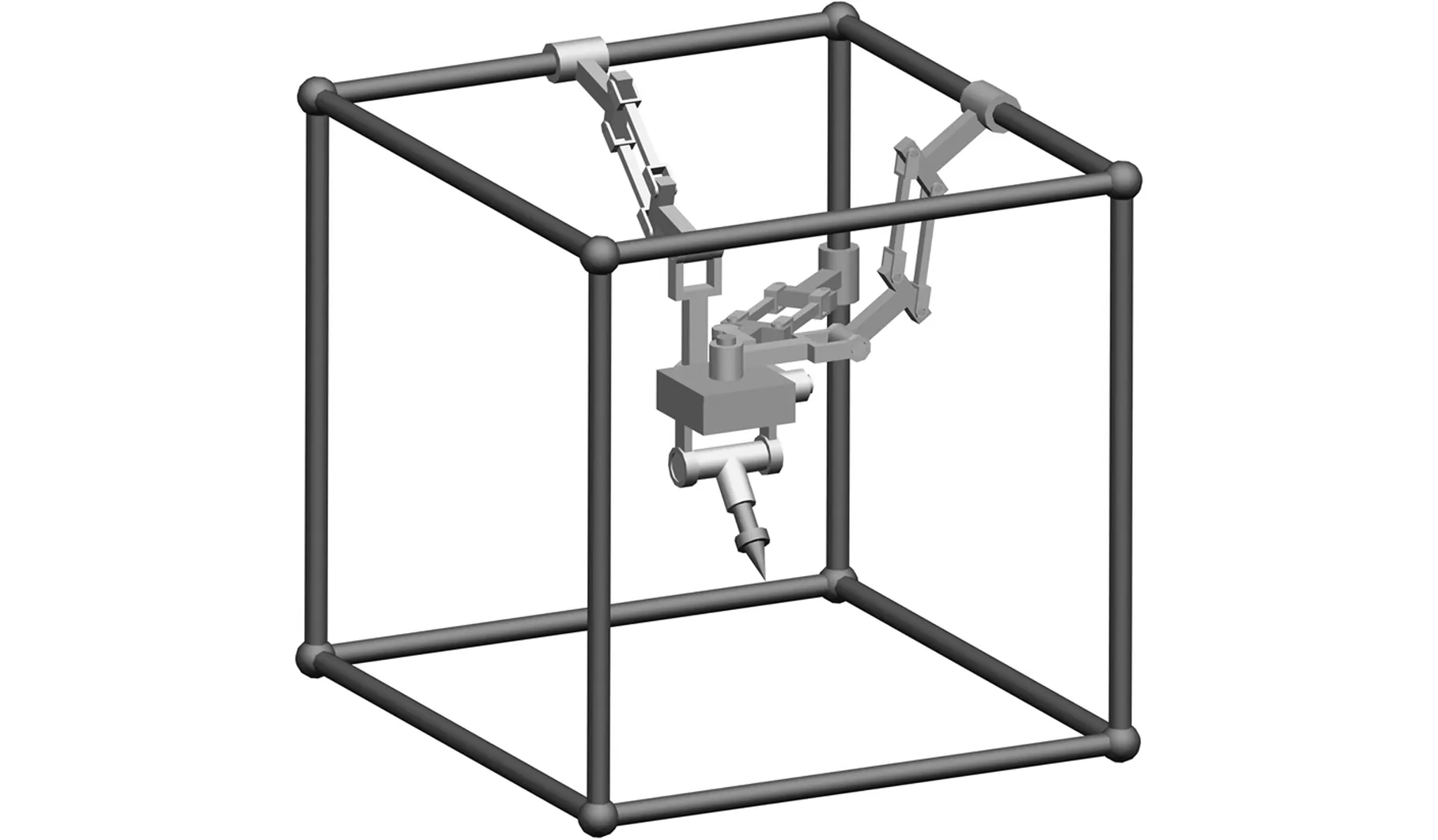
图1 多向3D打印机构CAD模型Fig.1 A CAD model of mechanism for multi-direction 3D printing

如图2所示，将每个支链的每个运动副进行编号，可以表示成第i条支链的第j个运动副，串联模块的转动副为R4、R5。3条支链中圆柱副为Ci1、平行四边形铰链为Pai2、转动副Ri3的轴线互相平行，2个转动副Ri4、Ri3的轴线垂直，与动平台连接的转动副Ri4轴线相互垂直(i=1,2,3)，3条支链的第一个圆柱副Ci1正交放置。按照图2所示，将定坐标系OXYZ设在定平台3个相互垂直的轴上,轴心为O，以第1条支链为例，则C11平行于Y轴，Pa12中4个转动轴线平行于Y轴，R13平行于Y轴。R14平行于动平面与转动副R13垂直。串联模块的转动副R4轴线平行于Y轴，转动副R4、R5轴线垂直并且两个轴线交于一点。

图2 3CPaRR&RRo混联机构Fig.2 A 3CPaRR&RRo hybrid mechanism

2 混联机构的约束分析

2.1 混联机构3CPaRR&RRo的自由度分析

运用修正的Grübler-Kutzbach通用自由度计算公式[13]：

(1)

式中,M为机构的自由度；d为机构的阶数；n为包括机架的构件数目；g为运动副的数；fi为第i个运动副的自由度；μ为过约束数；ζ为局部自由度。

将3CPaRR&RRo混联机构导入到ADAMS中的Model Verify模块验证上述机构自由度，经验证机构自由度数为5。

对于混联机构中的并联模块，如图2所示$ij为第i条支链的第j个运动副的运动螺旋。3CPaRR并联机构中的Pa平行四边形铰链可用一个等效广义移动副替代，则支链可认为由4个运动副CPRR组成。并联机构的等效支链一的运动螺旋系为

(2)

其中，d12、f12、d13、f13、e14、f14为非零实数。

由式(2)运动螺旋可得约束螺旋系为

(3)

支链二的运动螺旋系为

(4)

其中，d22、e22、d23、e23、d24、f24为非零实数。

由式(4)运动螺旋可得约束螺旋系为

(5)

支链三的运动螺旋系为

(6)

其中，e32、f32、e33、f33、d34、e34为非零实数。

由式(6)运动螺旋可得约束螺旋系为

(7)

并联机构3CPaRR约束螺旋系为

(8)

式(8)表明，3条支链对动平台作用了3个力偶。这3个力偶彼此线性无关，刚好限制了动平台上的3个转动，所以此并联模块可以实现空间三维移动，再加上串接在动平台上的两个转动，此混联机构具有三移两转五个自由度。

2.2 机构输入运动副选择

选取与定平台相连的三个在空间相互垂直的圆柱副的移动特征为输入，对于串联模块的RRo驱动副分别是R4、R5。根据螺旋理论的并联机构驱动选取方法，如果输入运动选取正确，当输入运动副被约束时，则动平台的约束螺旋系的最大线性无关数为6[14]。此时，限制这三个圆柱副移动特征后，对每条支链的运动螺旋分别求其反螺旋，可得到动平台的约束螺旋系为

(9)

显然式(9)中约束螺旋矩阵的秩是6，此时的动平台自由度是0。将3CPaRR&RRo混联机构导入到ADAMS中的Model Verify模块，设定3个圆柱副以及与机构末端连接的两个转动副RRo为5个驱动副，5个驱动副驱动时其机构的自由度为0，故输入运动副选取正确。

2.3 消极运动副判定

设固定在动平台上的点F的角速度矢量为ωn，线速度矢量为vn，则动平台的运动螺旋为

(10)

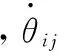
将支链1的运动螺旋系代入式(10)中，可得

(11)

由于并联模块只能三维移动，所以ωn=(0，0，0)T，代入式(11)中可得

(12)

由此可以看出支链1的转动副R14的转动速度为0。同理可知，支链2与支链3的转动副R24、R34的转动速度为0。因此并联模块各支链与动平台连接的转动副在机构发生运动时均不发生转动,是个消极的运动副。并联机构3CPaRR可以简化为完全对称的3-CPaR机构。

3 多向3D打印机构的运动学分析

3.1 并联模块位置分析

如图3所示，将定坐标系OXYZ设在定平台上，动坐标系fxyz设置在动平台的几何中心上，动平台长为lx，宽为ly。支链一中圆柱副C11的起始点位于A0，距O点距离为Dx，圆柱副C11的移动输入为q1。支链二中起始点距O点距离为Dy，圆柱副C21的移动输入为q2。支链三中起始点距O点距离为Dz，圆柱副C31的移动输入为q3。设支链一中第一个零件AB的长度为a，平行四边形铰链中构件BC的长度为b，零件CD的长度为c，连杆DE的距离为d，E点距离动平台中心点f的距离为h，由于机构具有三条相同的支链，故支链二、支链三具有与支链一相同的参数，三条支链中，圆柱副C11、C21与平面OXY所成

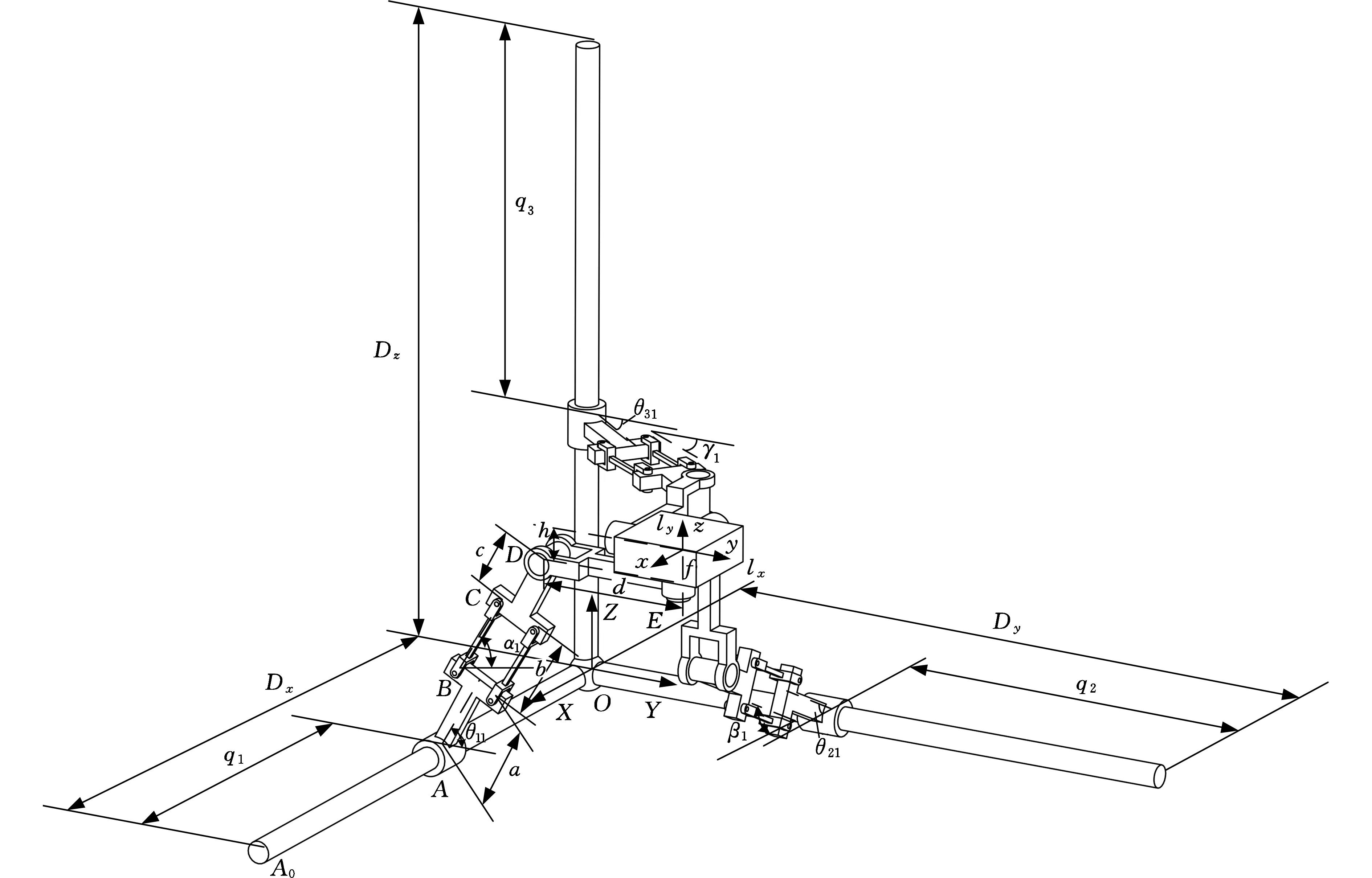
图3 3CPaRR并联模块运动参数Fig.3 Kinematic parameters of 3CPaRR parallel mechanism

角度分别为θ11、θ21，平行四边形铰链Pa12、Pa22与平面OXY所成角度分别为α1、β1，圆柱副C31轴线和平行四边形铰链Pa32与平面OYZ所成角度分别为θ31、γ1。

根据图5的几何关系，可得动平台中心点f的坐标。对于第一条支链:

f=(Dx-q1，acosθ11+(b+c)cosα1+
d，asinθ11+(b+c)sinα1+h)

(13)

对于第二条支链:

f=(acosθ21+(b+c)cosβ1+0.5lx，Dy-q2，
asinθ21+(b+c)sinβ1+d)

(14)

对于第三条支链:

f=(asinθ31+(b+c)sinγ1+d，acosθ31+
(b+c)cosγ1+0.5ly，Dz-q3)

(15)

由式(13)～式(15)可得

(16)

由此可以得到3CPaRR机构的运动学正解为

(17)

由式(13)可以得到运动学的逆解为

(18)

3.2 串联模块位置分析

串联机构位置分析通常基于D-H方法[15]，该方法通过建立D-H参数来描述连杆间的相对关系，并将其用矩阵表示，通过连杆矩阵复合变换求解出末端的变换矩阵，建立运动方程[16]。

如图4所示，建立各连杆的坐标系，对应的D-H参数如表1所示。

图4 串联模块坐标系分布Fig.4 Coordinate system of modules in series

关节iαi-1(°)ai-1(mm)di(mm)θi(°)29000θ23-9000θ3

将D-H坐标参数代入式(18)可以求解出连杆的齐次变换矩阵为

机构末端相对于坐标系1的变换矩阵为

(19)

坐标系1相对于动平台的变换矩阵为

(20)

那么机构末端相对于并联模块动平台的变换矩阵，也即串联机构正运动学方程为

(21)

3.3 混联机构位置分析

(22)

(x0,y0,z0)为并联机构动平台上点f相对于静坐标系坐标原点O的位置。T为3CPaRR&RRo混联机构的运动学正解。所以

则此混联机构的位置方程为

(23)

把式(16)代入式(23)中可以得到

(24)

(25)

式中,sα=sinα，cα=cosα，sβ=sinβ，cβ=cosβ，sγ=sinγ，cγ=cosγ。

将欧拉角公式和机构的姿态方程对应起来，可以得到：

(26)

由式(26)可以得到混联机构姿态ɑ、β、γ的正解为

(27)

4 混联机构速度分析

混联机构的速度为机构位置对时间的一阶导数，故对式(23)求导可得末端执行器的线速度为

(28)

混联机构的角速度为机构的姿态对时间的一阶导数，故对式(27)求导可得末端执行器的角速度为

(29)

由式(25)可得

(30)

(31)

则机构的雅可比矩阵为

(32)

观察发现式(32)为一个5×5的对角矩阵，由完全解耦定义可知当速度雅可比矩阵为对角阵时，混联机构的运动具有完全解耦性。

五自由度3CPaRR&RRo混联机构的奇异问题可以通过J矩阵的秩进行分析判断[15]。由于此雅可比矩阵为一个5×5对角阵，故可以确定该多向3D打印机构在工作空间内不存在奇异位形。

5 多向3D打印机构的运动学仿真

为了能更加直观地反映所提出机构为完全解耦混联机构，以及证明上述理论分析的正确性，对图1所示的机构在ADAMS软件中进行速度仿真。设机构并联单元中的3个驱动副C11、C21、C31的输入线位移方程分别为：q1=8×10-3sin2πt，q2=6×10-3sin4πt，q3=-4×10-3sin8πt(0≤t≤1 s)。

将上述输入位移方程代入式(28)中，可得到3D打印机构的输出速度方程，即v1=-1.6×10-2πcos2πt，v2=-2.4×10-2πcos4πt，v3=-3.2×10-2cos8πt(0≤t≤1 s)，图5给出了机构末端点的线速度仿真曲线，不难看出理论推导出的线速度v1、v2、v3与vx、vy、vz线速度仿真曲线相一致。

图5 末端输出线速度仿真曲线Fig.5 Simulation curves of linear velocity of the end-effector

设串联单元的两个驱动副的输入角位移方程分别为θ2=0.4sin2πt，θ3=0.2sin2πt，分别将2个输入方程代入式(29)可得出驱动副的输入角速度方程ω2=-0.8πcos2πt，ω3=0.4πcos2πt(0≤t≤1 s)。角速度ωy、ωz仿真曲线如图6所示，此结果与推导出的输入角速度方程ω2、ω3结果相同。

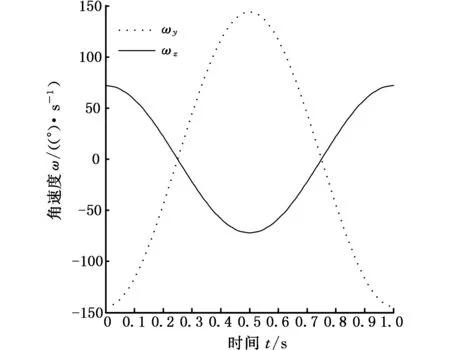
图6 末端输出角速度仿真曲线Fig.6 Simulation curves of angular velocity of the end-effector

上述理论分析以及运动仿真结果表明3CPaRR&RRo混联机构能够实现三维移动输入与输出的一一对应关系，同时该机构末端还可以绕Y轴、Z轴转动，用以调节机构运动的姿态，具有精度高、运动完全解耦的优点，因此可作为多向3D打印机的执行机构。

6 结论

(1) 3CPaRR&RRo混联机构采用了3条完全相同支链正交布置的并联单元串接一个两自由度的转动头，基于旋量理论，分析了3CPaRR&RRo混联机构末端输出为三移两转五自由度的运动，通过ADAMS中Model Verify模块得以验证。

(2) 3CPaRR&RRo混联机构的驱动简单，并联模块采用三个移动副，串联模块采用两个转动副。基于D-H法求解了机构运动学方程，推导了机构位置和姿态的正解，对其求导得到了机构速度表达式。

(3) 利用运动影响系数求得3CPaRR&RRo混联机构速度雅可比矩阵，理论验证了机构的解耦性，并分析了机构在工作空间的奇异问题。最后通过对机构运动仿真，证明了理论分析的正确性。

[1] GIBSON I, ROSEN D W, STUCKER B. Additive Manufacturing Technologies [M]. New York: Springer, 2010:54-61.

[2] 中国机械工程学会. 3D打印，打印未来[M]. 北京：中国科学技术出版社，2013: 20-35. Chinese Mechanical Engineering Society. 3D Printing, print the future[M]. Beijing: China Science and Technology Press, 2013: 20-35.

[3] ONUH S O, HON K K B. Optimising Build Parameters for Improved Surface Finish in Stereo Lithography[J]. International Journal of Machine Tools & Manufacture, 1998, 38(4):329-342.

[4] JING S K, SONG G H, LIU J H, et al. A Review of Product Design for Additive Manufacturing[J]. Applied Mechanics & Materials, 2014, 635/637:97-100.

[5] PINKERTON A J, WANG W, LI L. Component Repair Using Laser Direct Metal Deposition[J]. Journal of Engineering Manufacture, 2008, 222(7):827-836.

[6] DUTTA B, PALANISWAMY S, CHOI J, et al. Additive Manufacturing by Direct Metal Deposition[J]. Advanced Materials & Processes, 2011, 169(5):33-36.

[7] CHEN Y, ZHOU C, LAO J. A Layerless Additive Manufacturing Process Based on CNC Accumulation[J]. Rapid Prototyping Journal, 2011, 17(3):218-227.

[8] LEE W C, WEI C C, CHUNG S C. Development of a Hybrid Rapid Prototyping System Using Low-cost Fused Deposition Modeling and Five-axis Machining[J]. Journal of Materials Processing Technology, 2014, 214(11): 2366-2374.

[9] CHEN Y，ZHOU C，LAO J. A Layer Less Additive Manufacturing Process Based on CNC Accumulation[J]. Rapid Prototyping Journal，2011，17(3): 218-227.

[10] SONG X，PAN Y，CHEN Y. Development of a Low-cost Parallel Kinematic Machine for Multidirectional Additive Manufacturing[J]. Journal of Manufacturing Science and Engineering，2015，137(2): 297-310.

[11] 曹毅, 秦友蕾, 陈海,等. 基于GF集理论的五自由度混联机器人构型综合[J]. 农业机械学报, 2015, 46(11):392-398. CAO Yi, QIN Youlei, CHEN Hai, et al. Structural Synthesis of 5-DOF Hybrid Mechanisms Based onGFSet[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(11):392-398.

[12] 秦友蕾, 曹毅, 陈海, 等. 两移动三转动完全解耦混联机器人机构型综合[J]. 西安交通大学学报, 2016,50(1):92-99. QIN Youlei, CAO Yi, CHEN Hai, et al. Structural Synthesis of Fully-decoupled Two-translational and Three-rotational Hybrid Robotic Manipulators[J]. Journal of Xi’an Jiaotong University, 2016,50(1):92-99.

[13] HUANG Z, LIU J F, ZENG D X. A General Methodology for Mobility Analysis of Mechanisms Based on Constraint Screw Theory[J]. Science in China, 2009, 52(5):1337-1347.

[14] 赵铁石, 黄真. 欠秩空间并联机器人输入选取的理论与应用[J]. 机械工程学报, 2000, 36(10):81-85. ZHAO Tieshi, HUANG Zhen. Theory and Application of Selecting Actuating Components of Spatial Parallel Mechanisms[J]. Chinese Journal of Mechanical Engineering, 2000, 36(10):81-85.

[15] 于靖军, 刘辛军, 丁希仑. 机器人机构学的数学基础[M]. 北京：机械工业出版社, 2009:82-86. YU Jingjun, LIU Xinjun, DING Xilun. Mathematic Foundation of Mechanisms and Robotics[M]. Beijing: China Machine Press, 2009:82-86.

[16] 李菊，赵德安，沈惠平,等. 多喷枪协同式喷涂五轴混联机器人设计[J]. 农业机械学报，2012，43(4): 216-220. LI Ju, ZHAO De’an, SHEN Huiping et al. Design of 5-axes Hybrid Robot with Several Spray Guns for Collaborative Spraying[J]. Transactions of the Chinese Society for Agricultural Machinery, 2012，43(4):216-220.

(编辑 王艳丽)

Hybrid Kinematics Mechanisms and Its Kinematic Analysis Oriented to Multi 3D Printing

ZHOU Hui1, 2DING Rui1, 2QIN Youlei1, 2CAO Yi1, 2

1.School of Mechanical Engineering, Jiangnan University, Wuxi, Jiangsu, 214122 2.The Key Laboratory for Advanced Food Manufacturing Equipment Technology of Jiangsu Province,Jiangnan University, Wuxi, Jiangsu, 214122

In order to solve the bottleneck problems of multi 3D printing equipment, a fully-decoupled five degree of freedom (5-DOF) HKM was presented as the actuator of 3D printing. HKM consisted of 3-CPaRR parallel module and RRoserial module, and the parallel module consisted of three identical CPaRR limb chains, it might realize three-dimensional translations, the serial module RRowas used to adjust the print head posture, improve 3D printing process step phenomenon and interference problems. Screw theory was applied to analyze the kinematic characteristics of mechanisms and to calculate the degrees of freedom of 3CPaRR&RRowhich were verified via the ADAMS software. The kinematic matrix of the hybrid mechanisms was carried out by using the D-H convention. The expression of the forward kinematics was deduced to obtain the Jacobian matrix and velocity equations, and the analysis of singularity was carried out. Moreover, simulation model was built with ADAMS, the velocities of the end-effectors of mechanisms were drawn. Thus, the validity of the theoretical analyses was proved.

multi 3D printing; hybrid kinematics mechanism(HKM); fully decoupled; screw theory; kinematics

2016-04-19

国家自然科学基金资助项目(50905075);江苏省六大人才高峰项目(ZBZZ-012);机械系统与振动国家重点实验室开放课题资助项目(MSV201407)

TH112

10.3969/j.issn.1004-132X.2017.05.001

周 辉，女，1973年生。江南大学机械工程学院讲师。主要研究方向为机器人技术。发表论文30余篇。丁 锐，男，1992年生。江南大学机械工程学院硕士研究生。秦友蕾，男，1991年生。江南大学机械工程学院硕士研究生。曹 毅(通信作者)，男，1974年生。江南大学机械工程学院教授。E-mail:caoyi@jiangnan.edu.cn。