液压缸非线性刚度约束系统的混沌预测及控制

刘 彬 李 鹏 刘 飞 刘浩然 姜甲浩

1.燕山大学电气工程学院，秦皇岛，0660042.燕山大学信息科学与工程学院，秦皇岛,066004

液压缸非线性刚度约束系统的混沌预测及控制

刘 彬1李 鹏1刘 飞2刘浩然2姜甲浩1

1.燕山大学电气工程学院，秦皇岛，0660042.燕山大学信息科学与工程学院，秦皇岛,066004

针对液压缸非线性刚度约束系统的混沌问题，建立了一种液压缸非线性刚度约束系统的动力学控制模型，通过Melnikov方法得到了液压缸非线性刚度约束系统发生Smale马蹄变换意义下混沌的临界条件。通过仿真分析发现，当线性控制参数发生变化时，系统发生混沌的临界条件也会发生变化，同时当线性控制参数增大时，系统的稳定性会得到提高。

液压缸；约束系统；Melnikov方法；混沌；控制

0 引言

在实际液压系统中，整个系统所有的元部件都具有非线性，只是所呈现的程度略有不同，因此理想的线性系统是不存在的。在液压系统中，含有许多非线性因素,例如阀的静态特性、死区、饱和、非线性增益、齿隙和摩擦等，所以液压系统是一个非线性动力学系统，其运行过程中因油液的可压缩性而形成的动态液压刚度、液压刚度的非线性会使运动过程中系统的固有频率不恒定，响应稳定区域变得复杂，从而影响系统的稳定运行[1-2]。

国内外学者对液压系统动态特性的研究所依据的理论多是经典控制理论和线性动力学理论。其中，SEO等[3]采用反馈线性化控制液压传动系统，替代真实系统中非线性因素，同时改善了PID控制的精度和瞬态响应。傅晓云等[4]以某水下航行器舵机液压伺服系统为研究对象，通过简化建立了舵机液压系统的线性化模型，对该液压伺服系统的动态响应特性、抗干扰能力进行了仿真分析。文献[5-7]以控制阀为研究对象，从单一元件的角度分析问题，探索了因控制阀相关参数的改变而引起的自激振动、分岔和混沌等非线性动力学行为[5-7]。王林鸿等[8-9]用混沌理论中的相空间重构、关联维数和最大Lyapunov指数等非线性动力学研究方法，对貌似随机的液压缸运行的动态时间序列信号进行分析，揭示了其混沌振动特征。

本文以液压缸非线性刚度约束作用下的系统为研究对象，建立了一种液压缸非线性刚度约束系统的动力学控制模型，着重研究了液压缸非线性刚度约束系统的混沌预测，同时引入线性控制参数，分析了线性控制参数对系统稳定性的影响。

1 液压缸非线性弹簧力

本文主要考虑一类双作用单活塞液压缸非线性刚度约束系统的振动特性，该种液压缸只在活塞的一侧装有活塞杆，因而两腔的有效面积不同，往返的运动速度和作用力也不相等，液压缸活塞运动改变了两腔液体的有效长度，引起了液压油的刚度变化。由于活塞杆的弹性模量是液压油弹性模量的近百倍，故可将活塞杆视为刚体，液压缸等效刚度主要表现为液压油的刚度。其变化规律为[8]

(1)

式中,a、b为液压缸的工况参数；L为液压缸的有效行程；βe为液压油的体积模量；Ai为液压缸活塞两侧的有效面积，i=1,2；L1为无杆腔的初始有效长度；x为系统颤振位移，为量纲一的量；Vil为阀与缸某一侧之间液压管路中液压油的体积，i=1,2。

以式(1)所示的液压缸动态刚度模型为例，对其在原点(液压缸处于未工作状态时活塞的位置，即活塞的初始位置)处进行泰勒级数展开：

(2)

式中，k1为无杆腔的等效刚度；k2为有杆腔的等效刚度。

弹簧弹性势能U具有对称性，可以表示为

(3)

则弹簧力可以表示为

(4)

弹簧力F1(x)可以表示为

F1(x)=κ1x+κ2x3

(5)

2 约束系统的动力学线性控制模型

考虑一类液压缸非线性刚度约束作用，建立一类液压缸非线性刚度约束作用下的系统动力学控制模型，如图1所示，其中，m为系统的等效质量，c为系统的线性阻尼系数，k为系统的线性刚度系数，k(x)为液压缸的非线性刚度，F为外激励幅值，ηα为引入系统的控制输入量，常数η为控制器输入方向，α为控制器参数。根据广义Lagrange原理，可以列出液压缸非线性刚度约束系统量纲一动力学平衡方程如下：

(6)

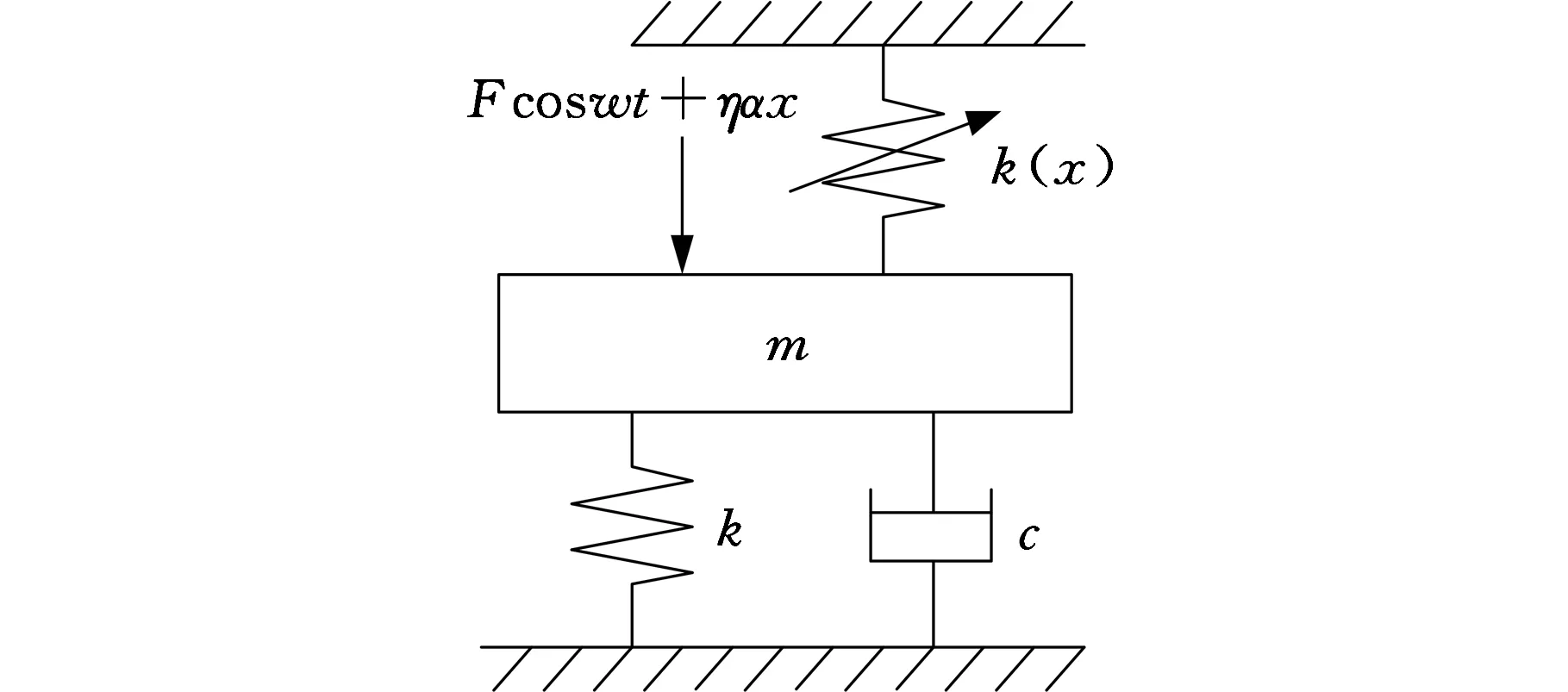
图1 系统动力学控制模型Fig.1 The dynamic control model of the system

图1所示模型中考虑一类双作用单活塞液压缸非线性刚度k(x)的约束作用，同时系统加入线性控制输入量ηα对系统进行反馈控制。

3 非线性刚度约束系统的稳定性分析

为便于计算，将系统动力学方程(式(6))简化成如下形式:

(7)

将式(7)写为状态方程形式：

(8)

其中,ε为一个小的量纲一参数。

当ε=0时，系统为一个Hamilton系统[10]，其Hamilton量为

(9)

由无阻尼未扰动方程

(10)

式(10)的微分形式为

(11)

可以得到系统的特征方程为

(12)

从而可得

(13)

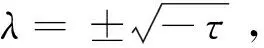
由图2可以看出：当τ<0、κ2>0时，系统有两条同宿轨，同宿轨内部的奇点是中心，同宿轨内部的轨道是包围一个中心的闭轨，而同宿轨外部的轨道是包围三个奇点的闭轨。由图3可以看出：当τ>0、κ2>0时，系统是一个单势阱的系统，系统只有一个平衡点(0，0)——中心，此时系统做稳定的周期运动，不存在Smale马蹄意义下的混沌。因此，本文以下内容主要分析当τ<0、κ2>0时系统存在Smale马蹄意义下混沌的情况。

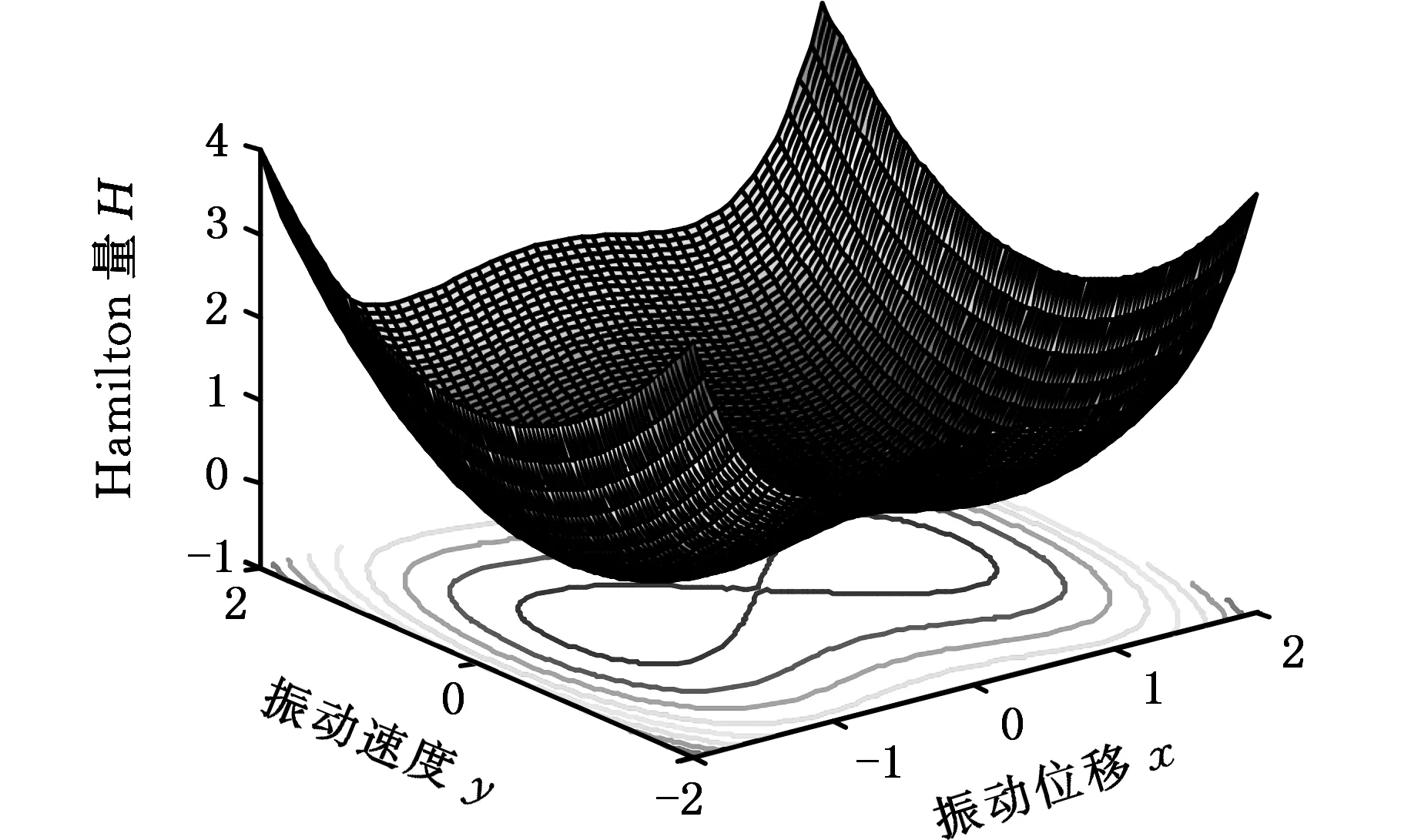
(a)势能曲面

(b)相轨迹图2 当τ<0，κ2>0时系统的势能曲面和相轨迹Fig.2 Potential energy surface and phase trajectory of the system when τ <0，κ2>0

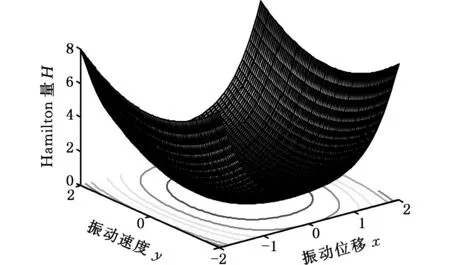
(a)势能曲面

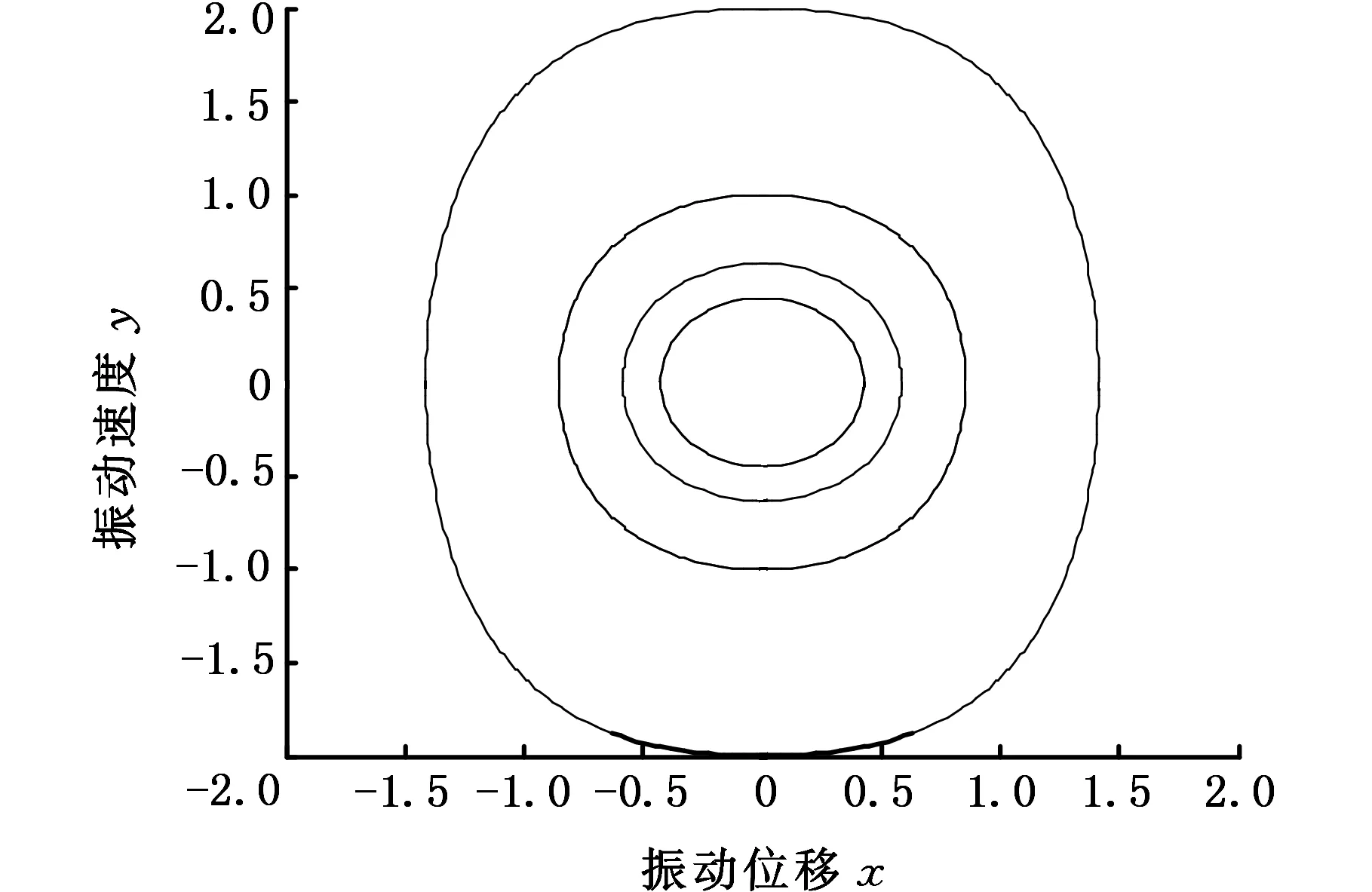
(b)相轨迹图3 当τ>0，κ2>0时系统的势能曲面和相轨迹Fig.3 Potential energy surface and phase trajectory of the system when τ>0，κ2>0

4 系统的混沌预测

(14)

所以有

(15)

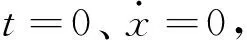
(16)

通过积分可得出两条同宿轨道关于时间的表达式：

(17)

同宿轨道对应的Melnikov函数为

(18)

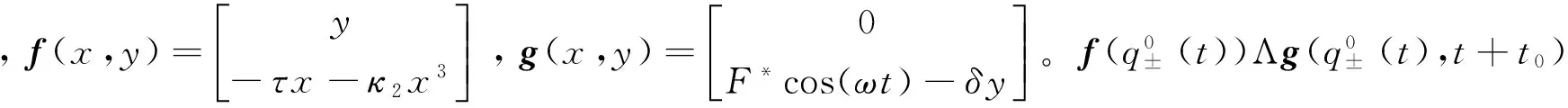
(19)

最后得到

(20)

当M(t0)=0时，可以得到

(21)

经过化简可以得到

(22)

混沌无处不在，无时不有,只是它的显现需要条件，当液压系统超出所谓的常态时，液压系统渐变或突变为混沌状态。系统由常态转变为混沌的临界值，称为系统产生混沌的临界条件。显然，当式(23)成立时，所考虑的扰动系统具有Smale马蹄变换意义下的混沌。据此可以计算出该系统发生混沌行为时的临界参数值，进而根据系统参数与系统发生混沌的临界条件关系，预测系统混沌的发生。

5 仿真分析

针对式(6)液压缸非线性刚度约束作用下系统量纲一动力学平衡方程，取仿真参数m=1、c=0.3、k=0.2、κ1=-1.2、κ2=1、ω=1.2。以下对液压缸非线性刚度约束作用下的系统混沌特性进行仿真分析。

5.1 混沌预测分析

根据式(22)所示的系统发生混沌的临界条件关系，在其他参数不变情况下，选取不同的控制输入量ρ，分析系统混沌临界条件的变化规律。按照式(22)所示的混沌预测条件可计算得到控制参数ρ取不同值时的混沌发生条件，如表1所示。

表1 不同控制参数下的混沌条件Tab.1 Chaotic conditions under different control parameters

当选取不同控制参数ρ时，以外激励幅值F为分岔参数，通过系统的分岔图，分析不同控制参数下系统发生混沌的临界条件。

从图4～图7可以看出，当控制参数ρ=-0.4时，系统分岔行为随外激励幅值F变化而变化。随着外激励幅值F的增大，系统的分岔行为如下：周期运动→阵发性混沌→倍周期运动→混沌运动。由表1可以看出，当控制参数ρ=-0.4时，计算得到系统发生Smale马蹄变换意义下混沌的外激励幅值条件为F≥0.2527，通过将此时的系统分岔图与表1对照分析可知系统在F≥0.2527时进入混沌。

图4 ρ=-0.4时的系统分岔图Fig.4 System bifurcation diagram when ρ=-0.4

由图5可以看出，当控制参数ρ=0时，系统分岔行为随外激励幅值F的变化而变化。随着外激励幅值F的增大，系统的分岔行为如下：周期运动→阵发性混沌→倍周期运动→混沌运动→倍周期运动→混沌运动。由表1可以看出，当控制参数ρ=0时，计算得到系统发生Smale马蹄变换意义下混沌的外激励幅值条件为F≥0.3182，通过将此时的系统分岔图与表1对照分析可知系统在F≥0.3182时进入混沌。

由图6可以看出，当控制参数ρ=0.4时，系统分岔行为随外激励幅值F变化而变化。随着外激励幅值F的增大，系统的分岔行为如下：周期运动→倍周期运动→混沌运动→倍周期运动→混沌运动。由表1可以看出，当控制参数ρ=0.4时，计算得到系统发生Smale马蹄变换意义下混沌的外激励幅值条件为F≥0.3914，通过将此时的系统分岔图与表1对照分析可知系统在F≥0.3914时进入混沌。

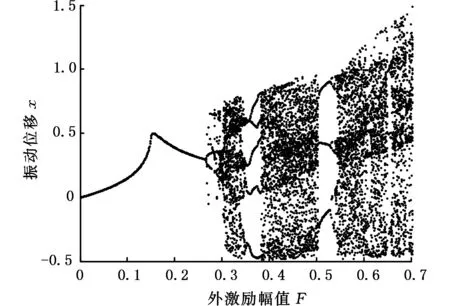
图5 ρ=0时的系统分岔图Fig.5 System bifurcation diagram when ρ=0

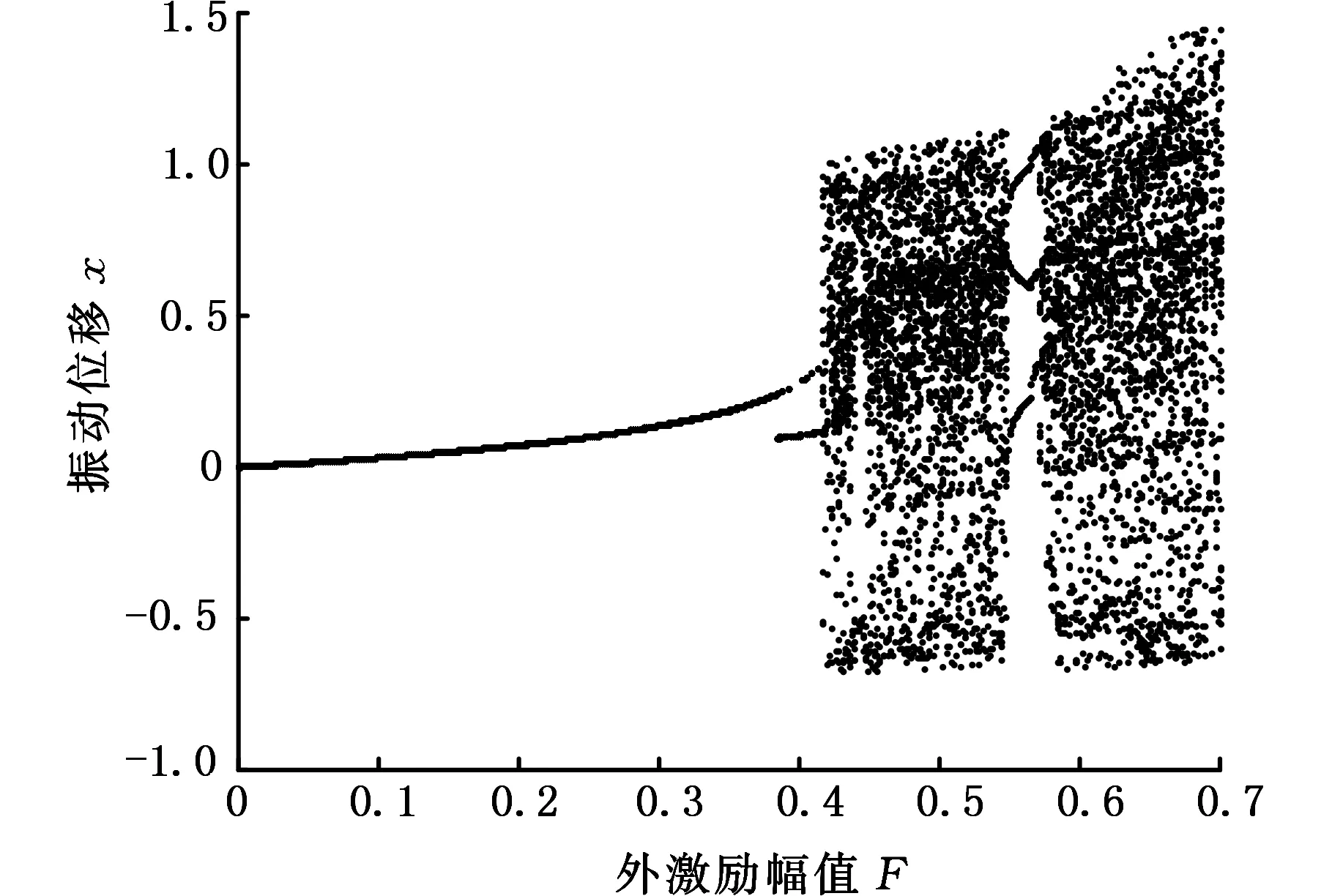
图6 ρ=0.4时的系统分岔图Fig.6 System bifurcation diagram when ρ=0.4

结合表1的计算结果和图4～图6所示的分岔图可知，随着线性控制参数ρ的增大，系统发生混沌的临界外激励幅值F增大。

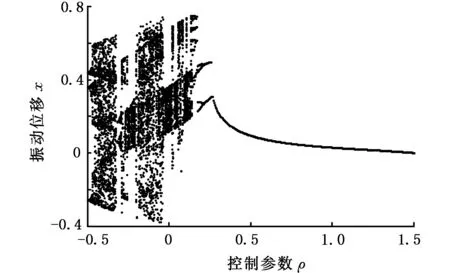
图7 ρ变化时的分岔特性Fig.7 Bifurcation characteristic when the ρ changes

5.2 控制分析

图7～图10为线性控制参数ρ不同时系统的分岔特性图。当F=0.3时，以线性控制参数ρ为分岔参数，通过系统的分岔图、相图和Poincare截面，分析系统随线性控制参数ρ变化的规律。

从图7可以看出，当线性控制参数ρ处于区间-0.5～1.5时，随着线性控制参数ρ的增大，系统的分岔行为由混沌运动逐渐转变为周期运动。在图8～图10中，当线性控制参数ρ=-0.2时，系统Poincare截面是一些有界的离散点集，表明系统是混沌运动。当线性控制参数ρ=0.22时，系统出现倍周期运动，而对应的Poincare截面为一个孤立的点。当线性控制参数ρ=0.4时，可看出系统相图为一封闭曲线，在Poincare截面上表现为一孤立的点，说明此时系统为周期运动。

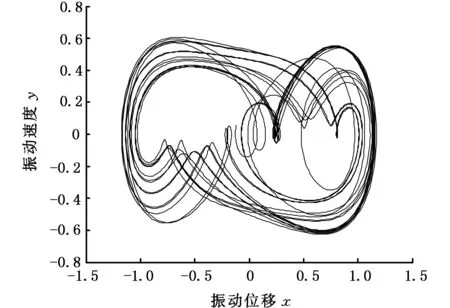
(a)相图

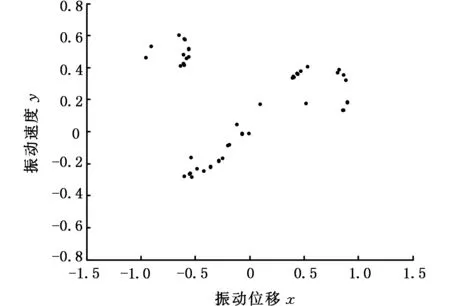
(b)Poincare截面图8 ρ=-0.2时系统的相图和Poincare截面Fig.8 Phase diagram and Poincare section of the system when ρ=-0.2

结合图7～图10的分岔图、相图和Poincare截面可以发现，适当地增大系统的线性控制参数ρ，可以提高系统的稳定性。

6 结论

(1)考虑液压缸的非线性刚度约束作用，建立了一种液压缸非线性刚度约束系统的动力学控制模型。

(a)相图

(b)Poincare截面图9 ρ=0.22时系统的相图和Poincare截面Fig.9 Phase diagram and Poincare section of the system when ρ=0.22

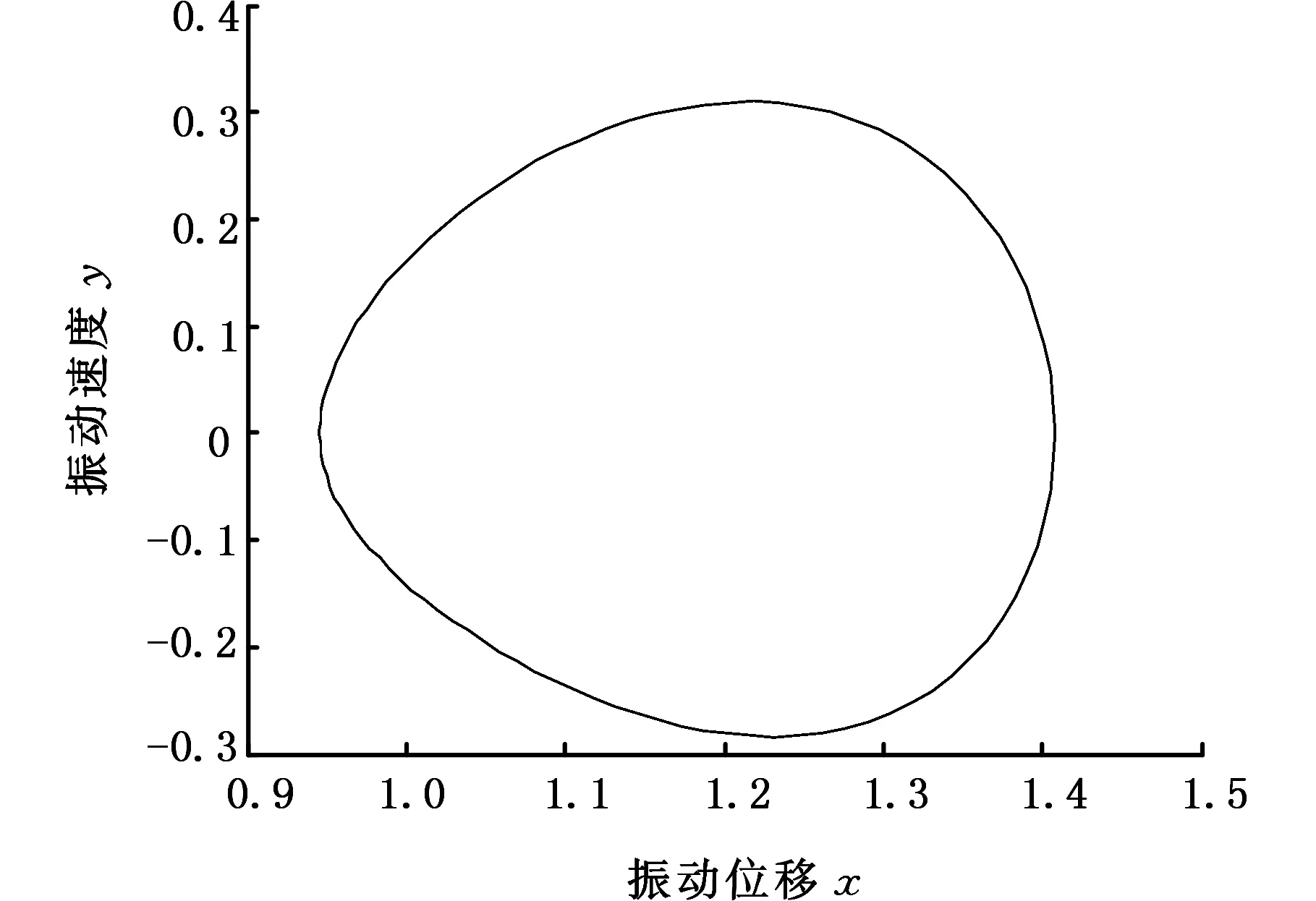
(a)相图

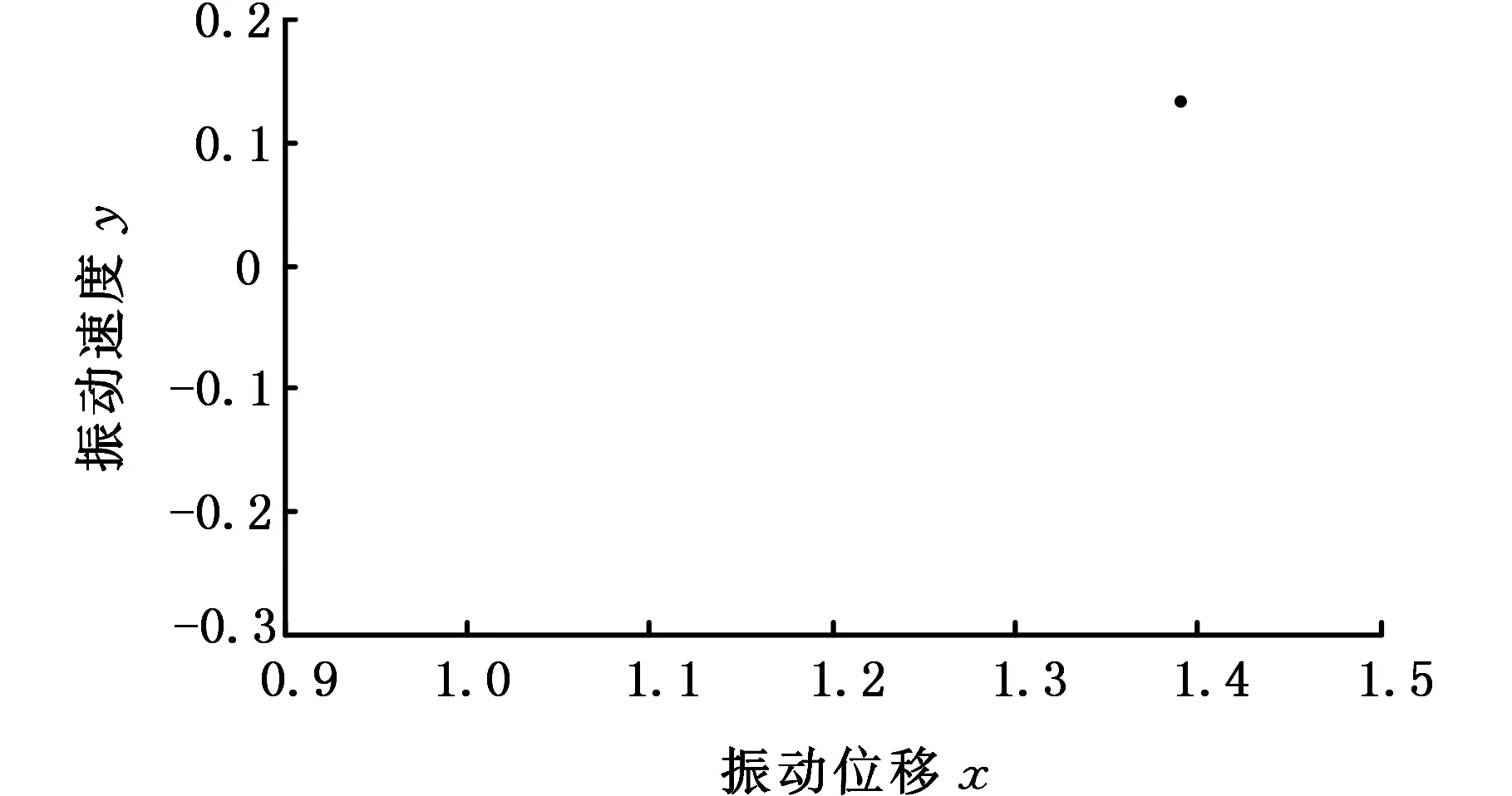
(b)Poincare截面图10 ρ=0.4时系统的相图和Poincare截面Fig.10 Phase diagram and Poincare section of the system when ρ=0.4

(2)在此动力学控制模型的基础上，建立了系统的量纲一动力学平衡方程，通过系统Melnkikov函数得到了系统发生Smale马蹄变换意义下混沌的临界条件。仿真分析了不同线性控制参数ρ对系统发生Smale马蹄变换意义下混沌临界条件的影响。

(3)分析了线性控制参数ρ变化下系统的分岔特性，得到了在一定范围内，随着线性控制参数ρ的增大，系统逐渐由混沌运动转变为稳定的周期运动。研究结果为这一类液压缸非线性约束系统的动力学控制提供了理论参考。

[1]BIYanhong,LUORuiying,LIJinsong,etal.TheEffectsoftheHydraulicOilonMechanicalandTribologicalPropertiesofC/CComposites[J].MaterialsScienceandEngineering, 2008, 483/484: 274-276.

[2] 朱勇，姜万录，刘思远，等. 非线性液压弹簧力对电液伺服系统非线性动力学行为影响的研究[J]. 中国机械工程, 2015, 26(8): 1085-1091.ZHUYong,JIANGWanlu,LIUSiyuan,etal.ResearchonInfluenceofNonlinearHydraulicSpringForceonNonlinearDynamicBehaviorsofElectro-hydraulicServoSystem[J].ChinaMechanicalEngineering, 2015, 26(8): 1085-1091.

[3]SEOJ,VENUGOPALR,KENNéJP.FeedbackLinearizationBasedControlofaRotationalHydraulicDrive[J].ControlEngineeringPractice, 2007, 15(12): 1495-1507.

[4] 傅晓云，黎飞，李宝仁. 某水下航行器舵机液压伺服系统建模仿真[J]. 机床与液压, 2010, 38(13): 151-153.FUXiaoyun,LIFei,LIBaoren.MathematicalModelingandSimulationofaUVHydraulicSteeringGearServoSystem[J].MachineTool&Hydraulics, 2010,38(13): 151-153.

[5]HAYASHIS.NonlinearPhenomenainHydraulicSystems[C]//ProceedingsoftheFifthInternationalConferenceonFluidPowerTransmissionandControl.Sendai, 2001: 28-32.

[6]MISRAA,BEHDINANK,CLEGHORNWL.Self-excitedVibrationofaControlValveduetoFluid-structureInteraction[J].JournalofFluidsandStructures, 2002, 16(5): 649-665.

[7]LICSKOG.NonlinearAnalysisofaSingleStagePressureReliefValve[J].InternationalJournalofAppliedMathematics, 2009, 39(4): 4-12.

[8] 王林鸿，吴波，杜润生，等. 液压缸运动的非线性动态特征[J]. 机械工程学报, 2007, 43(12): 12-19. WANG Linhong, WU Bo, DU Runsheng, et al. Nonlinear Dynamic Characteristics of Moving Hydraulic Cylinder[J]. Chinese Journal of Mechanical Engineering，2007，43(12)：12-19.

[9] 王林鸿，杜润生，吴波，等. 数控工作台的非线性动态特性[J]. 中国机械工程, 2006, 34(9): 118-122. WANG Linhong, DU Runsheng, WU Bo, et al. Nonlinear Dynamic Characteristics of NC Table[J].China Mechanical Engineering, 2009, 20(13): 1513-1519.

[10] 高普云. 非线性动力学-分叉、混沌与孤立子[M]. 北京：国防科学技术大学出版社, 2005:74-77. GAO Puyun. Nonlinear Dynamics-bifurcation, Chaos and Soliton[M]. Beijing: National University of DefenceTechnology Press, 2005:74-77.

[11] 刘彬, 赵红旭, 侯东晓. 一类含三势阱Mathieu-Duffing振子的相对转动系统的分岔和混沌[J]. 物理学报, 2014, 63(17): 180-188. LIU Bin, ZHAO Hongxu, HOU Dongxiao. Bifurcation and Chaos of Some Relative Rotation System with Triple-well Mathieu-duffing Oscillator[J]. Acta Physica Sinica, 2014, 63(17): 180-188.

[12] Vassilios M, Antonopoulos R C, Drossos L. Chaos in a Near-integrable Hamiltonian Lattice[J]. International Journal of Bifurcation and Chaos, 2002, 12(8): 1743-1754.

(编辑 王艳丽)

Chaotic Prediction and Control of Hydraulic Cylinder Nonlinear Stiffness Constraint System

LIU Bin1LI Peng1LIU Fei2LIU Haoran2JIANG Jiahao1

1.School of Electrical Engineering, Yanshan University, Qinhuangdao, Hebei, 066004 2.School of Information Science and Engineering, Yanshan University, Qinhuangdao, Hebei,066004

For the chaos of nonlinear stiffness constraint system of a hydraulic cylinder, a kind of dynamic control model of hydraulic cylinder nonlinear stiffness constraint system was established. The critical conditions of chaos in nonlinear stiffness constraint system of the hydraulic cylinder in the sense of Smale’s horseshoe transformation were obtained by Melnikov method. Through simulation analyses, it is found that when the linear control parameters are changed, the critical conditions for the occurrence of chaos in the system will also change. At the same time, the stability of the system may be improved when the linear control parameters are increased.

hydraulic cylinder; constraint system; Melnikov method; chaos; control

2016-04-19

河北省自然科学基金资助项目(E2015203349)

TH113；O322

10.3969/j.issn.1004-132X.2017.05.009

刘 彬，男，1953年生。燕山大学电气工程学院教授、博士研究生导师。主要研究方向为轧机振动及测量技术。发表论文50余篇。E-mail：liubin@ysu.edu.cn。李 鹏，男，1990年生。燕山大学电气工程学院硕士研究生。刘 飞，男，1986年生。燕山大学信息科学与工程学院博士研究生。刘浩然，男，1980年生。燕山大学信息科学与工程学院副教授。姜甲浩，男，1991年生。燕山大学电气工程学院硕士研究生。