钳夹车双层并联过约束机构力学解算与均载性分析

赵延治 焦雷浩 王向南 任玉波 魏鸿亮 于跃斌

1.燕山大学河北省并联机器人与机电系统重点实验室，秦皇岛,0660042.先进锻压成形技术与科学教育部重点实验室(燕山大学)，秦皇岛,0660043.中车齐齐哈尔车辆有限公司，齐齐哈尔，161002

钳夹车双层并联过约束机构力学解算与均载性分析

赵延治1,2,3焦雷浩1,2王向南1,2任玉波1,2魏鸿亮3于跃斌3

1.燕山大学河北省并联机器人与机电系统重点实验室，秦皇岛,0660042.先进锻压成形技术与科学教育部重点实验室(燕山大学)，秦皇岛,0660043.中车齐齐哈尔车辆有限公司，齐齐哈尔，161002

为研究钳夹车双层并联过约束起升机构力传递与均载特性，基于Timoshenko梁理论建立了起升机构钳形梁刚度模型，通过联立该双层并联过约束机构弹性变形协调方程与静力平衡方程，对起升机构进行了力学解算，得到了机构分支承载力与机构刚度的映射关系。在此基础上，定义了不均衡载荷系数，分析得到了机构刚度变化及其载运偏载量对起升机构均载性能的影响规律。基于动力学仿真软件RecurDyn建立了双层并联过约束起升机构的刚柔耦合仿真模型，仿真分析结果验证了理论建模分析的正确性。

钳夹车；双层并联机构；过约束；均载

0 引言

铁路特种货物运输钳夹车承担着特高压输电、油气管线和航母制造等关乎国计民生的重特大工程中超重超限大型关键设备的运输[1]。经过多年的发展，我国已经从钳夹车的仿制阶段迈入到了自主研制生产阶段[2]，如中国中车齐齐哈尔交通装备有限公司研制的DQ45型钳夹车。钳夹车自重和负载超大，运输的安全性须严格保证，特别是其用于起升和夹持货物的起升机构的稳定性与安全性至关重要。起升机构实质为双层并联过约束机构，其力学解算较为复杂。

在有关钳夹车载荷解算和过约束机构受力分析方面，许多学者展开了相关研究,如万朝燕等[3]对钳夹车压柱油缸的稳定性进行了研究；范国海等[4]对钳夹车的受力稳定性进行了分析；聂春戈等[5]基于能量法对压柱油缸的受力进行了解算；朴明伟等[6]采用刚柔耦合仿真方法对钳夹车进行了分析，得到了其受力与变形情况；赵永生等[7]提出了一种对并联过约束机构受力的数值仿真分析方法。

本文基于Timoshenko梁理论对钳形梁模型进行刚度建模，并对钳夹车双层并联过约束机构进行力学解算，定义了不均衡载荷系数，分别基于刚度和偏载分析了该双层并联过约束机构的均载特性。

1 起升机构钳形梁刚度建模

钳夹车起升机构实质上为一双层并联过约束机构，其机构简图见图1。货物位于钳夹车起升机构中部，四条钳形梁分别位于起升机构两侧并与货物相连，是提升机构的主体结构，因此，钳形梁的刚度直接影响整体提升机构的力学解算。

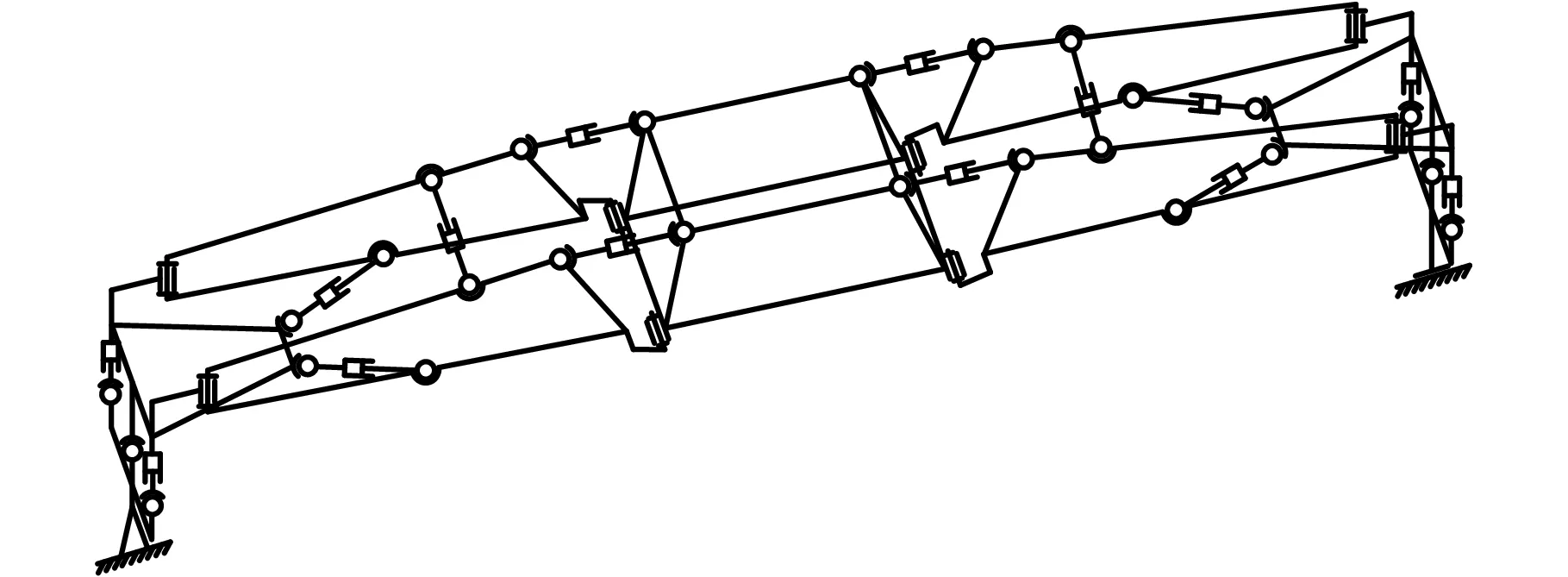
图1 钳夹车起升机构简图Fig.1 The diagram of lifting mechanism

1.1 Timoshenko梁单元刚度矩阵

基于Timoshenko梁理论，分别对单元节点的轴向位移、挠度和截面转角进行独立插值，构造Timoshenko梁单元对钳形梁进行刚度建模与计算。钳形梁离散结果如图2所示。

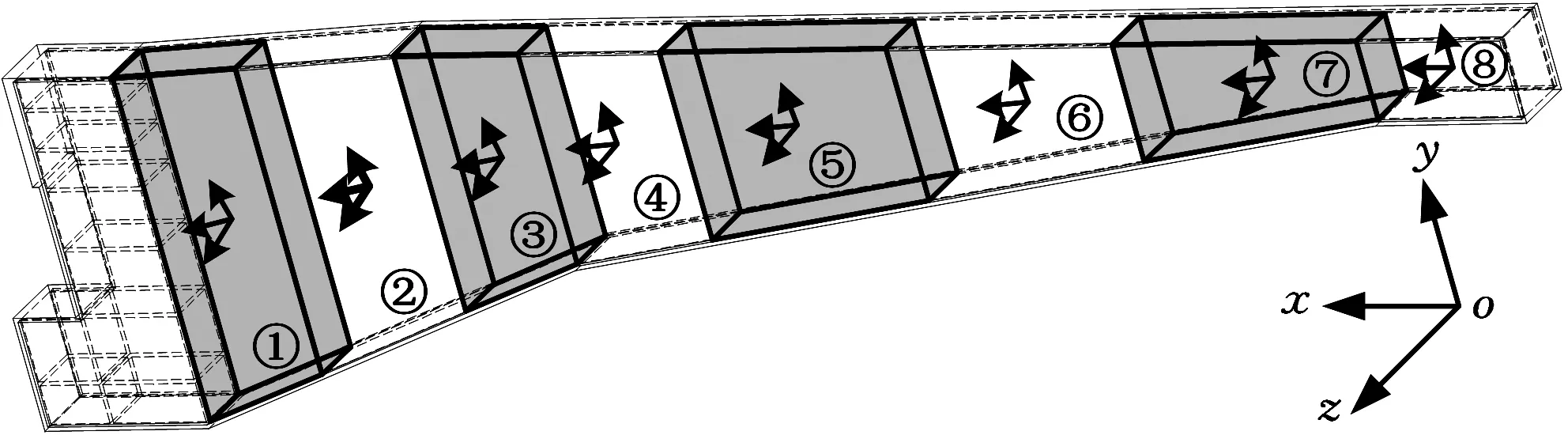
图2 钳形梁离散图Fig.2 The discrete graph of schnabel

设单元总长为l，节点轴向位移为u，单元总挠度为v，截面转角为θ，根据Timoshenko梁理论定义其插值模式为

(1)

式中,ur为单元r(r=1,2)的轴向位移；vr为单元r的总挠度；θr为单元r的截面转角；x为单元r的x轴位移自变量。

其中形状函数：

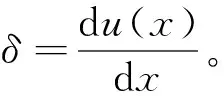
结合单元插值模式(式(1))可得

(2)

单元的势能泛函数为

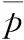
将式(2)代入式(1)，并令式(1)取驻值，整理可得单元刚度方程：

Keδe=fe+pe

则单元刚度矩阵为

Ke=Ka+Ks+Kc

式中，Ka、Ks、Kc分别为单元的拉压、剪切、弯曲刚度矩阵。

1.2 钳形梁的刚度矩阵

整体刚度矩阵的计算须将定义在各单元局部坐标系下的力与位移转换到钳形梁的整体坐标系下[9]，整体坐标系与局部坐标系位置如图2所示，设其转换矩阵为

式中，l、m、n分别为节点局部坐标x、y、z轴相对于整体坐标的矩阵转换列矢量。

设局部坐标系中梁单元的节点位移列阵为

q1=[u10v10θ10u20v20θ20]T

整体坐标系中梁单元的节点位移列阵为

对于节点1，具体转换关系如下：

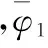
同理，对于节点2，将具体转换关系合并得坐标变换矩阵为

采用叠加法将其组装成整体刚度矩阵，将单元刚度矩阵按照节点写成分块模式，以第一个离散单元为例：

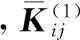
再将分块矩阵按照下述形式叠加，可得钳形梁的整体刚度矩阵：

K=

2 双层过约束起升机构力学解算

2.1 双层并联过约束起升机构

钳夹车起升机构为中心对称结构，保留货物及钳形梁部分，简化后的起升机构如图3所示。

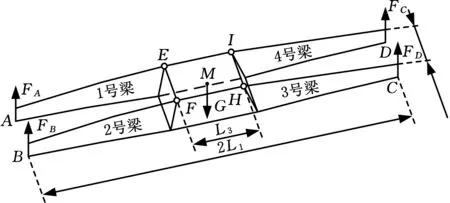
图3 简化后的起升机构Fig.3 The simplified diagram of lifting mechanism

钳形梁与货物的连接点分别为E、F、H、I，钳形梁与底架连接点分别为A、B、C、D，M为起升机构的重心。其中AE段为1号梁，BF段为2号梁，CH段为3号梁，DI段为4号梁，与钳形梁相连的油缸取相同的编号。机构总长为2L1，钳形梁末端宽度为2L2，货物的长度为L3。机构整体所受外力包括机构的重力G和4个钳形梁末端的支反力分别为FA、FB、FC、FD。

2.2 起升机构静力解算

图3所示起升机构的静力平衡方程如下：

(3)

设钳形梁为柔性体，根据钳形梁的变形情况增加变形协调方程[10]。由于货物为刚性体，当起升机构受力变形后，点E、F、H、I构成平面仍为平面，设其与平面P重合，如图4所示。

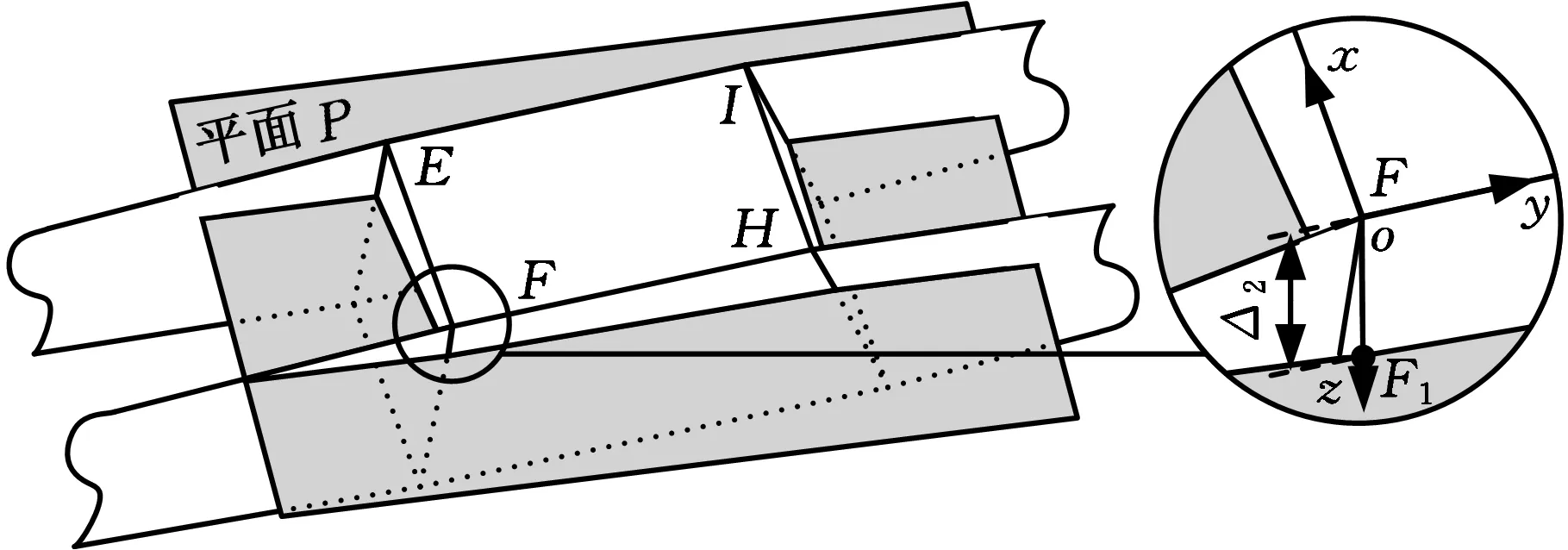
图4 起升机构变形示意图Fig.4 The deformation diagram of lifting mechanism

设4个钳形梁的变形量分别为Δ1、Δ2、Δ3、Δ4，以点F为例，根据小变形原理设机构变形后点F1位于点F的正下方，位置如图4所示。在F点处建立笛卡儿坐标系oxyz，则平面P的方程为

(4)

I1点表示钳形梁变形后，I点正下方对应点，其坐标为(L2，L3，Δ4)，将其代入式(4)，可以得到关于Δ1、Δ2、Δ3、Δ4的变形协调方程：

(5)

钳形梁的变形量可以根据刚度方程来求解，简写为

式中,Ki(i=1,2,3,4)为各钳形梁的刚度。

将其代入变形协调方程(式(5))可得附加力平衡方程：

(6)

联立4个平衡方程(式(3)和式(6))，即可解得基于刚度的各钳形梁支反力。

2.3 机构输入输出力映射

由静力解算结果可知，压柱油缸力与各钳形梁的刚度相关。为全面系统地研究刚度对机构力映射的影响，采用空间性能图谱理论，对钳形梁的刚度进行量纲一处理[11]，令

(7)

其中，ki为钳形梁i相对刚度，为量纲一参数，由式(7)得

k1+k2+k3+k4=1

令k4=0.25，分析其他钳形梁刚度变化对油缸力的影响。首先分析货物不存在偏心的情况，取货物质量为300 t时，1号和2号钳形梁上的压柱油缸受力与钳形梁相对刚度之间的关系，如图5所示。

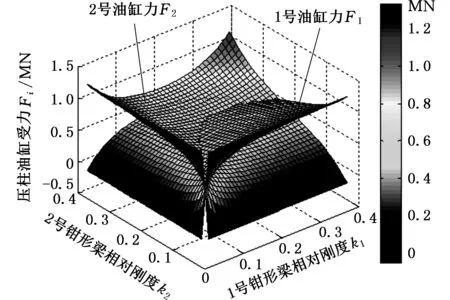
图5 1、2号油缸受力与刚度变化关系Fig.5 The relationship between the force and the stiffness of the cylinder with number one and two

图5中绘制出的两个曲面，分别表示1(3)号油缸和2(4)号油缸的输入力，两曲面间的交线代表4个油缸的输入力大小相等，此时起升机构处于完全均载状态。两曲面的差值表示油缸输入力的差值，绘制出的等高线图如图6所示,图中数值单位为N。

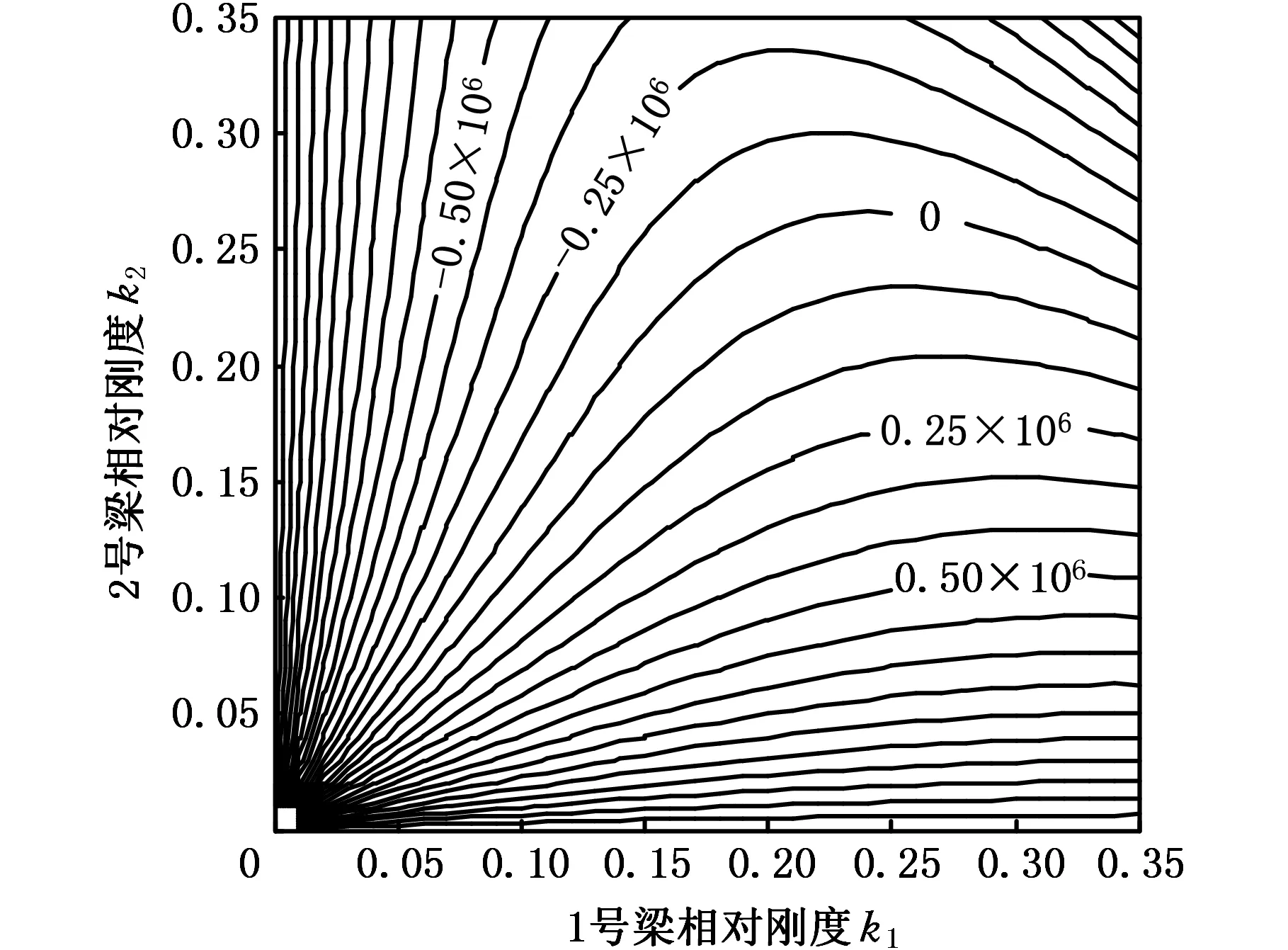
图6 均载情况下1、2号油缸的输入力差值Fig.6 The input force difference of the number one and two cylinder when loaded with balanced force

图6中，随着分支刚度的不同，起升机构的油缸输入力差值相应变化，图中的“0”线，表示机构处于完全均载情况下。

3 起升机构均载性分析

为了有效衡量起升机构的均载特性，定义不均衡载荷系数[12]：以4个油缸输入力最大值与最小值的比值k作为机构的不均衡载荷系数，用以衡量机构的均载特性，如下式所示：

(8)

式中，Fmax为各压柱油缸输入力最大值；Fmin为各压柱油缸输入力最小值。

图7所示为在货物存在偏心距的情况下分支刚度与4个压柱油缸输入力的关系，图中4个曲面无公共点，即各油缸输入力的无法完全相等，机构无法实现完全均载。

图7 某偏心距下各油缸输入力变化Fig.7 The input force variation of each cylinder under eccentric distance

3.1 货物偏心对机构均载性的影响

由静力平衡方程(式(3))可得

(9)

式(9)表明当货物的偏心距确定时，压柱油缸1与3的输入力差值恒定，压柱油缸2与4的输入力差值也恒定。当货物存在某偏心距时，油缸1和2输入力与钳形梁相对刚度的关系分别如图8、图9所示。

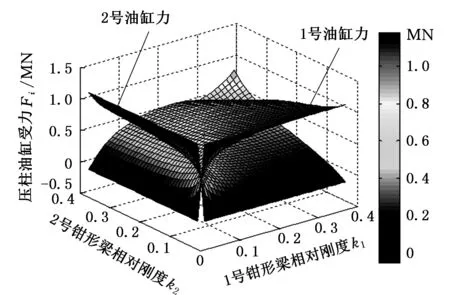
图8 1、2号油缸梁输入力变化曲面Fig.8 The input force change surface of the cylinder with number one and two

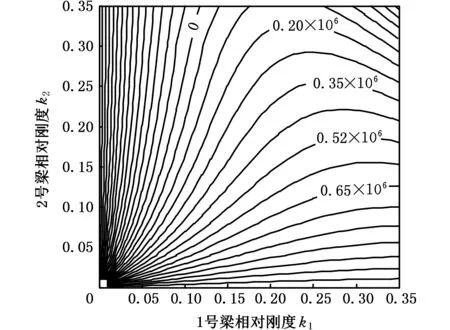
图9 不均载情况下1、2号油缸输入力差值Fig.9 The input force difference of the number one and two when loaded with unbalanced force

图9绘制的等高线代表1、2号压柱油缸输入力的差值，图中存在“0”线，即1号油缸与2号油缸的输入力相等，然而这并非机构均载的最优情况，因为此时3号油缸与4号油缸的输入力差值较大，这是由于各分支刚度差异导致的。

起升机构货物只存在偏心的情况下偏心距与不均衡载荷系数k的关系如图10和图11所示。

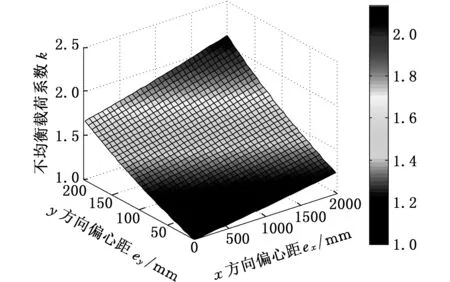
图10 偏心距与不均衡载荷系数的变化关系Fig.10 The relationship between eccentricity and unbalanced load coefficient

图11 不均衡载荷系数随偏心距变化的等高线图Fig.11 The contour map of the variation of unbalanced load coefficient with eccentricity

图10表示偏心距与不均衡载荷系数的关系，其等高线图见图11。可见，不均衡载荷系数变化较为均匀，机构y轴方向上的偏心对起升机构均载性的影响大于x轴方向偏心对起升机构均载性的影响。

3.2 分支刚度对机构均载性的影响

当起升机构的货物无偏心，各分支刚度不同时，在某刚度变化范围内刚度与不均衡载荷系数k的关系如图12所示。取图12中曲面的中间部分绘制的刚度与不均衡载荷系数k关系的等高线图见图13。

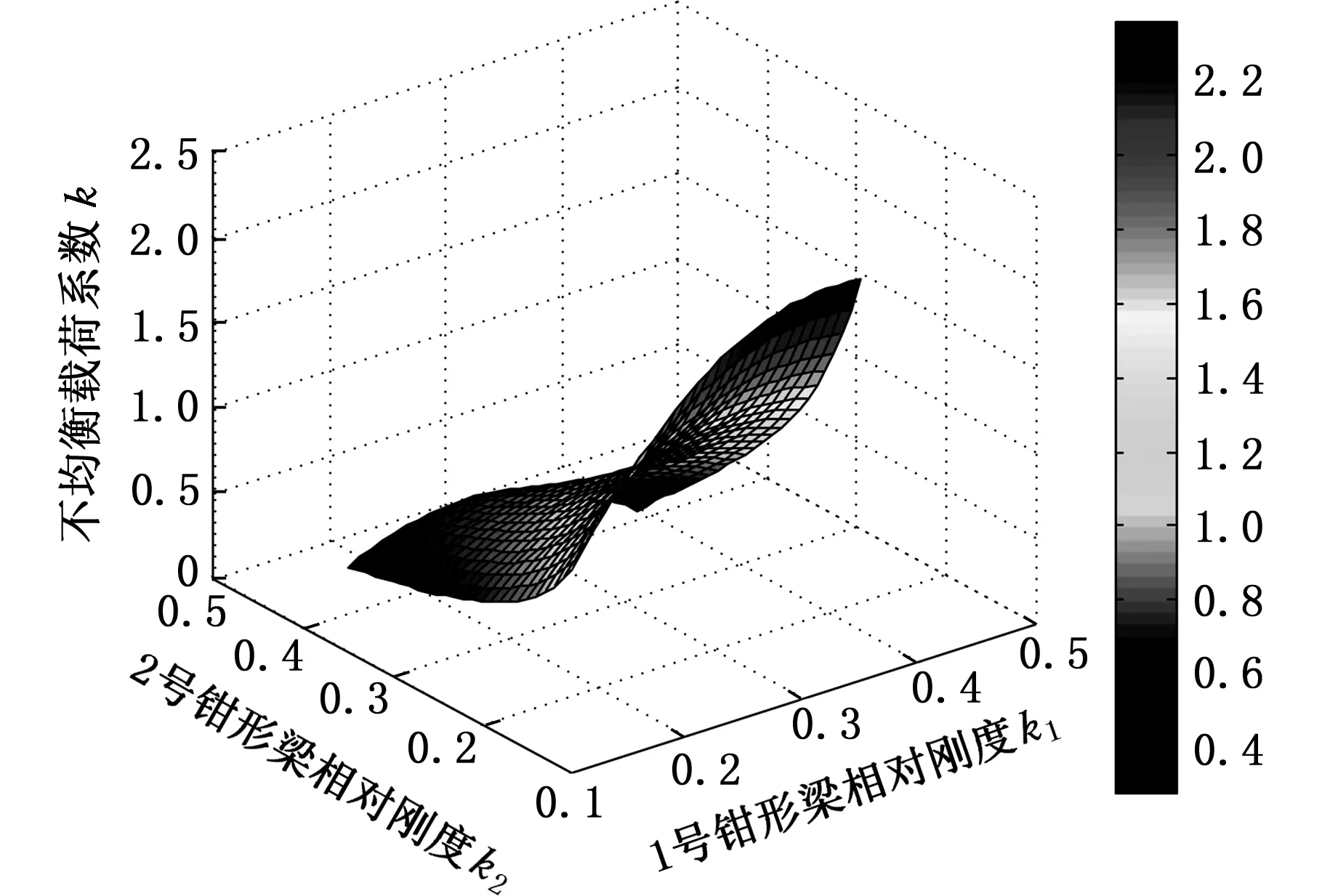
图12 不均衡载荷系数与刚度的变化关系Fig.12 The relationship between the unbalance load coefficient and the stiffness

图13 不均衡载荷系数随刚度变化的等高线图Fig.13 The contour map with the variation of the load coefficient with the variation of the stiffness

从图13中等高线分布可以看出，y轴所对应的分支刚度对不均衡载荷系数的影响大。从机构的结构角度来说，对角分支(“1、3分支”或“2、4分支”)刚度相近，更有利于提高机构的均载性能。

4 起升机构刚柔耦合仿真

采用多体动力学仿真软件RecurDyn[13]对钳夹车起升机构进行刚柔耦合仿真分析，得到的起升机构刚柔耦合仿真模型如图14所示。

图14 起升机构刚柔耦合仿真模型Fig.14 The rigid flexible coupling simulation model of the lifting mechanism

取每次仿真中点(80 s)的数据与计算结果进行对比。当货物存在偏心，各分支刚度相同时，理论计算结果与仿真结果对比如图15所示。

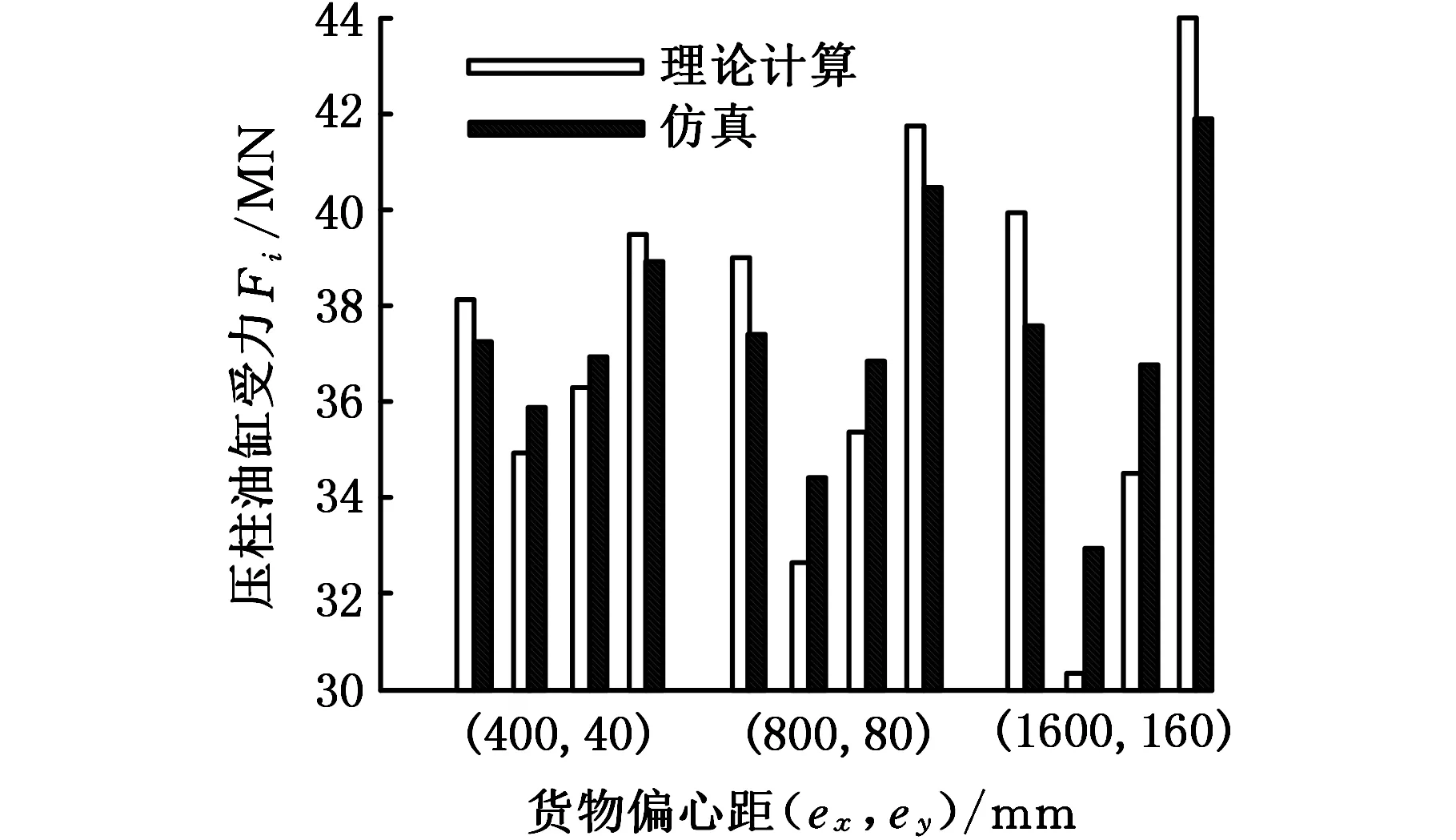
图15 理论计算与仿真计算结果对比Fig.15 The comparison of theoretical calculation and simulation results

图15中，每个偏心距对应一组数据，每组数据依次为4个油缸输入力的理论计算结果与仿真计算结果。当货物无偏心时，理论计算结果与仿真计算结果吻合，当货物存在偏心时，理论计算结果与仿真结果存在偏差，平均偏差为5.1%。相对于理论计算结果，仿真计算结果较为收敛，这是由于仿真计算考虑了机构的变形和货物的转动，使得各油缸输入力更趋向于平均。

当货物各分支的刚度不一致时，理论计算结果与仿真计算结果对比如图16所示。图中横坐标三组数据分别为1/2/3/4号钳夹梁相对刚度。

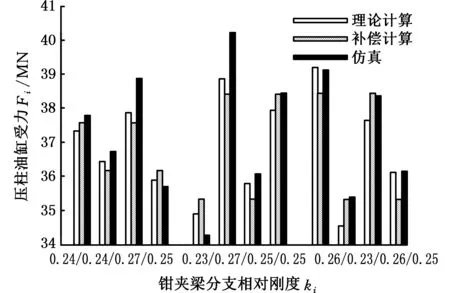
图16 计算与仿真结果对比Fig.16 The comparison of calculation and simulation results

图16中每组钳形梁相对刚度匹配对应一组数据，每组数据依次为4个油缸输入力的理论计算结果、补偿计算结果和仿真结果。图中理论计算与仿真的平均偏差为1.76%，补偿计算与仿真的平均偏差为1.42%。

5 结语

本文提供了一种钳形梁刚度建模的简便方法，基于刚度模型对双层并联过约束起升机构进行了静力解算，得到了起升机构静力解析解。通过定义钳夹车起升机构不均衡载荷系数，分析得到分支刚度和载运偏载对机构受力和均载性的影响规律，通过刚柔耦合仿真计算分析对理论建模与计算结果进行了验证。

[1] 田葆栓. 铁路长大货物运输对国家重点建设的贡献[J]. 中国铁路, 2010(3):14-16. TIAN Baoshuan. The Contribution to National Key Construction of Long-freight Railway Rransportation [J]. China Railway, 2010(3):14-16.

[2] 田葆栓. 我国长大货物车的最新进展与关键技术问题[J]. 铁道车辆, 2005(1):15-18. TIAN Baoshuan. The Recent Advances and Key Technology Problem of Long-freight Cars in China [J]. Railway Vehicles, 2005(1):15-18.

[3] 万朝燕, 朴明伟, 兆文忠, 等. 350吨钳夹车压柱油缸稳定性分析[J]. 大连交通大学学报, 2008, 29(5): 27-33. WAN Zhaoyan, PU Mingwei, ZHAO Wenzhong. Stability Analysis of Press Cylinder of 350 Tons Schnable Car [J]. Journal of Dalian Jiaotong University, 2008, 29(5): 27-33.

[4] 范国海, 关晓丽, 王文, 等. DQ35型钳夹车车体性能仿真及验证[J]. 铁道车辆, 2008, 46(3): 1-6. FAN Guohai, GUAN Xiaoli, WANG Wen. Vehicle Performance Simulation and Validation of DQ35 Schnabel Car [J]. Railway Vehicles, 2008, 46(3): 1-6.

[5] 聂春戈, 魏鸿亮, 兆文忠. 钳夹车液压举升系统的简化分析[J]. 铁道车辆, 2014(9):11-13. NIE Chunge, WEI Hongliang, ZHAO Wenzhong. Simplified Analysis of Hydraulic Lifting System of Schnabel Car [J]. Railway Vehicles,2014(9):11-13.

[6] 朴明伟, 郭强, 兆文忠. 450t钳夹车研制及刚柔耦合动态仿真技术支持[J]. 大连交通大学学报, 2015, 36(3):9-13. PU Mingwei, GUO Qiang, ZHAO Wenzhong. Development and Rigid Flexible Coupling Dynamic Simulation Technology Support of 450t Schnabel Car [J]. Journal of Dalian Jiaotong University, 2015, 36(3):9-13.

[7] 赵永生, 刘文兰, 许允斗, 等. 一种过约束并联机构受力的数值仿真分析方法[J]. 中国机械工程, 2015，26(12): 1576-1583. ZHAO Yongsheng, LIU Wenlan, XU Yundou, et al. A Numerical Simulation Method for Force Analysis of an Overconstrained PM [J]. China Mechanical Engineering, 2015,26(12): 1576-1583.

[8] 传光红, 陈以一, 童根树. 变截面Timoshenko梁的单元刚度矩阵[J]. 计算力学学报, 2014(2):265-272. CHUAN Guanghong, CHEN Yiyi, TONG Genshu. Stiffness Matrix of Timoshenko Beam with Variable Cross-section [J]. Journal of Computational Mechanics, 2014(2):265-272.

[9] 徐荣桥.结构分析的有限元法与MATLAB程序设计[M].北京:人民交通出版社, 1996:44-68. XU Rongqiao. The Finite Element Method of Structural Analysis and the Design of MATLAB Program [M]. Beijing: the People's Communication Publishing Company， 1996:44-68.

[10] 韩玮, 刘志军. 基于平面法求解刚性支承平面多点支承的反力[J]. 建筑机械, 2013(4):100-101. HAN Wei, LIU Zhijun. The Solution of Point-supported Reaction in Rigid Plane Based on Planar Method [J]. Construction Machinery, 2013(4):100-101.

[11] 刘辛军. 并联机器人机构尺寸与性能关系分析及其设计理论研究[D]. 秦皇岛：燕山大学, 1999. LIU Xinjun. Research on Relationship between Size and Performance of Parallel Robot Mechanism and Design Theory [D]. Qinhuangdao: Yanshan University, 1999.

[12] 戴杰. 吊车吊装附加载荷及载荷系数[J]. 石油工程建设, 1996(3):44-48. DAI Jie. Additional Load and Load Factors of Lifting Crane [J]. Petroleum Engineering Construction, 1996(3):44-48.

[13] 刘义. RecurDyn多体动力学仿真基础应用与仿真[M]. 北京:电子工业出版社, 2013:452-488. LIU Yi. Application and Simulation of RecurDyn Multi-body Dynamics Simulation [M]. Beijing: Electronic Industry Publishing Company, 2013:452-488.

(编辑 王艳丽)

Static Calculation and Load Sharing Characteristics Analysis of Double Parallel over Constrained Lifting Mechanisms of Schnabel Car

ZHAO Yanzhi1,2,3JIAO Leihao1,2WANG Xiangnan1,2REN Yubo1,2WEI Hongliang3YU Yuebin3

1.Hebei Provincial Key Laboratory of Parallel Robot and Mechatronic System,Yanshan University,Qinhuangdao,Hebei,066004 2.Key Laboratory of Advanced Forging & Stamping Technology and Science(Yanshan University) Ministry of Education of China,Qinhuangdao,Hebei,066004 3.CRRC Qiqihaer Vehicle Limited Corporation,Qiqihaer,Heilongjiang,161002

To research the constraint forces and load sharing characteristics of double parallel over constrained lifting mechanisms of schnabel car, a stiffness model of schnabel beam was established based on Timoshenko beam theory. The static calculation was done by simultaneous equations solution of elastic deformation coordination equations and static force balance equations, and the mapping relationships among the bearing capacities and stiffnesses of the mechanisms were obtained. Then, the unbalanced load coefficients of the lifting mechanisms were defined, and the influence rule of load sharing characteristics produced by structure stiffness changes and partial loads were analysed and obtained. The rigid-flexible coupled simulation model of double parallel over constrained lifting mechanisms was built in RecurDyn and the simulation results verified the correctness of theoretical analyses.

schnabel car; parallel lifting mechanism; over constrained; load sharing

2016-02-17

国家自然科学基金资助项目(51105322);河北省自然科学基金资助项目(E2014203176);河北省高等学校自然科学研究青年基金资助项目(QN2015040);中国博士后科学基金资助项目(2016M590212)

TH112

10.3969/j.issn.1004-132X.2017.05.012

赵延治，男，1981年生。燕山大学机械工程学院副教授。主要研究方向为并联机器人机构学理论与应用。发表论文30余篇。焦雷浩，男，1990年生。燕山大学机械工程学院硕士研究生。王向南，男，1989年生。燕山大学机械工程学院硕士研究生。任玉波，女，1963年生。燕山大学机械工程学院副教授。魏鸿亮，男，1969年生。中车齐齐哈尔车辆有限公司研究员级高级工程师。于跃斌，男，1970年生。中车齐齐哈尔车辆有限公司研究员级高级工程师。