一个基本模型背后的“深思”*

☉江苏南师大附中新城初中 何君青☉江苏南师大附中新城初中 陈敏婕

一个基本模型背后的“深思”*

☉江苏南师大附中新城初中 何君青☉江苏南师大附中新城初中 陈敏婕

数学教学过程中最重要的环节就是以数学知识、技能为载体，渗透数学思想方法，从而让学生体会一类数学问题的本质，这样才能提高学生的数学能力.笔者在长期的教学过程中，发现有些类型的题目无论对作为新知识学习的学生还是经过系统复习后面临中考的学生来说都有一定困难，这类题特别值得关注.本文就以最短路径问题与读者交流，共同探讨教学过程中的一些收获.

一、基本模型

顾名思义，最短路径问题其中有一类就是寻找两条线段或多条线段的最小值问题.这类问题贯穿整个初中三年，从初一到初三都是常考问题，在中考模拟题或中考题中也时常出现，此类题也是学生常错的问题.

这类问题的题源还要从一个课本练习题说起：

如图1，A、B两点在直线l的同侧，在l上找一点P，使PA+PB最小.

图1

图2

分析：先作点B关于直线l的对称点B′（如图2），则PB=PB′.所以，求PA+PB的最小值相当于求PA+PB′的最小值，故当A、P、B′共线时AP+PB′的值最小.因此连接AB′，AB′与直线l的交点，就是点P.事实上，很多看似困难的最短路径问题，都可以转换成这个基本模型，利用上述方法使问题迎刃而解.

二、两条线段的最短路径问题

探究1：三角形中的最短路径.

如图3，在等边△ABC中，AB=2，点E是AB的中点，AD是△ABC的高，在AD上找一点P，使BP+PE的值最小，并求出最小值.

图3

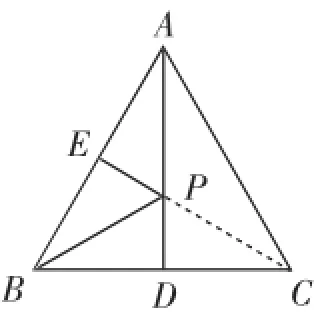
图4

分析：上述问题可以转换成模型：E、B在线段AD的同一侧，在AD上求作一点，使得PE+PB最小.如图4，作点B关于AD的对称点，恰好与点C重合，则BP=CP，若使BP+ PE的值最小，即使CP+PE的值最小，当C、P、E三点在同一条直线上时，满足CP+PE的值最小，故连接CE交AD于一点，则这点就是点P，由此可得BP+PE的最小值为

探究2：正方形中的最短路径.

如图5，正方形ABCD中，AB=2，E为BC的中点，在对角线BD上找一点P，使CP+PE的值最小，并求出最小值.

图5

图6

分析：上述问题仍然可以转换成模型：E、C在线段BD的同一侧，在BD上找一点P，使PE+PC最小.如图6，作点C关于BD的对称点，恰与点A重合，则AP=CP，若使EP+ CP的值最小，即使AP+PE的值最小，当A、P、E三点在同一直线上时，满足AP+PE的值最小，故连接AE交BD于一点，则这点就是点P，由此可得CP+PE的最小值为

探究3：菱形、矩形等图形中的最短路径.

如图7，菱形ABCD中，AC=8，BD=6，点M、N分别是AB、BC的中点，在对角线AC上找一点P，使MP+PN的值最小，并求出最小值.

图7

图8

分析：如图8，利用上述方法，可以很快求出PM+PN的最小值为5.

总结：通过探究1、探究2、探究3，我们可以发现在常见的轴对称图形中，解决最短路径的问题往往是通过转换成基础模型的方法，再利用共线点的最小值来求得答案.

探究4：平面直角坐标系中的最短路径.

如图9，在平面直角坐标系中，A（6，4）、B（4，6）、C（0，2），在x轴上找一点D，使四边形ABCD的周长最小，则点D的坐标是_____________.

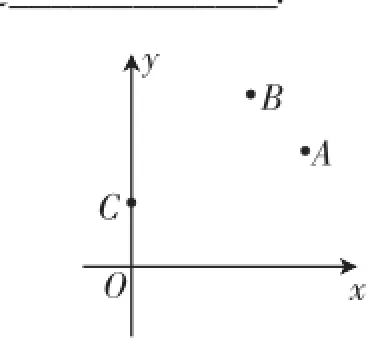
图9

分析：由于四边形ABCD中AB、BC的长度保持不变，所以求四边形ABCD周长的最小值就是求CD+AD的最小值，问题迅速转换成基本模型：A、C在x轴的同一侧，在x轴上求作一点，使DA+DC最小.故作点A关于x轴的对称点A′，则AD=A′D.若使CD+AD的值最小，即使得CD+ A′D的值最小，当C、D、A′三点共线时，CD+A′D的值最小，故连接A′C交x轴于一点，这点就是点D，通过此思路可得到点D的坐标.

探究5：圆中的最短路径.

图10

图11

分析：如图11，上述问题依然可以转换成模型：A、B在线段CD的同侧，在CD上找一点P，使BP+AP的值最小.故可以作点B关于线段CD的对称点E，根据圆的对称性，点E在圆上，则PB=PE，若使BP+AP的值最小，即使AP+ PE的值最小，当A、P、E三点共线时，满足AP+PE的值最小，故AE交CD于一点，这点便是点P.

三、三条线段的最短路径问题

两条线段的最短路径问题通过上述几个例子已经掌握了其中的方法，只要将问题转换成基本模型，便可以解决，如果换成三条线段的最短路径问题，又该如何解决呢？

探究1：三角形周长的最短路径.

如图12，∠MON是锐角，它的内部有一点A，在OM上作一点B，在ON上作一点C，使△ABC的周长最小.

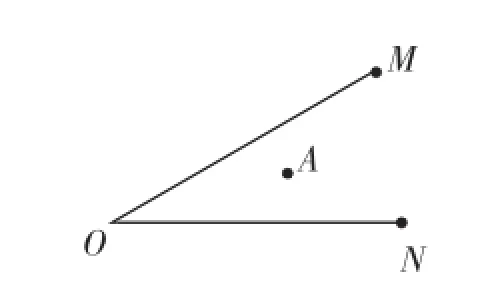
图12

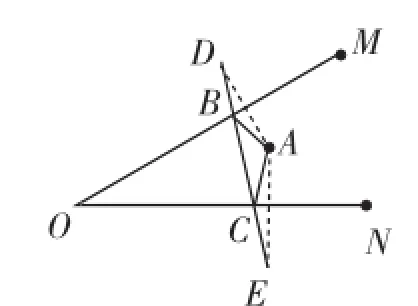
图13

分析：△ABC的周长由AB、BC、CA共同决定，先作出点A关于OM的对称点D，关于ON的对称点E（如图13），则BA=BD，CA=CE.从而求AB+BC+CA的最小值转换成求DB+BC+CE的最小值，显然当D、B、C、E四点共线时DB+ BC+CE的值最小.因此DE与OM、ON的交点，就分别是点B、点C.

此题还可以具体化：

变式：∠MON=30°，点A是∠MON内部任意一点，OA=8，在OM上作一点B，在ON上作一点C，使△ABC的周长最小，并求出最小值.

探究2：四边形周长的最短路径.

如图14，在平面直角坐标系中，有A（3，3）、B（1，5）、C（0，a）、D（b，0）四点，当四边形ABCD的周长最小时，求a、b的值.

图14

分析：由于四边形ABCD中A、B两点的位置已经确定，故AB的长度保持不变，所以想求四边形ABCD周长的最小值就是求BC+CD+DA的最小值，问题迅速转换成模型：A、B两点在∠yOx内部，在y轴、x轴上分别求作点C、D，使BC+CD+DA最小.

作点A关于x轴的对称点A1，根据对称性可知AD= A1D，作点B关于y轴的对称点B1，根据对称性可知BC= B1C.若使BC+CD+DA的值最小，即使得B1C+CD+DA1的值最小，当B1、C、D、A1四点在一条直线上时，满足B1C+CD+ DA1的值最小，故连接A1B1，与y轴、x轴有交点，就是所求的点C、点D，于是先算出直线A1B1的解析式，便可得到点C、点D的坐标，a、b的值也随之得到.

四、实践后的反思

1.关注数学问题的生长点.

很多教师经常会有这样的困惑：上课时已经提出了有价值的问题，很多学生却掌握不了，该如何教学？其实，我们常常发现一些刚讲过的问题学生很快就会忘掉，似乎在学生的记忆中从未留下“痕迹”，这主要是教学的过程中只关注了结果，并未关注过程所导致的.教学中，我们常告诉学生某个重要的结论，但却忽略了知识的形成和发展过程，如上面的例子，题源学生都见过，但如何灵活运用、怎么去运用，与其他图形又有什么联系，却并未让学生自己思考过，那么这个数学问题的生长点就可谓未关注好，让学生一开始就不会运用，而让他们去解决类似问题，这怎么能实现？故在教学的过程中，要注重对基本模型进行深入研究、变式，这样学生才会将一类问题理解透彻，逐渐让这个问题生长起来，解决更多的问题.

2.关注自主的发现学习.

任何一个常见模型都有其研究的必要，这类模型的选取可以中考题为主，也可以教材中的模型为主，教师在课前要进行充分研究，上课时让学生大胆提出自己的想法，每个学生都会有自己的想法，这样不仅可以把问题研究得更透彻，还能提高学生学习数学的积极性，渐渐进入一个良性循环的状态.

弗莱登塔尔曾说过：学习数学唯一正确的方法是实行“再创造”，也就是由学生本人把要学的东西自己发现或创造出来.故教师要善于寻找这些能挖掘、能研究的生长点，让学生去发现、去研究，实现高效课堂.

*本文系南京市教育科学“十二五”规划立项课题“‘跑班’分层模式下初中数学课堂教学与考试评价研究”（课题编号：L/2015/ 181）的阶段性成果.