基于LCD降噪与LS-SVM的滚动轴承故障诊断方法

边兵兵

(平顶山工业职业技术学院，河南 平顶山 467001)

基于LCD降噪与LS-SVM的滚动轴承故障诊断方法

边兵兵

(平顶山工业职业技术学院，河南 平顶山 467001)

在实际工况下滚动轴承较易发生故障，为了保障机械运行可靠性，对其进行故障诊断研究显得非常重要，提出一种基于局部特征尺度分解(Local Characteristic-scale Decomposition, LCD)降噪与最小二乘支持向量机(Least Squares Support Veotor Machine, LS-SVM)的滚动轴承故障诊断方法。首先，利用LCD对轴承信号进行自适应性分解，得到一系列内禀尺度分量(Intrinsic Scale Component, ISC)，然后结合峭度准则筛选出包含主要特征信息的分量，完成信号降噪预处理，并与经验模态分解(Empirical Mode Decomposition, EMD)进行对比，研究LCD算法的优越性；最后提取ISC模糊熵作为信号的敏感特征集，输入到训练好的LS-SVM分类器中进行轴承状态识别。实验研究表明，提出的基于LCD降噪与LS-SVM的轴承故障诊断方法能有效地识别出多种轴承类型，识别率高达84%，是一种行之有效的轴承诊断算法。

滚动轴承；LCD；峭度准则；模糊熵；LS-SVM；故障诊断

0 引言

作为旋转机械设备中极为常见的零件，滚动轴承也是最为常见的故障发生部位，其中大约30%的故障都是由滚动轴承故障导致的[1]。一旦其发生故障，容易导致机械运行受损，严重的甚至威胁到操作人员人身安全。因此，对其进行故障诊断研究是保障机械设备运行可靠性的重要研究内容之一。

在实际工况影响下，采集到的滚动轴承振动信号一般表现出非平稳性、非线性等特点，而故障诊断的难点在于如何有效地提取出信号中的敏感特征。局部特征尺度分解是程军圣等[2]提出的一种新的信号自适应性处理方法，该方法能够有效地将多周期分量信号分解为一组内禀尺度分量之和，非常适用于具有非线性、非平稳性等特点的滚动轴承振动信号时频分析[3]。Chen等[4-5]在样本熵的基础上提出了模糊熵算法，用隶属度函数代替样本熵计算中使用的硬阈值判据，并且在生理电信号领域获得了良好的应用。因此，本文结合LCD算法和模糊熵特征提取算法各自的优点，提取信号的ISC模糊熵敏感特征集，作为LS-SVM分类器的输入特征向量，利用训练好的LS-SVM分类器对轴承所处的状态进行诊断识别研究。

1 故障诊断关键技术

1.1 局部特征尺度分解

局部特征尺度分解能够根据信号本身信息有效地将信号自适应性地分解为一系列ISC之和[2]。使得信号分解具有一定的连贯性，以便有效地提取出信号特征，同时任意两个ISC之间是相互独立的，必须满足以下两个条件：

(1)原始信号任意两个相邻极值点正负性不同；

(2)对于原始信号x(t)的所有极值点(τk,Xk)，k=1,2,…,M，M为极值点个数，其中任意相邻两个极大(小)值点(τk,Xk)和(τk+2,Xk+2)的连线所构成的曲线在横坐标为τk+1的纵坐标：

(1)

须满足Ak+1/Xk+1的比值近似不变。

根据以上ISC分量的定义，LCD对信号的分解步骤如下：

(1)确定原始信号x(t)的所有极值点(τk,Xk)，利用点(τk+1,Ak+1)与点(τk+1,Xk+1)进行线性插值运算，得到基线信号控制点坐标(τk+1,Lk+1)，纵坐标Lk+1=aAk+1+(1-a)Xk+1，其中a为一常数，通常取0.5。如此，任意两个上述极值点通过以上计算，将原始信号分成了若干个区域，现将任意一个区域进行如下线性变换得到：

(2)

将所有划分区域变换得到的Hk按区间标号，由小到大首尾依次相连即得到了基线信号H1(t)。

(2)将H1(t)从原始信号中剥离出来，得到新的信号P1(t)=x(t)-H1(t)，如果P1(t)满足ISC的定义，则有第一个内禀尺度分量ISC1(t) =P1(t)；如果不满足，则以P1(t)作为原始信号重复步骤(1)～(2)，直到满足条件为止。

(3)将ISC1(t)从原始信号中剥离出来，得到剩余信号r1(t) =x(t)-ISC1(t)，继续执行步骤(1)～(2)，得到第二个分量ISC2(t)，如此往复n次，直到rn(t)为单调函数或者小于预测阈值，迭代停止，原始信号被分解为：

(3)

1.2ISC模糊熵特征提取

模糊熵与样本熵一样，都是用来表征时序信号复杂程度，以及信号在多个维数下生成新序列的概率[4]。不同之处在于，模糊熵利用隶属度函数取代了样本熵运算过程中对任意样本间距离的硬阈值判据，这样降低了在熵值计算过程中模糊熵对参数变换的敏感程度，并且模糊熵在运算前对信号进行了均一化处理，消除了信号出现基线漂移的现象。模糊熵计算步骤如下：

(1)将去均值化后的时序信号u1,u2,…,uN重构成一个m维向量，得到一组样本集，新的时序信号如下：

x(i)=[ui,ui+1,…,ui+m-1]，i=1～N-m+1

(4)

(2)计算样本集中任意两个不同样本x(i)和x(j)之间的距离dij：

dij=d[x(i)-x(j)]=max|ui+k-uj+k|

0≤k≤m-1;j,i=1～N-m,j≠i

(5)

(6)

其中，r和n分别为模糊函数边界的宽度(相似容限)和梯度，本文取r=0.15σ(σ为时序列信号的标准差)，n=2。

定义样本的平均相似度φm(r)：

(7)

(4)当重构维数为m+1时，同理可得到φm+1(r)；

(5)原始时序信号的模糊熵定义为：

(8)

1.3 LS-SVM分类算法

考虑到SVM在实际应用中存在的一下问题，引发了学者们对SVM进行改进。Suykens等[8]在SVM的基础上提出了LS-SVM，将二次规划问题转化为求解线性方程组问题，提高了计算效率[9-11]。

已知(xi,yi),i=1,2,…,n;xi∈Rd,yi∈{1,2,…,N}其中，xi为分类器输入样本，n为输入样本个数，yi为输出编号，个数为N，代表识别对象，d为输入样本维数。将输入样本x代入初始化的第m、n类这2类模式分类器中，得到样本对应的分类函数：

(9)

式中，wmn为Lagrange乘子，K(xi,x)为核函数，bmn为设置阈值，s为支持向量的数目。

2 实验装置与数据采集方式

验证实验在模拟实验台上利用加速度振动传感器完成数据采集，实验台的传感器布置如图1所示，在实验中为了模拟出正常、内圈点蚀故障、外圈点蚀故障与滚动体点蚀故障四种状态轴承振动信号，对实验台上的滚动轴承进行更换相应类型齿轮来实现，采样频率设置为10kHz，电机转频设置为45Hz，采集到的四种状态滚动轴承信号时域图如图2所示。

图1 实验台传感器布置图

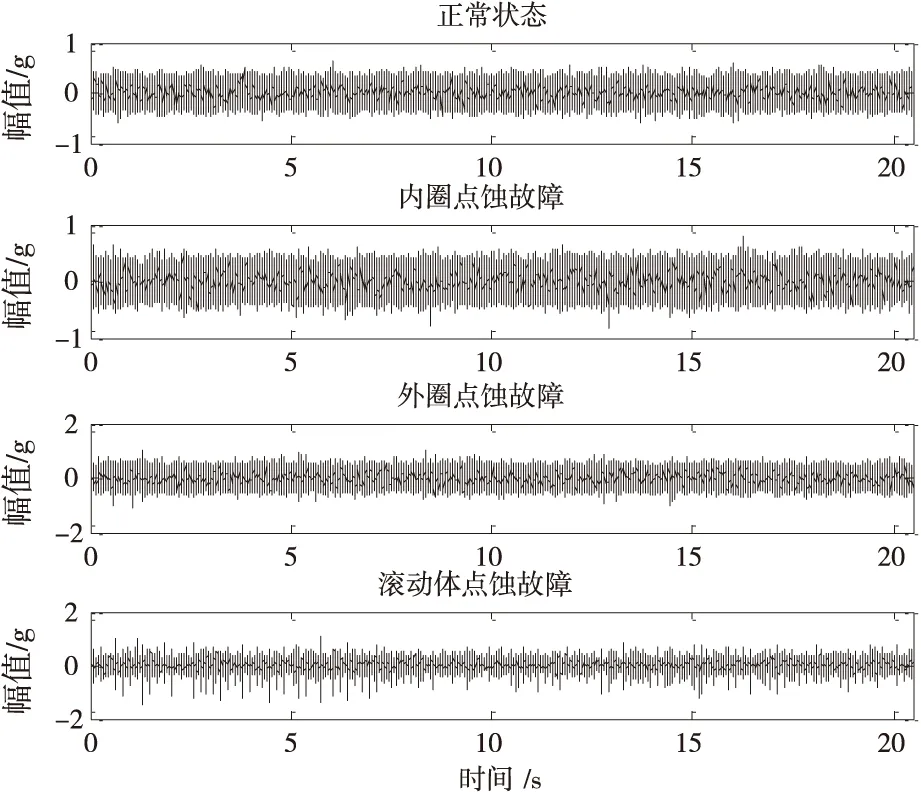
图2 四种状态滚动轴承信号时域图

3 实验与分析

基于LCD降噪和LS-SVM的滚动轴承故障诊断方法流程如图3所示。

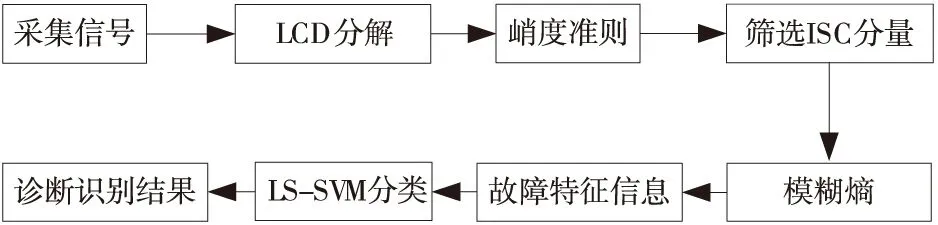
图3 故障诊断识别流程图

下面利用采集到的滚动轴承振动信号对上述诊断算法进行实验验证。考虑到篇幅有限，下面以滚动体点蚀故障为例进行说明。

利用LCD算法对滚动体故障信号进行自适应性分解，一个样本信号的分解结果如图4所示，信号被分解得到4个ISC分量和一个残余量R，分解时间为0.2846s。为了展现LCD算法的优越性，下面对信号进行EMD分解，分解结果如图5所示，得到9个ISC分量和一个残余R，分解时间为0.4395s。对比图4和图5可知，LCD在分解层数和分解效率上明显优于EMD算法，而分解层数越多，这样会加重因多次迭代操作导致端点效应对信号分解结果的影响。

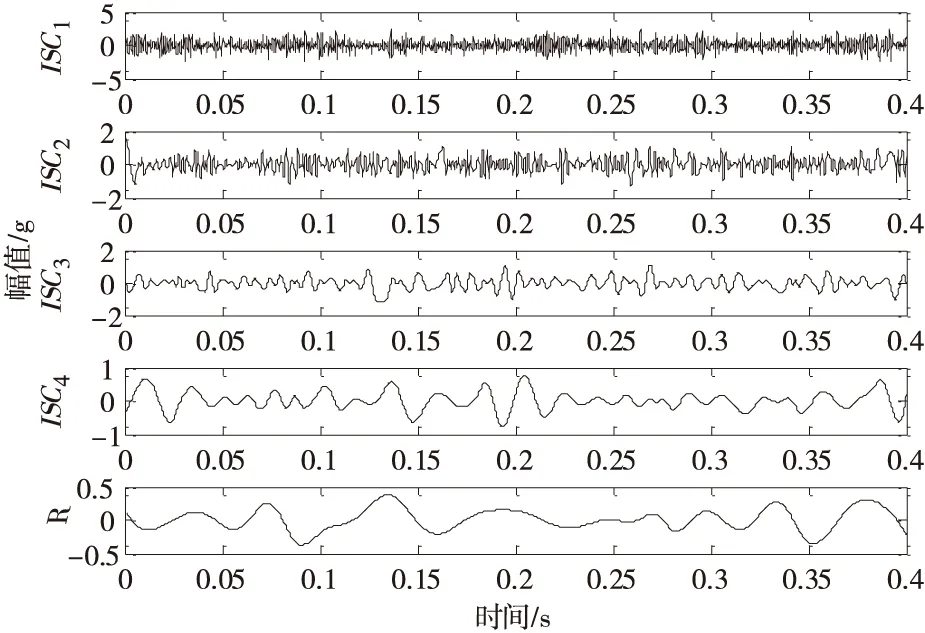
图4 滚动体故障LCD分解结果

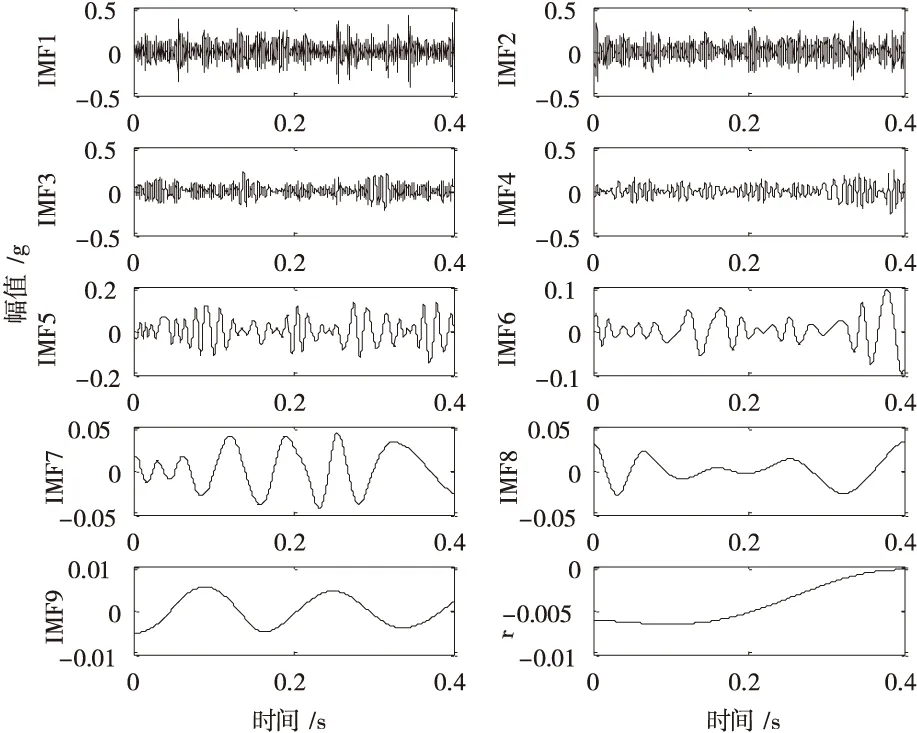
图5 滚动体故障EMD分解结果

[7]可知，正常轴承的振动信号近似服从正态分布，计算信号的峭度系数大约为3，当轴承发生故障时，振动信号会产生幅值较大的脉冲信号，此时含有较多的冲击成分的ISC分量对应的峭度系数将大于3，这就是峭度准则。以此为依据就能筛选出包含主要特征频率的ISC分量，剔除伪分量对后续特征提取的干扰，实现对信号的降噪预处理。下面选择3个滚动体故障样本进行各层ISC峭度系统计算，如表1所示。

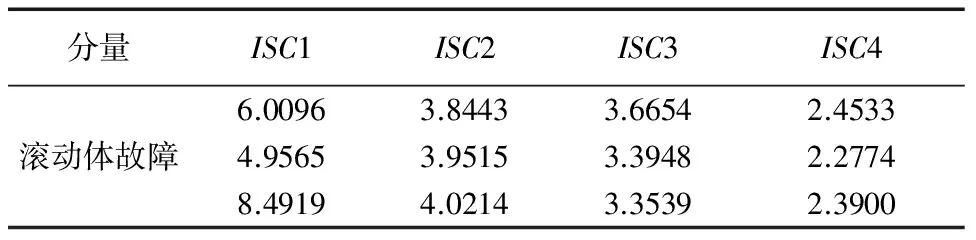
表1 滚动轴承滚动体故障各层ISC峭度系数

根据峭度准则可以筛选出ISC1-ISC3这3层ISC为包含主要特征信息的分量，然后对这3层分量取出ISC模糊熵特征信息，四种类型轴承振动信号的ISC模糊熵如表2所示，正常、内圈和外圈故障的模糊熵主要集中在ISC2，但占比不一样，滚动体故障的模糊熵主要集中在ISC1。

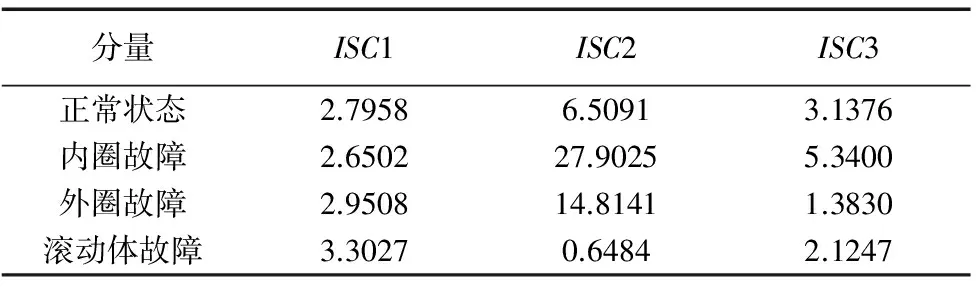
表2 各类状态滚动轴承振动信号ISC模糊熵

下面以LS-SVM为故障分类器，将ISC1-ISC3这3层ISC模糊熵作为特征向量输入，记为X=(x1,x2,x3)，正常、内圈点蚀故障、外圈点蚀故障与滚动体点蚀故障四种状态轴承的输出分别为1、2、3、4。LS-SVM中采用的核函数是径向基函数，这样需要设置的参数只有惩罚参数C和核函数参数σ。在惩罚参数及核函数参数的选择上，我们采用网络搜索法确定C=16，σ=0.25。

将400组轴承类型样本分为300组训练数据，100组测试数据，如图6所示，为实际故障类型与预测类型对比图。实验中，该诊断算法对于四种状态类型滚动轴承的诊断识别率达到84%以上，说明该方法能够有效地诊断识别滚动轴承故障类型。

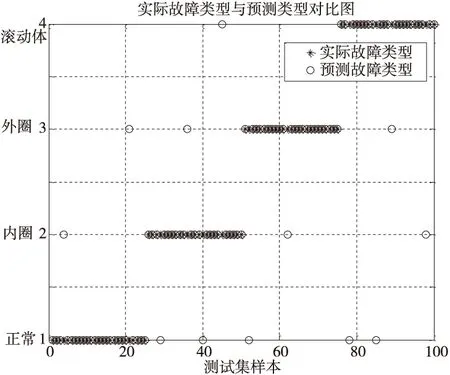
图6 滚动轴承样本的实际故障类型与预测类型对比图

4 结论

实验结果表明，利用基于峭度准则的LCD降噪方法处理滚动轴承振动信号，对比实验得到，从分解效率和分解层数角度出发，LCD相对于EMD算法来说具有明显的优越性，筛选出包含主要特征信息的前3个ISC分量，然后通过求取ISC模糊熵提取故障敏感特征集，结合LS-SVM分类器，能有效的诊断识别滚动轴承故障，识别率达到84%以上，说明此方法时一种有效的滚动轴承故障诊断方法。

[参考文献]

[1] 张沛朋，郭飞燕. 基于PCA-SVM的滚动轴承故障诊断研究[J]. 组合机床与自动化加工技术，2015(11)：88-90.

[2] 程军圣，杨怡，杨宇. 局部特征尺度分解方法及其在齿轮

故障诊断中的应用[J]. 机械工程学报，2012，48(9)：64-71.

[3] 杨宇，曾鸣，程军圣. 局部特征尺度分解方法及其分解能力研究[J]. 振动工程学报，2012，25(5)：602-609.

[4] Chen W, Wang Z, Xie H, et al. Characterization of surface EMG signal based on fuzzy entropy [J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2007, 15(2): 266-272.

[5] Chen WT, Zhuang J, Yu WX, et al. Measuring complexity using FuzzyEn, ApEn, and SampEn [J]. Medical Engineering and Physics, 2009, 31(1): 61-68.

[6] 张前图，房立清，赵玉龙，等. 基于LCD信息熵特征和SVM的机械故障诊断[J]. 机械传动，2015，39(12)：144-148.

[7] 苏文胜，王奉涛，张志新，等. EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J]. 振动与冲击，2010，29(3)：18-21.

[8] Suykens JAK, Vandewalle J. Least squares support vector machine classifiers [J]. Neural Processing Letters, 1999, 9(3): 293-300.

[9] 黄俊，潘宏侠，都衡. 基于EMD近似熵和LSSVM的齿轮箱故障诊断研究[J]. 组合机床与自动化加工技术，2014(3)：111-113.

[10] 钟小凤，贺德强，苗剑. 基于PCA-LSSVM的机车走行部滚动轴承故障诊断研究[J]. 广西大学学报(自然科学版)，2014,39(2)：328-333.

[11] 郭辉，刘贺平，王玲. 最小二乘支持向量机参数选择方法及其应用研究[J]. 系统仿真学报，2006,18(7)：2033-2036.

(编辑 李秀敏)

Fault Diagnosis Method of Rolling Bearing Based on LCD Denoising and LS-SVM

BIAN Bing-bing

(Pingdingshan Industrical College of Technology, Pingdingshan Henan 467001, China)

In actual conditions, the rolling bearing is more prone to failure. In order to guarantee the reliability of mechanical operation, it is very important to study the fault diagnosis of the machine. The fault diagnosis method of rolling bearing based on local characteristic-scale decomposition (LCD) denoising and least squares support vector machine (LS-SVM) is proposed. Firstly, the bearing signal is adaptively decomposed by LCD. A series of intrinsic scale components (ISC) are obtained. Then, combined with the kurtosis criterion used to select mainly contains the characteristic information of the components, the signal denoising preprocessing is completed. Compared with EMD, the superiority of the LCD algorithm is studied. Finally, ISC fuzzy entropy is used as a sensitive signal feature extraction and the input of trained LS-SVM classifier. Experimental results show that the proposed bearing fault diagnosis method based on LCD denoising and LS-SVM can effectively identify a variety of bearing types and the recognition rate is up to 84%. The method is a kind of effective bearing diagnosis algorithm.

rolling bearing; LCD; kurtosis criterion; fuzzy entropy; LS-SVM; fault diagnosis

1001-2265(2017)02-0119-04

10.13462/j.cnki.mmtamt.2017.02.030

2016-04-16；

2016-04-29

边兵兵(1975—)，男，河南平顶山人，平顶山工业职业技术学院讲师，硕士，研究方向为机械设计与制造，(E-mail)649436919@qq.com。

TH162;TG506

A