直流电机无抖动滑模位置控制*

张江华

(常州机电职业技术学院，江苏 常州 213164)

直流电机无抖动滑模位置控制*

张江华

(常州机电职业技术学院，江苏 常州 213164)

针对直流电机伺服系统中普遍存在的参数不确定性以及不确定性非线性等各种扰动，提出了一种基于扰动补偿的无抖动终端滑模位置控制策略，实现了直流电机伺服系统的高精度位置跟踪控制。系统模型考虑了非线性摩擦特性以及外干扰等建模不确定性。所提出的全状态控制器对连续非线性摩擦进行了前馈补偿，进一步改善了系统的低速伺服性能；通过扩张状态观测器对未建模干扰等不确定性进行估计并前馈补偿，提高了系统对外干扰的鲁棒性。同时，所设计的控制器还能保证系统状态在有限时间内趋于平衡状态，提高了系统的快速跟踪性能。最终，通过对比的仿真结果对其进一步工程应用具有实际指导意义。

直流电机；终端滑模；扩张状态观测器；运动控制

0 引言

直流电机伺服系统由于其响应的速度快、传动的效率高以及维护方便等一系列优点，而被广泛地应用于国防、航空航天、民用工业等领域[1-3]。随着这些领域的不断快速发展，对其跟踪性能的要求也越来越高，而系统的性能则与控制器的设计密切相关。直流电机伺服系统是一个典型的不确定以及非线性的系统，在设计控制器的过程中会面临许多建模的不确定性，包括结构不确定性(如随环境、工况等变化的参数不确定性等)以及非结构不确定性(如未建模动态、外部扰动等)，这些存在的不确定性因素可能会使系统期望的控制性能得到严重恶化，导致不理想的控制精度，产生极限环振荡，甚至使所设计的控制器不稳定，从而使控制器的设计变得困难[1]。

针对考虑电机伺服系统中存在的各种不确定性的位置控制策略，学者们进行了大量的研究，主要有反馈线性化[4-5]、自适应鲁棒[3,6-7]以及滑模[8-11]等控制方法。反馈线性化控制方法可以保证系统的高性能，但是其前提是所建立的数学模型必须非常准确，而在实际应用中获取系统的准确数学模型是比较困难的。自适应鲁棒控制方法[12]能够对一类同时存在结构不确定性和非结构不确定性的系统进行有效的控制，然而随着外部干扰的不断增大，其可能会使系统的跟踪性能变差，甚至使整个系统变得不稳定。较强的外干扰意味着较差的跟踪性能，这是非线性自适应鲁棒控制器在实际使用时暴露出来的主要问题。而存在的一些观测器比如扩张状态观测器[13]能够对系统中存在的强干扰予以有效的估计。滑模控制方法对系统中存在的一些不确定性有很强的鲁棒性，其主要包括一般的线性滑模控制[8]和终端滑模控制[9-11]等。但是传统的滑模控制器可能会存在抖动现象，同时终端滑模控制器可能会存在奇异性问题。

本文为解决现有直流电机伺服系统控制中常被忽略的系统建模不确定性、实际使用时存在的高增益反馈及基于传统的滑模控制器存在抖动现象的问题，建立了包含连续静态摩擦模型的非线性系统模型，提出一种基于扰动补偿的直流电机伺服系统无抖动滑模位置控制策略。本文将利用扩张状态观测器对直流电机伺服系统中可能存在的大的扰动进行实时地估计，并在设计控制器的过程中利用这些估计的扰动值进行补偿。所提出的控制方法为全状态反馈控制且其控制电压连续，十分有利于在工程实际中得到应用。对比的仿真结果验证了本文所提出控制策略的有效性和先进性。

1 直流电机伺服系统非线性数学模型

在建立直流电机伺服系统非线性模型时，主要有考虑系统的电气动态和不考虑系统的电气动态两种形式。当直流电机伺服系统中的驱动器内固化的电流环控制器动态过程比较慢时，则基于考虑系统的电气动态的模型会更加有效，反之则不需要考虑系统的电气动态[14]。实际应用的电机，其电气过程大多相当快，所以不需要考虑系统的电气动态，若考虑反而使得控制器设计变得困难同时其控制性能也未必能得到有效的提高。因此，根据牛顿第二定律，建立直流旋转电机位置伺服系统(如图1所示)的运动学方程如下：

(1)

图1 直流电机伺服系统

本文选取如下所示的连续静态摩擦模型为[2]：

(2)

y=x1

(3)

式中，θ1=kf/J，θ2=B/J，θ3=l1/J，θ4=l2/J，η(t,x)=d(t,x)/J，并且参数θ1、θ2、θ3、θ4均为已知的名义值，所有参数偏差造成的不确定性影响都可以归结到系统中总的干扰η(t,x)中。

2 基于扰动补偿的滑模控制器设计

控制器设计的目标是使直流旋转电机伺服系统的位置输出x1尽可能准确地跟踪期望跟踪的位置指令x1d，同时对系统存在的总干扰η(t,x)具有良好的鲁棒性。

2.1 设计扩张状态观测器估计扰动

(4)

根据扩张后的状态方程(4)，设计扩张状态观测器为[15]：

(5)

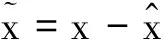
(6)

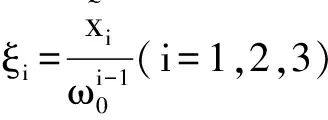
(7)

根据矩阵W的定义可知其满足赫尔维茨准则，因而存在一个正定且对称的矩阵P，使得WTP+PW=-I成立。

引理[16]：若h0(t)有界，则系统的状态及总干扰的估计误差总是有界的并且存在常数δi>0以及有限时间T1>0使得：

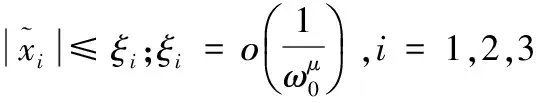
(8)

2.2 控制器设计

选取终端滑模面为：

(9)

式中，s为选取的终端滑模面；c1、c2是常数且其多项式p2+c2p+c1(p为拉普拉斯算子)满足满足赫尔维茨准则，即多项式的所有特征根在复平面的左半平面；α1=α/(2-α)，α2=α，α为常数且α∈(0,1)；e1=x1-x1d为系统的跟踪误差，其中x1d是系统期望跟踪的位置指令，并假设此指令值是关于时间二阶连续可微的；sign(·)为标准符号函数。

(10)

设计的基于扰动补偿的电机伺服系统无抖动滑模控制器如下：

(11)

2.3 稳定性证明

基于非线性直流电机伺服系统所设计的基于扰动补偿的无抖动终端滑模位置控制器将会使系统状态在有限时间内以指数收敛速率到达滑模面s=0，然后将会沿着滑模面s=0在有限时间内趋于平衡状态。

根据控制理论中系统的稳定性分析[17-19]，选取李亚普诺夫方程为：

(12)

运用李亚普诺夫稳定性理论进行稳定性证明，对式(12)求导，并将公式(10)、公式(11)带入求导后的李亚普诺夫方程可得：

(13)

(14)

由于0<ρ<1，1<1/[ρ+(1-ρ)e-φ|s|γ]<1/ρ，因此可得：

(15)

当系统状态到达终端滑模面s时，则：

(16)

因此，系统的跟踪误差将会在有限时间内趋于零，从而使系统状态沿着滑模面s=0在有限时间内趋于平衡状态[17-21]。

所提出的直流电机位置伺服系统非线性控制原理及流程如图2所示。

图2 电机伺服系统非线性控制原理及流程图

3 仿真验证

直流电机伺服系统参数为：惯性负载参数J=0.05kg·m2；力矩放大系数kf=5N·m/V；粘性摩擦系数B=4N·m·s/rad；连续摩擦模型参数q1=750，q2=20，q3=2，l1=0.15，l2=0.1。为了验证系统在所设计的控制器作用下对外干扰的鲁棒性，扰动d(t)=2sin(2πt)(1-e-0.1t3)N·m，为了防止刚开始加入扰动之后产生冲击作用，因此对扰动进行了光滑处理；系统期望跟踪的位置指令为曲线x1d=sin(πt)(1-e-0.1t3)rad，采用这样的指令是确保其足够光滑。仿真采样步长为0.2ms。

本文将基于以下两种控制器针对所建立的直流电机伺服系统非线性数学模型进行仿真对比。

(1)DCTSM：这是本文所设计的基于扰动补偿的终端滑模位置控制器，经过不断反复调试，其控制器参数选取为ω0=480，α=9/16，c1=10，c2=7，E=50，ρ=0.8，φ=2，γ=2。

(2)PID：这是Proportion Integration Differentiation(比例积分微分)控制器[22]。其中PID控制器参数的选取步骤是：首先把比例增益凑试好，直到过渡过程基本稳定，然后再调节积分增益消除余差，最后通过调节微分增益进一步提高控制效果。经过不断反复调试，其控制器参数选取为比例增益kp=1000，积分增益ki=200，微分增益kd=1。

图3 DCTSM控制器作用下系统的跟踪性能以及 DCTSM和PID控制器分别作用下系统的 跟踪误差曲线

图4 扩张状态观测器对总干扰d(t) 的估计值以及其估计误差曲线

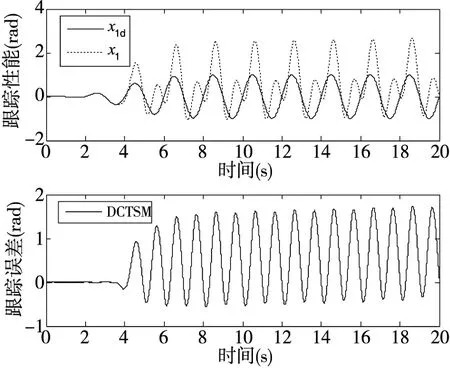
图5 ω0为0时DCTSM控制器作用下系统 的跟踪性能以及跟踪误差曲线

图3中上图表示本文所设计的DCTSM控制器作用下其位置输出跟踪期望位置指令的曲线，下图表示DCTSM和PID控制器分别作用下系统的跟踪误差随时间变化的曲线。从图中可以明显地看出，PID控制器作用下系统的最大稳态跟踪误差为3×10-3左右而DCTSM控制器作用下系统的稳态跟踪误差几乎为0，本文所设计的DCTSM控制器作用下系统的跟踪误差远远小于PID控制器作用下系统的跟踪误差，大大的提高了系统的跟踪性能，表现出良好的跟踪性能，利于在直流电机伺服系统高精度位置控制场合应用。

图4中上图是扩张状态观测器对系统中的总干扰d(t)的估计值随时间变化的曲线，下图是其估计误差随时间变化的曲线。从图中曲线可以看出其最大跟踪误差为0.1左右，约占总干扰值的5%，从而可得所设计的观测器能够准确地将系统中的大干扰估计出来。由于仿真中使用的是大的高频干扰，因此其估计误差会比小的低频扰动相对大。当把扩张状态观测器的参数ω0置0，也就是在控制器设计时不使用该扩张状态观测器，仿真如图5所示，系统的跟踪性能会变得很差，从这个方面也表明了所设计的扩张状态观测器能有效估计并补偿扰动。

图6是DCTSM控制器作用下直流电机伺服系统的控制输入电压随时间变化的曲线，从图中可以清楚地看出所得到的控制输入信号连续且有界，有利于在工程实际中应用。

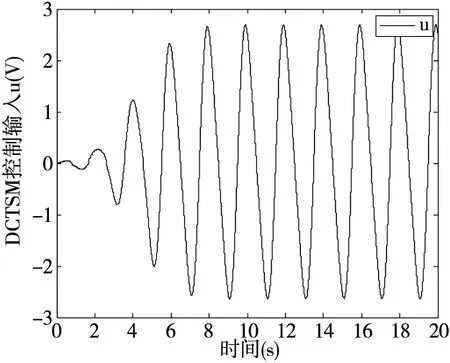
图6 DCTSM控制器作用下系统的控制输入曲线

4 结论

本文针对直流电机伺服系统高精度位置控制设计出了基于扰动补偿的终端滑模位置控制策略。该控制方法通过扩张状态观测器对系统中存在的未建模干扰等不确定性进行估计并前馈补偿，极大地提高了系统对外干扰的鲁棒性。所设计的控制器简单并且其输出电压不会产生抖动及奇异现象，同时该控制器能保证系统状态在有限时间内趋于平衡状态，通过Lyapunov函数证明了整个闭环系统的稳定性。对比仿真结果表明，所提出的控制方法极大地提高了系统的跟踪精度，有利于在工程实际中应用。

[1] Yao J Y, Jiao Z X, Ma D W. Adaptive robust control of DC motors with extended state observer[J]. IEEE Transactions on Industrial Electronics, 2014, 61(7): 3630-3637.

[2] Yao J Y, Yang G C, Jiao Z X, et al. Adaptive robust motion control of direct-drive DC motors with continuous friction compensation[J]. Abstract and Applied Analysis, 2013.

[3] 孙宜标, 刘春丽, 王丽梅,等. 永磁环形力矩电机期望补偿自适应鲁棒控制[J]. 组合机床与自动化加工技术, 2012 (6): 71-74.

[4] Chiasson J. A new approach to dynamic feedback linearization control of an induction motor [J]. IEEE Transactions on Automatic Control, 1998, 43(3): 391-397.

[5] Boukas T K, Habetler T G. High-performance induction motor speed control using exact feedback linearization with state and state derivative feedback[J]. IEEE Transactions on Power Electronics, 2004, 19(4):1022-1028.

[6] Xu L, Yao B. Adaptive robust precision motion control of linear motors with negligible electrical dynamics: theory and experiments[J]. IEEE/ASME Transactions on Mechatronics, 2001, 6(4): 444-452.

[7] Lu L, Yao B, Wang Q, et al. Adaptive robust control of linear motors with dynamic friction compensation using modified LuGre model[J]. Automatica, 2009, 45(12): 2890-2896.

[8] RamanARAYANAN V, Sabanovic A, Cuk S. Sliding-mode control of brushless dc motor[J]. Journal of the Indian Institute of Science, 2013, 67(7&8): 279.

[9] Wu Y Q, Yu X H, Man Z H. Terminal sliding mode control design for uncertain dynamic systems[J]. Systems & Control Letters, 1998, 34(5): 281-287.

[10] Feng Y, Yu X H, Man Z H. Non-singular terminal sliding mode control of rigid manipulators[J]. Automatica, 2002, 38(12), 2159-2167.

[11] Feng Y, Han F L, Yu X H. Chattering free full-order sliding-mode control[J]. Automatica, 2014, 50(4): 1310-1314.

[12] Yao B, Tomizuka M. Adaptive robust control SISO nonlinear systems in a semi-strict feedback form[J]. Automatica, 1997, 33(5): 893-900.

[13] Han J Q. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900-906.

[14] 何洪军, 张东宁, 马传宝. 机械手臂重复定位精度和运动速度测量实验研究[J]. 微特电机, 2016, 44(3): 35-37.

[15] Gao Z Q. Scaling and bandwidth-parameterization based control tuning[C]. In Proceedings of the American Control Conference, 2006, 6: 4989-4996.

[16] Zheng Q, Gao L, Gao Z Q. On stability analysis of active disturbance rejection control for nonlinear time-varying plants with unknown dynamics[C]. In Proceedings of the 48th IEEE Conference on Decision Control, 2007: 3501-3506.

[17] Drakunov S V, Utkin V I. Sliding mode control in dynamic systems[J]. International Journal of Control, 1992, 55(4): 1029-1037.

[18] Edwards C, Spurgeon S. Sliding mode control: theory and applications[M]. CRC Press, 1998.

[19] Utkin V, Guldner J, Shi J. Sliding mode control in electro-mechanical systems[M]. CRC press, 2009.

[20] Bartolini G, Ferrara A, Usani E. Chattering avoidance by second-order sliding mode control[J]. IEEE Transactions on Automatic Control, 1998, 43(2): 241-246.

[21] Drakunov S V, Utkin V I. Sliding mode control in dynamic systems[J]. International Journal of Control, 1992, 55(4): 1029-1037.

[22] Silva G J, Datta A, Bhattacharyya S P. New results on the synthesis of PID controllers[J]. IEEE Transactions on Automatic Control, 2002, 47(2): 241-252.

(编辑 李秀敏)

Free Chattering Sliding Mode Motion Control for DC Motors

ZHANG Jiang-hua

(Changzhou Institute of Mechatronic Technology, Changzhou Jiangsu 213164, China)

For all kinds of disturbances existing in DC motor servo systems such as parametric uncertainties and uncertain nonlinearities and so on, we propose a disturbance compensation based free chattering terminal sliding mode control strategy which implements high-precision position tracking control of DC motors. The established system model takes nonlinear friction characteristics and modeling uncertainties as well as external disturbances of the system into account. The proposed full state controller feedforward compensates the nonlinear continuous friction and further improves low-speed servo performance of the system. By utilizing an extended state observer to estimate the model uncertainties as well as external disturbances and feedforward compensating it, the robustness of the system to external disturbances has been improved. At the same time, the presented controller can guarantee the system state converge to the equilibrium state in a finite time, which improves the fast tracking performance of the system. Eventually, comparing simulation results do have practical guiding significance to the further engineering application.

DC motors; terminal sliding mode; extended state observer; motion control

1001-2265(2017)02-0089-05

10.13462/j.cnki.mmtamt.2017.02.022

2016-10-13；

2016-11-11

国家自然科学基金科研资助项目(51675279)

张江华(1973—)，男，浙江东阳人，常州机电职业技术学院副教授，硕士，研究方向为机-电-液伺服控制，非线性控制，(E-mail)zhj88000@163.com。

TH166;TG506

A