车削工艺参数的智能生成及应用*

刘 岩，段国林，蔡 瑾

(河北工业大学 机械工程学院，天津 300131)

车削工艺参数的智能生成及应用*

刘 岩，段国林，蔡 瑾

(河北工业大学 机械工程学院，天津 300131)

为了能够快速而准确地选择加工参数，并且保证产品的加工质量，提出了基于BP网络模型的车削参数智能选择方法。应用正交试验获取影响加工表面粗糙度的切削参数如吃刀量、进给量、转速和刀具圆角大小各因素的映射关系，建立不同加工阶段的切削数据库。通过BP网络模型学习和训练，不仅能智能的选择加工参数，而且能够划分产品加工阶段。将试验数据和BP网络预测的数据进行回归分析，验证了BP模型的实用性。

正交试验；切削参数；车削加工；BP网络；回归分析

0 引言

工艺参数的选择在产品加工制造过程中起着非常重要的作用，具有复杂性和不确定性，国内外很多研究人员通过智能算法如神经网络、模糊集、遗传算法等建立了粗糙度和工艺参数的映射关系模型，可以快速、准确和智能地选择工艺参数[1]。刘伟强等建立了基于BP神经网络磨削工艺参数的预测模型，从工件材料、砂轮材料和加工条件三方面考虑，优化磨削加工参数[2]。吴明以凸轮轴数控磨削工序为例，采用人工神经网络构建加工参数和加工精度之间的映射模型，从而优化工艺参数[3]。赵昌龙等在并联机床加工过程中，建立神经网络模型预测研抛加工的表面粗糙度，并对神经网络算法进行了改进，提高预测精度[4]。朱红雨等利用神经网络建立了铣削力、铣削温度和表面粗糙度的预测模型，运用遗传算法得到最佳的工艺参数组合[5]。Kant等应用人工神经网络建立产品表面粗糙度的预测模型，以最小粗糙度为目标，使用遗传算法优化加工参数。

本文采用正交试验获取样本数据，分析车削加工过程中的工艺参数对粗糙度的影响。在产品加工过程中为了要达到设计要求，同一个特征需要不同的加工操作阶段才能完成。根据加工要求粗糙度的大小，建立了加工阶段判断程序，能够分类加工阶段。同时通过建立不同加工阶段的切削数据库，使BP网络模型的参数选择更加准确并且符合实际生产需求。

1 加工粗糙度影响因素分析

采用多因素正交试验分析工艺参数对粗糙度的影响,减少试验次数并得到最优参数组合。

1.1 实验条件

工件材料：直径为160mm长度为300mm的毛坯棒料，材料类型为45号钢。试验设备：数控机床型号CKA6163。检测仪器:材料硬度测量仪器是上海思为便携式里氏硬度计TH120，测得工件硬度为HB155。测量表面粗糙度仪器是德国Mahr MarSurf PS1便携式表面粗糙度仪。刀具选择:刀架型号MCLNR3232P16，主偏角95°。加工方式为车外圆，工件装夹方式为一夹一顶。

1.2 实验设计

刀具圆角、吃刀量、进给量和主轴转速为影响粗糙度结果的主要因素，采用四因素三水平的正交表。数控加工中要求粗加工时刀具圆角大小为0.8，精加工时为0.4，即加工质量好时要求刀具圆角小，所以虚拟一个水平如表1所示。

表1 试验正交表极差分析

1.3 试验结果分析

通过极差分析可以获得每个水平对结果的影响，如图1所示。

由图可知：粗糙度值与刀具圆角大小成反比，即数控车床在粗加工时应选择刀具圆角大的车刀；吃刀量对结果的影响不明显，但随着粗糙度值的增大而加大；在材料、刀具和吃刀量确定的情况下，粗糙度值取决于进给量和主轴转速，尤其是主轴转速影响显著，进给量越小，主轴转速越大，得到的粗糙度值越小。所以为了获得较高的加工质量(精加工)时需要降低进给量和吃刀量的值而选择较高的主轴转速。

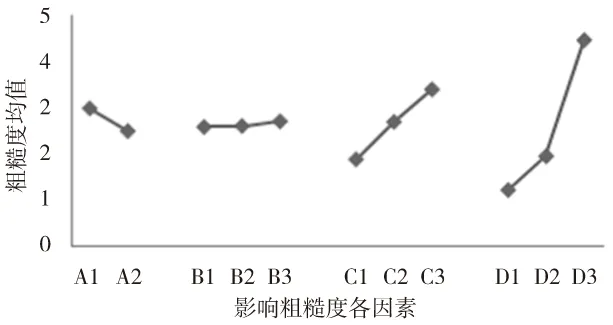
图1 各因素对粗糙度的影响关系图

1.4 切削参数数据库

1.4.1 粗糙度表达式的推导

通过分析试验得到的数据，采用曲线拟合的方法得到测量结果和各因素的映射关系表达式：

(1)

其中，K为常量，abcd分别为对apfvrc的影响指数。由于各个因素与结果是非线性关系，需要对关系式两边取对数，

lgRa=lgK+algap+blgf+clgv+dlgrc

(2)

令lgRa=y，lgK=k，lgap=x1，lgf=x2，lgv=x3，lgrc=x4，转换为线性函数：

y=k+ax1+bx2+cx3+dx4

(3)

需要先将表2中主轴转速数据由公式(4)进行n-v转换：

(4)

式中，D为工件待加工表面的直径(mm)，然后将所有数据经过对数处理，代入式(3)建立多元线性回归方程组，采用文献[7]的回归分析和线性最小二乘法，可以得到粗糙度和工艺参数之间的映射表达式：

(5)

1.4.2 切削参数数据库的建立

零件的加工分段可以划分为：粗加工、半精加工、精加工、细加工和超精加工五部分[8]。据切削加工手册选取切削参数并应用表达式(5)计算粗糙度值，建立切削参数数据库。以粗加工为例，应用MATLAB编制程序，切削参数数据库的建立过程如下：

step1：随机生成(0-1)间m行3列的矩阵，X=rand(m,3)，m为切削参数的个数,X1=X(:,1),X2=X(:,2),X3=X(:,3)，X1、X2、X3分别为吃刀量ap进给量f切削速度v归一化的值；

step2：根据金属切削手册中数控车床的参数范围[9]分别设置粗车的极值；

step4：输入刀具圆角rc值，代入式(5)得到零件加工粗糙度值XX4，并保留小数点后两位；

step5：由ACCESS建立车削粗加工的切削参数数据库，加工阶段名称为关键字。

程序建立的切削数据库包含6个属性：

P=[加工阶段名称，加工标识，吃刀量，进给量，切削速度，粗糙度值]

同理，可以得到其他4组加工阶段的切削参数表，由关键字联接各个加工阶段，应用ACCESS系统建立并管理车削参数的数据库。

2 样本数据处理

为了取消各维数据间不同量级的差异，输入数据和输出数据需要进行归一化处理。吃刀量、进给量和切削速度三个变量采用离差标准化法转换为0～1区间的数值。

2.1 输入数据处理

工艺参数的选择与加工材料、机床、刀具等加工条件有关，所以在加工机床一定的条件下，设置输入数据为材料类型、材料硬度、刀具圆角和用户要求Ra四个变量。X1材料类型：有色金属为0，钢件为0.5，铸铁为1。X2材料硬度：HB<180为0，经过调质处理硬度HB180-250为0.5，由淬火处理硬度较高的HRC40-50为1。X3刀具信息：根据数控机床常用设置刀具圆角大小为0.4mm为0，0.8mm为1。X4表面粗糙度要求：一般数控机床的加工范围为12.5～0.4(μm)，将零件图纸常标注的粗糙度值，根据式(6)转换结果如表2所示。

本组收治的30例产后出血产妇经临床护理干预后,均得到有效控制,伤口愈合满意,子宫复旧好,并康复出院,且无并发症。

X4=(log12.5-logRa)/(log12.5-log0.4) (6)

根据粗糙度值将零件加工划分5个阶段：[12.5～6.3]粗加工1阶段，取值范围(0～0.2)；[6.3～3.2]半精加工2阶段，取值范围(0.2～0.4)；[3.2～1.6]精加工3阶段，取值范围(0.4～0.6)；[1.6～0.8]细加工4阶段，取值范围(0.6～0.8)；[0.8～0.4]超精加工5阶段，取值范围(0.8～1)。

2.2 输出数据处理

输出参数根据机床的加工能力和工艺手册可得参数的变化范围如下所示，并对其进行离差标准化线性转换。设置车削参数范围为吃刀量ap：0.3～5mm；进给量f:0.08～0.4mm/r；切削速度v:50～260m/min。

2.3 加工阶段划分程序

加工阶段是依次由粗到精加工的过程，输入粗糙度的值可以判断出需要的几个加工阶段及该阶段的加工参数，该判定过程如图2所示。

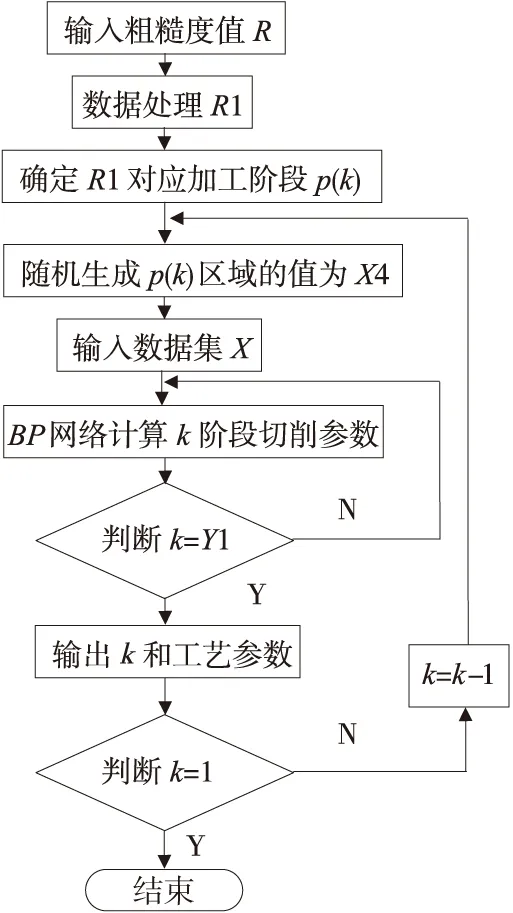
图2 加工阶段判断流程图

输出数据的第一位为加工阶段标识(i=1,2…5)，引入加工阶段标识的目的是为了防止出现吃刀量很大，切削速度又很高的不符合加工规则的现象，进一步保证了生成的工艺参数符合实际加工需求。输出工艺参数还需要判断是否与输入值X4属于同一个加工阶段，保证输出的参数合理性。加工阶段判断过程步骤如下：

step1：输入粗糙度的值R，对其进行归一化数据处理得到数值R1；

step2：确定R1所在的加工阶段P(k)=k(k=1,2,3,4,5)；

step3：随机生成该加工阶段内的数值X4，存入输入数据，生成数据集合X；

step4：由BP网络计算切削参数；

step5：提取输出参数Y中的第一列数据Y1，判断Y1=k;如果两者相等则继续，否则BP重新计算工艺参数；

step6：判断k值，如果k≠1，则k=k-1, 并在此区域内随机产生数值X4，生成输入数据集，由BP网络计算切削参数, 重复step3～step5；

step7：重复step6，直至k=1,程序结束。

3 BP神经网络

BP神经网络可以并行处理非线性的大量参数，是一种多层的前馈神经网络，输入数据前向传递，误差反向传播[10]。而且不需要建立数学优化模型，可以在信息不完全，通过预测误差调整网络权值和阈值，使网络预测输出和期望输出相接近。应用BP预测加工参数可以并行处理切削要素三者间的关系，将工艺参数选择的相关专业知识通过网络训练，使其能够智能输出加工所需要的参数。

3.1 网络拓扑结构

零件加工参数的BP网络拓扑结构为三层，输入层为四个神经元，影响工艺参数的因素Xi(i=1,2,3,4)，输出层是加工阶段标识和切削三要素四个神经元Yj(j=1,2,3,4)，输出数据第一列为加工阶段的标识。隐含层神经个数确定为9个，网络拓扑结构为4-9-4。隐含层传递函数为tansig，输出层传递函数purelin 。

3.2 网络学习和训练

根据车削参数数据库程序可生成不同加工阶段的5组切削数据库，每组随机生成20个数据集，将其合并为100个数据集合，用于网络的学习和训练。设置BP网络参数：训练函数为Levenberg-Marquart(LM)，该优化算法是训练函数中最快的反向传播算法，但是需要的内存比其他算法大。学习函数learngdm梯度下降学习法，训练目标0.001；学习率0.1。

3.3 预测结果及分析

补充最佳组合试验D1C1A2B1等共6组数据如表3所示，用于验证上述的BP网络预测模型的准确性。仿真工艺参数经过反归一化处理，得到参数预测结果如表4所示。通过加工标识验证预测的加工参数符合该加工阶段的参数取值范围，可以将该组数据输入切削参数数据库。

表3 验证数据表

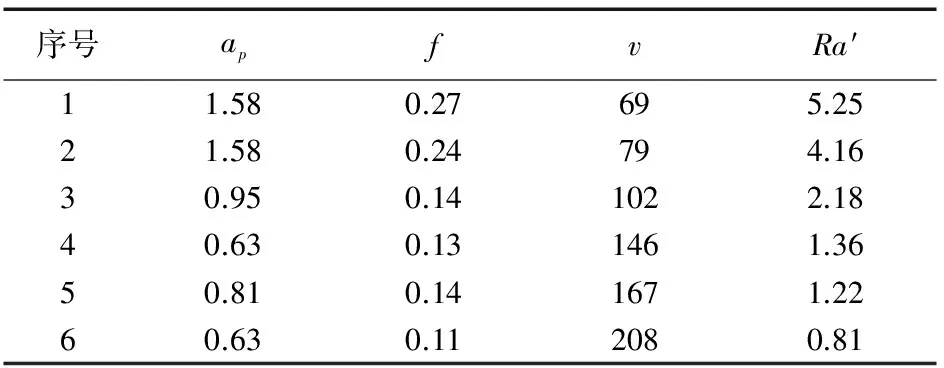
表4 BP仿真工艺参数表

将试验得到的粗糙度值与仿真工艺参数代入式(5)得到的粗糙度值做回归分析，如图3所示，相关系数R=0.9926，则BP模型的预测结果是正确的。

图3 回归分析图

4 实例

锤式破碎机的固定板零件，如图4所示。通过螺栓联接大皮带轮和传动轴，其功能为轴向定位。零件的左侧端面粗糙度为6.3μm，材料为45号钢，以该端面加工特征为例，通过BP网络模型预测加工参数。为了满足加工要求，粗糙度值在(0.2,0.4)范围内随机生成数R1=0.28。网络输入数据X=[0.5,0,0,0.28]，输出数据经过反归一化处理得到的加工参数为半精加工[2, 2, 0.3, 81]；粗加工[1, 3.2, 0.35, 53]，代入粗糙度表达式(5)得到各加工阶段的粗糙度值分别为4.7μm和8.3μm，最终加工结果4.7μm小于6.3μm满足生产要求。

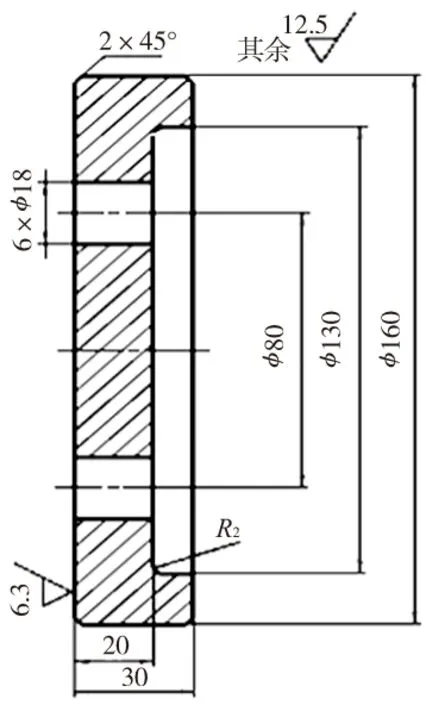
图4 固定板零件图

5 结论

(1)本文通过正交试验，分析试验结果和各因素的相互关系，由极差分析得到影响粗糙度的各因素优先顺序，并获得到最佳的参数组合，得到机床主轴转速对结果影响最大，其次是进给量和刀具圆角大小，而吃刀量对结果影响最小。

(2)通过BP神经网络建立智能的选择工艺参数模型，由上述试验得到的数据推导出粗糙度和切削三要素及刀具圆角的映射关系式，生成不同加工阶段的切削数据，用于网络学习和训练。

(3)将网络智能选择的参数带入表达式得到的粗糙度，与试验的粗糙度进行回归分析，验证BP模型。通过回归分析可以得到两者的相关系数为0.9926，证明了该方法的有效性。

(4)该网络模型不仅可以智能的选择切削参数，而且可以根据输入值粗糙度的大小判断加工阶段，确定零件特征的加工操作阶段及其各个阶段的切削参数，使其符合实际加工需求。

[1] Chandrasekaran M, Muralidhar M, Murali Krishna C, et al.Application of Soft Computing Techniques in Machining Performance Prediction and Optimization: a Literature review[J]. International Journal of Advanced Manufacturing technology,2010,46(5):445-464.

[2] 刘伟强,杨建国. 基于神经网络的磨削工艺参数智能预测模型[J]. 组合机床与自动化加工技术,2013(8):91-94.

[3] 吴明.基于BP神经网络的汽车发动机凸轮轴数控磨削加工工艺优化[J].湖南理工学院学报(自然科学版),2013,26(4):36-39.

[4] 赵昌龙，于淼.基于神经网络的并联机床表面粗糙度预测[J].机床与液压,2015,43(11):46-48.

[5] 朱红雨，李迎.基于神经网络和遗传算法的高速铣削工艺参数优化的研究[J].工具技术,2007,41(12):29-32.

[6] Kant G, Sangwan K S.Predictive Modelling and Optimization of Machining Parameters to Minimize Surface Roughness using Artificial Neural Network Coupled with Genetic Algorithm[C].15th CIRP Conference on Modelling of Machining Operations,2015, 31:453-458.

[7] 张洪潮,孔露露,李涛，等.切削比能模型的建立及参数影响分析[J]. 中国机械工程,2015,26(8):1098-1104.

[8] 田颖,江平宇，周光辉，等.基于蚁群算法的零件多工艺路线决策方法研究[J].计算机集成制造系统,2006,12(6):882-887.

[9] 张益芳. 金属切削手册[M].上海:上海科学技术出版社，2011.

[10] 王小川，史峰，郁磊，等. MATLAB 神经网络43个案例分析[M].北京:北京航空航天大学出版社，2013.

(编辑 李秀敏)

Intelligent Generation and its Application of Cutting Parameters

LIU Yan, DUAN Guo-lin, CAI Jin

(School of Mechanical Engineering,Hebei University of Technology, Tianjin 300130,China)

In order to select cutting parameters quickly and accurately and ensure processing quality of products, an intelligent selection method of cutting parameters based on BP neural network model is proposed. Process parameters such as cutting depth, feed, spindle speed and tool fillet size effect surface roughness by using orthognal experiment. Different processing stages of the cutting parameter databases are created based on test data. BP neural networks modle can not only choose the processing parameters intelligently, but divide processing stages by learning and training fuctions. The test data and BP network prediction data regression analysis is to verify the practicality of BP model.

orthogonal experiment; cutting parameter; turning process; BP neural networks; regression analysis

1001-2265(2017)02-0157-04

10.13462/j.cnki.mmtamt.2017.02.041

2016-06-19；

2016-07-24

河北省自然科学基金项目(E2010000052)

刘岩(1977—)，女，辽宁葫芦岛人，河北工业大学博士研究生，研究方向为CAD/CAPP/CAM，(E-mail)lyan092012400900@sina.com。

TH162;TG506

A