基于多特征与MSVM的动态过程异常监控*

刘玉敏，赵哲耘

(郑州大学 商学院，郑州 450001)

基于多特征与MSVM的动态过程异常监控*

刘玉敏，赵哲耘

(郑州大学 商学院，郑州 450001)

为了提高动态过程异常模式的监控效率和精度，将动态过程质量模式的统计特征和小波变换低频近似系数作为分类特征的方法，并通过支持向量机构建多分类识别模型。首先提取出动态数据流的均值特征，将六种质量模式划分为正常与周期模式、向上模式、向下模式三大类；接着采用均方幅值特征和斜率特征将正常与周期模式进行细分；最后利用低频系数对向上模式和向下模式进行进一步识别。仿真实验表明，所提模型兼顾识别精度与计算效率，是一种有效的动态过程异常监控方法。

动态过程；质量异常模式；小波变换；统计特征；支持向量机

0 引言

生产制造过程具有时变性、高噪声、非平稳等特点，由于受到过程中人、机、料、法、环、测等因素的影响，极易产生异常波动。当传感器采集到的数据流呈现出异常变化趋势时，通常表明加工状态存在潜在问题。对生产过程进行有效的监控，及时发现并消除造成生产过程中的质量异常波动的因素，是确保产品质量、降低企业质量成本的关键。因此，如何提高智能监控方法对于质量异常模式的识别精度，成为了质量异常监控的核心问题[1]。

由于连续性、非线性、动态性的生产过程产生的数据流具有高维度、高噪声等特点，对质量异常模式识别方法的研究主要集中在基于特征提取的质量异常模式识别方面[2-4]。例如，Hassan[5]使用6种统计特征对质量异常模式进行识别，该方法兼顾了识别精度和效率；吴少雄[6]利用一维离散小波变换，而后采用概率神经网络建立了异常识别模型；Vahid等人[7]将统计特征与形状特征进行混合，建立了多分类支持向量机(MSVM)模型，并取得了较高的识别精度。综上所述，当前基于特征提取的方法主要通过单一数据特征或多特征混合与分类器相结合。然而，由于不同质量模式间具有不同的分类特征，单一类特征会造成信息的缺失；多特征混合会增加分类特征维度从而降低模型的识别效率。如何根据不同质量模式的特点提取维度低、表征能力强的特征并构建高效的识别模型成为了动态过程异常监控的关键。本文提出了一种基于小波变换与统计特征相结合的MSVM动态过程异常监控方法。首先利用均值特征将六种质量模式分为三大类。继而，分别通过统计特征提取和小波变换对数据流的模式进行进一步识别，并使用粒子群算法对SVM进行优化，建立基于多特征与MSVM的识别模型。仿真实验表明，本文所提模型能够有效提高识别精度并减少计算量。

1 动态过程质量模式分类

在生产过程中，动态过程由于受到偶然因素和异常因素的影响，其质量特性值的波动也呈不同的变化形态。其中，偶然影响下的质量特性值在目标值上下随机波动如图1a所示，其动态过程运行状态当属于正常模式(Normal pattern,NOR)。当生产加工过程受到异常因素影响时，动态数据流呈现上升趋势(Increasing Trend, IT)、下降趋势(Decreasing Trend, DT)、向上阶跃(Upward Shift, US)、向下阶跃(Downward Shift, DS)和周期模式(Cycle, CYC)，6种质量模式如图1所示。

图1 动态过程质量模式

由于实际生产过程中的数据难以批量获取，因此根据其他学者的研究经验，本文采用Monte Carlo方法生成所需要的样本数据，公式如下：

x(t)=μ+γ×σ+d(t),t=1,2,…,n

(1)

式中，x(t)为t时刻下质量特性值；μ为质量特性目标值；σ为过程标准差；γ为随机因素造成的波动，通常为服从(0,σ2)的高斯白噪声，在此令γ～N(0,1)，d(t)为异常因素导致的波动。为了简化仿真实验，通常取μ=0，正常、周期、趋势和阶跃模式的仿真见式(2)～式(5)：

x(t)=μ+γ×σ

(2)

x(t)=μ+γ×σ+Asin(2πt/T)

(3)

x(t)=μ+γ×σ±k×t

(4)

x(t)=μ+γ×σ±b×s

(5)

式中：k为趋势变化斜率，在此取k∈[0.2σ,0.4σ]；T为变化周期，通常取T=15或20；A为周期幅度，取A∈[1σ,2.5σ]；s为阶跃幅度，取s∈[1σ,2.5σ]；b为阶跃位置，阶跃前b=0，阶跃后b=1。

2 质量异常模式识别模型

2.1 质量模式统计特征提取

统计数据在刻画动态过程质量模式的基本特征时，可以通过提取不同的统计特征来增加不同模式间的区分度，从而提高分类器对质量异常模式的识别效率和识别精度[8-9]。本文在文献[8-9]的基础上，进一步选取均值、均方幅值和斜率作为特征参与后续的质量异常模式识别。选取的依据是：①该特征能够有效的区分六种动态过程质量模式；②控制所取特征集的维度，降低训练复杂度。依据式(6)～式(8)对动态数据流提取均值特征、均方幅值及斜率特征：

(6)

(7)

(8)

2.2 一维离散小波分解

虽然原始特征对质量模式序列有较为全面的描述，能反映了全局信息，但由于原始数据受到大量的噪声干扰，实用性较差。为凸显数据流的变化信息，将动态数据流进行一维离散小波分解，分别获取高频细节部分和低频近似部分。低频近似系数过滤掉了周期信号和噪声信号，保留了趋势信号和阶跃信号。因此为了使得所提取的特征对趋势模式和阶跃模式间具有更强的区分性，本文对原始数据进行一维离散小波分解。如图2所示。

一维离散小波分解(DiscreteWaveletTransform,DWT)通过低通滤波器h(n)和高通滤波器g(n)，将数据流X(t)分解为高频细节系数和低频近似系数，经过L层变换后，能够有效的刻画数据流变化趋势的信息分布在低频部分，其噪声主要分布在高频细节部分。在第j层上的一维离散小波变换通过正交投影PjX和QjX将Pj-1X分解为：

(9)

(10)

(11)

式(9)～式(11)中，P0X=X，h(n)和g(h)分别为低通与高通权重系数，p为权系数的长度。cAj为低频近似系数，cDj为高频细节系数；N为输入信号长度，L为分解的层数；φ(t)和ψ(t)分别为尺度函数和小波基函数。

图2 一维离散小波分解与重构

3 基于PSO-SVM的识别模型

3.1 分类器构建

支持向量机(SupportVectorMachine，SVM)通过寻求结构风险最小化来提高分类器的泛化能力，并通过核函数将线性不可分的数据映射到高维空间寻找最优分类超平面；SVM在解决小样本、非线性和高维模式识别问题中展现出许多特有的优势，解决了小样本和线性不可分的二分类问题。其分类原理如下：

(12)

s.t.yi(ωTxi+b)≥1-ξi,i=1,2,…,n

(13)

式中:ξi为松弛变量；C为惩罚因子，C越大表明对错误分类的惩罚力度越大。引入核函数k(xi,x)后，可得到SVM的分类函数为：

(14)

由SVM的原理可知，单个的SVM仅能解决二分类问题，对于要识别六种质量异常模式，需要构建多支持向量机模型(MSVM)来实现多分类问题。常用的用于构建MSVM的方法有一对多(One Versus Rest, O-V-R)、一对一(One Versus One，O-V-O)、半对半(Half Against Haft，HAH)、有向无环图等[10]。本文将“一对一”与“半对半”的方法结合起来构建MSVM。SVM中罚函数和核函数参数的选择直接影响到支持向量机分类精度，用支持向量机做分类时，最大的问题就是如何选择模型的参数[11]。由于粒子群算法(Particle Swarm Optimization，PSO)具有无需编码、收敛速度快、操作简单等优点，因此，本文采用粒子群算法对支持向量机的罚函数和函核数参数进行优化，寻找到模型的全局最优解，从而提升分类器的分类性能。本文构建的识别模型如图3所示。

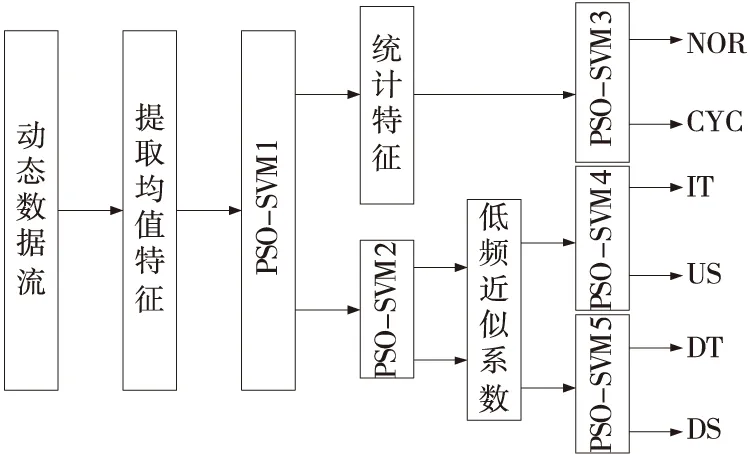
图3 基于PSO-SVM的质量异常模式识别模型

核函数需要满足Mercer条件，常见的核函数包括：

(1)多项式核函数：

K(x,xi)=x·xi

(15)

(2)p阶多项式核函数：

K(x,xi)=[(x·xi)+1]ρ

(16)

(3)多层感知机核函数：

K(x,xi)=tanh[v(x·xi)+c]

(17)

(4)高斯径向基核函数:

(18)

高斯核函数(RadialBasisFunction，RBF)被广泛用于质量诊断中，实验表明，RBF核函数拥有更好的识别精度。因此，本文选用RBF核函数作为SVM中的核函数。

3.2PSO参数寻优

粒子群算法(ParticleSwarmOptimization)是种群智能算法，最初受到飞鸟捕食研究的启发，其原理是通过群体中粒子间的合作与竞争产生的群体智能指导优化搜索。算法中，每个粒子的位置都为待优化问题的一个随机解，并且每个粒子都具有一个适应度，该适应度由目标函数决定。由于目前SVM参数的选择大多还依赖于经验和手动的方法，缺乏指导参数选择的理论支撑，存在盲目性和效率低等问题。故本文通过PSO算法实现SVM的参数自动寻优，如图4所示。即将SVM-RBF的核函数参数g和惩罚因子C作为粒子群算法中的粒子的位置，即Xi=(C,g)，并选取SVM的识别精度作为算法的适应度函数，其表达式为：

(19)

式中，Ctrue和Cfalse分别为分类正确数和分类错误数。

粒子群算法的数学表达为：在n维空间，X={x1,x2,…,xm}为优m个粒子组成的种群，在t时刻，第i个粒子的位置为Xi(t)=(xi1(t),xi2(t),…,xiN(t))，其个体最优位置为Pi(t)=(pi1,pi2,…,piN),其全局最优位置表示为Pg(t)=(pg1,pg2,…,pgN)，则SVM中粒子的速度的更新过程如式(20)：

υij(t+1)=υij(t)+c1rand()[pij(t)-zij(t)]+

c2rand()[pgj(t)-zij(t)]zij(t+1)=zij(t)+υij(t+1)

(20)

式中：υij(t)表示第i个粒子在第t次迭代中第j维上的速度。c1和c2为加速常数，pij和pgj分别为粒子的局部极值和全局极值，rand()为0～1范围内的随机数，zij为第i个粒子在第j维空间上的位置。

图4 SVM参数寻优

4 仿真实验分析

4.1 数据特征提取

很据MonteCarlo公式，对每种模式仿真生成120组仿真样本，其中前20个为训练样本，另外100组为测试样本，共生成720组数据，每组样本均为60维，总计43200个质量特性值点。

首先，对6种质量模式序列原始数据提取均值特征。均值特征可以有效的把正常模式、周期模式、上升趋势、下降趋势、向上阶跃、向下阶跃分为正常与周期模式、上升趋势与向上阶跃模式、下降趋势与向下阶跃模式三大类[12]，见图5a。接着，提取正常模式和周期模式的均方幅值特征和斜率特征作为PSO-SVM2的输入特征向量。由图5b可知，均方幅值特征和斜率特征可以有效的对两种模式进行区分。

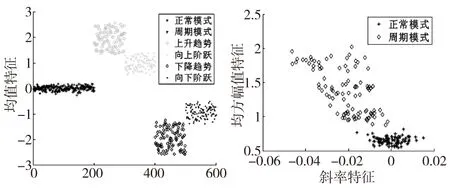
(a) (b)图5 统计特征可视化

而后，采用Db4小波函数对趋势模式和阶跃模式的原始数据进行三水平的一维离散小波分解。从图6可以得知，cA3有效去除了原始数据中的周期信号和噪声信号，保留了动态数据流的主要变化特征。因此，分别提取向上模式和向下模式的低频近似系数作为PSO-SVM4和PSO-SVM5分类器的输入特征向量。

图6 一维离散小波三层分解后的低频系数

4.2SVM训练及参数优化

实验基于MATLAB和LIBSVM工具箱，模型是支持向量分类机(SVC)。利用PSO算法确定SVM的最优参数组合。其中，PSO算法的设定参数C的范围为[0.1,100]，参数的变化范围为[0.01,1000]；粒子进化代数为200次，PSO种群数量为20，加速常数C1和C2的值设定为1.5和1.7。参数初始化完成后，利用统计特征、小波低频近似系数多特征对每个SVM进行参数优化及训练，本文模型的识别精度及参数见表1。

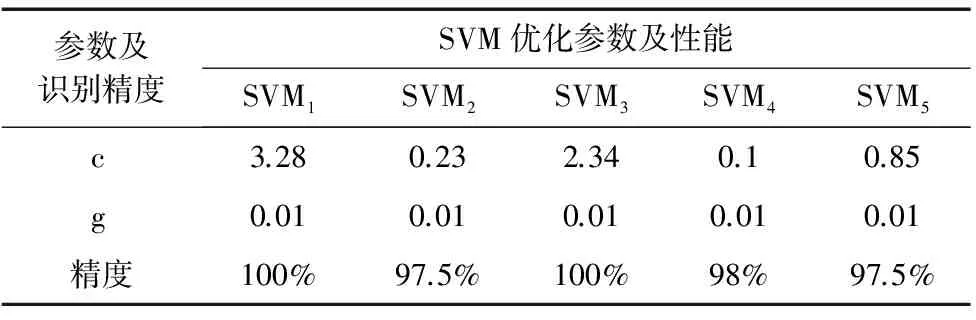
表1 SVM-RBF参数优化及识别性能

4.3 试验结果对比分析

为验证本文所提模型对质量模式识别的有效性，利用上述Monte Carlo方法产生的720组相同数据对不同方法的识别性能进行对比，其中每种模式下的训练集和测试集分别为20组和100组。首先利用粒子群算法对SVM-RBF的参数进行寻优，将所提多特征分别与原始特征、统计特征、和小波分解近似系数与统计特征混合下的PSO- MSVM进行对比，识别性能见表2。

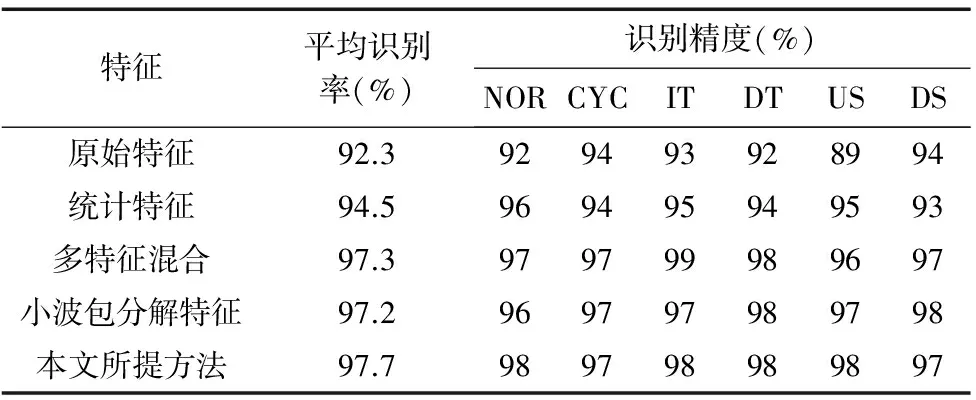
表2 基于不同特征的识别结果

由表2可知，采用不同特征提取方法，模型的识别性能也有较大差异。原始特征中包含有大量的噪声，无法取得较高的识别精度；使用单一种类统计特征对动态过程质量模式进行识别时，总体识别精度相对较低，为94.5%；多特征混合模型的总体识别精度分别为97.3%。基于统计特征特征的识别方法会造成质量模式序列的信息缺失，因此相比原始数据其识别率提升有限；基于多特征混合和小波包方法的识别模型在一定程度上弥补了单一特征的信息缺失，但其会增加特征维度，从而降低模型的识别效率。而本文所提模型能根据不同质量模式的特点提取维度低、表征能力强的特征，并与MSVM相结合，大大降低了模型的计算复杂度。仿真实验表明，基于多特征的MSVM模型对动态过程质量异常模式具有较好的监控性能。

5 结束语

本文根据各个质量模式的特点提出了一种基于多特征与MSVM的动态过程质量实时监控新方法。该方法首先采用均值特征将动态过程质量模式分为两大类，即正常与周期模式和阶跃与趋势模式，并进一步将阶跃与趋势模式分为向上模式和向下模式。通过提取均方幅值特征和斜率特征进一步区分正常模式和周期模式；通过一维离散小波的低频近似系数对向上模式和向下模式进行进一步分类。然后，使用粒子群算法实现对分类器的参数优化，并进一步训练得到支持向量机分类器。通过与单一特征、混合特征识别模型的分类性能进行对比，仿真结果表明，该方法有如下特点：(1)均值特征、斜率特征、均方幅值能够有效的降低分类器输入向量的特征维数，其中，斜率特征和均方幅值特征能够有效的对周期模式和正常模式进行区分，在提升分类器性能的同时，提高训练和识别效率。

(2)一维离散小波低频近似系数能够过滤掉周期信号和噪声信号，保留趋势信号和阶跃信号，可有效的对上述两种信号做出分类。但从图6可知，第三层低频近似系数已经破坏了原始数据中的一些关键信息，并且随着分解水平的增加，信息缺失更为明显，如何使得特征更能突出原始数据的趋势变化特性需要进一步研究。

[1] 桌德保, 徐济超. 质量诊断技术及其应用研究综述[J].系统工程学报, 2008, 23(3)：101-104.

[2] Petros X, Talayeh R. A weighted support vector machine method for control chart pattern recognition[J]. Computer&Industrial Engineering, 2014, 70：134-149.

[3] 赵方方,何桢. 基于SVM的控制图模式识别方法研究[J].组合机床与自动化加工技术, 2009(8)：1-4.

[4] Du S C, Huang D L,Jun L. Recognition of concurrent control chart patterns using wavelet transform decomposition and multiclass support vector machines[J]. Computers & Industrial Engineering, 2013, 66 (5): 683-695.

[5] A Hassan, M Shariff,AM shaharoun,et al. Improved SPC chart pattern recognition using statistical features[J]. International Journal of Production Research, 2003, 41(7): 1587-1603.

[6] 吴少雄. 基于小波概率神经网络的控制图模式识别[J]. 中国机械工程, 2006,17(s2): 135-139.

[7] Vahid R,Ata E,Reza G. Application of the PSO-SVM model for recognition of control chart patterns[J]. ISA Transaction, 2010,49:577-586.

[8] Ata E, Jalil A, Vahid R. Recognition of control chart patterns using an intelligent technique[J]. Applied Soft Computing, 2013,13(5):2970-2980.

[9] 张宇波, 蔺小楠. 改进序列向前选择法(ISFS)和极限学习机(ELM)相结合的SPC控制图模式识别方法[J]. 青岛科技大学学报(自然科学版), 2015,35(2): 322-326.

[10] 刘玉敏,周昊飞.基于MSVM的多品种小批量动态过程在线质量智能诊断[J].中国机械工程, 2015,26(17):2356-2363.

[11] 张敏,程文明.基于自适应粒子群算法和支持向量机的控制图模式识别[J].工业工程,2012,15(5):125-129.

[12] 刘玉敏,周昊飞.基于小波重构与SVM-BPNN的动态过程在线智能监控[J].系统工程理论与实践, 2016, 36(7)：1890-1897.

(编辑 李秀敏)

Dynamic Process Abnormal Monitoring Based on Multi-features with MSVM

LIU Yu-min，ZHAO Zhe-yun

(Business School, Zhengzhou University, Zhengzhou 450001, China)

In order to improve the monitoring efficiency and accuracy for abnormal patterns in dynamic process, a novel method proposed in this paper selected statistical features and wavelet approximation coefficients as input features for classifier that is constructed through multi-class SVM. Firstly, the mean characteristics extracted from data flow of dynamic process could effectively recognize the patterns including normal and cyclic patterns, increasing trend and upward shift, and decreasing trend and downward shift patterns. Then, SVM based on the features of root mean square and slope are used to develop the discrimination between normal pattern and cyclic pattern. Finally, approximation coefficients are used to recognize shift pattern and trend patterns. The simulation result show that the recognition accuracy of proposed method has a remarkable improvement of performance and computational efficiency, which is a efficient way for abnormal monitoring in dynamic process.

dynamic process; quality abnormal patterns; wavelet transform; statistics features; support vector machine

1001-2265(2017)02-0077-04

10.13462/j.cnki.mmtamt.2017.02.019

2016-09-27；

2016-11-13

国家自然科学基金资助项目(71272207,71672182)

刘玉敏(1956—)，女，河南濮阳人，郑州大学教授，博士，博士生导师，研究方向为质量控制、质量智能诊断，(E-mail)zzuyml@163.com；通讯作者：赵哲耘(1993—)，男，河南遂平人，郑州大学硕士研究生，研究方向为质量智能诊断，(E-mail)zhaozheyun@qq.com。

TH166;TG506

A