滚动导轨副的运动误差分析*
马雅丽,秦高雄,钱 峰,申会鹏
(大连理工大学 机械工程学院,辽宁 大连 116024)
滚动导轨副的运动误差分析*
马雅丽,秦高雄,钱 峰,申会鹏
(大连理工大学 机械工程学院,辽宁 大连 116024)
为研究滚动导轨副几何误差与运动误差之间的映射关系,构建出双导轨四滑块滚动导轨副的运动误差分析模型。通过运动误差分析模型的位姿误差等效方程,将运动部件位姿误差等效为四滑块中滚动体的误差变形。基于赫兹接触理论,建立运动部件的滚动体静力平衡方程,联立求解误差等效方程与静力平衡方程得出滚动导轨副的运动误差。根据运动误差分析模型,分析了导轨几何误差影响下的滚动导轨副运动误差变化规律。最后,建立滚动导轨副的有限元模型。经有限元模型与运动误差分析模型计算结果的对比,验证了文中所建模型的有效性。
滚动导轨副;导轨几何误差;运动误差分析;有限元等效
0 引言
滚动导轨副的运动精度等级取决于滚动导轨的生产等级以及导轨的几何精度。安装后导轨的几何误差是滚动导轨副产生运动误差主要影响因素之一。为了提高滚动导轨副的运动精度,常常对导轨安装面进行再修整以减小导轨的几何误差。但由于很难根据经验判断导轨几何误差与运动误差之间的映射关系,所以导轨安装面的修整过程具有一定的盲目性。因此有必要建立滚动导轨副的运动误差模型,研究导轨几何误差对运动误差副影响规律。这无疑是减小导轨几何误差以提高运动精度需要解决的关键问题之一。
针对滚动导轨副性能的研究,孙健利等[1-3]对滚动导轨的静态特性进行了试验与研究,并根据Palmgren及Harris理论,分析了几何尺寸与性能之间的关系。祝书龙等[4]推导出滚动导轨工作状态的线刚度计算公式,分析了载荷对结合部刚度特性的影响规律。Shimizu[5]基于赫兹接触理论,通过确定滚动体承受载荷与变形之间的关系,建立了滚动导轨副的静力学模型。衡豪等[6]通过设计导轨副静刚度试验装置为滚动导轨副性能的提高提供了有利条件。徐丹等[7]提出了一种新的导轨副运动精度测试与分析方法,有效提高了运动误差检测精度。Khim、Park等[8]通过构建导轨形状误差与滑块作用力之间的传递函数,建立多滑块运动平台的运动误差预测模型。Pawel Majda[9]则是通过有限元方法对机床导轨的几何误差进行等效,并建立导轨误差对机床滚动导轨副运动误差影响的分析模型。
综上,尽管滚动导轨副的运动误差分析方面的研究取得了一定的进展,但未考虑双导轨几何误差对四滑块运动部件运动误差的影响[8]。文献[9]虽然考虑了两导轨的几何误差,但有限元方法计算效率很低,并不能满足实际的应用需求。鉴于此,本文考虑双导轨几何误差对四滑块运动部件运动误差的影响。通过运动部件位姿误差等效方程与静力平衡方程构建,建立滚动导轨副的运动误差分析模型,研究在导轨几何误差影响下的运动部件运动误差变化规律,为导轨安装面的修整提供科学依据。
1 滚动导轨副的运动误差分析建模
本文以双导轨四滑块的滚动导轨副为研究对象。运动部件与四滑块固联、固定部件与双导轨固联,通过滚动体的动联接实现相对直线运动。由于导轨的几何误差因素,运动部件在导轨上某一位置的位姿会产生误差。滚动导轨副的运动误差则表现为随运动部件位置移动而连续变化的位姿误差。
运动部件位姿误差是四滑块中滚动体产生协调误差变形的根源。为此需研究滑块、导轨两滚道曲率中心的位置变化规律,寻求位姿误差参数与滚动体误差变形量间的耦合关系,提出运动部件位姿误差转化为滚动体误差变形的等效方法;通过对运动部件进行受力分析,建立运动部件内部四滑块系统中的多滚动体力学模型,求解运动部件位姿误差参数。
1.1 位姿误差几何等效方法
运动部件的位姿误差改变了滑块与导轨两滚道曲率中心之间的位置关系,因而引起两滚道之间滚动体的误差变形。为此,分析滑块、导轨滚道曲率中心的位置变化与运动部件位姿误差、导轨形位误差之间的几何关系,提出运动部件位姿误差的等效方法。
首先在固定部件上建立坐标系(OXYZ)f,在运动部件与四滑块的装配体上建立坐标系(OXYZ)m,如图1所示。
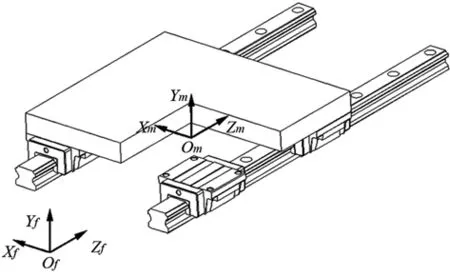
图1 滚动导轨副的坐标系
运动部件位姿误差使得实际运动部件坐标系(O′X′Y′Z′)m相对于理想运动部件坐标系(OXYZ)m产生误差变形,可以通过5个位姿误差参数ε(z)=(δx,δy,θx,θy,θz)表示(由于忽略丝杠对滚动导轨的影响,故认为在运动方向上不发生误差变形)。其中,δx(z)、δy(z)为X轴、Y轴方向的位置误差,θx(z)、θy(z)、θz(z)为绕三轴方向的角度误差,如图2所示。
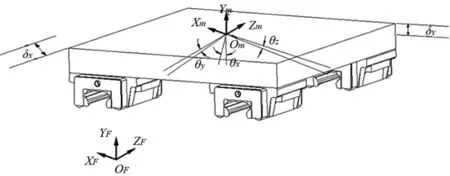
图2 运动部件位姿误差变化
Δx,ijk(z)=δx+sinθyzijk+sinθzyijk,
Δy,ijk(z)=δy+sinθxzijk+sinθzxijk
(1)
式中,xijk、yijk、zijk分别为滑块曲率中心在四滑块运动部件坐标系(OXYZ)m中三个方向的坐标值,下标i、j、k分别表示滚动导轨副中的滑块序号、滚道序号、某列滚动体序号。

图3 滑块滚道曲率中心位置变化

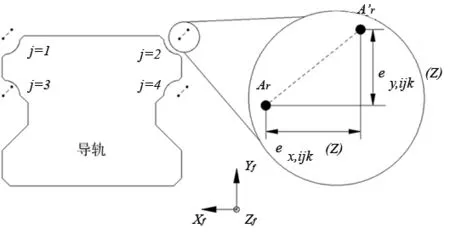
图4 导轨滚道曲率中心位置变化
导轨滚道曲率中心的误差曲线可以通过测量导轨若干截面,并以曲线拟合的方式得到,如采用傅里叶级数拟合的曲线方程为:

(2)
式中,n是谐波阶数,a0、an、λ与φn为傅里叶级数拟合系数。
滚动体的变形量与两滚道曲率中心的几何关系及滚动体的预紧力变形直接相关。理想情况下,滚动体的变形量仅为滚动体的预紧力变形。而实际情况下,导轨与滑块曲率中心的位置发生偏移,滚动体的变形量也会发现相应变化,其变形几何关系如图5所示,可以用位姿误差等效方程得出:
(3)
其中,
Vx,ijk(z)=l0cosβ+Δx,ijk(z)+ex,ijk(z)
Vy,ijk(z)=l0sinβ+Δy,ijk(z)+ey,ijk(z)
l0=2R-d
式中,l0为两滚道理想曲率中心Ab与Ar之间的距离,χd为滚动体的预紧力变形,d为滚动体的直径,β为滚动体的理想接触角,R为滚动导轨中导轨与滑块滚道曲率半径(假设两滚道曲率半径相同)。

图5 滚动体误差等效几何关系
1.2 位姿误差参数的求解
基于赫兹接触理论,构建出滚动体的误差变形量与弹性回复力之间的对应关系。滚动体误差变形以弹性回复力形式作用于滑块及运动部件。四滑块运动部件为静力平衡系统,建立运动部件的静力平衡方程,求解五个误差变形参数。
运动部件位姿误差引起了四个滑块中所有滚动体的误差变形。取某一滚动体作为研究对象,滚动体的误差变形与弹性回复力大小之间的关系可用赫兹接触方程进行表述[10]:
(4)
式中,η为与滚动体直径、滚道曲率半径相关的接触系数。


图6 滚动体的弹性回复力
四个滑块中所有滚动体都会产生弹性回复力作用于运动部件,建立运动部件的力与力矩的平衡方程。
(5)
运动部件位姿误差的求解过程由于涉及滚动体变形较多,且赫兹接触变形为非线性,无显性表达式,因此采用数值方法求解,求解步骤如下:
(1)设定运动部件的位置z,假设运动部件的位姿误差参数εi(z)=εi0(z)(如εi0(z)=0),由导轨滚道曲率中心误差拟合曲线(2)与误差等效方程(3),得到运动部件四个滑块中所有滚动体的误差变形量Δdijk。
(2)基于赫兹接触方程(4)得出所有滚动体的弹性回复力。
(3)由静力平衡方程(5)计算当前位置下的载荷不平衡量,得到新的位姿误差参数εi,并返回第(1)步,当载荷不平衡了满足精度要求时停止迭代,最后一步计算结果即为运动部件位置为z时的求解结果。
(4)改变运动部件的位置z,求得运动部件在导轨上各个位置的位姿误差,得到运动部件的多自由度运动误差(沿X向、Y向直线度误差δxz、δxz及俯仰角误差θxz、偏转角误差θyz、回转角误差θyz)。
2 滚动导轨副的运动误差特性分析
基于滚动导轨副的运动误差分析模型,分析导轨几何误差作用对滚动导轨副运动误差的影响规律。
2.1 运动误差分析对象
以图7所示的双导轨四滑块的滚动导轨副为例,建立滚动导轨副的运动误差分析模型。两导轨的跨距Lr=250mm,滑块之间的间距Lb=300mm,滚动导轨副的行程为1200mm。滚动导轨型号为选用THK公司的HSR-45,滚动体直径d=8mm,滚动体的理想接触角β=45°。

图7 滚动导轨副结构
假定左右两个导轨竖直方向的几何误差通过式(2)第一阶傅里叶级数进行拟合,且a0=0,即:
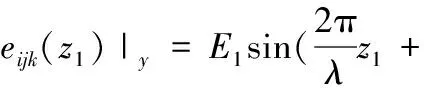

(6)
波长、幅值与相位是滚动导轨副中两导轨几何误差的主要参数。根据滚动导轨副的运动误差分析模型,本节主要分析两导轨上这三个主要参数对运动误差的影响规律。
2.2 几何误差中相位对运动误差的影响规律
滚动导轨副中两导轨几何误差幅值与波长相同,当相位差分别为0、90°、180°、270°时,通过数值仿真得滚动导轨副的运动误差如图8所示。

(a)直线度误差

(b)俯仰角误差

(c)回转角误差图8 不同相位角的运动误差结果
直线度误差、俯仰角误差随相位差变化的规律相同,与回转角误差相反。在相位差为0时,前两者达到最大值,后者为零;在相位差为180°时,前两者为零,后者达到最大值。运动误差随导轨几何误差相位差变化的规律可以通过公式(3)解释。当相位差为0时,导轨上两滑块中滚动体的变形随几何误差变化,但左右两导轨相对应的滑块中滚动体的变形分别相同,因此四个滑块的弹性回复力仅使运动部件受到沿Y向的力与绕X轴的力矩,绕Z轴的力矩为零。而当相位差为180°,左右导轨相对应的滑块中滚动体的变形分别相反,因此运动部件沿Y向的力与绕X轴的力矩为零,绕Z轴的力矩达到最大。
2.3 几何误差中波长对运动误差的影响规律
滚动导轨副中两导轨几何误差的相位与幅值相同,定义几何误差波长比为滑块间距与波长的比值Lr/λ。当几何误差波长比Lr/λ在0.1~10之间变化时,通过数值仿真得滚动导轨副的运动误差如图9所示。

(a)直线度误差

(b)俯仰角误差图9 不同波长的运动误差结果
从图9计算结果可以看出,几何误差的波长是影响滚动导轨副运动误差的重要因素。当0.1≤L/λ≤1时,直线度误差先减小后增大,俯仰角误差先增大后减小。当1 2.4 几何误差中幅值对运动误差的影响规律 滚动导轨副中两导轨几何误差的波长与相位相同,当导轨几何误差幅值分别为2μm、5μm、10μm,通过数值仿真得到滚动导轨副的运动误差如图10所示。 (a)直线度误差 (b)俯仰角误差图10 不同幅值的运动误差结果 不同幅值的运动误差结果看出,在波长与相位角确定的情况下,随导轨几何误差幅值的增大,直线度误差与俯仰角误差的幅值也作了相应的变化。在此定义几何误差与运动误差的映射系数: (7) Eδy、Eεx分别为直线度误差与俯仰角误差的幅值。在本例波长λ=400mm,相位差为零的情况下,K1=1.85μm/μm、K2=2.84μrad/μm。 提出导轨几何误差的有限元等效方法。根据等效方法,建立考虑导轨几何误差影响的运动误差分析的有限元模型。将有限元计算结果与运动误差模型计算结果进行对比,验证本文建立的滚动导轨副运动误差分析模型的有效性。 3.1 导轨几何误差的有限元等效模型 建立滚动导轨的有限元模型。基于节点偏移方法,将导轨几何误差等效弹簧单元的变形,构建导轨几何误差的等效模型。 滚动导轨的实体模型经有限元网格划分为实体单元。为了模拟滚动体与滚道间的非线性接触特性,利用多个非线性弹簧单元等效滑块中的滚动体。弹簧单元的两节点分别为导轨、滑块滚道的曲率中心,其刚度特性可由滚道间滚动体接触变形的赫兹接触分析得到[9];导轨、滑块滚道的曲率中心分别与滚动体与滚道接触区域建立刚性耦合区域。滚动导轨的有限元模型如图11所示。 图11 滚动导轨有限元模型 导轨的几何误差使得导轨滚道曲率中心产生偏差,进而影响滚动体的变形量。因此在有限元等效模型,通过节点偏移方法,偏移导轨滚道曲率中心节点,使得弹簧单元的变形量产生相应的变化。 Δd=l-l0 (8) 图12 弹簧单元的变动几何关系 3.2 滚动导轨副的运动误差分析 建立滚动导轨副的有限元模型。通过有限元方法,研究导轨几何误差影响下的运动部件位姿误差。导轨几何误差相同时,对比有限元计算运动误差与运动误差分析模型计算结果。 有限元的运动误差分析模型采用的对象为2.1节中的滚动导轨副,如图13所示。组件中导轨与固定部件固联,因此导轨底面进行全约束;丝杠等效为弹簧单元,约束运动部件的运动自由度。 图13 滚动导轨副的有限元模型 假定导轨在竖直方向上滚道曲率中心存在正弦型几何误差,波长为λ=400mm,幅值E1=10μm,E2=0。根据3.1节的导轨几何误差等效,导轨的几何误差等效为有限元模型中弹簧单元的误差变形。通过有限元求解得出在导轨几何误差影响下运动部件的运动误差。 根据本文建立的运动误差分析模型,考虑上述正弦型几何误差的影响,得出对应的运动误差结果。分别从有限元分析模型与运动误差模型的计算结果中提取运动部件上关键点P1、P2的运动误差参数进行对比,如图14所示。 (a)关键点P1的直线度误差 (b)关键点P2的直线度误差图14 运动误差计算结果对比 从图14的结果对比看出,两个模型沿Y轴的运动位置误差计算结果波动基本一致。两个模型中关键点P1的位置误差波动幅值分别为6.8μm与8.5μm,关键点P2的位置误差波动幅值分别为7.2μm与8.8μm,由此可见两种模型计算结果偏差较小,因此可以验证滚动导轨副运动误差分析模型的有效性。 针对双导轨四滑块的滚动导轨副,建立了新的运动误差分析模型,构建出出导轨几何误差与运动误差之间的映射关系,经分析与计算,得出以下结论: (1)滚动导轨副中两导轨几何误差的相位、波长与幅值都会改变运动部件四个滑块中滚动体的变形,从而对运动部件运动误差产生影响。随导轨几何误差 的相位差变化,直线度、俯仰角误差与回转角误差的变化规律相反;当L/λ为整数时,直线度误差与俯仰角误差分别出现极大值与极小值,且当L/λ>1时,运动误差量级急剧减小;滚动导轨副的直线度误差与俯仰角误差幅值随导轨几何误差幅值变化呈线性变化规律。 (2)经过滚动导轨副运动误差分析模型与有限元模型的对比分析,两关键点的直线度误差均在0.4μm以内,从而验证了滚动导轨副运动误差分析模型的有效性与准确性。 [1] 孙健利. 直线滚动导轨机构承受垂直载荷时的刚度计算[J]. 华中理工大学学报,1988,16(5):35-40. [2] 孙健利. 精密直线滚动导轨的预加载荷及刚度计算[J]. 华中理工大学学报,1988,16(6):125-130. [3] 孙健利,赵虎,陈锐. 滚动直线导轨副滚道几何尺寸与性能的关系[J]. 制造技术与机床,2001(10): 18-20. [4] 蒋书运,祝书龙. 带滚珠丝杠副的直线导轨结合部动态刚度特性[J]. 机械工程学报,2010,46(1): 92-99. [5]ShimizuS.Stiffnessanalysisoflinearmotionrollingguide.JournaloftheKoreanSocietyforPrecisionEngineering. 1998, 64(11): 1573-1579. [6] 衡豪,王禹林,冯虎田. 滚动直线导轨副静刚度试验装置设计及试验方案研究[J]. 组合机床与自动化加工技术, 2014(2):106-109. [7] 徐丹,梁医,欧屹,等. 滚动直线导轨副运动精度测试与分析方法研究[J]. 组合机床与自动化加工技术,2015(1): 126-129. [8]KhimG,ParkCH,ShamotoE,etal.Predictionandcompensationofmotionaccuracyinalinearmotionbearingtable[J].PrecisionEngineering,2011, 35: 393-399. [9]MajdaP.Modelingofgeometricerrorsoflinearguidewayandtheirinfluenceonjointkinematicerrorinmachinetools[J].PrecisionEngineering, 2012, 36: 369-378. [10] 孙伟,孔祥希,汪博,等. 直线滚动导轨的Hertz接触建模及接触刚度的理论求解[J]. 工程力学,2013,30(7): 230-234. (编辑 李秀敏) Motion Error Analysis of a Linear Motion Bearing Table MA Ya-li, QIN Gao-xiong, QIAN Feng, SHEN Hui-peng (School of Mechanical Engineering, Dalian University of Technology, Dalian Liaoning 116024, China) An analysis model for motion error of a linear motion bearing table with two rails and four bearing blocks is proposed to research on the relationship between geometrical errors and motion errors. Potion and pose errors of the moving table are mapped into the elastic deformation of rolling elements in the four blocks by using the error equivalent equation of this model. According to the theory of Hertz contact, rolling elements’ static force equilibrium equation of the table is established. Motion errors are obtained with combining and solving the error equivalent equation and static force equilibrium equation. Based on this model, the influence of geometrical errors on the motion errors is analyzed. At last, a finite element model of a linear motion bearing table is built. After comparing the results of the analysis model and the finite element model, the analysis model’s validity in this article is proved. linear motion bearing table; rail geometric error; motion error analysis; equivalent method of finite element 1001-2265(2017)02-0005-06 10.13462/j.cnki.mmtamt.2017.02.002 2016-04-20; 2016-05-10 国家科技重大专项(2015ZX04014-021) 马雅丽(1963—),女,满族,辽宁鞍山人,大连理工大学副教授,硕士生导师,博士,研究方向为机械系统设计及创新设计理论方法研究,(E-mail)myl@dlut.edu.cn。 TH166;TG506 A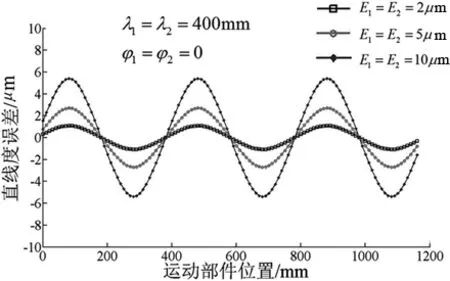

3 滚动导轨副的有限元模型及运动误差分析






4 结论

