新型龙门式混联机床主体机构的动态特性分析*

马春生，李俊帅，李瑞琴，胡 洋

(中北大学 机械与动力工程学院，太原 030051 )

新型龙门式混联机床主体机构的动态特性分析*

马春生，李俊帅，李瑞琴，胡 洋

(中北大学 机械与动力工程学院，太原 030051 )

以一种新型龙门式混联机床主体机构为研究对象，对该混联机床主体机构的动态特性进行研究。首先运用SolidWorks对其主体机构建立三维实体模型，然后导入到有限元分析软件ANSYS Workbench进行模态分析，得到主体机构的一到六阶固有频率和振型，找出机构运动过程中易发生共振的位置，并且得出混联机床主体机构的各阶固有频率均大于机床的工作频率，验证了机床主体机构设计的合理性。在模态分析的基础上，对该混联机床进行谐响应分析，得出动平台在X，Y，Z轴方向的位移响应曲线，从而验证该混联机床的抗振性能，得出机构应避免的敏感频率，这为该混联机床的进一步动态设计与优化奠定了基础。

混联机床；并联机构；有限元；模态分析；谐响应分析

0 引言

20世纪90年代末提出的混联机床同时具有串联和并联机床的优点，可以避免因单纯串、并联所引发的问题，在现代制造业中更具有实用性，是今后机床研究的一个重要发展方向，也是创新发展各种复杂先进装备所需的新机型来源之一[1]。混联机床的主体机构作为机床最重要的组成部件，不仅是机床工作的关键部件，同时还承受着静载荷以及在加工时产生的切削负载的作用。主体机构动态特性的好坏直接影响着整台机床的工作性能，最终影响到加工工件的几何精度及表面质量，因此有必要对主体机构进行动态特性分析[2]。

张广鹏[3]等人基于边界元法研究混联数控机床整机结构动态特性的解析和建模方法。孟祥志[4]等人利用ADAMS软件对3-TPS型混联机床进行振动测试分析和加工仿真分析。李兴山[5]等人提出了一种新的三自由度混联机床构型，并利用误差独立作用原理，建立了误差分析数学模型。张广鹏[6]等人还基于模糊数学的原理,提出一种机床整机动态特性的评价方法。本文以一种新型龙门式混联机床主体机构为研究对象，着重考虑主体机构的动态特性，运用有限元法对主体机构进行模态及谐响应仿真分析，为该混联机床主体机构的设计提供理论参考依据。

1 主体机构的有限元模型

2-RPU&2-UPS+P 混联机床的几何结构相对有些复杂，如果在ANSYS Workbench中直接建模存在困难，因此运用SolidWorks进行三维实体建模[7]。由于并联机构在建模的过程中本身存在一些复杂性，因此在导入ANSYS Workbench 之前，对模型应进行合理的简化，具体过程为：①利用SolidWorks建模时，要保证尺寸准确，避免发生干涉，这样可以避免一些错误的发生。②对零件中存在的小孔、倒角等微小的特征进行删除和简化，这样有利于下一步网格的划分。③对动平台、导向杆等零件做简化处理。④对该机床零件间的配合关系进行简化，消除运动副间存在的间隙。对模型进行简化后，得到最终的模型如图1所示。

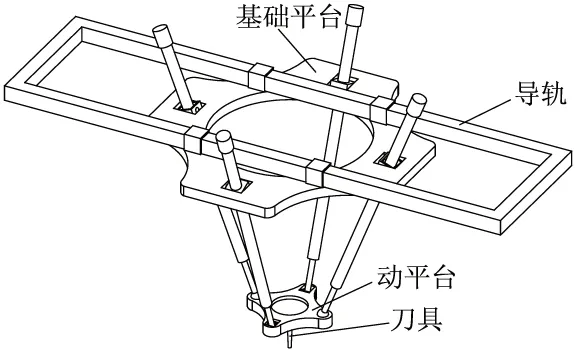
图1 简化模型图

将建立的三维模型导入到Workbench中建立相应的有限元模型，具体过程如下：

(1)定义单元和材料属性：由于模型复杂的空间几何结构，所以设置单元类型为四面体。材料采用结构钢，弹性模量为2×105MPa、泊松比为0.3、密度为7.85×10-6kg·mm-3。

(2)网格划分：采用均匀的网格划分形式[8]。

2 模态分析

2.1 模态分析基本原理

由机械振动理论的知识可知，对于一个确定的结构，其运动微分方程为：

(1)

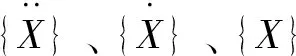
由于阻尼对固有频率和振型几乎没有影响，所以忽略阻尼项，得到新的运动微分方程：

(2)

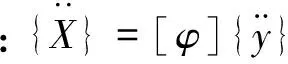
在无阻尼自由振动时，结构中各节点的振幅不全为0，因此可得结构的自振频率方程为：

(3)

对公式(3)进行求解，ω可得到n个解，即可以得到结构自由振动时的固有频率：

(4)

2.2 模态分析结果及结论

由于低阶模态对结构的性能影响较大，高阶模态的影响很小，所以这里只选取一到6阶进行研究。在模态分析的过程中，Fixed Support约束是唯一有效的载荷，其他的载荷将被忽略。根据机构实际的情况选择将导轨进行固定，然后做无阻尼自由振动。表1为模态频率，单位为Hz，图2为1～6阶振型图。

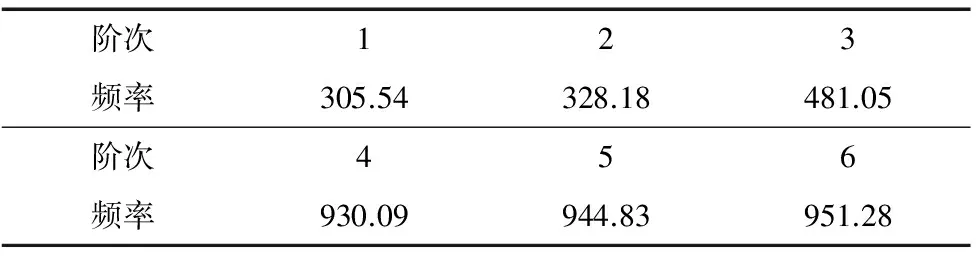
表1 该混联机床前6阶固有频率表

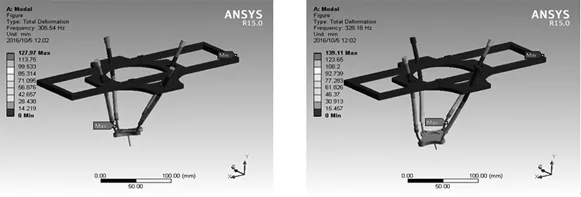
(a)第1阶振型 (b)第2阶振型

(c)第3阶振型 (d)第4阶振型

(e)第5阶振型 (f)第6阶振型图2 该混联机床前六阶振型图

1阶振型的固有频率为305.54Hz，振型主要表现为各个分支在YZ平面上的弯曲变形，主要发生在动平台及与其相连的各个分支处，其中各个分支的移动副联接处振幅达到最大，其振型如图2a所示。

2阶振型的固有频率为328.18Hz，振型主要为各个分支在XY平面的弯曲变形，主要发生在动平台及与其相连的分支处，在各个分支的移动副联接处振幅达到最大，其振型如图2b所示。

3阶振型的固有频率为481.05Hz，振型主要表现为动平台在XZ平面上的扭转，在动平台与各个分支的连接处振幅最大，其振型如图2c所示。

4阶振型的固有频率为930.09Hz，振型主要为两条UPS 分支在YZ平面内的1阶同向弯曲变形，并且对称，在UPS分支的末端处振幅最大，其振型如图2d所示。

5阶振型的固有频率为944.83Hz，振型主要表现为两条UPS分支在XY平面内的1阶反向弯曲变形，在该分支的末端处振幅最大，其振型如图2e所示。

6阶振型的固有频率为951.28Hz，振型主要表现为两条UPS 分支在YZ平面上的1阶反向弯曲变形，在该分支的末端处振幅最大，其振型如图2f所示。

通过上述机构1～6阶的比较可知，第1、2、3阶的固有频率远小于4、5、6阶，说明第1、2、3阶的运动刚度远小于4、5、6阶。通过上述频率与振型可知，动平台和各个支链与相邻部件连接处的刚度比较弱，是机构的薄弱环节，可以换用刚度较好的材料来提高其抗振特性。而且机床主体机构的前6阶固有频率都在300Hz以上，且均大于机床电机的工作频率133.3Hz(机床电机的转速为8000r/min)，由此可知，该机床主体机构的设计有效地避开了共振区域，其固有频率离工作共振频率较远，初步认定该机床主体机构的设计是合理的，不会发生共振破坏。

3 主体机构的谐响应分析

模态分析只能表示出机构本身的固有频率和振型， 而谐响应分析可以表示出机构在受到不同频率简谐载荷下的变形，对于克服共振现象和疲劳响应具有重要意义。利用Workbench有限元软件，运用完全法对该混联机床进行谐响应分析。求解条件如下：沿Y轴方向在动平台上施加应力幅值，大小为100N；结构阻尼比设为0.02；根据模态分析得出的结果，简谐力的频率范围设为300～1000Hz；将载荷子步数设置为50，则在该频率段内对应有50个谐响应解。该机床动平台沿X、Y、Z三个方向的位移响应曲线，如图3～图5所示。

图3 动平台沿X轴方向的位移响应曲线

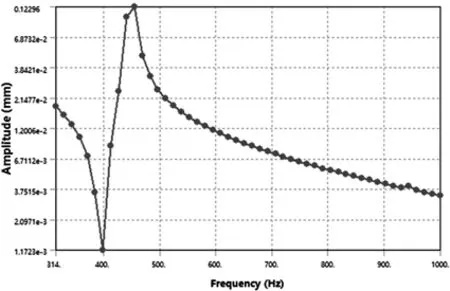
图4 动平台沿Y轴方向的位移响应曲线

图5 动平台沿Z轴方向的位移响应曲线

通过观察图3～图5的位移响应曲线，可以发现：

(1)动平台在1～6阶固有频率处均产生较大的响应，这与前面模态分析的结果保持一致。

(2)动平台沿X轴方向的位移幅值在第2阶固有频率附近约330Hz 处达到峰值，Y轴方向的位移幅值在第3阶固有频率约460Hz 处达到峰值，Z轴方向的位移幅值在第3阶固有频率约480Hz 处达到峰值。由此可得出在2阶与3阶固有频率附近，动平台沿各个方向产生的响应最大，而在其它阶固有频率处产生的响应相对较小，说明2阶和3阶固有频率对该混联机床的动态性能影响最大，机床对328.18Hz和481.05Hz频率最为敏感， 因此为了保证机床的运行精度应避开上述频率。

(3)动平台位移响应曲线沿X和Z轴方向走势基本保持一致，表明这两个方向的移动刚度相似，这主要是由于该混联机床结构上的对称性造成的。对于该机床的动平台而言，Y轴方向的位移量是最大的，比X轴方向的动态位移量高出约一个数量级，Z轴方向的位移量最小。

(4)从上述响应曲线可以看出，如果该混联机床不发生共振，工作时该机床在X和Y轴方向的响应通常为0.01mm级，而Z轴方向的响应相对较小可忽略不计。

4 结论

(1)通过模态分析，获得该混联机床1～6阶的固有频率和振型，找出了该机床运动过程中易引起共振的位置。而且可以得出该机床主体机构的前 6阶固有频率均大于机床工作频率，不会发生共振破坏，初步验证了机床主体机构设计的合理性。

(2)在模态分析的基础上对该混联机床进行了谐响应分析，得出动平台在简谐载荷作用下的振动位移特性，找出该混联机床应该避开的工作频率， 为该混联机床的进一步优化设计和控制提供了重要的理论依据。

[1] 沈惠平，赵海彬，邓嘉鸣，等. 基于自由度分配和方位特征集的混联机器人机型设计方法及应用[J]. 机械工程学报，2011，47(23)：56-64.

[2] 杨玉萍,张森,季彬彬,等. 立式加工中心床身结构动态特性有限元分析[J]. 机械设计与制造,2014(1):174-176.

[3] 张广鹏,方英武,张灿果,等. 基于边界元法的混联数控机床整机结构动态特性解析[J]. 机械强度,2005(2):140-145.

[4] 孟祥志,赵柏庆. 基于ADAMS的3-TPS混联机床动态特性分析[J]. 机床与液压,2014,42(9):6-9.

[5] 李兴山,蔡光起. 三自由度混联机床的机构误差分析与仿真[J]. 组合机床与自动化加工技术,2011(3):19-22.

[6] 张广鹏,黄玉美,赵宏林,等. 一种机床动态特性的模糊评价方法[J]. 制造技术与机床,2001(1):20-22.

[7] 韩春胜,孙皆宜. 6-PUS并联机床的动态特性分析[J]. 机械设计与制造,2013(6):161-164.

[8] 方利卡. GQ1070龙门加工中心结构动态特性分析[D].杭州:浙江工业大学,2012.

[9] 付铁,丁洪生,李金泉,等. BKX-Ⅰ型并联机床的谐响应分析[J]. 现代制造工程,2005(9):32-33.

[10] 彭俊泉,任衍坤,刘晶晶,等. 基于3UPS-UP并联机构的磁流变液抛光装置有限元分析[J].组合机床与自动化加工技术,2015(7):37-40.

[11] 左晓明. 基于SolidWorks的变速箱变速机构模态分析[J].机械传动,2011(5):49-51.

[12] 邓嘉鸣,沈惠平,王玮,等. 用于光电产品检测的混联6-dof平台的刚度及模态分析与仿真[J]. 机械设计与研究,2016(8):15-19.

(编辑 李秀敏)

Dynamic Characteristics Analysis of the Main Body of the New Longmen Type Hybrid Machine Tool

MA Chun-sheng, LI Jun-shuai,LI Rui-qin,HU Yang

(School of Mechanical and Power Engineering, North University of China, Taiyuan 030051,China)

Taking the main body of a new type of Longmen hybrid machine tool as the research object，its dynamic characteristics were studied. Firstly the 3D model of the main mechanism was established by SolidWorks software.Then the 3D model was imported into the finite element analysis software ANSYS Workbench to finish modal analysis, one to six order natural frequency and vibration mode of the main body was got, and the resonance in the process of movement was found easily, and it is concluded that the inherent frequency of the main body of the hybrid machine tool was larger than the working frequency of the machine tool, which verified the rationality of the design of the main body of the machine tool. On the basis of modal analysis, the displacement response curve of platform alongX,Y,Zdirection was dispatched by harmonic response analysis, and the anti vibration performance of the machine was proved, and the sensitive frequency was got that the mechanism should avoid. It laid the foundation for further dynamic design and optimization of the hybrid machine tool.

hybrid machine tool;parallel mechanism;finite element;modal analysis;harmonic response analysis

1001-2265(2017)02-0011-03

10.13462/j.cnki.mmtamt.2017.02.003

2016-10-10；

2016-10-31

国家自然科学基金资助项目(51275486)

马春生(1974—)，男，山西大同人，中北大学副教授，博士，研究方向为机构理论与机器人技术，(E-mail)470351109@qq.com。

TH112;TG659

A