《函数的奇偶性》教学案例分析

杨宏亮

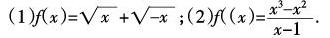
数学教学不仅是知识的教学，还应该体现数学的教育价值，提高学生对数学的认识与数学素养。而作为青年教师，在平时的教学中更应该努力熟悉教材、把握教材，达到最好的教学效果。

这是我讲过的一节汇报课，对这节课我有些思考与感悟，写出来与各位同仁作一交流。

一、案例：《函数的奇偶性》

师：在现实生活中，许多事物都给我们以对称的感觉，例如：人体的轮廓、天安门城楼、射箭用的弓等等，它们都关于某条轴对称，又如太极八卦图，又给我们中心对称的美感。而这种对称美在我们数学中又有大量的反映，请同学们拿出练习本作出函数①y=x2；②y=x；③y=x；④y=的图象，并观察、分析函数①y=x2；②y=x的图象有怎样的共同特征？

生：在教师作图的同时，很快作出这四个函数的图象，能观察出①②两个函数的图象都关于y轴对称。

师：我们把图象关于y轴对称的函数称为偶函数；图象关于原点对称的函数称为奇函数。

师直接给出奇函数、偶函数的定义。

师与学生一起分析判断函数奇偶性的条件：

1.偶函数：（1）函数的定义域是否关于原点对称；

（2）f（-x）=f（x）.

2.奇函数：（1）函数的定义域是否关于原点对称；

（2）f（-x）=-f（x）.

师：是否存在一些函数既是奇函数又是偶函数呢？

例：判断下列函数的奇偶性：

（1）f（x）=+；（2）f（（x）=.

课堂练习：课本练习2

师分析：若函数为奇函数，且定义域中有0元素，则一定有

f（0）=0。

课堂小结：教师小结奇偶性的定义和判断函数奇偶性的方法。

二、课后感想

本节课想借助实际生活中的对称关系，激发学生的学习兴趣，为使学生更好地理解奇偶性是体现“对称性”的一个重要性质打下基础，同时利用四个特殊函数①y=x2；②y=x；③y=x；④y=的图象，引导学生观察、归纳奇偶函数的图象特征，给出函数奇偶性的定义，重点学会判断函数的奇偶性，达到数形结合的效果。

三、部分學生的课堂感受

课后，我与部分学生交流本节课的感受，学生都表示通过本节课的学习学会了如何判断函数的奇偶性，但是对函数奇偶性的定义还是不太理解，有些基本概念也掌握得不是很好。

四、案例评析

1.在教材内容的理解上，首先应该看到，探究数学结构的对称性和规则性是数学活动的核心。本节课教师不论采取什么样的教学方法，都要抓住“数”与“形”的结合。所以，建议教师在引课中借助生活中的对称实例或多媒体软件，使学生直观感受这些对称美，激发学生的学习兴趣，并通过函数图象提供的半具体、半抽象的对称性，探究对称美，进而提炼出抽象的对称性——函数的奇偶性。

2.教学目标的定位。从课堂实施过程和最后阶段的反馈来看，本节课中我对教学目标的把握不够到位，淡化了对奇偶函数定义的探究、抽象，课堂落实不够好，同时也没有达到对重点的突出和难点的突破。教师更应站在学生的角度思考，精心设计教学过程，真正关注“知识与技能、过程与方法、情感态度与价值观”三维目标的有机统一。

3.在具体对称性图案与抽象表达式f（-x）=f（x）或f（-x）=-f（x）之间存在巨大的视觉差异。作为教师，就是要通过自己的课堂教学设计帮助学生克服这种视觉差异与思维上的障碍。而本节课中，教师直接给出函数奇偶性的定义，表面上看起来避免了学生思维上会出现的障碍，但实质上是对教材教学目标的把握不到位，更主要的是从某种程度上制约了学生数学思维的发展。

4.本节课的重点是理解函数奇偶性的概念，难点是抽象概括出奇函数、偶函数的定义。因此，教师在教学过程中，对于函数奇偶性的定义应完整地进行板书，且要对抽象的定义进行再分析，从数与形两个方面让学生再次体会。

5.在例题的设置上，应达到从正反两个方面来理解函数奇偶性的目的，而且从难度上应该有层次性。所以例题可以设置如下：

例：判断下列函数的奇偶性：

这样设计不但可以帮助学生更好地理解判断函数奇偶性的方法，注意到两个条件缺一不可，还可以让学生了解到根据函数的奇偶性可以将函数分为奇函数、偶函数、非奇非偶函数、既奇又偶函数这四类。

6.对学生的学习而言，重要的是在数学活动过程中，掌握数学基础知识与基本技能。从课后与学生的交流来看，本节课学生活动的设计不够，学生更多的是在看教师的展示，几乎没有他们自己的活动，更谈不上在数学学习过程中体会数学带给自己的乐趣，这样的课堂又怎么能培养学生的数学思维与数学能力呢？

而基于学生活动的教学设计应该是这样的教学过程：学生通过数学活动，发现了什么问题？新的问题与自己已有的知识结论之间有什么样的联系？是什么因素把它们联结起来的？是什么方法导致了你的发现？更进一步的学生活动境界，应是促使学生在数学活动中，自觉地学会反思。正如费赖登塔尔所说：“反思是数学思维活动的核心和动力”，“以反思为核心，才能让学生真正深入到数学化过程之中，也才能抓住数学思维的内在实质”。

编辑 张珍珍