大跨度连续梁桥与梁拱组合桥梁轨相互作用比较

戴公连，刘瑶, 2，刘文硕



大跨度连续梁桥与梁拱组合桥梁轨相互作用比较

戴公连1，刘瑶1, 2，刘文硕1

(1. 中南大学土木工程学院，湖南长沙，410083；2. 湖南大学设计研究院有限公司，湖南长沙，410082)

为了比较大跨度铁路连续梁桥与梁拱组合桥梁轨相互作用特点，以(82.9+172.0+82.9) m连续梁桥与梁拱组合桥为例，分别建立考虑钢轨−主梁−桥墩−基础、钢轨−拱肋−吊杆−主梁−桥墩−基础这2种桥梁梁轨系统一体化有限元模型，系统对比温度、活载、制动力、混凝土收缩徐变等作用下连续梁桥与梁拱组合桥上无缝线路纵向力的分布规律，并对线路纵向阻力、钢轨伸缩调节器设置等参数的影响进行探讨。研究结果表明：采用德国规范与中国无缝线路规范中的纵向阻力模型，连续梁桥钢轨伸缩力最大值与梁拱组合桥的钢轨伸缩力最大值相比分别大2.3%和2.0%；连续梁桥有载侧和无载侧钢轨最不利挠曲应力与梁拱组合桥的无载侧钢轨最不利挠曲应力相比均大67.8%；温度与断轨位置对断轨力影响显著；2类桥梁钢轨应力在同向列车制动与桥梁收缩徐变作用下变化规律与大小基本一致；对下部结构，连续梁桥对梁体升温敏感程度比连续梁拱桥的大，在挠曲工况下，两者墩顶水平力最大差为176.1 kN。

铁路桥梁；连续梁桥；连续梁−拱组合桥；梁轨相互作用；无缝线路纵向力

随着铁路建设的发展，桥上无缝线路所占比例逐渐增大。根据跨径需要，在某些条件下，简支梁桥不能满足要求，而大跨度连续梁桥与连续梁拱组合桥具有跨度大、刚度大、行车平稳、承载能力大、养护简单等优点，所以，在近代桥梁建筑中已得到越来越广泛应用。目前，国内外学者对梁轨相互作用进行了广泛研究[1−5]，如：RUGE等[2]推导了考虑加载历史的钢轨纵向力计算公式；陈嵘等[3]研究了连续梁桥上无砟轨道纵向变形的控制指标；蔡小培等[4]分析了桥上纵连板式无砟轨道的受力和变形影响规律等。相关规范也对梁轨系统计算方法进行了明确规定[6−7]，但其研究对象多为梁桥。在温度、列车、制动等荷载作用下，梁拱组合桥与连续梁桥上无缝线路的纵向相互作用规律差别还不明确。为此，本文作者采用非线性杆单元模拟线路阻力，建立同等跨度的连续梁桥与连续梁拱组合桥上无缝线路有限元模型，对比分析竖向活载、制动力、伸缩力作用下连续梁桥与连续梁拱桥无缝线路纵向力传递规律，同时考虑断缝位置、收缩徐变与基础不均匀沉降等因素对钢轨纵向力的影响，以便为同类桥梁设计提供参考。

1 工程概况

兰渝线(兰州—重庆)广元段由于跨越嘉陵江，要求跨径为(82.9+172.0+82.9) m，现提供连续梁桥与梁拱组合桥2种设计方案。其中，连续梁拱桥梁体为单箱单室、变高度、变截面箱梁，全长337.8 m，见图1(a)。箱梁顶板宽13 m，中支点处顶板局部加宽至15 m，箱底宽9.8 m。中跨中部20 m梁段和边跨端部6.9 m梁段为梁高4.5 m等高段，中墩处梁高为10 m。拱肋采用二次抛物线方程，矢高为34.4 m，矢跨比为1:5。下部基础由15根桩基组成。另外，考虑同等跨度、相同截面形式等条件下的连续梁桥方案，桥型布置见图1(b)。

(a) 连续梁拱组合桥；(b) 连续梁桥

1.1 有限元模型

对于连续梁拱组合桥，为了正确模拟吊杆与轨道的空间位置，建模时采用鱼骨刺模型[8]。钢轨与拱桥主梁、拱肋均采用梁单元模拟，在主梁与轨道之间建立刚臂用来确保轨道的空间线形，纵向阻力由非线性杆单元模拟。吊杆采用杆单元模拟，滑动支座采用顺桥向放松约束的方法，拱脚与主梁采用刚性连接的方式，并且桥梁左、右两端路基上各铺100 m钢轨。另外，连续梁桥梁轨相互作用模拟方法与连续梁拱桥的一致，仅在桥梁构造上有所差别。

1.2 计算参数选取

桥上铺设有砟轨道，钢轨重度为60 kN/m。目前，各国规范关于线路阻力的规定相差较大，本文采用我国无缝线路规范[6]与德国规范[7]中线路纵向阻力与梁轨相对位移的关系，如图2所示。

1—竖向无缝(德国规范)，；2—竖向有载(无缝线路规范)，；3—竖向有载(无缝线路规范，德国规范)，。

列车活载加载长度200余m[9]，制动力率取为0.164[10]。基础不均匀沉降作用按边墩沉降10 mm、中墩沉降20 mm考虑。

在计算桥梁收缩徐变对钢轨纵向力的影响时[11]，采用文献[12]提供的徐变曲线，其徐变系数可表示为

(,)=(∞,)·c(,)

式中：(∞,)为徐变终值；c(,)为加载后徐变发展系数；为加载龄期；为计算龄期。

2 梁轨系统相互作用分析

2.1 温度荷载作用分析

梁体升温与降温对钢轨作用效果相反，故本文分别根据铁路无缝线路规范(送审稿)与德国规范中线路纵向阻力规定取值计算，仅列出梁体温升15 ℃时2种桥型的钢轨伸缩力，如表1所示。

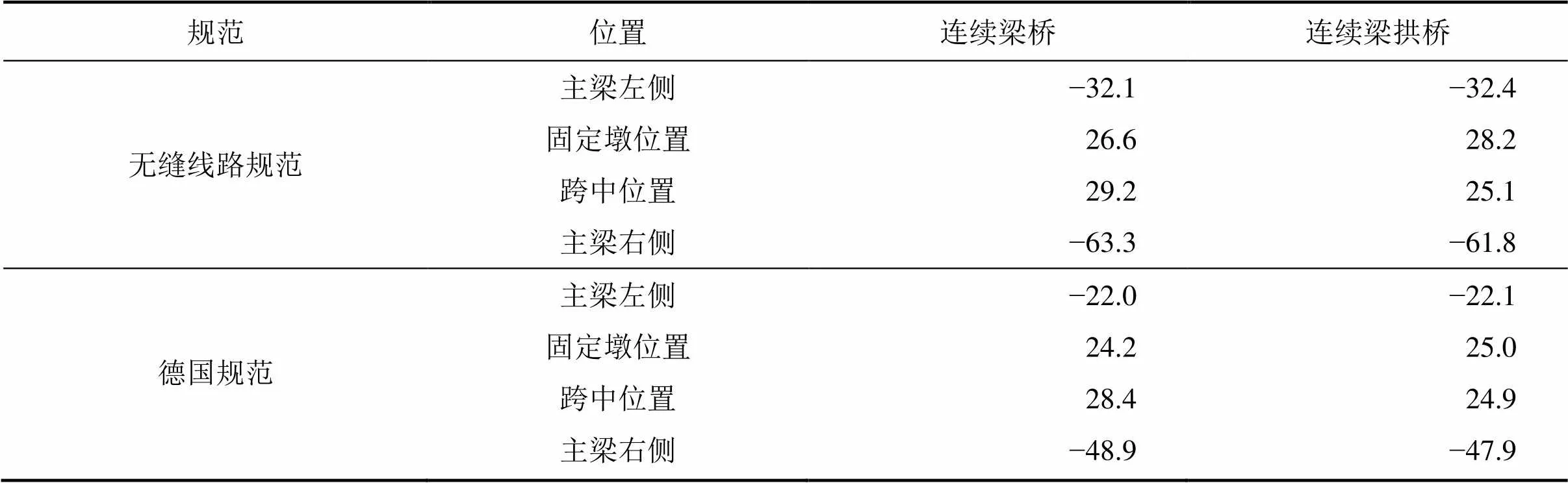
表1 梁体升温15 ℃对钢轨伸缩力的影响

分别根据我国无缝线路规范与德国规范规定计算，结果表明：在跨中位置，连续梁桥与梁拱组合桥钢轨伸缩力相差最大，前者比后者分别大14.3%和12.3%；钢轨最大压应力均位于右侧梁端，连续梁桥钢轨最大拉应力比梁拱组合桥分别大2.0%和2.3%；不论连续梁桥还是梁拱组合桥，钢轨最大拉应力均位于固定墩位置，且相差不大。

考虑到我国地域广阔，温度变化差异较大[11]，为了探讨连续梁桥与梁拱组合桥墩顶水平力对梁体温度变化的敏感性差异，分别根据我国铁路无缝线路规范(送审稿)与德国规范规定进行计算，墩顶水平力随温度变化曲线见图3。

1—连续梁拱桥(无缝线路规范)；2—连续梁桥(无缝线路规范)；3—连续梁拱桥(德国规范)；4—连续梁桥(德国规范)。

从图3可知：连续梁桥对梁体温度的敏感性比连续梁拱桥的大。根据我国无缝线路规范计算，连续梁拱桥墩顶水平力在升温0~40 ℃范围内均比连续梁桥的大；随着温度升高，两者差值逐渐减小。而根据德国规范，连续梁桥墩顶水平力随温度变化增长幅度比连续梁拱桥的大，在梁体升温25 ℃以上时，连续梁桥墩顶水平力比连续梁拱桥的大。

2.2 挠曲荷载作用分析

对于大跨度桥梁，列车行经桥上不同位置导致梁体产生不同挠曲位移，从而引起钢轨与梁体间相互作用不同。本文选取典型位置分析列车荷载工况，如表2所示。

表2 列车荷载工况

分析表2中5种工况作用的钢轨应力可知：由于工况四、工况五钢轨最大应力分别与工况二、工况三的基本相同，本文仅列出工况一、工况二和工况三作用下有载侧钢轨与无载侧钢轨应力曲线，取中跨跨中为零点，如图4所示。

梁拱组合桥刚度比连续梁桥的大，活载作用下的挠度较小，梁轨相对位移较小，故梁拱组合桥钢轨挠曲应力比连续梁桥的小。在工况一作用下，钢轨最大拉、压应力分别位于左侧梁端与边跨跨中位置，连续梁拱桥有载侧钢轨压应力比连续梁桥小38.2%，无载侧钢轨压应力比连续梁桥小41.1%。在工况三作用下，连续梁桥与梁拱组合桥钢轨应力均达到最大，最大拉应力分别为11.5和3.6 MPa，最大压应力分别为16.4和8.19 MPa。左侧梁端位置，连续梁桥有载侧与无载侧钢轨应力均比拱桥大67.8%；在跨中位置，分别大87.4%和89.9%。

在不同荷载工况作用下，连续梁桥与梁拱组合桥墩顶水平力如图5所示。从图5可见：在工况一与工况三分别作用下，由于荷载作用于固定墩两侧，连续梁拱桥刚度较大，梁体产生的转角较小，所以，连续梁桥墩顶水平力比梁拱组合桥分别大93.2 kN和 116 kN；而在工况二、工况四与工况五作用下，因为梁拱组合桥拱脚对梁体的顶推作用较大，使得墩顶水平力增加，梁拱组合桥墩顶水平力比连续梁桥分别大176.1，94.2和72.8 kN。

(a) 工况一；(b) 工况二；(c) 工况三

2.3 列车制动作用分析

固定墩的位置对钢轨制动力影响较大，本文分列车左侧驶入制动与右侧驶入制动这2种工况，钢轨制动力最大值见表3。

图5 活载对墩顶水平力的影响

表3 钢轨制动力最大值

钢轨制动力最大值位于桥梁两端。从表3可知：对于同向驶入的列车制动作用，连续梁桥与连续梁拱桥钢轨制动力基本相等；列车左侧驶入时，钢轨最大拉应力比右侧驶入时小22.3%，而钢轨最大压应力比右侧驶入时大14.1%。

3 其他影响因素分析

3.1 钢轨断轨分析

降温作用下钢轨最大伸缩力位于桥梁梁端，故分别假设断缝出现在梁左端、固定墩处、梁右端，按照主梁降温15 ℃计算[13]。钢轨折断位置不同时钢轨纵向位移比较结果见图6。

钢轨分别在右侧梁端、固定墩、左侧梁端断开时，连续梁桥钢轨伸缩位移分别为2.58，1.97和1.96 cm，梁拱组合桥伸缩位移分别为2.55，1.90和1.89 cm。钢轨在左侧梁端位置与固定墩位置处断开相比，左侧断开时，连续梁桥梁轨相对位移最大值减小33.3%，连续梁拱桥减小34.6%。故对连续梁桥或连续梁拱桥，若设置伸缩调节器，则建议设置在左侧梁端。

主梁变化对两类桥梁断缝影响均显著，当主梁降温达到40 ℃时，连续梁桥梁端断缝可达到6.4 cm，连续梁拱桥梁端断缝可达6.7 cm。

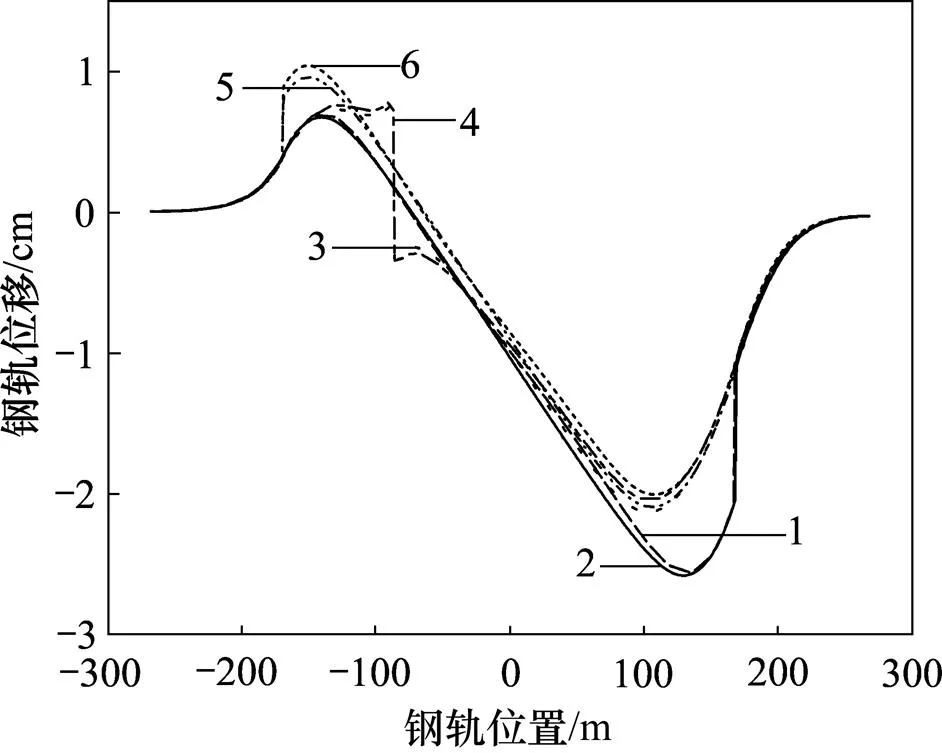
1—连续梁桥(右侧断开)；2—连续梁拱桥(右侧断开)；3—连续梁桥(固定墩断开)；4—连续梁拱桥(固定墩断开)；5—连续梁桥(左侧断开)；6—连续梁拱桥(左侧断开)。

3.2 基础不均匀沉降作用分析

基础不均匀沉降引起钢轨应力包络图见图7。从图7可见：梁拱组合桥左侧梁端钢轨拉应力比右侧拉压力小49.2%，而连续梁桥左右梁端拉应力相差不大；在梁端位置，连续梁桥钢轨应力梁拱组合桥的大；而在跨中位置，前者拉、压应力比后者分别小60.9%和96.9%。

1—连续梁拱桥拉应力；2—连续梁拱桥压应力；3—连续梁桥拉应力；4—连续梁桥压应力。

3.3 收缩徐变作用分析

假设桥梁建成不考虑铁路养护以及列车运行对轨道长期荷载的放散作用，计算铺轨1，10，20，30和40 a后的钢轨最大应力，见图8。

1—连续梁拱桥；2—连续梁桥。

从图8可见：连续梁桥与梁拱组合桥收缩徐变对钢轨影响基本相同，在30 a左右时，前者比后者大1.3%。

4 结论

1) 根据无缝线路规范与德国规范纵向阻力进行计算，梁桥与拱桥钢轨伸缩力最大值均基本相等，在跨中位置，前者比后者分别大14.3%和12.3%。

2) 在最不利挠曲工况下，连续梁桥有载侧与无载侧钢轨挠曲应力最大值比梁拱组合桥均大67.8%；检算挠曲作用墩顶水平力时，建议连续梁桥按照边跨布满加载；梁拱组合桥按照固定墩左右两侧加载。

3) 连续梁桥断轨时钢轨伸缩位移比连续梁拱桥的大；若需要对2类桥型设置伸缩调节器，建议均设置在离固定墩较近的梁端位置，这样可以有效减小钢轨位移与桥台处钢轨受力。

4) 在相同方向列车制动、桥梁收缩徐变作用下，2类桥梁钢轨应力随钢轨纵向变化规律基本一致；在基础沉降作用下，连续梁桥钢轨最大拉应力比梁拱组合桥的最大拉应力大49.2%。

[1] BATTINI J M, MAHIR U K. A simple finite element to consider the non-linear influence of the ballast on vibrations of railway bridges[J]. Engineering Structures, 2011, 33(9): 2597−2602.

[2] RUGE P, BIRK C. Longitudinal track–bridge interaction due to sudden change of coupling interface[J].Computers & Structures, 2007, 85(7/8): 458−475.

[3] 陈嵘, 马旭峰, 田春香, 等. 连续梁桥上单元板式无砟轨道纵向变形的控制[J].铁道工程学报, 2016(1): 58−64. CHEN Rong, MA Xufeng, TIAN Chunxiang, et al. Longitudinal deformation control of unit slab nonballast track on continuous beam bridge[J]. Journal of Railway Engineering Society, 2016(1): 58−64.

[4] 蔡小培, 高亮, 孙汉武, 等. 桥上纵连板式无砟轨道无缝线路力学性能分析[J]. 中国铁道科学, 2011, 32(6): 28−33. CAI Xiaopei, GAO Liang, SUN Hanwu, et al. Analysis on the mechanical properties of longitudinally connected ballastless track continuously welded rail on bridges[J]. China Railway Science, 2011, 32(6): 28−33.

[5] YAN Bin, DAI Gonglian. Seismic pounding and protection measures of simply-supported beams considering interaction between continuously welded rail and bridge[J]. Structural Engineering International, 2013, 23(1): 61−67.

[6] TB 10015—2012, 铁路无缝线路设计规范[S]. TB 10015—2012, Code for design of railway continuously welded rail[S].

[7] Germany DS899/59, Special procedures on railway Shinkansen bridge[S].

[8] 李艳. 大跨斜拉桥上无缝线路纵向力的变化规律研究[J]. 铁道工程学报, 2012(10): 42−46. LI Yan. Study on variation rules of longitudinal force of continuous welded rails on long-span cable-stayed bridge[J]. Journal of Railway Engineering Society, 2012(10): 42−46.

[9] 徐庆元, 陈秀方, 李树德. 高速铁路桥上无缝线路纵向附加力研究[J]. 中国铁道科学, 2006, 27(3): 8−12. XU Qingyuan, CHEN Xiufang, LI Shude. Study on the additional longitudinal forces transmission between continuously welded rails and high-speed railway bridges[J]. China Railway Science, 2006, 27(3): 8−12.

[10] LIU Wenshuo, DAI Gonglian, HE Xuhui. Sensitive factors research for track-bridge interaction of Long-span X-style steel-box arch bridge on high-speed railway[J]. Journal of Central South University, 2013, 20(11): 3314−3323.

[11] 吴亮秦, 吴定俊, 李奇. 城市轨道交通桥梁列车制动力试验研究[J]. 铁道学报, 2012, 34(3): 88−93. WU Liangqin, WU Dingjun, LI Qi. Experimental study on braking force for urban rail transit bridge[J]. Journal of the China Railway Society, 2012, 34(3): 88−93.

[12] BS EN 1992−1−1:2004 Eurocode 2, Design of concrete structure. Part 1-1: general rules and rules for buildings[S].

[13] 王平, 陈小平. 桥上无缝线路钢轨断缝计算方法的研究[J]. 交通运输工程与信息学报, 2004, 2(2): 47−52. WANG Ping, CHEN Xiaoping. Study on the calculation methods of rail break of CWR on bridge[J].Journal of Transportation Engineering and Information, 2004, 2(2): 47−52.

(编辑 陈灿华)

Comparison of track-bridge interaction between long-span continuous girder bridge and continuous arch bridge

DAI Gonglian1, LIU Yao1, 2, LIU Wenshuo1

(1. School of Civil Engineering, Central South University, Changsha 410083, China;2. Hunan University Design Institute Co. Ltd., Changsha 410082, China)

Different track-bridge interactions on continuous girder bridge and continuous arch bridge were studied. Taking the (82.9+172.0+82.9) m span arrangement as an example, two models were established by considering track− girder−pier−understructure and track−arch−derrick−pier−understructure−girder, respectively. The longitudinal forces distributions of CWR and horizontal forces at pier top were systematically analyzed under the actions of bending, braking, thermal effect, shrinkage and creep, etc. Furthermore, the relevant design parameters were also discussed. The results show that adopting the longitudinal resistance specified in Chinese code and German code, the expansion stresses of rail in continuous girder bridge are 2.0% and 2.3% larger than those of continuous arch bridge, and the bending stress of rail with load and without load at continuous girder bridge is 67.8% larger than that of the continuous arch bridge. The temperature variation and broken rail position have significant effect on the broken rail force. The stresses of rail in two bridges are basically identical under the train braking and the creep and shrinkage of concrete. For the understructure, continuous girder bridge is more sensitive to beam temperature, and the longitudinal force of pier in continuous arch bridge is 176.1 kN larger than that of the continuous girder bridge under the action of running train.

railway bridge; continuous girder bridge; continuous arch bridge; track-bridge interaction; continuously welded rail

10.11817/j.issn.1672-7207.2017.01.031

U213.912

A

1672−7207(2017)01−0233−06

2016−01−06；

2016−03−06

国家自然科学基金资助项目(51378503)；中国博士后科学基金资助项目(2015M570687) (Project (51378503) supported by the National Natural Science Foundation of China; Project(2015M570687) supported by China Postdoctoral Science Foundation)

刘文硕，博士，讲师，从事高速铁路桥梁−轨道系统相互作用等研究；E-mail: liuwenshuo@csu.edu.cn