k-树及其邻点可区别全染色

张 琛，李红霞

(陇东学院数学与统计学院，甘肃庆阳745000)

k-树及其邻点可区别全染色

张 琛，李红霞

(陇东学院数学与统计学院，甘肃庆阳745000)

G是一个简单图，G的一个全染色f是指使相邻顶点和相邻边着不同颜色且每条关联边与它的顶点着以不同颜色的全染色。设f为图G一个全染色，对任意x∈V(G)，用C(x)表示在f下顶点的颜色以及与x关联的边的颜色所构成的集合。若任意uv∈E(G)，u≠v，有C(u)≠C(v)，则称f是图G的邻点可区别的全染色，该问题的主要目的是确定图G的邻点可区别全色数。基于树的基本结构，构造了一种新的图类—k-树，讨论并给出了两类k-树S(n,1)，S(n,2)的邻点可区别全色数。

树；k-树；邻点可区别全染色；邻点可区别全色数

凡有二元关系的系统，图论均可提供一种数学模型——图。要讨论客观世界中某些具体事物间的联系，则用顶点代表事物，用边表示各事物间的二元关系；如果所讨论的事物之间有某种二元关系，我们就把相应的顶点连成一条边。这种由顶点及连接这些顶点的边所组成的图就是所研究的对象。在图论众多的图类中，树是非常重要的一类图，它是最简单的连通图，许多问题对一般连通图未能解决或者没有简单的方法，而对于树，则已圆满解决，且方法较为简单。受文献[1]启发，本文基于树的基本结构，构造了一种新的图类——k-树。

图论研究中的一个重要方向是图的染色问题。许多实际问题都可以转化为图的染色模型，例如资源配置、印刷电路布线、加载问题、频率分配等。1985年，HararyF等人开始研究图的点可区别的一般边染色；ChartrandG，JacobsonM，LehelJ等人于1986年研究图的可允许的一般边染色(即顶点被关联边的颜色之和可区别的一般边染色，所使用的颜色是从1开始的相继的正整数)所需要的颜色的最少数目即图的非正规强度；BurrisAC，SchelpRH则于1993年提出图的点可区别正常边染色。自2002年以来，张忠辅教授相继提出图的邻点可区别正常边染色，邻点可区别正常全染色，点可区别正常全染色等新的图染色概念之后，图的可区别染色受到越来越多学者的重视。特别是2004年，在全染色的基础上，张忠辅，陈祥恩等人提出了邻点可区别的全染色这一概念(见参考文献[2]，此文荣获2008年度“中国百篇最具影响国内文章”。该文的英文版见参考文献[3])，使得图论界产生了许多更有趣的问题(如子图的邻点可区别全色数不一定比母图小)，并且已得到了一些有价值的成果[4-10]。因此，本文也将对k-树图的邻点可区别全染色进行讨论。

1 定义及引理

本文所考虑的图均为有限、无向的简单图。Δ(G)，d(v)分别表示图G的最大度和图G中顶点v的度。其它术语及符号参照文献[2]。

定义1.1[11]一个n阶图Tn是树当且仅当Tn中任意两个不同顶点之间有且只有一条路连接。

定义1.2[2]含有n-1个悬挂点的n阶树Tn，称为n阶星Sn。

定义1.3[11]对图G(V(G),E(G))，k是正整数，S是k元集，f是从V(G)∪E(G)到S的映射。如果

1)∀uv,vw∈E(G)，u≠w，有f(uv)≠f(vw)， 2)∀uv∈E(G)，有f(u)≠f(v)，f(u)≠f(uv)，f(uv)≠f(v)，

定义1.4[2]对图G(V(G),E(G))，t是正整数，S是t元集，f是从V(G)∪E(G)到S的映射。如果

1)f是图G的正常全染色，

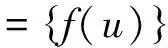
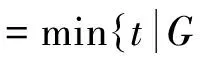
由定义可知：一个图G的邻点可区别全染色，一定是图G的正常全染色，因此显然有，χt(G)≤χat(G)。又由于一个图的邻点可区别全色数等于它的各个分支的邻点可区别全色数的最大值，因此以下均考虑连通图。

引理1.1[2]对任一图G，有

ⅰ)χat(G)≥Δ(G)+1；

ⅱ)当图G具有两个相邻的最大度点时，χat(G)≥Δ(G)+2。

引理1.2[2]若Tn为n阶树(n≥4)，则：

引理1.3[2]若Sn为n阶星(n≥4)，则χat(Sn)=n。

在文献[2,3]中，张忠辅等人提出了关于邻点可区别全色数的猜想：对n阶图G，有χat(G)≤Δ(G)+3。

本文将证明该猜想对于两类k-树的邻点可区别全色数是成立的。首先我们给出k-树图的定义。

定义1.5 对n阶树Tn，k为正整数，若图G的顶点集合与边集合分别为：

V(G)=V(Tn)∪{v1,v2,…,vk}={u1,u2,…un,v1,v2,…,vk}，

E(G)=E(Tn)∪{uiv1,uiv2,…,uivn,i=1,2,…,n}，

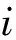
若n阶树Tn为n阶星Sn，则当k=1时，该类k-树记为S(n,1)；当k=2时，该类k-树记为S(n,2)。图1为n=4，n=5时两类k-树的结构模式。

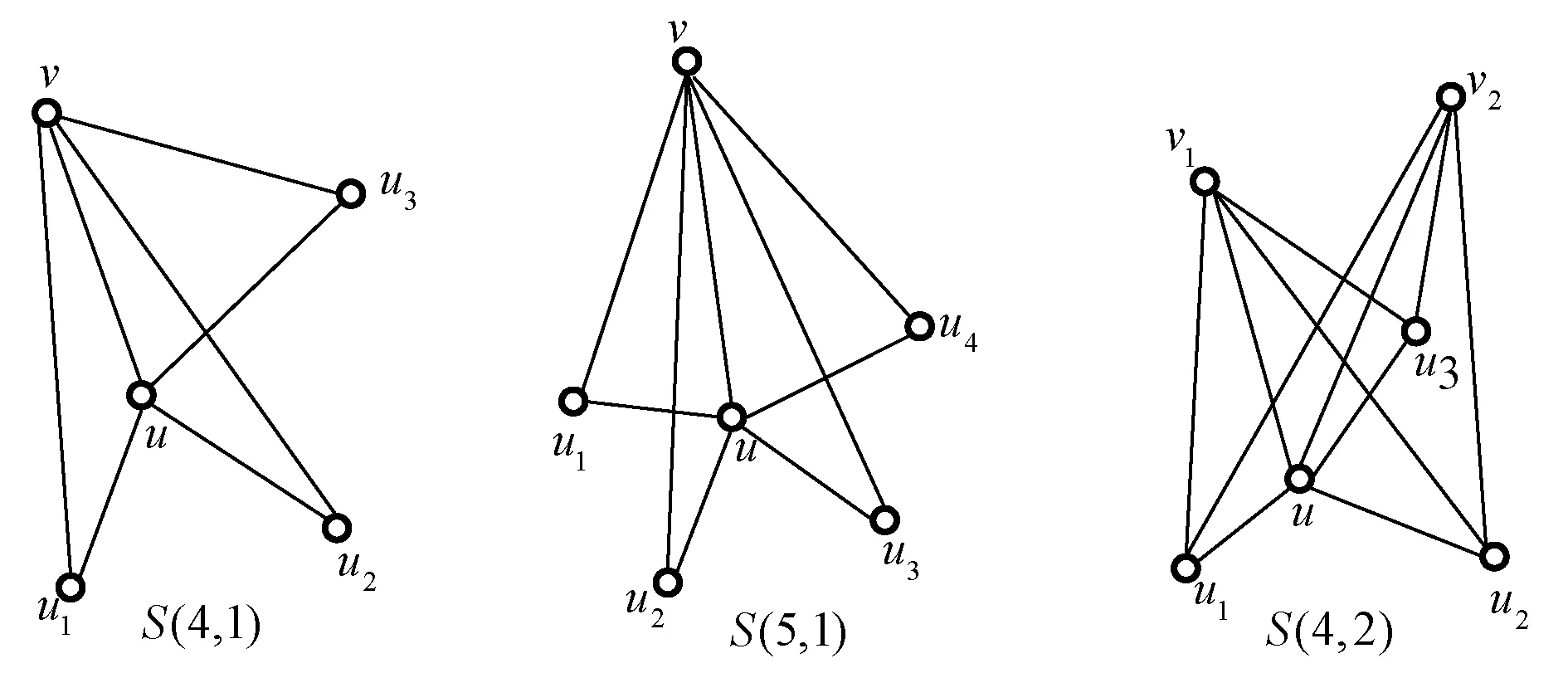
图1 两类k-树的结构模式

文中确定了S(n,1)与S(n,2)的邻点可区别全色数。①当n=1时，S(n,1)与S(n,2)均为一条路，文献[2]中得到χat(P2)=χat(S(1,1))=3，χat(P3)=χat(S(1,2))=3。②当n=2时，S(n,1)为圈C3，同样在文献[2]中已得到χat(C3)=4；S(n,2)为完全图K4的一个子图，易得χat(S(2,2))=4，图2(a)给出了S(2,2)的一种邻点可区别全染色。③当n=3时，S(3,1)与S(2,2)同构；S(3,2)是最大度为4的广义Halin图，易得χat(S(3,2))=5，图2(b)给出了S(3,2)的一种邻点可区别全染色，同时该结论也支持文献[12]中关于广义Halin图的邻点可区别全染色猜想。

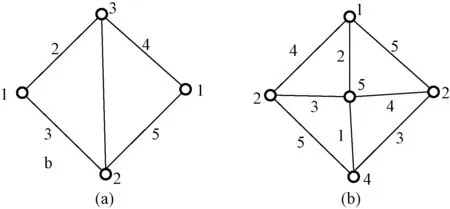
图2 两类k-树的染色方案

故以下不妨设n≥4。

2 主要结果

定理2.1 对k-树S(n,1)，n≥4，有χat(S(n,1))=n+2。

证明 若记

V(S(n,1))={u,u1,u2,…,un-1,v}，

E(S(n,1))={uui,uiv,uv,i=1,2,…,n-1}，则u与v为S(n,1)中唯一一对相邻的最大度点，且d(u)=d(v)=n。

因为Δ(S(n,1))=n且S(n,1)中有两个相邻的最大度点，由引理2.1可知：

χat(S(n,1))≥Δ(S(n,1))+2=n+2，

以下讨论S(n,1)可用n+2种色进行其邻点可区别全染色。

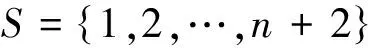
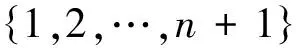
f(ui)=i，i=1,2,…,n-1，f(u)=n+1，

f(uui)=i+1，i=1,2,…n-1。

其次对顶点v及与顶点v关联的边正常染色，

f(v)=n+2，f(uv)=1，

f(uiv)=i+2，i=1,2,…,n-2，f(un-1v)=2。

在上述染色方案中，

C(u)={1,2,…,n,n+1}，C(v)={1,2,…,n,n+2}，

C(ui)={i,i+1,i+2}，i=1,2,…,n-2，C(un-1)={2,n-1,n}。

下面说明染色方案f是S(n,1)的邻点可区别全染色。

定理2.2 对k-树S(n,2)，n≥4，有χat(S(n,2))=n+2。

证明 若记

V(S(n,2))={u,u1,u2,…,un-1,v1,v2}，

E(S(n,2))={uui}∪{uiv1,uv1}∪{uiv2,uv2}，其中i=1,2,…,n-1，

则u为S(n,1)中唯一的最大度点，且d(u)=n+1。

因为Δ(S(n,2))=n+1且S(n,2)中没有相邻的最大度点，由引理1.1可知：

χat(S(n,2))≥Δ(S(n,2))+1=n+2，

以下讨论S(n,2)可用n+2种颜色进行其邻点可区别全染色。

令S={1,2,…,n+2}，用S中的颜色构造S(n,2)的染法f，如下：

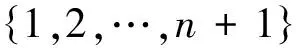
f(ui)=i，i=1,2,…,n-1，f(u)=n+1，

f(uui)=i+1，i=1,2,…,n-1。

其次对顶点v1及与顶点v1关联的边正常染色，

f(v1)=n+2，f(uv1)=1，

f(uiv1)=i+2，i=1,2,…,n-1。

再次对顶点v2及与顶点v2关联的边正常染色，

f(v2)=n，f(uv2)=n+2，

f(u1v2)=n+1，f(uiv2)=i-1，i=2,3,…,n-1。

在上述染色方案中，

C(u)={1,2,…,n+2}，

C(v1)={1}∪{3,4,…,n+2}，C(v2)={1,2}∪{4,5,…,n+2}，

C(u1)={1,2,3,n+1}，C(ui)={i-1,i,i+1,i+2}，i=2,3,…,n-1。

下说明染色方案f是S(n,2)的邻点可区别全染色。

根据定理2.1和2.2的证明，我们有一个猜想：k-树S(n,k)，k为正整数，n≥4，有χat(S(n,k))=n+2。对该猜想的证明可沿用定理2.1和2.2的证明方式，但叙述是困难的，所以在以后的研究中我们将考虑借助于机器证明。

[1]马德山,刘林忠,张忠辅.1-树图的邻强边染色[J].数学研究与评论,2000(2):299-305.

[2]张忠辅,陈祥恩,李敬文,等.关于图的邻点可区别全染色[J].中国科学A辑(数学)，2004(5):574-583.

[3]ZHANGZhong-fu,CHENXiang-en,LiJingwen,等.Onadjacent-vertex-distinguishingtotalcoloringofgraphs[J].中国科学A辑(英文版)，2005(3):289-299.

[4]CHENXiang-en,ZHANGZhong-fu.Adjacent-vertex-DistinguishingtotalchromaticnumberonMycielski'sgraphsofseveralkindsofparticulargraphs[J].JournalofLanzhouUniversity(NaturalScience),2005,41(2):117-122.

[5]CHENXiang-en,ZHANGZhong-fu.Adjacent-Vertex-distinguishingTotalchromaticnumberofPm×Kn[J].数学研究与评论，2006,26(3):489-494.

[6]CHENXiang-en,ZHANGZhong-fu.Adjacent-vertex-distinguishingtotalchromaticnumberon2-connectedouterplanegraphwithΔ(G)≤4[J].兰州大学学报(自然科学版)，2006,49(6):703-708.

[7]陈祥恩,张琛.直积图的邻点可区别全染色[J].兰州理工大学学报，2008(2):137-140.

[8]张琛,陈祥恩,刘信生.多重Mycielski图的邻点可区别全染色[J].西北师范大学学报(自然科学版)，2007(6):22-26.

[9]张琛,张如清,吕卫东.K2s×K2t的邻点可区别全染色[J].数学的实践与认识,2012(20):213-216.

[10]张琛,王欣欣.K2n-1×K2n+1的邻点可区别全染色[J].佳木斯大学学报(自然科学版),2013,31(3):464-466.

[11]BONDYJA,MURTYUSR.Graphtheorywithapplications[M].NewYork:Macmillan,1976:91-134.

[12]陈祥恩.图的可区别染色引论[M].北京:中国科学技术出版社,2015:146-246.

【责任编辑 朱世广】

The Adjacent Vertex-distinguishing Total coloring ofk- tree

ZHANG Chen，LI Hong-Xia

(SchoolofMathematicsandStatistics,LongdongUniversity,Qingyang745000,Gansu)

LetGbe a simple graph. A total coloring f ofGis called an total coloring if no two adjacent vertices and no two adjacent edges ofGreceive the same color, and no edge of receives the same color as one of its endpoints. For an total coloringfof a graph and any vertex ofG, letC(x) denote the set of colors of vertex x and of the edges incident withx, we callC(x) the color set ofx. IfC(u)≠C(v) for any two adjacent vertexesuandvofV(G), then we say thatfis a adjacent vertex-distinguishing total coloring ofG. The main purpose of this problem is to determine the adjacent vertex-distinguishing total chromatic number ofG. In this paper, a new graph,k- tree, is constructed on the base of the structure of the tree. The adjacent vertex-distinguishing total chromatic number onk- tree are obtained for some special graphs, such asS(n,1) andS(n,2).

tree;k- tree; adjacent vertex-distinguishing total coloring; adjacent vertex-distinguishing total chromatic number

1674-1730(2017)01-0011-04

2016-06-13

甘肃省高等学校科研项目《模糊图在网络优化中的应用研究》(2015A-144)

张 琛(1983—)，女，甘肃庆阳人，讲师，硕士,主要从事图的染色理论研究。

O

A