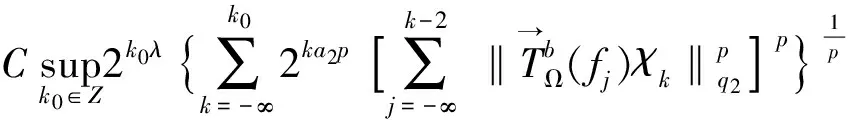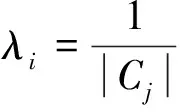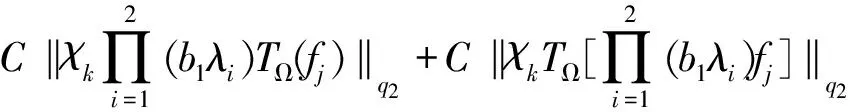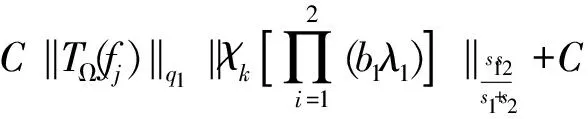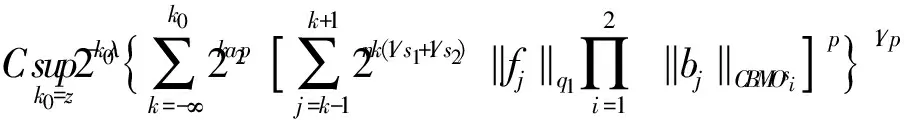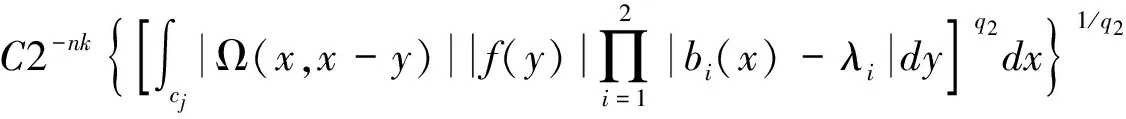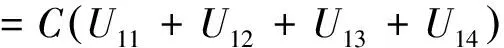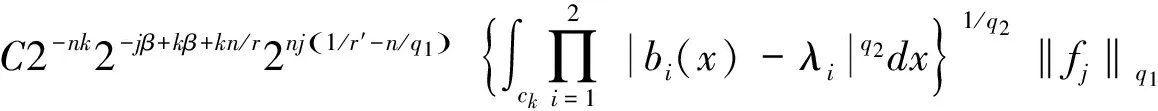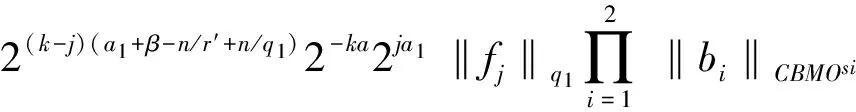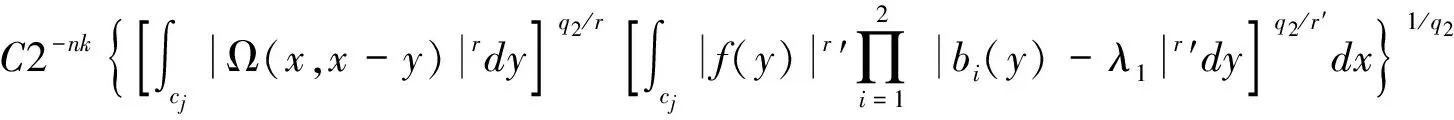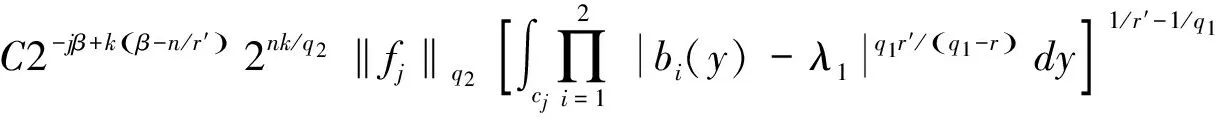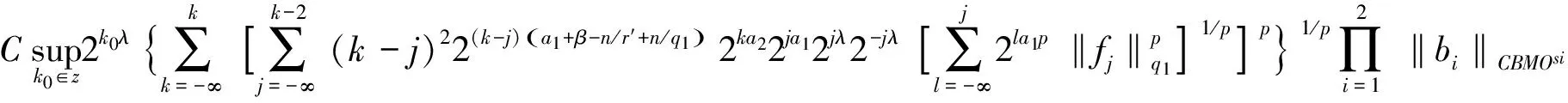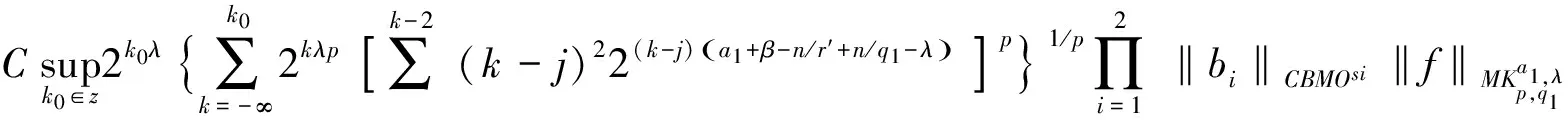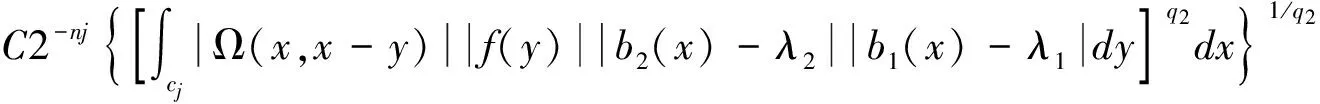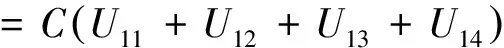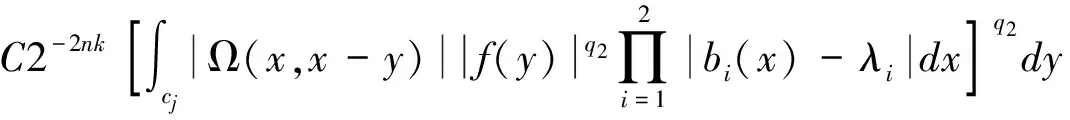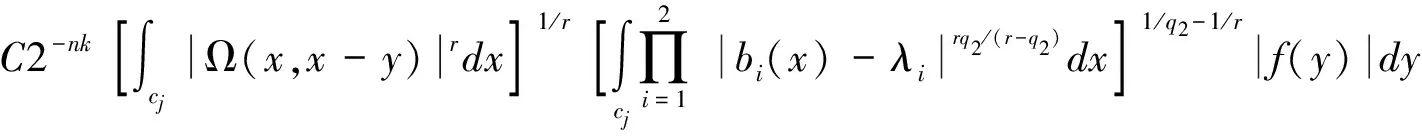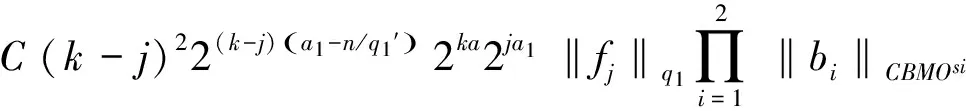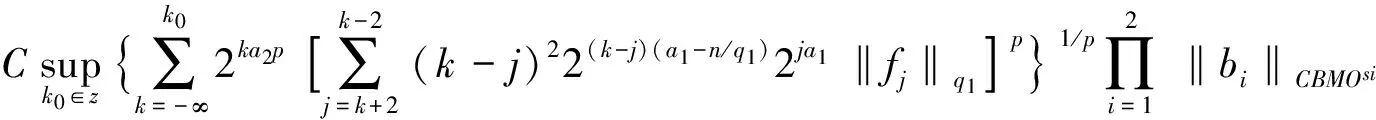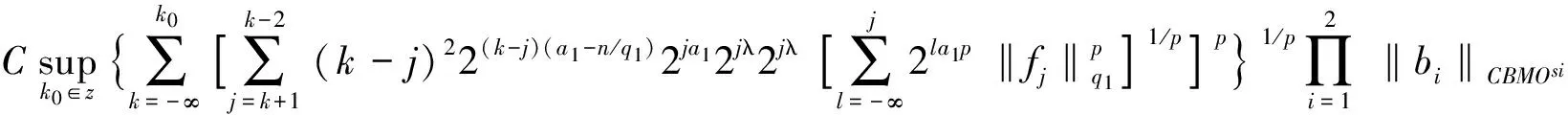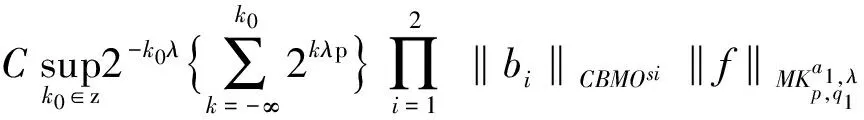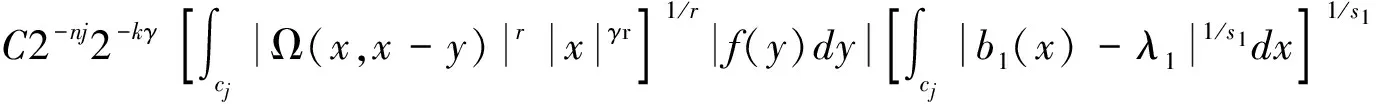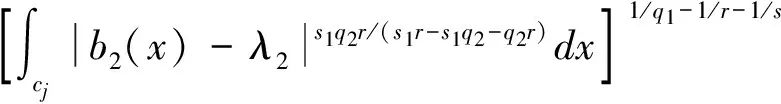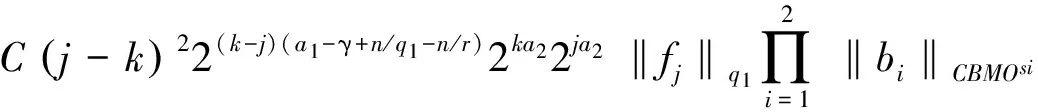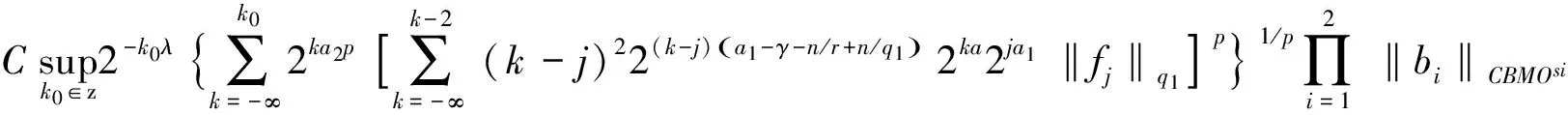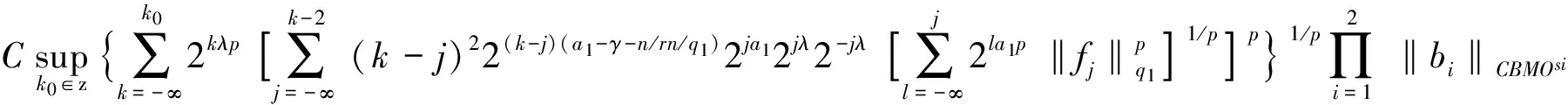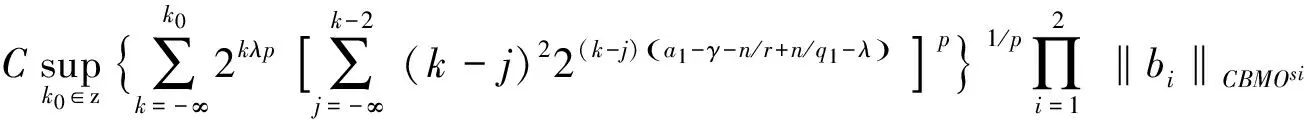变量核奇异积分交换子在齐次Morrey-Herz空间上的有界性
崔建斌,邵旭馗
(陇东学院数学与统计学院,甘肃庆阳745000)
变量核奇异积分交换子在齐次Morrey-Herz空间上的有界性
崔建斌,邵旭馗
(陇东学院数学与统计学院,甘肃庆阳745000)
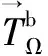
Carlderón-Zygmund奇异积分;交换子;齐次Morrey-Herz空间;变量核
设Sn-1为Rn(n≥2)中的单位球面,Ω(x,y)∈L∞(Rn)×Lr(Sn-1)(r≥1)是零次齐次函数且满足
(1)
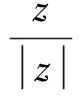

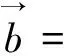

(2)

定义1 设1 其中 其中 下面先给出一些必要的记号: 本文的主要结果为 a1和q1满足下列条件之一: 定理1的证明 下面只考虑λ>0,且只给出当m=2,0 根据Minkowski不等式有 =C(I1+I2+I3). +C‖χk(b1λ1)TΩ(b2λ2)fj‖q2+C‖χk(b2λ2)TΩ(b1λ1)fj‖q2 从而 下面分两种情况来估计I1和I3,先考虑情况(i),对I1进行估计: 注意到r≤q2 由引理1和引理2知: 用类似的方法,可以得到 由Hölder不等式得到 因此,得 于是 类似于U11和U12的估计,运用Hölder不等式和引理1即可得到以上估计。 下面讨论情况(ii)。先估计I1。根据引理2,Minkowski不等式和Hölder不等式,可得 类似地,得到 从而得到I1的估计: 为了估计I3,取γ>1使得α1>γ+n/r-n/q1+λ>-1/r+nr-n/q1+λ则有 类似地,可以得到U32,U33,U34的估计。于是 综合I1,I2和I3的估计,定理1得证。 [1]SteinEM.OnthefunctionofLittlewood-Paley,LusinandMarcinkiewicz[J].TransAmerMathsoc,1958,88:430-466. [2]LuS,WuQ.CBMOestimatesforcommutatorandmultilinealssingularsintegrals[J].Math.Nachr, 2004,276:75-88. [3]林燕.粗糙核分数次积分交换子及多线性算子的CBMO估计[J].北京师范大学学报,2007,43:120-126 [4]邵旭馗,陶双平.带变量核的Marcinkiewicz积分交换子的加权Lipschitz估计[J].系统科学与数学,2012,32(7):915-921. [5]邵旭馗,陶双平,王素萍.带变量核的参数型Marcinkiewicz积分在弱Hardy空间上的有界性[J].应用数学,2013,42(1):177-181. [6]陶双平,边敏静.粗糙核奇异积分算子在加权Companato空间上的有界性[J].兰州大学学报(自然科学版),2011,47(8):91-98. [7]DingY,FanD,PanY.BoundednessofMarcinkiewiczintegralswithHardyspacekemel[J].ActaMathSciSerB,2000,16:593-600. [8]Lu.S,YangD.ThecentralCBMOspacesandlittltwood-Palyoperators[J].ApproxTheoryanditsApp.1,1995,11:72-94. [9]陶双平,邵旭馗.带变量核的Marcinkiewicz积分在齐次Morrey-Herz空间上的有界性[J].兰州大学学报(自然科学版),2010,46(6):102-107. [10]张晓瑾,刘瑞芹,文小艳.带粗糙核的积分算子在齐次空间上的有界性[J].淮阴工学院学报,2009,18(3):27-34. 【责任编辑 朱世广】 The Boundedness of Singular Integral Commutators with Variable Kernels on Homogeneous Morrey-Herz Spaces CUI Jian-bin, SHAO Xu-kui (SchoolofMathematicsandStatistics,LongDongUniversity,Qingyang745000,Gansu) Carlderón-Zygmund singular integral; commutator; Morrey-Herz space; Variable kernel 1674-1730(2017)01-0006-05 2016-04-20 甘肃省高等学校科研项目《一类变量核奇异积分算子及其交换子的有界性研究》(2015A-147) 崔建斌(1972—),男,副教授,硕士,主要从事数据挖掘与灰色预测研究。 O A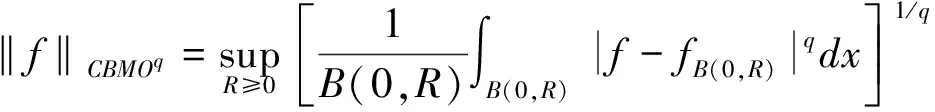
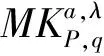


1 主要结果
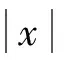
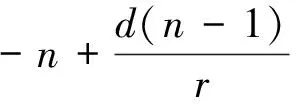
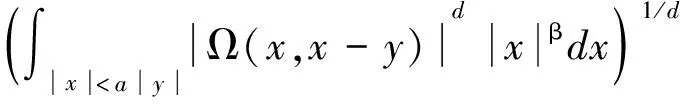
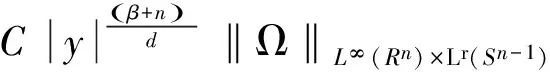
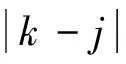


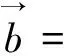

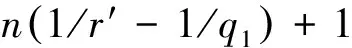
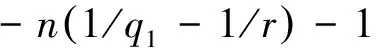
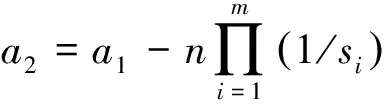
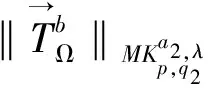
2 定理的证明