Huppert可裂性定理的一个推广*

贾婷婷， 郝成功

(山西大学 数学科学学院， 山西 太原 030006)

Huppert可裂性定理的一个推广*

贾婷婷， 郝成功

(山西大学 数学科学学院， 山西 太原 030006)

研究了一个有限群何时在某个正规子群上可裂的问题， 推广了著名的Huppert可裂性定理， 主要把Huppert可裂性定理中讨论的p-版本推广到π-版本并对其进行了详细的证明， 从而得到一个更为广泛的证明可裂性的判据. 其证明引用了经典的Gaschütz可裂性定理， 运用了传输同态， 采用了由特殊到一般的证明思路. 最后， 作为对该定理的实际应用， 给出了若干经典的传输定理的统一的简化证明.

可裂性； 正规子群；π-商群； 交换π-商群

0 引 言

本文只考虑有限群， 所使用的符号和术语大多是标准的， 可参考Isaacs的群论教程[1-2]， 对于正规p-补的一些结论可参见文献[3]. 特别地， 本文约定p为某个素数，π为某个非空的素数集，π′为π在全体素数集中的补集. 给定正整数m， 记π(m) 为m的全体素因子. 称群G为π-群， 如果|G|的每个素因子均属于π， 称x∈G为一个π-元， 如果〈x〉是π-群. 当π={p}， 则π-群成π′-群分别简称为p-群或p′-群，p-元和p′-元类似定义.

设G为群，N◁G， 若存在H≤G， 满足NH=G且N∩H=1， 则称H为N在G中的一个补， 也称G在正规子群N上是可裂的. 熟知判别群在一个正规子群上的可裂性是有限群理论中的一个重要问题， 至今已获得了很多研究成果， 其中特别著名的是Schur-Zassenhaus定理[4]， Gaschütz定理[4]， 以及Huppert定理[5]. 这些经典定理有很多的推广和应用， 例如对可裂扩张的Schur乘子群， 自同构群和置换表示等的研究， 参见文献[6-10]， 显然这类问题具有广泛的应用前景和很大的研究价值. 特别地， 可裂性判别问题在有限群的传输理论中的许多著名定理的设计和证明中， 均发挥着极其重要的作用.

本文将研究Huppert的一个著名的可裂性定理. 为此先固定一些符号和记法. 对有限群G， 记Oπ(G)为G中所有π′-元所生成的子群， 并且Aπ(G)=Oπ(G)G′， 显然都是G的特征子群， 使得G/Oπ(G)和G/Aπ(G)分别是G的最大π-商群和最大交换π-商群. 当π={p}时， 则上述两个子群分别简记为Op(G)和Ap(G). 以下是Huppert可裂性定理， 证明可见定理6.16[5].

Huppert可裂性定理. 设G为群，N◁G，H≤G， 使得G=NH且J=N∩H. 如果K≤J为H的一个正规子群， 使得J/K为交换p-群， |G∶H|为p′-数且Op(N)=N， 则J/K在H/K中有补.

上述Huppert定理有很多应用， 例如， 可给出著名的Tate传输定理[11]的一个群论证明， 避免了原始证明中的上同调技术. 然而， Huppert定理只处理了单个的素数p， 并没有涉及到素数集合π， 而很多经典的传输定理都涉及到素数集合π， 这就极大地限制了Huppert定理的应用范围.

本文主要结果是给出了上述Huppert可裂性定理的一个推广， 不仅得到了其π-版本， 而且给出的证明更加简明， 可替代Huppert可裂性定理原始的复杂证明.

定理 1 设G为群，N◁G且H≤G. 令J=N∩H. 如果K≤J是H的正规子群， 且满足：

1) 交换条件：J/K为交换群；

2) 互素条件： (|J∶K|, |G∶H|)=1；

3)π-商群条件：N=Aπ(N)， 其中π=π(J/K).

则J/K在H中有补， 即存在子群X使得JX=H且J∩X=K.

作为定理1的应用， 本文将直接推出若干著名的经典传输定理.

1 证明及应用

为了证明定理1， 需要引用下述经典的Gaschütz可裂性定理[12].

Gaschütz可裂性定理 设Γ为群，A是Γ的交换正规子群. 如果A≤U≤Γ， 且(|A|,|Γ∶U|)=1， 则A在Γ中有补当且仅当A在U中有补.

证明 见定理3.3.2[4].

定理 1 的证明 根据所给条件及所证结论， 不妨设G=NH. 此时G/N≅H/J， 故存在自然的满同态

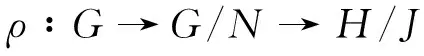
使得Kerρ=N. 因为K≤J， 所以有明显的满同态σ∶H/K→H/J，hK|hJ，h∈H.

考虑H/K与G的外直积H/K×G， 令

易知Γ是H/K×G的子群. 设α∶Γ→G为从Γ到G的自然投射， 则α是一个满同态. 再令A=Kerα， 从定义可知

且A≅J/K.

断言A在Γ中有补. 令U=α-1(H)， 则U={(hK,h′)|h∈H,h′∈hJ}， 且有|Γ∶U|=|G∶H|. 记D={(hK,h)|h∈H}， 则U=AD且A∩D=1. 又由A◁Γ可得A◁U， 表明D是U中正规子群A的补. 已知A≅J/K是Γ的变换正规子群，A≤U≤Γ， 且(|A|,|Γ∶U|)=(|A|,|G∶H|)=1， 因此利用上述Gaschütz定理， 可知A在Γ中有补.

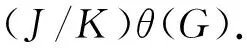
记T=θ(G)∩(J/K)， 只需证T=1. 因为σθ=ρ， 所以

下面是定理1的若干应用， 即重新给出几个经典传输定理的简洁的统一证明. 首先给出Tate著名的传输定理的一个简化证明， 原始证明使用了上同调技术， 见文献[11].

Tate定理 设G为群，P∈Sylp(G)且P≤H≤G， 则G/Op(G)≅H/Op(H)当且仅当G/Ap(G)≅H/Ap(H).

证明 必要性是显然的， 因此只证充分性. 令J=H∩Op(G)， 只需证J=Op(H). 显然有Op(H)≤J， 故假设Op(H)

下面结论是S.Gagola和I. Isaacs[13]的一个新结果， 最初想法是给出Tate定理的一个简洁的群论证明， 但对传输同态的像做了精细的分析.

Gagola-Isaacs定理 设G为群，P∈Sylp(G)且P≤H≤G， 则G/Ap(G)同构于H/Ap(H)的一个直积因子.

证明 首先断言Ap(H)覆盖Ap(G)/Op(G). 由(|G∶Op(G)|,|G∶H|)=1， 知G=HOp(G). 注意到Op(G)Ap(H)◁Op(G)H， 故

为交换p-群， 表明Ap(G)≤Op(G)Ap(H)， 但反包含是显然的， 因此Ap(G)=Op(G)Ap(H). 即断言成立.

令J=H∩Ap(G),K=Ap(H)， 则K≤J,G/Ap(G)≅H/J. 由定义，H/K是变换群， 故J/K交换. 又因为P≤H≤G， 所以|G∶H|是p′-数， 而J/K是p-群， 故(|J∶K|,|G∶H|)=1. 另外显然Ap(G)=Ap(AP(G)). 由定理 1 知存在子群Ap(H)≤X≤H满足H/K=(J/K)×(X/K). 又因X/K≅H/J， 故H/K=(J/K)×(H/J). 因此G/Ap(G)同构于H/Ap(H)的一个直积因子. 证毕.

以下定理是J. Tate在文献[11]中用上同调方法证明的一个结论， 但其证明较为复杂. 后来P. Roquette在文献[14]中用群论的方法证明了该结果. 下面将使用定理 1 直接证明该定理.

最后给出Suzuki传输定理[15]的一个证明.

Suzuki定理 设G为群，N◁G,H≤G且J=H∩N. 如果|G∶H|为π′-数， 并且J/Oπ(J)≤Φ(H/Oπ(J))， 则Oπ(J)=H∩Oπ(N).

[1]Isaacs I M. Finite group theory[M]. US: American Mathematical Society, 2008.

[2]徐明曜. 有限群初步[M]. 北京： 北京大学出版社， 2008.

[3]Thompson J G. Normalp-complements for finite groups[J]. J. Alg., 1964, 1: 43-46.

[4]Kurzweil H, Stellmacher B. The theory of finite groups[M]. New York: Sringr-Verlag, Inc., 2004.

[5]Huppert B, Blackbum N. Finite group III[M]. New York: Springer-Verlag, 1982.

[6]Haebich W. The multiplicator of a splitting extension[J]. Journal of Algebra, 1977, 44(2): 420-433.

[7]Fan Y, Huang P. The stable automorphism groups of splitting extension of finite groups[J]. Chinese Annals of Mathematics, series A, 2001, 6: 791-796.

[8]Easdown D, Hendriksen M. Minimal permutation representations of semidirect products of groups[J]. Journal of Group Theory, 2016, 19(6): 1017-1048.

[9]秦应兵， 王文娟， 段泽勇. 阿贝尔群被超-(循环或有限)群的可裂扩张(I)[J]. 纯粹数学与应用数学， 2003， 19(2)： 112-118. Qin Yingbing, Wang Wenjuan, Duan Zeyong. Splitting extensions of Abelian by hypercyclic or finite group (I)[J]. Pure and Applied Mathematics, 2003, 19(2): 112-118. (in Chinese)

[10]Zaǐtsev D I. Hypercyclic extensions of Abelian groups[J]. Mathematical Reviews, 1979: 16-37.

[11]Tate J. Nilpotent quotient group[J]. J. Topology, 1964, 3: 109-112.

[12]Gaschütz W. Zur erweiterungstheorie der endlichen gruppen[J]. Journal Für Die Reine Und Angewandte Mathematik, 1952, 190: 93-107.

[13]Gagola S, Isaacs I M. Transfer and Tate’s theorem[J]. Arch. Math., 2008, 91(4): 300-306.

[14]Roquette P. Über die existenz von hall-komplementen in endlichen gruppen[J]. J. Alg., 1964, 1: 342-346.

[15]Suzuki M. Group theory II[M]. New York: Springer-Verlag, 1986.

A Generalization of Huppert’s Splitting Theorem

JIA Ting-ting, HAO Cheng-gong

(School of Mathematical Sciences, Shanxi University, Taiyuan 030006, China)

The problem concerning when a finite group is splitting over a normal subgroup is studied and the famous Huppert’s splitting theorem ofp-version is generalized toπ-version. A detailed proof is supplied and a broader splitting criterion is obtained. The proof used the classical Gaschütz theorem and the transfer homomorphism. The main idea of the proof is from special to general. Finally, as applications of the theorem, unified and simplified proofs of some classical theorems in the theory of transfer are given.

splitting; normal subgroup; π-quotient; abelian π-quotient

1673-3193(2017)01-0027-04

2016-07-04

山西省自然科学基金资助项目(201601D011006)

贾婷婷(1990-)， 女， 硕士生， 主要从事群论的研究.

O152.1

A

10.3969/j.issn.1673-3193.2017.01.006