一类随机HIV病毒模型中正平衡点的稳定性研究*

李 洁， 董玲珍

(太原理工大学 数学学院， 山西 太原 030024)

一类随机HIV病毒模型中正平衡点的稳定性研究*

李 洁， 董玲珍

(太原理工大学 数学学院， 山西 太原 030024)

建立了一类带有随机扰动的随机HIV病毒模型. 通过研究该模型， 运用构造Lyapunov函数的方法， 分析了地方病平衡点的随机稳定性， 给出了地方病平衡点随机稳定的充分条件. 最后， 利用数值模拟的方法验证了所得结论.

随机因素； HIV模型； It公式；Lyapunov函数； 随机稳定性

0 引 言

近年来， 越来越多的传染病影响着人类的生产和生活. 众所周知， 艾滋病是严重危害人类健康的疾病之一. 艾滋病是由人类免疫缺陷病毒(HIV)引起的， HIV把人体中的T淋巴细胞作为攻击目标， 大量破坏并吞噬该细胞， 从而破坏人的免疫系统， 最终导致免疫力下降， 免疫系统崩溃， 使人类丧失对疾病的抵抗力， 最终引发死亡. 鉴于其对人类健康的严重威胁性， 近年来， HIV已经引起了国内外学者的广泛关注. 许多学者通过建立相应的HIV病毒传染的数学模型， 利用各种数学理论来研究模型的动力学行为， 进而为控制和治疗该疾病提供理论依据.

文献[1]中， 研究了一类HIV病毒模型的动力学行为， 讨论了平衡点的稳定性问题以及分支现象. 文献[2]中， 建立了一类带时滞的HIV-1模型， 研究了模型中平衡点的全局渐近行为. 同样， 在文献[3-4]中， 研究了各种HIV病毒模型， 并给出了病毒存在与绝灭的临界值-基本再生数. 文献[3]中建立了如下确定性HIV模型

(1)

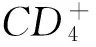
本文类似于文献[9]中添加白噪声干扰的方法， 对确定模型(1)添加相应的白噪声， 得到的随机模型为

(2)

式中：Bi(t)是标准的布朗运动；σi(i=1,2,3)为布朗运动的强度.

1 模型(2)的地方病平衡点的随机稳定性

显然， 当R0>1时， 系统(2)具有与系统(1)相同的地方病平衡点P*. 一个很自然的问题是: 系统中所引进的随机扰动如何影响系统的动力学行为. 特别是， 这一随机扰动是否会影响地方病平衡点的稳定性. 此即为本节将要讨论的主要内容. 首先介绍一些基本的定义与一些相关的引理.

在下文中， {Ω,F,{Ft}t≥0,P}是一个完备的概率空间， {Ft}t≥0满足一般的条件(它是线性增长和右连续的， 其中F0包括所有的P-null集).

考虑d维的随机微分方程如下[10]

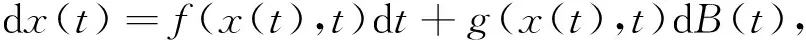
(3)

式中： B(t)是定义在上述概率空间上的标准布朗运动. 初值x(t0)=x0, x(t;t0,x0)表示t时刻随机微分方程(3)的平凡解或平衡位置.

定义 1[10]1) 若任意的ε∈(0,1)和r>0， 存在δ=δ(ε,r,t0)>0， |x0|<δ， 使得下面的条件满足

则系统(3)的平凡解是随机稳定的或者依概率稳定， 否则， 称随机不稳定.

2) 若平凡解是随机稳定的， 对于任意的ε∈(0,1)， 存在δ0=δ0(ε,t0)>0， |x0|<δ， 使得下面的条件满足

则称系统(3)的平凡解是随机渐近稳定的.

3) 若平凡解是随机渐近稳定的， 对于任意的x0∈ Rd， 使得下面的条件满足

则称系统(3)的平凡解是全局随机渐近稳定的.

引理 1[11]假设存在V函数: V(z,t)∈ C2(Ω)满足下面的条件

其中， ω>0， Ki(i=1,2,3)是正常数， 则对于t≥0， 系统(3)的平凡解是ω次指数稳定的， 当ω=2时， 平凡解是均方指数稳定的. 也就是说， 系统(2)的地方病平衡点是随机稳定的.

对于随机模型(2)有如下定理:

定理 1 若R0>1， 且满足

那么该系统的地方病平衡点P*是随机稳定的. 其中R0仍为文献[1]中所定义的基本再生数.

证明 对模型(2)作变换， 令X=x-x*， Y=y-y*， Z=v-v*， 可得到

(kY+ky*-uZ-uv*)dt+σ3ZdB3(t)=

(kY-uZ)dt+σ3ZdB3(t).

不妨仍用x， y， z 分别表示X， Y， Z， 那么可以得到如下模型

(4)

其中， a>0， b>0， c>0待定. 令

由It公式， 可得

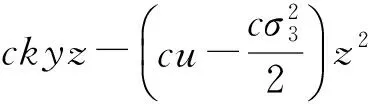
从而

LV1+LV2+LV3=

选取a(d+p)=bβv*， 则有

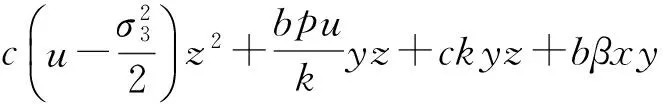
又因

故

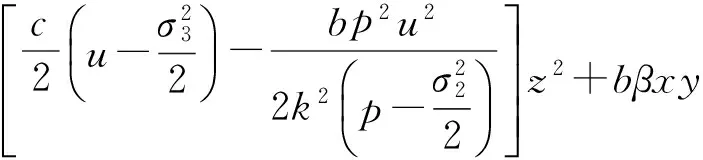
由已知， 得

又由于

从而

可以选取合适的a>0， c>0， 使之满足:

即

(5)

且

(6)

由式(5)和式(6)， 可以得到

(7)

(8)

(9)

(10)

即

又因bβxyz=o(x2+y2+z2)， 故

LV=LV1+LV2+LV3=

其中

这样，由引理1知，模型(4)的零解是随机稳定的，即随机模型(2)的地方病平衡点是随机稳定的.

2 数值模拟

本文采用文献[12]中的离散方法对模型(2)进行离散， 从而对确定性模型和相应的随机模型进行数值模拟， 分析随机扰动对系统正平衡点稳定性的影响.

选取初值x1=50， y1=50， v1=5， 选取参数λ=10， β=0.01， d=0.1， k=0.1， p=0.1， u=0.8， 易求得R0=1.25>1， 此时确定性系统(1)存在全局稳定的正平衡点(80,20,2.5). 在该系统中引进随机扰动:

1) 取白噪声强度系数为σ1=σ2=σ3=0.05， 利用Matlab软件， 可以分别得到随机模型和确定模型中x(t)， y(t)， v(t)随时间t变化的对比图像， 如图 1 所示.

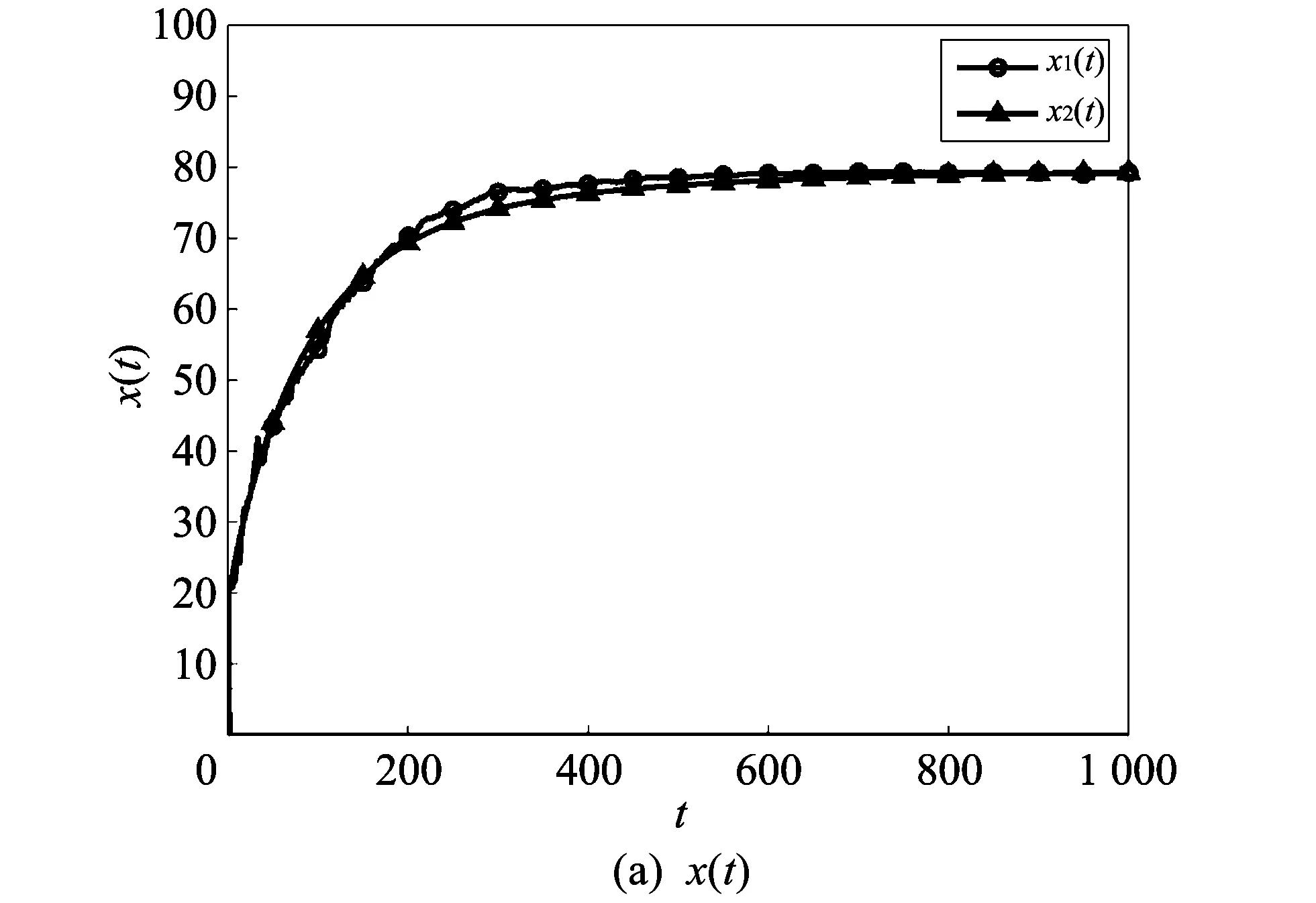
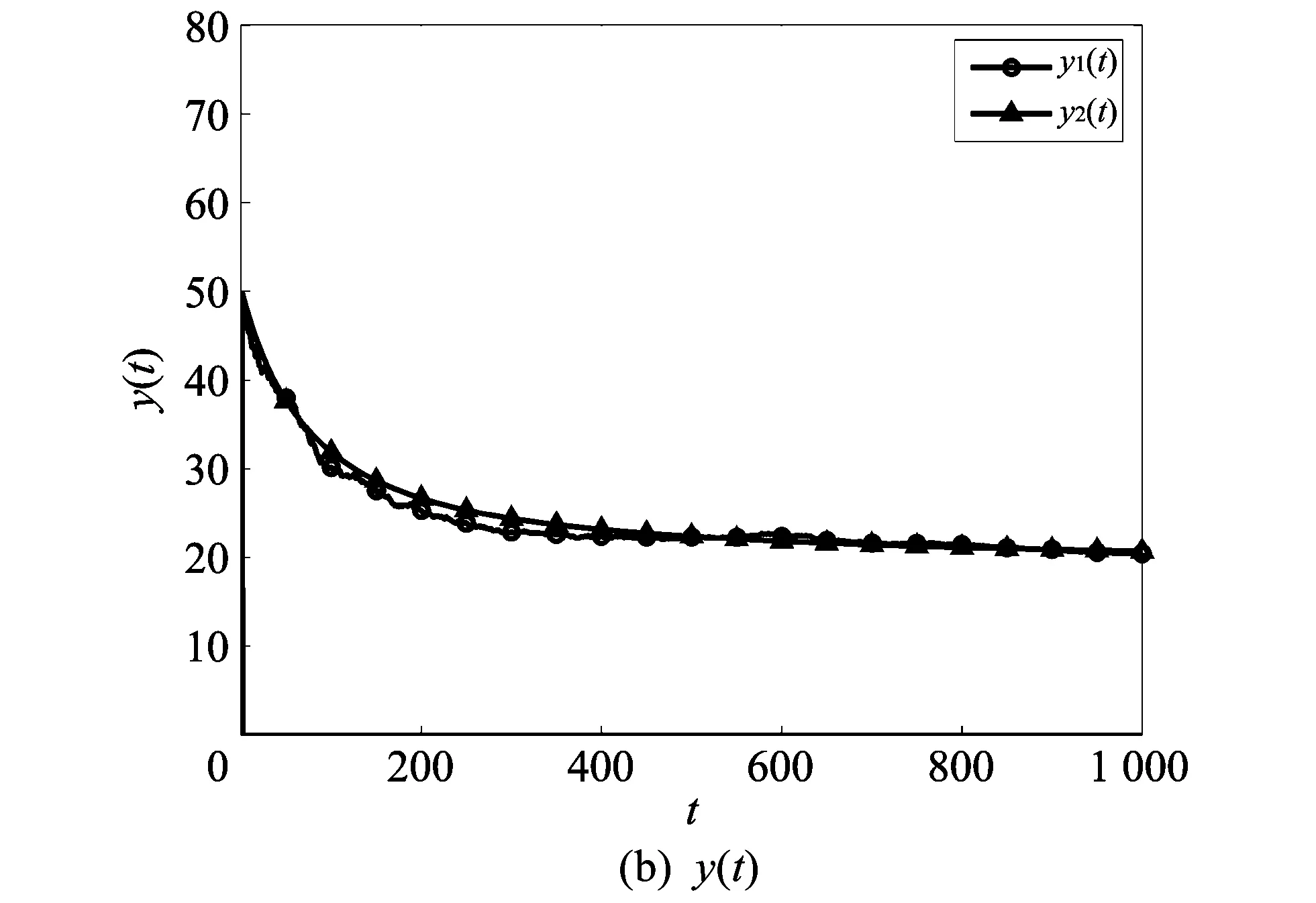
图 1 σ1=σ2=σ3=0.05时系统(2)与系统(1)中 x(t)，y(t)，v(t)随时间t的变化对比图Fig.1 Change of x(t), y(t) and v(t) with time in σ1=σ2=σ3=0.05

2) 取白噪声强度系数为σ1=σ2=σ3=0.1， 利用Matlab软件， 可以分别得到随机模型和确定模型中x(t)， y(t)， v(t)随时间t变化的对比图像， 如图 2 所示.

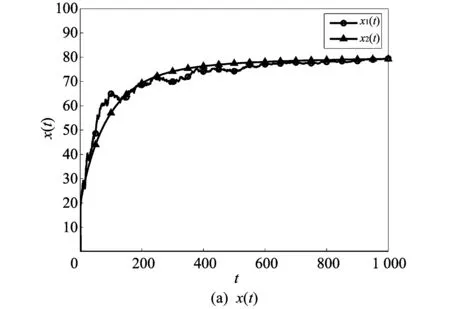
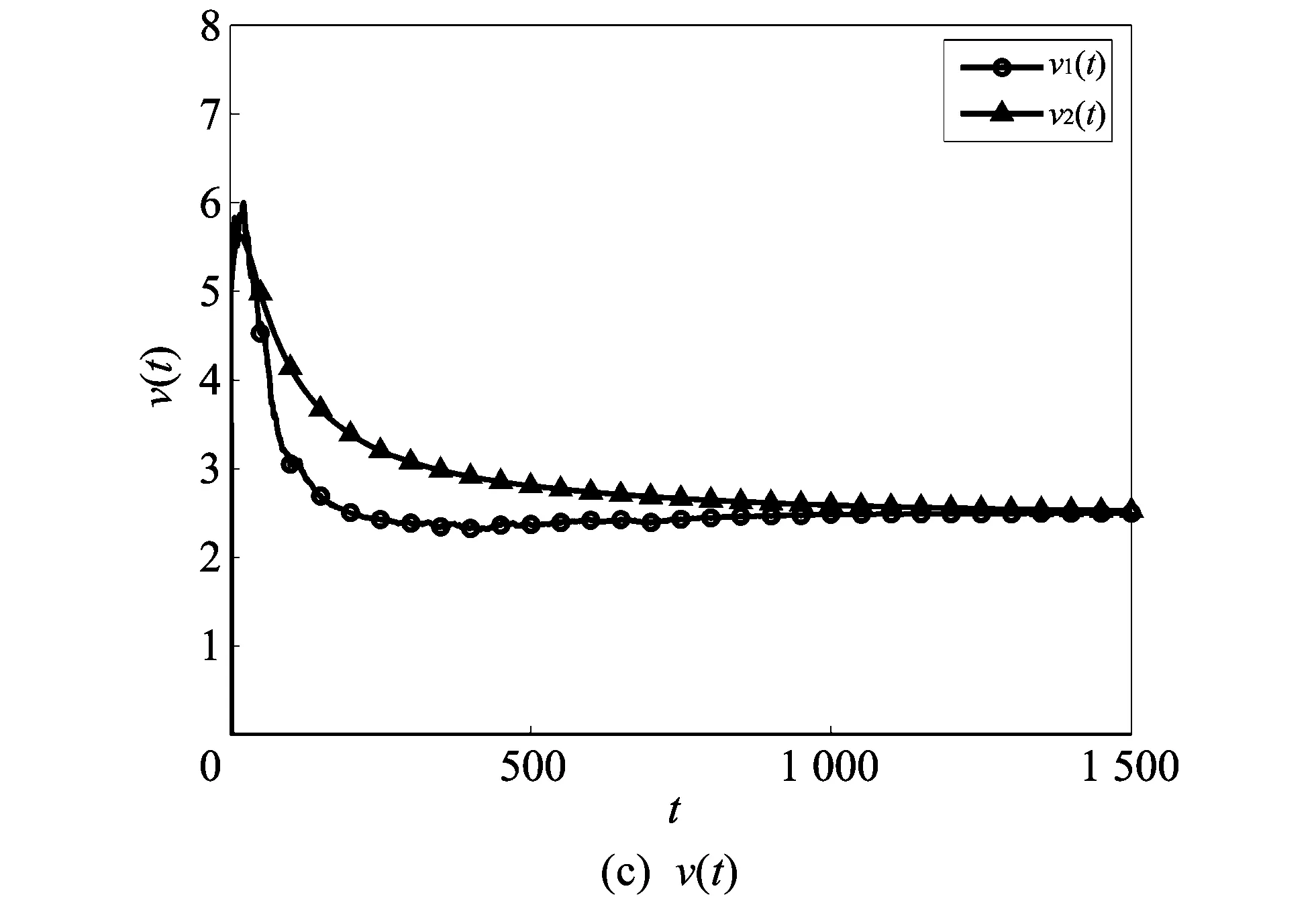
图 2 σ1=σ2=σ3=0.1时系统(2)与系统(1)中 x(t)，y(t)，v(t)随时间t的变化对比图Fig.2 Change of x(t), y(t) and v(t) with time in σ1=σ2=σ3=0.1

图 1 和图 2 的标注中， x1(t)，y1(t)，v1(t)分别表示随机模型中健康T细胞， 被感染T细胞和HIV病毒粒子的浓度随时间t的变化图像； x2(t)， y2(t)， v2(t)分别表示确定模型中健康T细胞， 被感染T细胞和HIV病毒粒子的浓度随时间t的变化图像. 图 1 和图 2 表明：1) 确定模型(1)的正平衡点是渐近稳定的， 随机模型(2)的解在确定模型(1)的解附近做随机振动， 且当t→+∞时， 随机系统(2)的解趋于正平衡点；

2) 在满足定理1的条件下的白噪声强度中， 噪声强度越小， 解的振动幅度越小； 相反， 噪声强度越大， 解的振动幅度越大. 说明噪声强度的大小影响着随机系统解的振动幅度.

[1]Luo J， Wang W， Chen H， et al. Bifurcations of a mathematical model for HIV dynamics[J]. J. Math. Anal. Appl.， 2016, 434(1)： 837-857.

[2] Li D， Ma W. Asymptotic properties of an HIV-1 infection model with time delay[J]. J. Math. Appl.， 2007, 335(1)： 683-691.

[3]Nowak M， Bangham C. Population dynamics of immune responses to persistent virus[J]. Science， 1996, 272(5258)： 74-79.

[4]Huang G， Ma W， Takeuchi Y. Glabal properties for virus dynamics model with Beddington-DeAngelis functional response[J]. Appl. Math. Lett.， 2009， 22(11)： 1690-1693.

[5]Dalal N， Greenhalgh D， Mao X. A stochastic model for internal HIV dynamics[J]. J. Math. Anal. Appl.， 2008, 341(2)： 1084-1101.

[6] Carvalho A R M， Pinto C M A. The effect of noise intensity in a stochastic model for HIV-specific helper cells[J]. IFAC-PapersOnLine， 2015, 48(1)： 186-187.

[7]Dalal N， Greenhalgh D， Mao X. A stochastic model of AIDS and condom use[J]. J. Math. Anal. Appl.， 2007, 325(1)： 36-53.

[8]Tuckwell H， Corfec E L. A stochastic model for early HIV-1 population dynamics[J]. J. Theoret. Biol.， 1998, 195(4)： 451-463.

[9]Yu J， Jiang D， Shi N. Global stability of two-group SIR model with random perturbation[J]. J. Math. Appl.， 2009, 360(1)： 235-244.

[10] Mao X. Stochastic Differential Equations and Applications[M]. Chichester： Horwood Press， 1997.

[11] Arnold L. Stochastic Differential Equations: Theory and Applications[M]. New York： Wiley Press， 1974.

[12] 冯晓龙. 基于MATLAB随机种群模型数值模拟方法的应用研究[J]. 计算机应用与软件， 2014, 31(9)： 81-82. Feng Xiaolong. On application of numericial simulation approach for stochastic population model based on Matlab[J]. Computer Applications and Software， 2014, 31(9)： 81-82. (in Chinese)

Stability of the Endemic Equilibrium in a HIV Model with Random Perturbation

LI Jie， DONG Ling-zhen

(College of Mathematics， Taiyuan University of Technology， Taiyuan 030024， China)

A class of HIV model with random perturbation is established, and by using Lyapunov function, the stochastic stability of endemic equilibrium is analyzed, then the sufficient condition of the stochastic stability of endemic equilibrium is given. Finally, numerical simulations are carried out to support the theoretical analysis.

random perturbation； HIV model； Itformula； Lyapunov function； stochastic stability

1673-3193(2017)01-0019-05

2016-03-04

教育部科学技术研究重点项目(210030)； 山西省自然科学基金资助项目(2013011002-3)

李 洁(1990-)， 女， 硕士生， 主要从事微分方程理论及其应用研究.

O175

A

10.3969/j.issn.1673-3193.2017.01.004