有界噪声激励下神经系统中反随机共振现象研究*
王 甲, 李东喜
(太原理工大学 数学学院, 山西 太原 030024)
有界噪声激励下神经系统中反随机共振现象研究*
王 甲, 李东喜
(太原理工大学 数学学院, 山西 太原 030024)
为了考察噪声对神经元系统中内部信息传递的作用, 研究了有界噪声对神经元放电行为的影响, 特别是噪声对神经元放电的抑制效应即反随机共振现象. 通过蒙特卡洛随机模拟方法, 系统研究了当输入电流激发神经元持续放电的情况下, 有界噪声中各参数对神经元平均放电率的影响. 研究发现, 随机相位能抑制神经元的放电行为, 即产生反随机共振现象; 振幅越大, 频率越小, 抑制效果越明显; 且在稳定的振幅和频率条件下, 电流强度越小, 平均放电率越小, 抑制效果越明显. 该抑制效应的研究对生物医学疾病如癫痫具有重要的理论意义.
有界噪声; Hodgkin-Huxley神经元模型; 抑制效应; 反随机共振
神经系统中噪声能潜在地提高系统的信息处理能力这一特性使得噪声对神经元放电的影响得到越来越多的关注, 并发现了随机共振的机制, 即微弱的输入信息可以被放大, 并在噪声的激励下得到优化. 之前的实验和理论研究表明, 噪声可以改善检测、 集成和传输的信号, 并且导致许多复杂的特征, 比如同步性和放电性[1-2]. 与随机共振相比, 最近的研究大都集中在随着噪声强度的增大产生在节奏放电过程中的抑制效果, 特别是小幅度的噪声可降低平均放电率, 甚至完全停止神经元的放电活动. 由于此噪声神经元反应的机理与随机共振是相反的,故称这种新现象为反随机共振现象. 在大脑中, 神经元放电活动涉及极限环在正常和癫痫状态下的活性, 如果这种振荡附近出现一个分岔点, 那么靠近分叉点噪声就可以很容易地使细胞进入静息状态, 随着噪声水平的继续增强细胞将再次回到正常放电状态, 这便是一个由噪音引起的反随机共振现象[3-7]. 实际上, 反随机共振机制广泛存在于各种生物医学和金融经济现象中, 如何利用其机制趋利避害是目前许多交叉学科的研究热点.
反随机共振的研究始于噪声在乌贼轴突效应下对体外的神经起搏器的影响, 从中发现小噪声可以诱发重复放电和静息之间的切换行为, 这意味着当输入电流强度达到放电阈值时, 在一个适度的噪声强度范围内存在一个最小的甚至静息的放电状态[8]. 最近有学者研究了Hodgkin-Huxley神经元模型(简称HH模型)中加性高斯白噪声和传导噪声对神经元重复放电的影响[3], 在加性高斯白噪声激励下, 当平均输入电流密度在6.6 μA/cm2这一放电阈值附近时, 随着噪声水平的增大, 150 ms 内放电产生的尖峰数目出现了明显的最小值[4]; 在传导噪声驱动下, 当电导系数不是远远高于0.112 mS/cm2这一放电阈值时, 随着噪声水平的增加平均放电率也出现了明显的最低值[5]. 郭大庆研究了HH模型在高斯色噪声激励下的神经元放电现象时也得到了类似的结论, 并发现高斯色噪声对神经元放电的抑制效果要比高斯白噪声强[6]. Muhammet Uzuntarla另辟蹊径, 在Morris-Lecar(ML)神经元模型中通过改变突触电流也发现了神经元放电的抑制效果[7], 使得反随机共振研究得到进一步拓展.
由于白噪声在现实世界中不存在, 且又是无界的, 故假设随机因素为白噪声情形有其一定的缺陷和局限性. 本文假设随机因素为一种有界噪声, 相对于白噪声而言, 有界噪声既考虑了噪声振幅和频率, 又考虑了随机相位, 更符合噪声的实际形态. 为此, 本文研究了有界噪声对神经元放电的抑制效应即反随机共振现象. 通过引入平均放电率, 系统研究了输入电流和有界噪声共同作用对神经元放电行为的影响.
1 模型和噪声
1.1 Hodgkin-Huxley神经元模型
1952 年, Hodgkin和Huxley利用电压钳在实验室中发现了鱿鱼(乌贼)巨轴突上的细胞膜与形成动作电位的离子电导的时间特征, 同时测定出电流与电压的关系, 建立了一套神经元模型, 即Hodgkin-Huxley神经元模型[9], 其精确描述了动作电位的生理特征, 如动作电位沿轴突的传播、 兴奋性、 适应性等[10]. HH神经元模型由4个非线性微分方程组成, 表示为
(1)

方程组中n表示某种粒子处于正确位置时才能打开钾例子通道的概率;αn为钾离子通道从关闭状态到开启状态的速度常数;βn为钾离子通道从开启状态到关闭状态的速度常数;m为钠离子通道活化过程参数, 表示某一特性粒子处于正确位置时钠离子通道激活过程中的概率;h为钠通道失活化过程参数, 表示某一特性粒子处于正确位置时钠离子通道失活过程中的概率;αm,βm,αh和βh均为描述钠离子通道状态变化的. 为了研究噪声对HH模型中神经元放电的影响, 采用最常用的Fox算法[11], 控制变量αn,βn,αm,βm,αh和βh遵循以下方程
(2)
1.2 有界噪声
高斯白噪声, 高斯色噪声以及非高斯色噪声等噪声都是无界的, 噪声路径并没有一个严格的范围. 本文采用有界噪声, 其形式为[12]

(3)

式中:A和ω分别是表示有界噪声的振幅以及频率;W(t)是标准维纳过程;γ是添加到维纳过程W(t)上的噪声强度. 有界噪声ξ(t)可以改写成如下微分形式
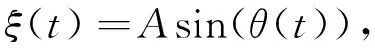

(4)

或者可以将其理解成如下的积分形式
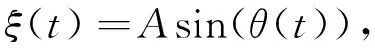
(5)
式中:ζ(t)是高斯白噪声.
由方程(5)以及高斯白噪声的性质可以知道,θ(t)的均值〈θ(t)〉=ωt, 自相关函数〈θ(t)θ(t+τ)〉=ω2t(t+τ)+γ2min(t,t+τ),τ>0. 这说明ξ(t) 的均值和自相关函数如下

(6)
当t→∞时,ξ(t)的均值和自相关函数变为


(7)
在极限条件下, 功率谱密度为
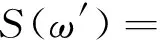
(8)
2 有界噪声激励下反随机共振现象
在生物细胞中, 神经元的放电现象被认为是一个由于存在多种噪声来源引起的随机过程. 随机性显然是通过产生高度变量脉冲序列的神经元来体现的, 并在神经元周围环境的各种刺激下自发地进行神经活动.
在非线性动力系统中, 神经元在同一频率能够节奏性放电[14], 这样产生的稳定极限环经常出现一个分岔机理[15], 当一个参数, 如电流强度在HH模型中不断变化时, 可能会产生某一临界阈值. 从图1电流阈值图中发现,HH模型中引起神经元产生尖峰放电的电流临界阈值为μ=4.156 6mA, 即电流强度达到μ=4.156 6mA时神经元才能由稳定的静息状态进入放电状态: 低于临界值时, 神经元基本处于静息态, 不能产生稳定的极限环, 膜电位稳定在0mV左右, 如图 1 相图中无噪声且电流强度μ=4mA时; 高于临界值时, 神经元会放电并产生尖峰, 形成一个稳定的极限环, 如图 2 相图中无噪声且电流强度μ=6.6mA时. 一旦有噪声干扰, 极限环的吸引域就会变得比较狭窄, 如图2有噪声的情况时, 一定强度的噪声甚至可以让神经元达到静止状态, 使放电行为终止: 当噪声小时, 通常静息态会维持很长的时间, 但对于较大的噪声, 放电行为恢复并随后出现一段静息状态.
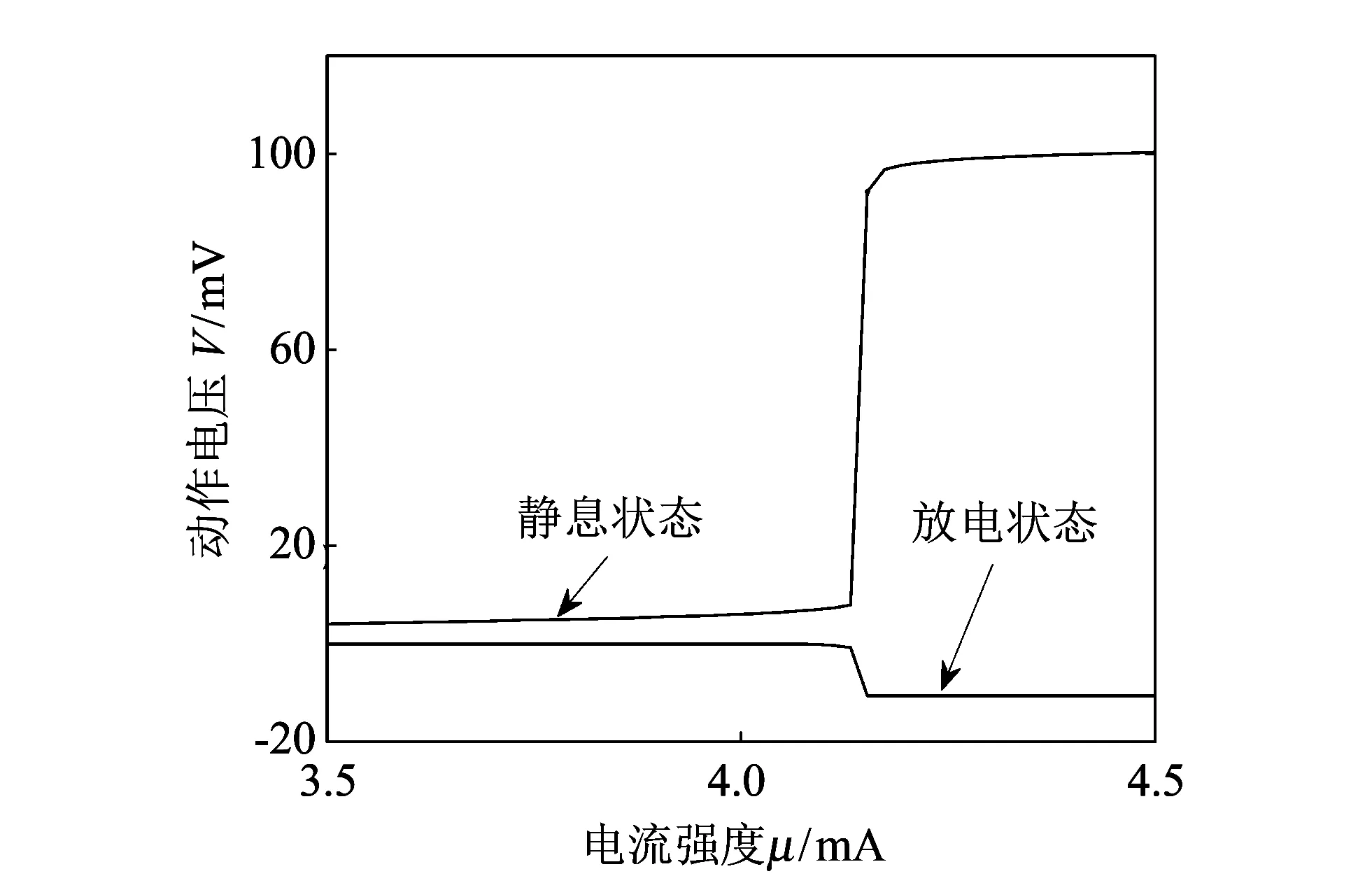
图 1 电流阈值图Fig.1 Figure of current threshold
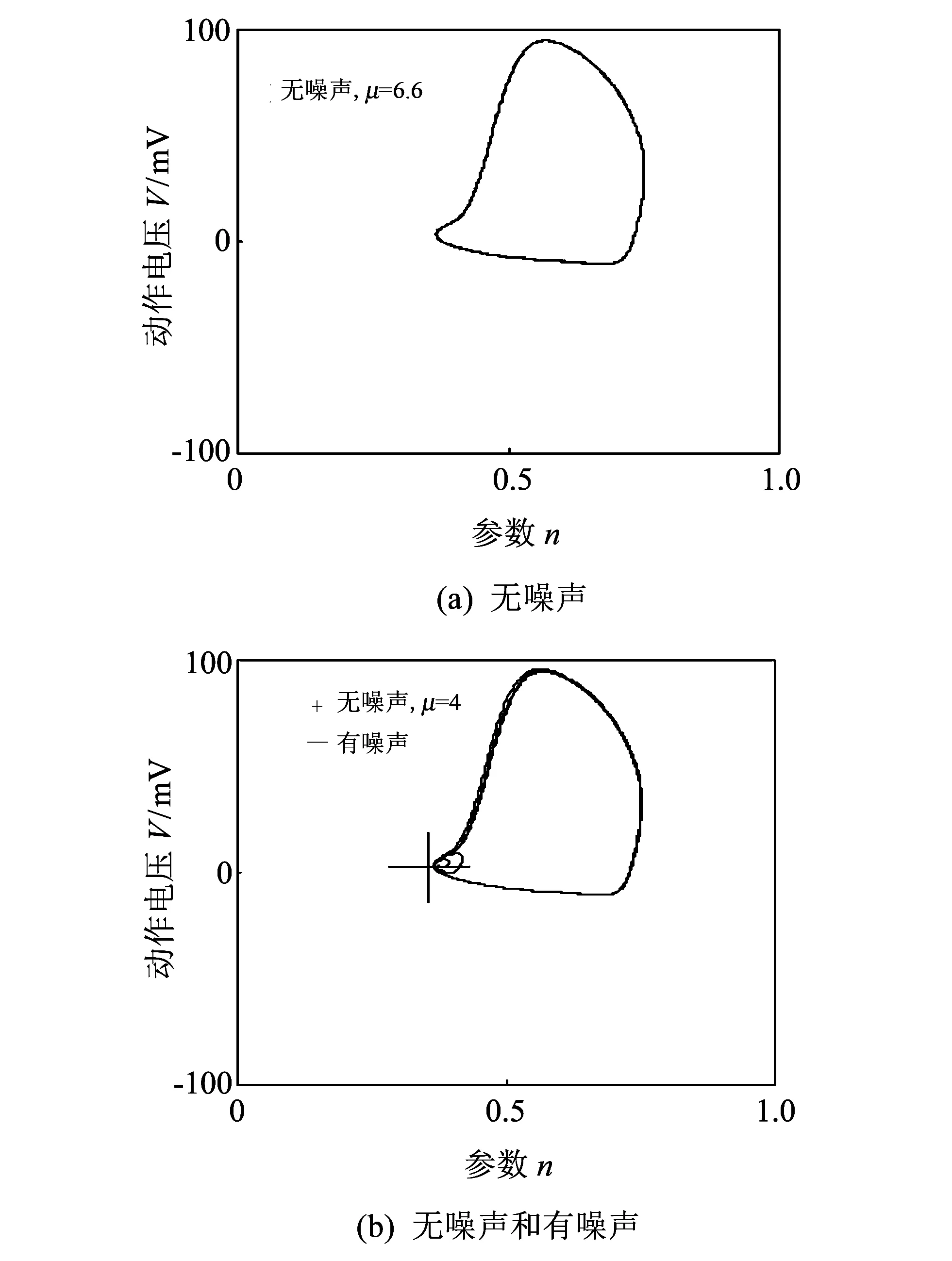
图 2 相图Fig.2 Phase diagram
计算模型的平均放电率以求得等概率随机均匀选择的固定在四维状态空间(V,m,n,h)的区域A神经元的膜面积固定值率, 并输入电流I0. 然后计算发生时间间隔τ的尖峰的数目. 每个尖峰事件限定向上交叉的膜电位阈值为50 mV. 这整个过程被重复N次, 平均放电速率[16]
(9)
利用数值模拟方法, 固定频率ω=0.5 Hz, 电流μ=6.6 mA, 得到图 3(a), 研究振幅不同的情况下神经元平均放电率关于噪声强度的变化情况. 可以看出, 达到神经元放电的电流阈值后, 随着噪声强度的增大, 神经元平均放电率都呈现出先减小后增大的趋势, 即出现了反随机共振现象. 当噪声强度不足以抑制尖峰放电时(小于101量级), 平均放电率随着噪声强度的增大呈现快速递减的趋势, 当不再受到抑制时(大于101量级), 平均放电率随噪声强度增大单调递增. 因此神经元放电受有界噪声振幅的影响, 在一定范围内, 振幅越大, 抑制效果越明显. 有界噪声的振幅A在一定条件下能抑制神经元放电, 这与以往白噪声强度在一定条件下能抑制神经元放电具有类似的结论[5].


图 3 有界噪声激励下振幅A, 频率ω和电流μ变化 对平均放电率的影响Fig.3 Influence of amplitude, frequency and current intensity on average spiking rate driven by bounded noise
其次, 固定振幅A=2, 电流μ=6.6 mA得到图 3(b), 研究频率不同的情况下神经元平均放电率关于噪声噪声强度的变化情况. 可以看到, 振幅ω取不同值时随着噪声强度的增大, 均出现了神经元放电的抑制效果, 并且随着频率的增加, 神经元出现最弱的放电现象时所对应的噪声强度越来越大, 不再有抑制效果时, 原来抑制效应最好的恢复到促进状态时的效果最佳. 可以总结出神经元平均放电率受到有界噪声频率ω的影响, 在抑制效果值域范围内, 频率越小, 反随机共振效果越佳, 恢复到促进放电状态时反倒是频率越大, 促进效果越佳. 此外, 与以往研究高斯白噪声[3-5]和色噪声[6]相比, 有界噪声可以明确地研究噪声的频率对神经元放电行为的影响, 而不仅仅考虑噪声强度和相关时间等随机因素对其影响.
最后, 固定振幅A=0.5, 频率ω=7 Hz, 得到图 3(c), 研究电流强度对神经元平均放电率的影响. 能够发现, 当电流强度达到放电阈值以后, 神经元平均放电率随着噪声强度的增大呈现先减小后增大的情况, 抑制效果很好, 并且平均放电率对电流强度敏感度很高, 电流强度很小的变化足以引起放电抑制效果的很大差异, 从而得出达到放电阈值后的电流强度的大小对神经元放电抑制效果敏感性很大, 在适当的范围内, 电流值越小放电抑制效果越好.
3 结 论
本文系统研究了有界噪声对神经元放电行为的影响, 结果显示噪声能使神经元原来的放电行为受到抑制. 同时研究发现, 随机相位能抑制神经元的放电行为, 即产生反随机共振现象; 振幅越大, 频率越小, 抑制效果越明显; 且在稳定的振幅和频率条件下, 电流强度越小, 平均放电率越小, 抑制效果越明显.
此外, 由于随机噪声的存在使得神经元放电行为受到抑制的现象出现在多种神经元模型中, 由此可以断言反随机共振现象在神经及生物系统中是普遍存在的. 此外, 由于时滞的普遍存在性, 时滞系统中噪声的抑制效应亦值得关注. 为此, 研究多种神经及生物系统、 时滞系统中反随机共振现象是下一步需研究的课题, 尤其是在常见生物医学疾病比如情感性精神障碍的应用研究亦有待进一步挖掘.
[1]Goychuk I, Hanggi P. Non-stationary stochastic resonance viewed through the lens of information theory[J]. Eur.Phys. J. B, 2009, 69: 29-35.
[2]Lee S G, Kim S. Excitable membranes: channel noise, synchronization and stochastic resonance[J]. Phys. Rev. E, 2002, 42: 359-370.
[3]Tuckwell H C, Jost J. Analysis of inverse stochastic resonance and the long-term firing of Hodgkin-Huxley neurons with Gaussian white noise[J]. Physica A, 2012, 391: 5311-5325.
[4]Tuckwell H C, Jost J. Weak noise powerfully inhibits rhythmic spiking but not its propagation[J]. PLoS Comput. Biol, 2010, 6(5): e1000794.
[5]Gutkin B S, Tuckwell H C, Jost J. Inhibition of rhythmic neural spiking by noise: the occurrence of a minimum in activity with increasing noise[J]. Naturwissenschaften, 2009, 96: 1091-1097.
[6]Guo Daqing. Inhibition of rhythmic spiking by colored noise in neural sysytems[J]. Cogn Neurodyn, 2011, 5: 293-300.
[7]Uzuntarla M. Inverse stochastic resonance induced by synaptic background activity with unreliable synapses[J]. Physics Letters A, 2013, 377: 2585-2589.
[8]Paydarfar D, Forger D B, Clay J R. Noisy inputs and the induction of on-off switching behavior in a neuronal pacemaker[J]. Neurophysiology, 2007, 96(6): 3338-3348.
[9]Tuckwell H C. Spike trains in a stochastic Hodgkin-Huxley system[J]. Biosystems, 2005, 80(1): 25-36.
[10]Hodgkin A L, Huxley A F. A quantitative description of membrane current and its application to conduction and excitation in nerve[J]. Physiol, 1952, 117(4): 500-544.
[11]Fox R F. Stochastic versions of the Hodgkin-Huxley equations[J]. Biophys J, 1997, 72: 2068-2074.
[12]Li Dongxi, Xu Wei, Yue Xiaole, et al. Bounded noise enhanced stability and resonant activation[J]. Nonlinear Dynamics, 2012, 70(3): 2237-2245.
[13]Stratonovich R L. Topics in the theory of Random noise[M]. New York: Gorden and Breach, 1963.
[14]Glass L. Synchronization and rhythmic processes in physiology[J]. Nature, 2001, 410: 277-284.
[15]Wang Huaxia, Wang Qingyun, Lu Qishao. Bursting oscillations, bifurcation and synchronization in neuronal systems[J]. Chaos, 2011, 44(8): 667-675.
[16]Uzuntarla M, Cressman J R, Ozer M E, et al. Dynamical structure underlying inverse stochastic resonance and its implication[J]. Phys. Rev. E, 2013, 88: 042712-6.
Inverse Stochastic Resonance in Neural System Induced by Bounded Noise
WANG Jia, LI Dong-xi
(College of Mathematics, Taiyuan University of Technology, Taiyuan 030024, China)
In order to study the effect of noise on the information transmission in neural system, firing of neural system driven by the bounded noise was discussed, especially the inhibitory effect of neuron firing, which was called the phenomenon of inverse stochastic resonance. Through the stochastic simulation method of Monte Carlo, the influence of parameters of bounded noise on the average spiking rate was systemic studied when the neurons were in the continuous firing state under the input current. Investigation results indicate that random phase can restrain neural spiking and induce the phenomenon of inverse stochastic resonance. Meantime, the bigger the amplitude is, and the smaller the frequency is, the better of the inhibition on the neural spiking is. In addition, the smaller the current intensity is, the smaller the average spiking rate is and it is means that the inhibition effect is more distinct. The research of inhibitory effect gives an important theoretical significance on the treatment of medical diseases such as epilepsy.
bounded noise; Hodgkin-Huxley neuron model; inhibitory effect; inverse stochastic resonance
1673-3193(2017)01-0031-05
2016-03-24
国家自然科学基金资助项目(11402157); 山西省回国留学人员科研资助项目(2015-032)
王 甲(1991-), 女, 硕士生, 主要从事生物系统动力学的研究.
O211.6
A
10.3969/j.issn.1673-3193.2017.01.007

