有限挠度Bernoulli-Euler梁中的非线性波与混沌行为*

周义清， 张 伟， 张善元

(1. 北京工业大学 机电学院， 北京 100124； 2. 北京城市学院， 北京 100083；3. 太原理工大学 应用力学与生物医学工程研究所， 山西 太原 030024)

有限挠度Bernoulli-Euler梁中的非线性波与混沌行为*

周义清1,2， 张 伟1， 张善元3

(1. 北京工业大学 机电学院， 北京 100124； 2. 北京城市学院， 北京 100083；3. 太原理工大学 应用力学与生物医学工程研究所， 山西 太原 030024)

基于有限挠度理论， 导出了Bernoulli-Euler梁的非线性偏微分方程形式的弯曲波动方程， 利用行波解法和积分技巧， 将非线性偏微分方程转化为常微方程. 定性分析表明， 在一定条件下， 动力系统有异宿轨道， 对应冲击波解. 利用Jacobi椭圆函数法， 得到了波动方程的准确周期波解， 当Jacobi函数的模数m→1时， 得到系统的冲击波解. 显然， 阻尼和外载荷的摄动将使异宿轨道破裂， 得到横截异宿点. 通过Melnikov函数法得到了系统出现横截异宿点的阈值条件， 这表明， 系统存在Smale马蹄意义下的混沌行为.

Bernoulli-Euler梁； 有限变形； 非线性波； 混沌； Melnikov函数

梁是工程中无处不见的结构， 在各个领域都有其广泛和重要的作用. 非线性波动理论已成功应用于气象学、 光线通信、 激光打靶密度坑问题和地下油气藏的勘探等领域. 研究梁中非线性波动问题， 对固体结构中的波动应用具有探索性的意义. 非线性波动和混沌都会涉及到同(异)宿轨道的问题[1-3]， 已有学者通过对非线性波动方程的摄动， 讨论过非线性波的混沌运动[4-5]. 一个真实的梁结构中， 阻尼耗散和外载荷的激励总是不可避免的. 课题组之前已使用Hamilton原理建立了大挠度梁的非线性支配方程， 并对阻尼和外载荷摄动后的混沌现象进行了理论研究. 本文将按照上述思路， 基于文献[6-8]， 研究Bernoulli-Euler梁结构中非线性波动和非线性混沌行为.

1 支配方程的导出

考虑一个均匀无限长梁， 横截面积为A， 弹性模量为E， 转动惯量为I， 密度为ρ, 如图 1 所示. 梁承受横向分布荷载， 载荷密度为q(x,t). 梁未受扰动前， 中面任意点P的轴向和横向位移分别为u(x,t)和w(x,t). 图 2 描述的是梁微单元dx在现时构形下任意时刻t的位移和受力状态.

图 1 梁单元的初始构形Fig.1 Initial configuration of microelement

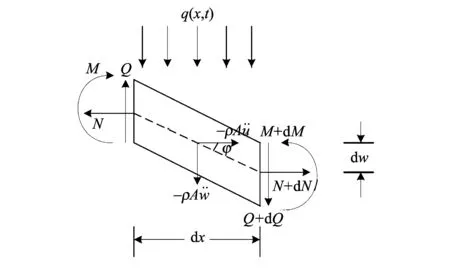
图 2 现时构形梁单元受力分析Fig.2 Force analysis of microelement in current configuration

以梁微元体为研究对象， 依据动力学平衡条件， 可得如下方程组

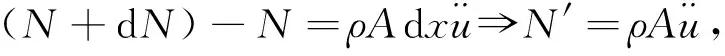
(1)

(2)

(M+dM)-M-Q(dx+du)+Ndw=

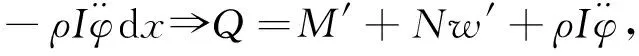
(3)

式中：M,Q,N分别为梁截面上的弯矩、 剪力和轴力；x和t分别表示轴向坐标和时间. 式中， “′”和 “·”分别表示对x和t求偏导.

梁的中面伸长应变-位移关系为

(4)

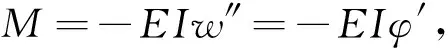
(5)

(6)

式中：φ=w′；E为弹性模量. 将本构关系(5)， (6)和几何方程(4)代入到平衡方程(1)， (2)和(3)中， 对x求一次偏导， 可得支配Bernoulli-Euler弯曲波传播的非线性偏微分方程组

(7)

(8)

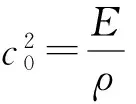
2 行波解法及方程的简化

假定u=u(ξ)， φ=φ(ξ)， q=q(ξ), ξ=k(x-ct). 此处k是与波宽有关的参数， c为波速， 上述式子存在以下运算关系

(9)

用行波法求解方程(7)和(8)， 可得忽略阻尼和外载荷之后的系统支配方程为

(10)

其中

(11)

3 支配方程的定性分析及求解

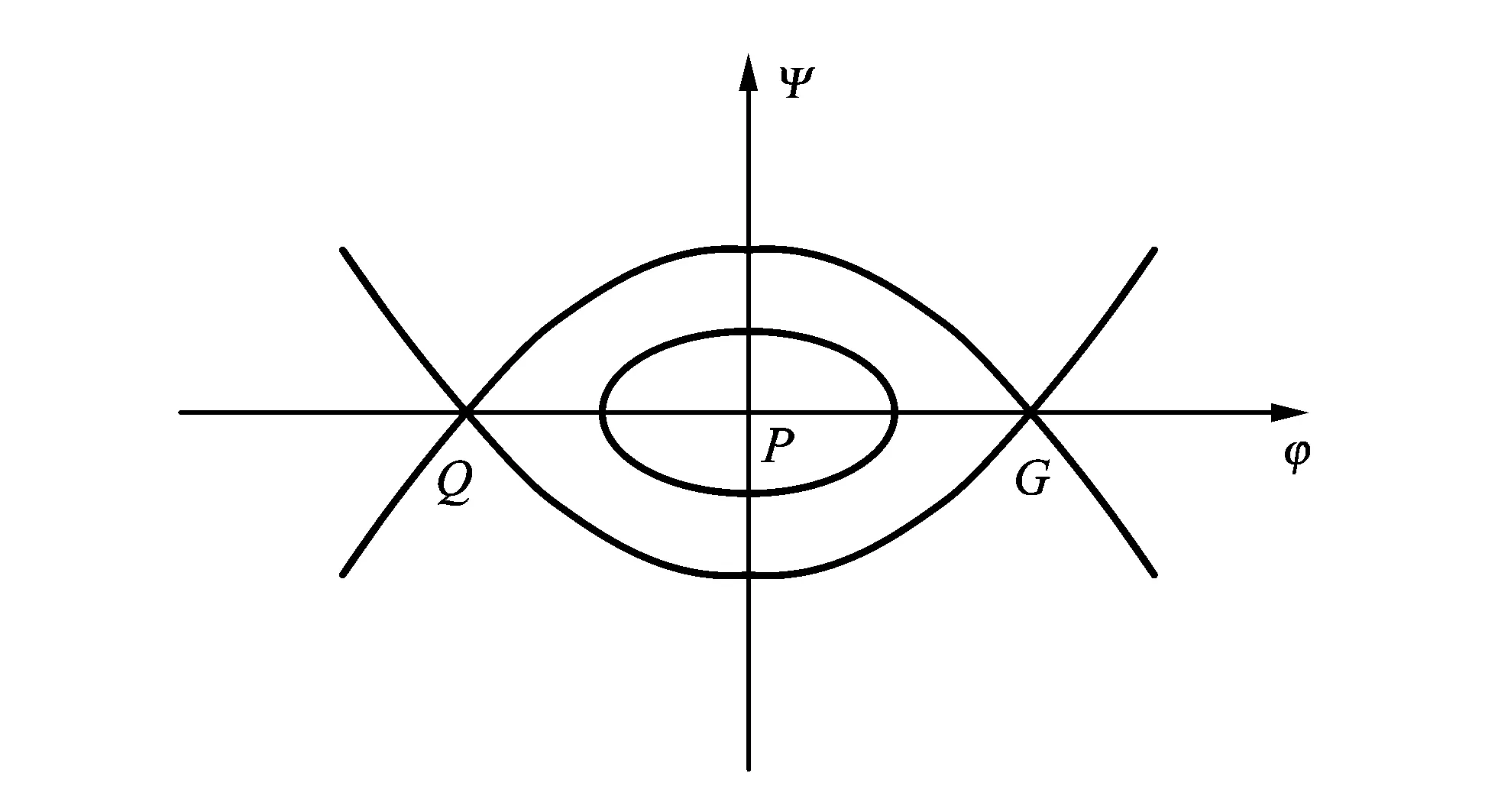
图 3 当c>c0时异宿轨道相图Fig.3 Heteroclinic orbit phase diagram when c>c0

利用Jacobi椭圆正弦函数展开法求解方程(10)， 得到有限挠度Bernoulli-Euler梁方程的精确周期波解为

(12)

当m→0时， snξ→sinξ， 得线性波解

(13)

当m→1时， 得冲击波解

(14)

或

(15)

其中

(16)

4 阻尼和外载荷对系统的摄动[9-10]

一个真实的动力系统， 总是存在阻尼和外载荷， 所以， 考虑系统的阻尼和外载荷后可得系统的动力学支配方程为

(17)

由Melnikov函数可以得到出现Smale马蹄意义下混沌的充要条件， 混沌阈值曲线如图 4 所示， 此处略去推演过程， 直接给出条件如下

(18)

其中

(19)

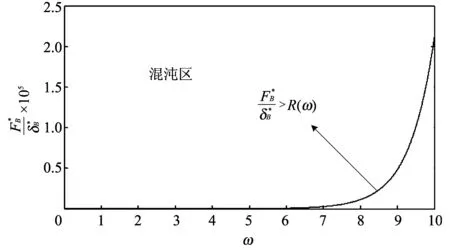
图 4 混沌阈值曲线Fig.4 Chaotic region

5 数值模拟

图 5 方程(17)的相图Fig.5 The phase diagram of equation (17)

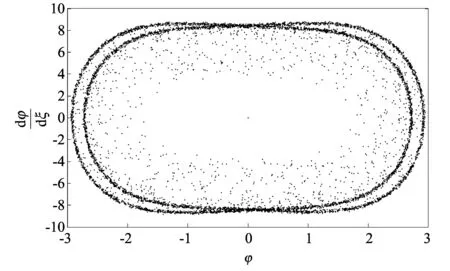
图 6 poincaré映射Fig 6 The poincaré map

6 结果与讨论

本文研究了无限长Bernoulli-Euler梁中非线性弯曲波的传播. 定性分析表明， 系统存在异宿轨道， 利用Jacobi椭圆函数展开法得到了系统的精确周期解， 当模数m→1时， 系统存在冲击波解. 考虑系统阻尼和外加载荷的情况下， 对非线性波动方程进行了摄动. 利用Melnikov函数给出了系统混沌运动的条件， 在给定参数下， 进一步用数值软件进行了模拟， 模拟结果表明， 系统出现了Smale马蹄意义下的混沌.

通过研究梁中的非线性波， 可以反映其非线性动力学行为， 分析其非线性波动产生机理以及各参数对非线性波动的影响， 可以将研究成果应用于提高构件性能和服役寿命. 了解和掌握梁中的混沌动力学特性， 通过改变系统产生混沌运动的条件， 达到消除或抑制振动的目的， 以此用来解决实际工程问题.

[1]Thompson J M T, Virgin L N. Spatial chaos and localization phenomena in nonlinear elasticity[J]. Physics Letters A, 1988, 126(8/9)： 491-496.

[2]Cross M C, Hohenberg P C. Spatiotermporal chaos[J]. Science, Ner Series, 1994, 263(5153)： 1569-1570.

[3]Abdullaev F Kh. Dynamical chaos of solitons and nonlinear periodic waves[J]. Physics Reports (Review Section of Physics Letters), 1989, 179(1)： 71-78.

[4]Kodama Y, Ablowitz M J. Perturbations of solitons and solitary waves[J]. Studies in Appl. Math, 1981, 64： 225-245.

[5]Blyuss K B. Chaotic behavior of the solutions to a perturbed korteweg-devries equation[J]. Reports on Mathematical Physics, 2002, 49： 29-38.

[6]Zhang Shanyuan, Liu Zhifang, Lu Guoyun. Nonlinear flexural waves in large-deflection beams[J]. Acta Mechanica Solida Sinica, 2009, 22(4)： 287-294.

[7]Zhou Yiqing, Liu Zhifang, Zhang Shanyuan. Solitary waves and chaotic behavior in large-deflection beam[J]. Applied Mechanics and Materials, 2010, 29 (32)： 28-34.

[8]周义清， 张善元. 大挠度梁中的非线性波及其混沌行为[J]. 中北大学学报(自然科学版)， 2012, 33(6)： 643-648. Zhou Yiqing, Zhang Shanyuan. Solitary waves and chaotic behavior in a large-deflection beam[J]. Journal of North University of China (Natural Science Edition), 2012, 33(6)： 643-648. (in Chinese)

[9]周义清, 张善元. 轴压弹性圆柱壳中的非线性波及其混沌行为[J]. 中北大学学报(自然科学版)，2013, 34(4)： 346-352. Zhou Yiqing, Zhang Shanyuan. Solitary waves and chaotic behavior in an elastic cylindrical shell subjected to axial compression[J]. Journal of North University of China (Natural Science Edition), 2013, 34(4)： 346-352. (in Chinese)

[10]Melnikov V K. On the stability of the center for time periodic perturbations[J]. Trams. Moscow Math. Soc., 1963, 12： 1-57.

Nonlinear Wave and Chaos Property in Finite-Deflection Bernoulli-Euler Beam

ZHOU Yi-qing1,2, ZHANG Wei1, ZHANG Shan-yuan3

(1. College of Mechanical Engineering and Applied Electronics Technology,Beijing University of Technology, Beijing 100124, China；2. Beijing City University, Beijing 100083, China；3. Institute of Applied Mechanics and Biomedical Engineering,Taiyuan University of Technology,Taiyuan 030024, China)

Based on the finite-deflection beam theory, the nonlinear partial differential equations for flexural waves in a Bernoulli-Euler beam are derived. Using the traveling wave method and integration skills, the nonlinear partial differential equations can be converted into an ordinary differential equation. The qualitative analysis indicates that the corresponding dynamic system has a heteroclinic orbit under a certain condition. The exact periodic solution of nonlinear wave equation is obtained by means of Jacobi elliptic function expansion. The shock wave solution is given when the modulus of Jacobi elliptic functionm→1 in the degenerate case. It is easily thought that the introduction of damping and external load can result in break of heteroclinic orbit and appearance of transverse heteroclinic point. The threshold condition of the existence of transverse heteroclinic point is given by help of Melnikov function. It shows that the system has chaos property under Smale horseshoe meaning.

Bernoulli-Euler beam; finite-deflection; nonlinear wave; chaos property; Melnikov function

1673-3193(2017)01-0015-04

2015-06-29

国家自然科学基金资助项目(11402005, 11202190)； 北京市博士后科研经费资助项目(Q6001015201401)

周义清(1977-)， 女， 副教授， 博士， 主要从事非线性动力学的研究.

O347.4

A

10.3969/j.issn.1673-3193.2017.01.003