基于迭代学习理论的配电网重构*

徐 敏， 吴 成， 罗 燎， 林 辉， 戴 薇

(1. 南昌大学 信息工程学院， 江西 南昌 330031； 2. 西北工业大学 自动化学院， 陕西 西安 710072)

基于迭代学习理论的配电网重构*

徐 敏1， 吴 成1， 罗 燎1， 林 辉2， 戴 薇1

(1. 南昌大学 信息工程学院， 江西 南昌 330031； 2. 西北工业大学 自动化学院， 陕西 西安 710072)

迭代学习理论具有不依赖数学模型对期望轨迹进行零误差跟踪的特点， 将优化目标改为对目标函数轨迹的跟踪， 这样可以将其推广应用为一般的优化问题. 基于该理论的跟踪轨迹机制， 以网损最小为目标函数并考虑相应的约束条件， 采用迭代学习理论中的开环P型学习律， 通过改变网络中的开关状态进行重构， 得到网损最小的配网结构， 为配电网重构提供了一种新方法. 采用标准IEEE33， PG&E69节点系统的算例进行验证， 不仅能够求得全局最优解， 而且迭代时间由原来的1.25 s变为0.266 s.

迭代学习控制； 配电网重构； 收敛性； 网损

0 引 言

配电网重构是智能电网中自愈控制的一个重要部分， 属于大规模非线性组合优化问题. 根据国内外研究成果可将配电网重构算法大致分为以下三类： 经典数学优化方法[1]、 启发式优化方法和随机化优化方法. 其中启发式优化方法主要包括支路交换法[2]和最优流模式算法[3]， 随机化优化方法主要包括模拟退火算法[4]、 遗传算法[5]、 人工神经网络算法[6]、 禁忌搜索算法[7]、 粒子群优化算法[8]以及其他智能算法[9-10].

目前， 国内外学者在对配电网重构进行研究的过程中， 发现经典数学优化方法具有不依赖网络的初始状态和能够得到全局最优解的优点， 但计算时间很长； 启发式优化方法能够快速确定最优的网络结构和减少开关的操作次数， 但是会依赖网络的初始状态和不能保证得到全局最优解； 随机化优化方法应用算法比较广泛， 有的会产生大量的不可行解， 有的收敛性或者收敛速度不太理想， 甚至有时候会陷入局部最优. 因此， 根据自动控制理论中的迭代学习控制(Iterative Learning Control)零误差跟踪期望轨迹的特点， 本文提出了一种新的配电网重构方法， 将迭代学习理论中的开环P型学习律应用到配电网重构中. 结合基于环网的编码方式， 最小网损作为目标函数， 运用ILC算法沿着整个期望轨迹进行零误差跟踪并考虑相应的约束条件， 进而改变网络中的开关状态， 从而达到在最快的时间内来寻找全局最优解. 既解决了依赖初始网络状态的缺点、 还具有加快迭代时间和确保得到全局最优解的优点.

1 ILC与配网重构的结合

1.1 基本原理

ILC 的基本思想是： 对一个不明确模型的动态系统， 通过不断的重复迭代学习训练， 使其输出尽可能地接近期望输出的过程.

配电网重构属于离散非线性问题， 所以本文只介绍离散系统的开环P型迭代学习理论方程.

设被控系统为

(1)

式中：x(i,k)，y(i,k)，e(i,k)，u(i,k)分别表示x，y，e，u在i时刻第k次运行时的值， 其结构与参数均未知， 要求在时间i∈[0,N]内的输出y(i,k)跟踪轨迹期望输出yd(i).

输出误差为

(2)

式中：yd(i)为期望网损；y(i,k)为第k次迭代时的当前网损；e(i,k)为第k次迭代时的输出误差.

所采用的开环P型学习律算法为

(3)

式中：u(i,k+1),u(i,k)为第k+1,k次迭代时的开关组合；Γ为开环P型的常系数， 取为2.

1.2 ILC收敛性条件

ILC的收敛性问题是确保本文算法能够收敛到期望值的前提条件. 文献[11]中详细介绍了一般非线性方程式的连续和离散动态过程在开环P型学习律下学习控制过程的收敛条件， 并且给出了严格的推导证明.

根据配电网重构的离散非线性特性， ILC算法用于重构需要满足收敛的充要条件为

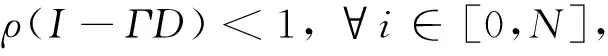
(4)

式中：Γ，D为被控系统方程式(3)和式(1)中的系数矩阵， 这里均为常系数.

1.3 ILC初值的选取

ILC初值的选取会影响到该算法收敛速度的快慢， 进而会影响收敛时间. 文献[12] 中介绍了三种选取初值的方法.

1) 通过采用控制误差死区函数来调节误差， 从而尽量使初值和期望初值保持一致.

2) 通过采用初始状态的D型迭代学习律来预测期望的初态. 此类方法不必要求初值严格在期望轨迹上.

3) 采用先前跟踪期望轨迹的经验来建立初值， 并且将这些经验轨迹保存作为期望轨迹， 从而去迭代跟踪.

由于ILC算法首次应用于重构中， 为了确保其收敛性， 将采用上述方法3)选取初值， 凭借遗传算法在配电网重构中的经验所得的输出作为期望轨迹， 再随机固定一组开关组合作为初值， 通过目标函数不断地去追踪期望轨迹， 从而达到效果.

1.4 ILC应用于配网重构的优势

ILC算法具有不需要精确的数学模型特点， 已经在电力系统抑制阻尼振荡、 控制器的设计和电力滤波器等多方面成功应用. 相比遗传算法等其他智能算法， 本文算法原理清晰， 没有复杂的算法过程， 不会产生大量的可行解， 对初始网络没有要求， 大大简化了配电网重构问题.

2 ILC配网重构

2.1 目标函数

本文对于配网的目标是减少网损， 其实现条件是安全可靠、 无孤岛以及没有闭环， 通过对配网开关状态进行改变， 选择最优的配网结构来实现网损最小， 其目标函数为

(5)

式中：Nb为网络中的支路总数；Pi和Qi分别为流过支路bi的有功功和无功功率，Ri为支路bi的支路电阻；Ui为支路bi的末端电压；ki表示开关的状态变量， 0代表打开， 1代表闭合.

2.2 约束条件

1) 潮流约束

(6)

式中：A为网络节支关联矩阵；X为线路潮流矢量；D为负荷矢量.

2) 电压约束

(7)

式中：Vi为节点i的电压；Vi min和Vi max分别为节点i电压的下限和上限.

3) 容量约束

(8)

式中：Si表示线路上i上流过功率的计算值，Si max为线路上允许通过功率的最大值.Sj表示变压器j上流出的功率，Sj max表示变压器j上允许流出功率的最大值.

4) 网络拓扑约束

配网只能开环运行， 呈辐射状， 不能存在孤立的节点.

2.3 编码方式

本文结合二进制和环网的特点来进行编码. 首先将开关状态按照二进制分为1(闭合)或0(断开)， 再根据约束条件(配电网闭环设计、 开环运行的特点)来对配电网进行分析. 为满足上述约束条件， 必须使每个环网都要断开一个开关， 才能确保辐射状.

2.4 具体步骤

以标准IEEE33节点作为算例， 介绍具体过程.

1) 输入标准IEEE33配电网网络中的5路阻抗、 节点负荷、 节点编号等原始数据. 该配网网络的节点编号采用广度优先搜索方法.

2) 针对IEEE33节点中的5个环网的开关组合进行随机初始化. 5个环网分别为L1=[2,3,4,5,6,7,33,20,19,18]；L2=[9,10,11,12,13,14,34]；L3=[8,9,10,11,35,21,33]；L4=[6,7,8,34,15,16,17,36,32,31,30,29,28,27,26,25]；L5=[3,4,5,25,26,27,28,37,24,23,22]. 通过随机函数分别对5个环网的开关随机选取， 同时要满足网络拓扑约束条件， 若不满足， 继续进行随机选取.

3) 根据2)中随机选取的开关组合在满足潮流约束的条件下对当前的辐射状网络使用前推回代进行潮流计算计算当前网损， 并将当前网损最小的开关组合、 网损存入期望存储器中， 作为当前期望值.

4) 根据2)中的开关组合建立重构模型， 进行配网重构， 计算目标函数适应度fitness. 其中电压约束和容量约束是通过罚函数加在目标函数中.

5) 首先根据适应度fitness来计算式(2)中的当前输出误差， 然后在根据开环P型迭代学习律式(3)来进行迭代.

6) 在ILC收敛条件满足式(4)条件下， 则通过u(i,k) (开关组合)重构来使y(i,k) (网损)不断地跟踪期望网损， 最后根据e(i,k)(迭代第k次和第k-1次网损之差)是否满足收敛要求输出最终结果.

7) 最后根据跟踪误差e(i,k)精度检查是否满足要求， 若满足， 将最优的开关组合存入期望存储器中并输出此时的网损； 若不满足， 将其存入期望存储器中作为下一次迭代的输入， 直到满足收敛精度为止.

ILC流程图如图 1 所示.

图 1 算法流程图Fig.1 Algorithm flow chart

3 算例分析

采用标准IEEE33和PG&E69节点系统作为算例， 将重构后的网损、 迭代时间和迭代次数与其他算法相比较， 来验证ILC算法的优越性.

3.1 算例1

标准IEEE33节点系统网络中有32条支路、 5条联络开关支路、 1个电源网络首端基准电压12.66 kV、 三相功率基准值10 mV、 网络总负荷5 084.26+j2 547.32 kVA. 配电网如图 2 所示.

图 2 IEEE33节点配电网图Fig.2 IEEE 33 nodes distribution network diagram

3.2 算例2

标准PG&E69节点系统有69个节点、 74条支路、 5个联络开关、 额定电压为12.66 kV， 网络总负荷3 802.19+j2 694.60 kVA配电网图如图 3 所示.

图 3 PG&E69节点配电网图Fig.3 PG&E69 nodes distribution network diagram

算例IEEE33， PG&E69节点系统重构前的断开开关、 网损和节点最低电压如表 1 所示.

表 1 算例原始数据

如表 2 网损结果可知， ILC算法与电流分点编码遗传算法比较， 能够实现更优的网络结构， 网损结果与IHSA算法和结合均匀变异粒子群算法相当接近， 细微的差别可能是潮流计算的方式不同引起的， 同时表明ILC算法能够得到全局最优解.

如表 3 可知ILC算法相比于比较先进的IHSA算法和结合均匀变异粒子群算法， 在得到全局最优解的基础上， ILC算法的迭代时间为0.266 s或0.484 s， 这也是该算法的最大优势.

表 2 配电网重构结果比较

表 3 迭代次数和迭代时间结果比较

4 结 论

本文从一种全新的角度出发， 采用ILC理论来研究配电网重构问题， 考虑算法的收敛性和初值的正确选取， 采用开环P型学习律来寻求网损最小的重构方案. 根据算例可知， 本文的算法用于配电网重构是有效的， 为今后将迭代学习算法应用于动态重构问题奠定了基础.

[1]王威， 韩学山， 王勇， 等．一种减少生成树数量的配电网最优重构算法[J]．中国电机工程学报， 2008， 28(16)： 34-38. Wang Wei, Han Xueshan, Wang Yong, et al. A method of reducing the number of distribution network spanning the optimal reconstruction algorithm[J]. Proceedings of the CSEE, 2008, 28(16)： 34-38. (in Chinese)

[2]Civanlar S， Grainger J J， Yin H， et al. Distribution feeder reconfiguration for loss reduction[J]. IEEE Trans. on Power Delivery， 1989， 4(2)： 1217-1223.

[3] 刘蔚， 韩祯祥. 基于最优流法和遗传算法的配电网重构[J]. 电网技术， 2004， 28(19)： 29-33. Liu Wei, Han Zhenxiang. Reconstruction based on optimal flow method and genetic algorithm distribution network[J]. Power System Technology, 2004, 28(19)： 29-33. (in Chinese)

[4]张凡， 张越喜， 顾沈卉. 基于模拟退火免疫算法的配电网重构[J]. 南方电网技术， 2011， 5(5)： 42-46. Zhang Fan， Zhang Yuexi， Gu Shenhui. Distribution network reconfiguration by simulated annealing immune algorithm[J]. Southern Power System Technology， 2011， 5(5)： 42-46. (in Chinese)

[5]段小丽， 任一峰， 赵敏. 基于遗传算法的异步电机调速系统PID参数优化[J]. 中北大学学报(自然科学版)， 2011， 32(5)： 583-587. Duan Xiaoli， Ren Yifeng， Zhao Min. Application of genetic algorithms in PID parameters optimization for asynchronous motor speed regulation system[J]. Journal of North University of China (Natural Science Edition)， 2011， 32(5)： 583-587. (in Chinese)

[6]杨帆， 毛戈. 改进人工神经网络在配电网在线重构中的研究和应用[D]. 长沙： 湖南大学， 2012.

[7]向小蓉， 刘涤尘， 向农， 等. 基于并行禁忌搜索算法的配电网重构[J]. 电网技术， 2012， 8(36)： 100-105. Xiang Xiaorong， Liu Dichen， Xiang Nong， et al. Distribution network reconfiguration based on parallel tabu search algorithm[J]. Power System Technology， 2012， 8(36)： 100-105. (in Chinese)

[8]刘科， 周继强， 郭小和. 基于改进粒子群算法的无人机路径规划研究[J]. 中北大学学报(自然科学版)， 2013， 34(4)： 441-447. Liu Ke， Zhou Jiqiang， Guo Xiaohe. Path planning research for unmanned air vehicle based on improved particle swarm algorithm[J]. Journal of North University of China (Natural Science Edition)， 2013， 34(4)： 441-447. (in Chinese)

[10]张安玲， 邓启森. 一种混合人工免疫算法的研究[J]. 中北大学学报(自然科学版)， 2015， 36(1)： 56-60. Zhang Anling， Deng Qisen. Research on hybrid artificial immune algorithm[J]. Journal of North University of China (Natural Science Edition)， 2015， 36(1)： 56-60. (in Chinese)

[11]孙明轩， 黄宝健. 迭代学习控制[M]. 北京： 国防工业出版社， 1999.

[12]林辉， 王林. 迭代学习控制理论[M]. 西安： 西北工业大学出版社， 1998.

[13]黄弦超， 杨雨. 基于电流分点编码的遗传算法在配电网重构中的应用[J]. 电力系统自动化， 2013， 37(19)： 74-79. Huang Xianchao， Yang Yu. Network reconfiguration in distribution systems based on genetic algorithm with current point technique[J]. Automation of Electric Power Systems， 2013， 37(19)： 74-79. (in Chinese)

[14]陈春， 汪沨， 刘蓓， 等. 基于基本环矩阵与改进和声搜索算法的配电网重构[J]. 电力系统自动化， 2014， 38(6)： 55-60. Chen Chun， Wang Feng， Liu Bei， et al. Network reconfiguration based on basic ring matrix and improved harmony search algorithm[J]. Automation of Electric Power Systems， 2014， 38(6)： 55-60. (in Chinese)

[15]龙军， 蒋童. 基于结合均匀变异的粒子群算法的配电网重构研究[J]. 广西大学学报(自然科学版)， 2016， 41(2)： 480-487. Long Jun， Jiang Tong. Distribution network reconfiguration based on particle swarm optimization algorithm combined with uniform mutation[J]. Journal of Guangxi University (Nat Sic Ed)， 2016， 41(2)： 480-487. (in Chinese)

Distribution Network Reconfiguration Based on Iterative Learning Control

XU Min1, WU Cheng1, LUO Liao1, LIN Hui2, DAI Wei1

(1 School of Information Engineering, Nanchang University, Nanchang 330031, China；2. School of Automation， Northwestern Polytechnical University， Xi’an 710072, China)

Since iterative learning theory has the characteristic of not rely on mathematical models for the zero error expected trajectory tracking, the optimization objective function is replaced by the target trajectory. So it can be applied to the general optimization problem. Based on the mechanism of tracking the trajectory theory, a new method for the distribution network reconfiguration was presented in this paper, with the objective function of minimum network loss and the consideration of the corresponding constraints. The open-loop P-type learning law was used to get the minimum loss distribution network by changing the switch state of network for reconstruction to get the distribution network structure with the minimum network loss. Finally, the standard IEEE33 and PG&E69 bus system were used to reconstruction which not only got the global optimal solution, but also changed the iteration time from 1.25 s to 0.266 s.

iterative learning control; distribution network reconfiguration; convergence; network loss

1673-3193(2017)01-0066-06

2015-09-26

徐 敏(1963-)， 女， 教授， 博士， 主要从事电力系统分析、 电力系统运行与控制的研究.

TM727

A

10.3969/j.issn.1673-3193.2017.01.013