大跨PC箱梁桥的预应力损失研究

汪 剑，马中文

（武汉市政工程设计研究院有限责任公司，湖北 武 汉430015）

大跨PC箱梁桥的预应力损失研究

汪 剑，马中文

（武汉市政工程设计研究院有限责任公司，湖北 武 汉430015）

预应力混凝土箱梁桥以其良好的结构整体受力性能在现代大跨桥梁结构中得到广泛应用，但迄今所修建的混凝土箱梁桥中，运营阶段箱梁开裂及下挠过大的现象较为普遍，实际混凝土箱梁桥中预应力损失估计不足是其可能的原因之一。结合某大跨预应力混凝土箱梁桥的修建及运营，对处于自然环境中的箱梁桥在纵向预应力损失作用下的确切反应进行测试，并详细地分析了各测试数据，得出了一些具有实用价值的结论，为实际箱梁桥的预应力损失分析提供参考。

预应力混凝土；箱梁；纵向预应力；预应力损失；长期测试与分析

0 引 言

大跨预应力混凝土桥梁结构在施工中的实际状态很难与设计计算分析的理论状态完全吻合，造成误差的原因是多方面的，而施工不当造成的预应力损失更引起关注，因为它将直接影响桥梁的结构强度和寿命。施工中通常采用应力和延伸量双控来监测预应力钢筋的张拉，但由于施工工艺及施工工期过短等原因，预应力索的延伸量、预应力反拱值均达不到设计要求，出现较大偏差，钢筋长度越长，表现得越明显，由此造成了纵向预应力的附加损失（即实际的损失高于设计计算时考虑的损失）[1,2]。

在现阶段的箱梁桥设计计算中，预应力第一批损失的计算一般是通过输入几个参数，即初始张拉力、预应力钢筋与管道壁的摩擦系数、管道每米局部偏差对摩擦的影响系数，以及锚具变形、钢筋回缩和接缝压缩值等，进行相应的理论计算。由于各损失的理论计算模型已得到实际工程的证实，需要说明的是对于混凝土的弹性压缩损失，由于其与预应力自身的大小有关，且该项损失相对于其他损失而言较小，因此可将其计入初始预应力中以考虑其损失。鉴于此，上述4个参数的取值成为预应力损失计算的关键问题。

本文运用人工神经网络算法（Artificial Neural Networks，简称ANN）和遗传算法（Genetic Algorithm，简称GA），并以某大跨预应力混凝土连续刚构桥施工过程的应变实测值为依据，对其预应力损失计算所采用的参数进行识别。

1 算法简介

许多复杂工程优化问题都是非线性问题，且变量之间的关系有时很难用显函数形式来表达。传统的优化方法对于复杂的优化问题很容易陷入局部最优解。遗传算法是一种全局优化算法，特别适用于多极值点的优化问题。但GA在求解时，需要反复计算目标函数值，并通过目标函数值计算适应值，来评价可行解的适应性，而复杂工程中的许多问题，很难用一个显式来表达决策变量与目标函数值之间的关系。在这种情况下，结合人工神经网络求解它们之间的关系是非常适宜的。人工神经网络具有极强的非线性映射能力，可事先不必假设数据服从什么分布，变量之间符合什么规律或具有什么样的关系。它采用类似于“黑箱”的方法，通过学习和记忆而不是假设，找出输入（决策变量）与输出（目标函数值）之间的关系（映射）。本文将GA与ANN相结合，构成GA-ANN法，协同求解复杂工程中的优化问题，利用ANN的非线性映射、网络推理和预测等功能协助GA进行优化求解。GA与ANN算法的基本原理详见相关文献[3,4]，在此不再详述。GA-ANN法计算步骤如下：

（1）定义目标函数；

（2）进行神经网络学习：本文采用BP神经网络对已收集到的一组输入即决策变量和输出（目标函数值）样本，按照BP法的步骤进行学习，建立决策变量与目标函数值之间的非线性映射；

（3）在一定的约束条件下构造初始解种群；

（4）将种群中的每一个可行解（染色体）输入给已经训练好的网络，网络将自动预测出与之对应的目标函数值，根据目标函数值计算适应值；

（5）将适应值差的染色体淘汰掉，对幸存的染色体根据其适应值的优劣，按概率随机选择，进行繁殖，形成新的群体；

（6）通过随机选择染色体进行杂交和变异操作产生子代；

（7）对子代群体重复步骤（4）～（7），进行新一轮遗传进化过程，直到找到了最优解或准最优解。

2 样本空间的建立

某悬浇预应力混凝土变截面连续刚构，跨径布置为36 m+78 m+2×120 m+78 m+36 m。主桥桥面宽29 m，分两幅修建。单幅桥为单箱单室箱形截面，箱梁高度、底板厚度均按二次抛物线变化。该桥总体布置如图1所示。

在该桥的施工过程中，对其进行了各主要工况下的应变监测，由此可以得到各梁段张拉预应力前后T构根部截面的应变变化，由于测试数据较多，在此仅给出各墩上下缘的平均数据（由于测试前后时间间隔较短，因此可以认为数据中不包含混凝土收缩徐变的影响），如图2～图4所示（图中负值为压应变）。

图1 某大跨PC连续刚构桥总体布置图（单位：cm）

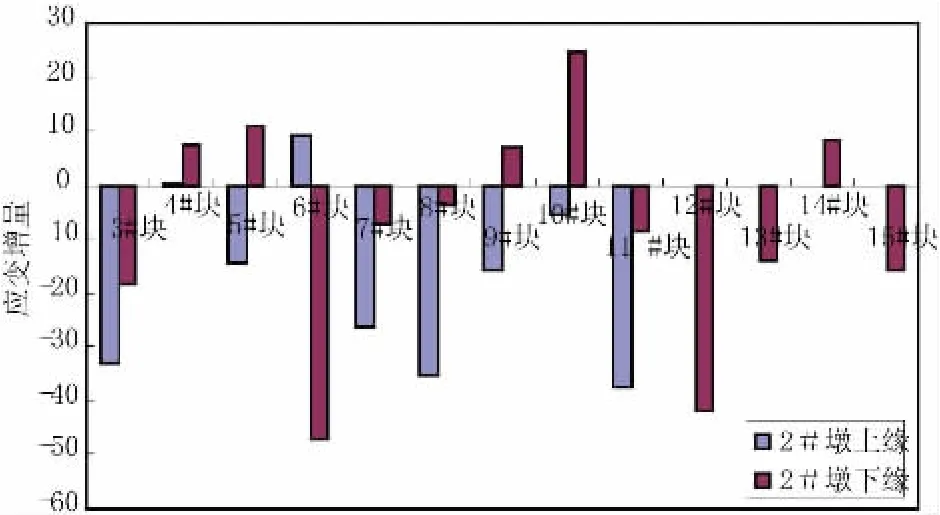
图2 2＃墩张拉预应力前后根部截面应变变化（单位：με）

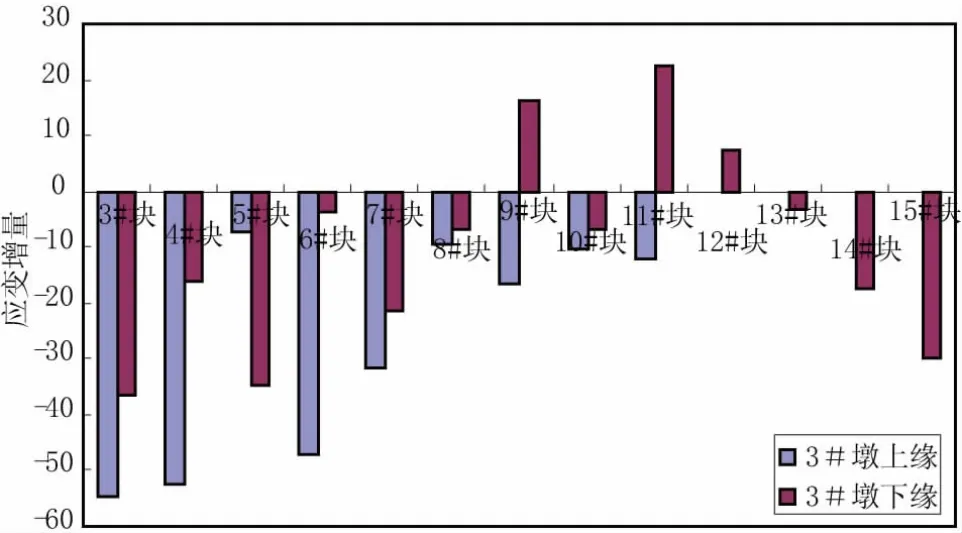
图3 3＃墩张拉预应力前后根部截面应变变化（单位：με）

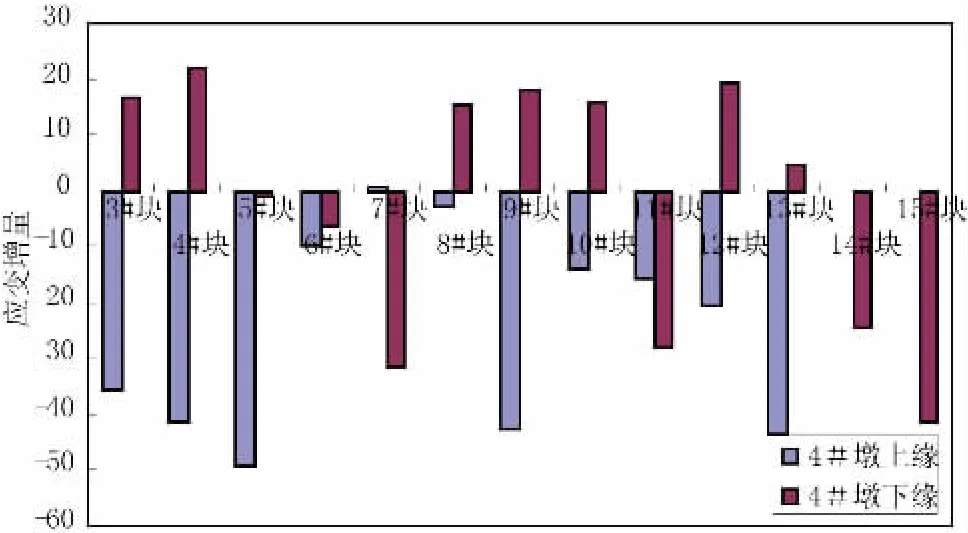
图4 4＃墩张拉预应力前后根部截面应变变化（单位：με）

由于引起上述应变实测值与理论值存在差异的原因除预应力损失外，还包括混凝土弹性模量和箱梁截面参数（如截面面积、惯性矩）的影响，因此本文识别的参数包括混凝土弹性模量、箱梁截面参数（考虑到施工中箱梁顶板的厚度误差相对较大，本文取箱梁顶板厚度作为具体的识别参数，以反应截面面积及惯性矩的影响）、初始张拉力、预应力钢筋与管道壁的摩擦系数、管道每米局部偏差对摩擦的影响系数以及锚具变形、钢筋回缩和接缝压缩值等6个参数，设定一个取值范围(见表1)。

各参数在取值范围内分别取3～5个值后进行排列组合，然后将各组参数数据输入有限元模型进行计算，可以得到各组参数对应的应变变化值，并取目标函数为：

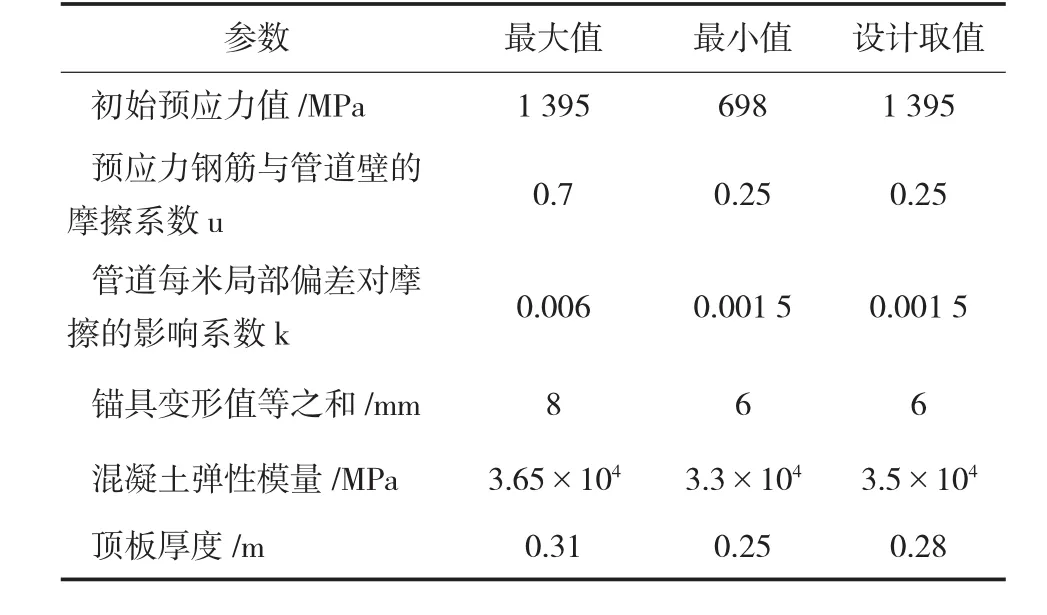
表1 各参数取值范围

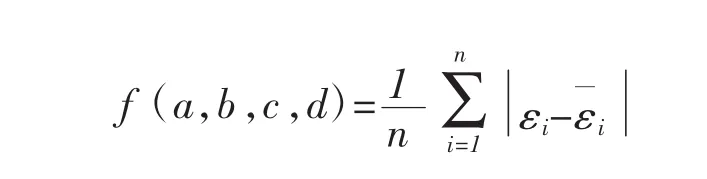
式中：εi为实测值；ε¯i为有限元计算值，计算后即可得到各墩的样本空间。

3 参数识别结果及分析

将各墩样本空间数据合并后输入GA-ANN模型中，即可得到各参数的识别值，为计算方便，本文将识别出的后5个参数，即混凝土弹性模量、顶板厚度、预应力钢筋与管道壁的摩擦系数、管道每米局部偏差对摩擦的影响系数，以及锚具变形、钢筋回缩和接缝压缩值取为定值，并作为约束条件与各墩的样本空间再次输入GA-ANN模型中，得到各墩的初始张拉力，其结果见表2。

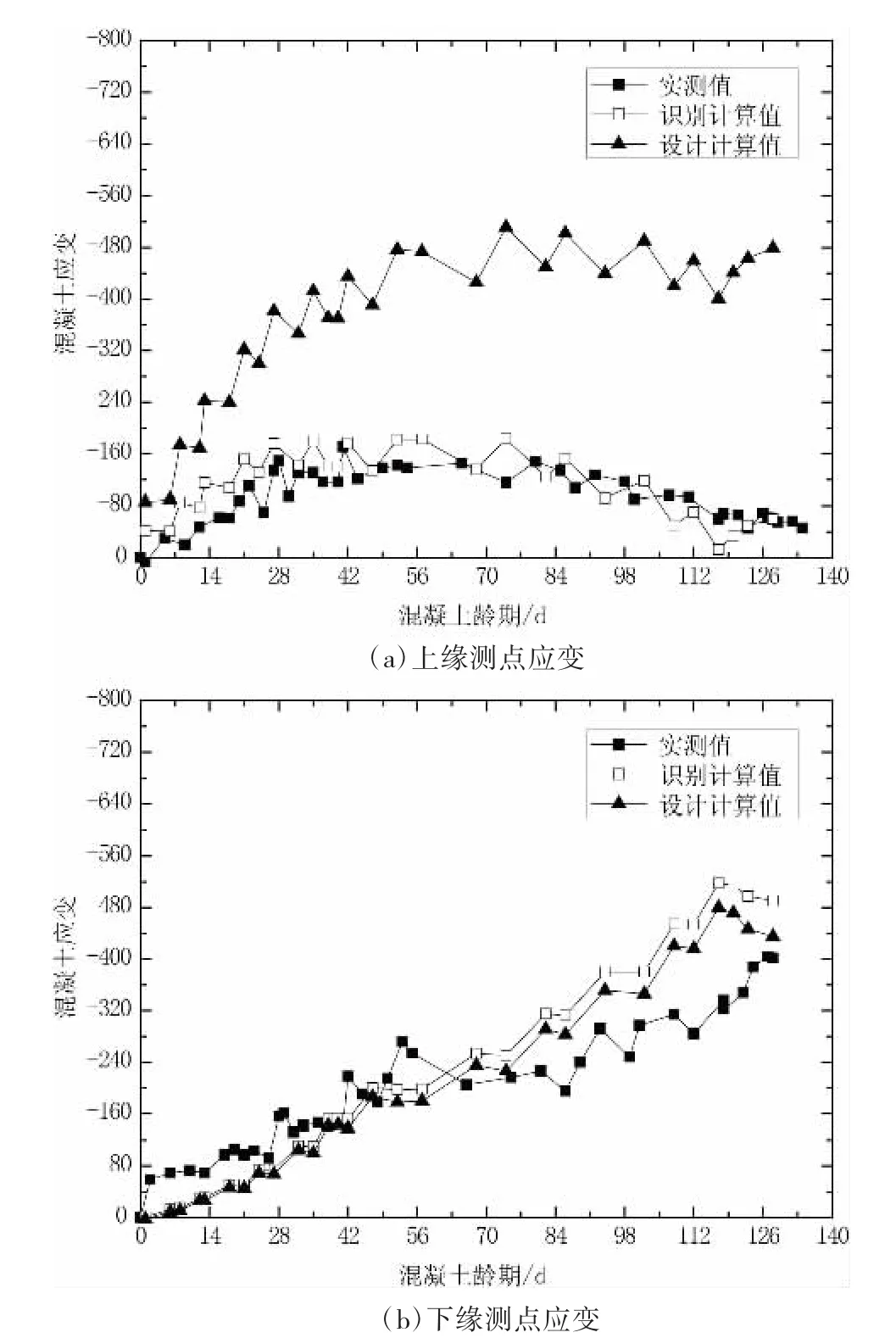
图5 2＃墩S2截面应变变化（单位：με）

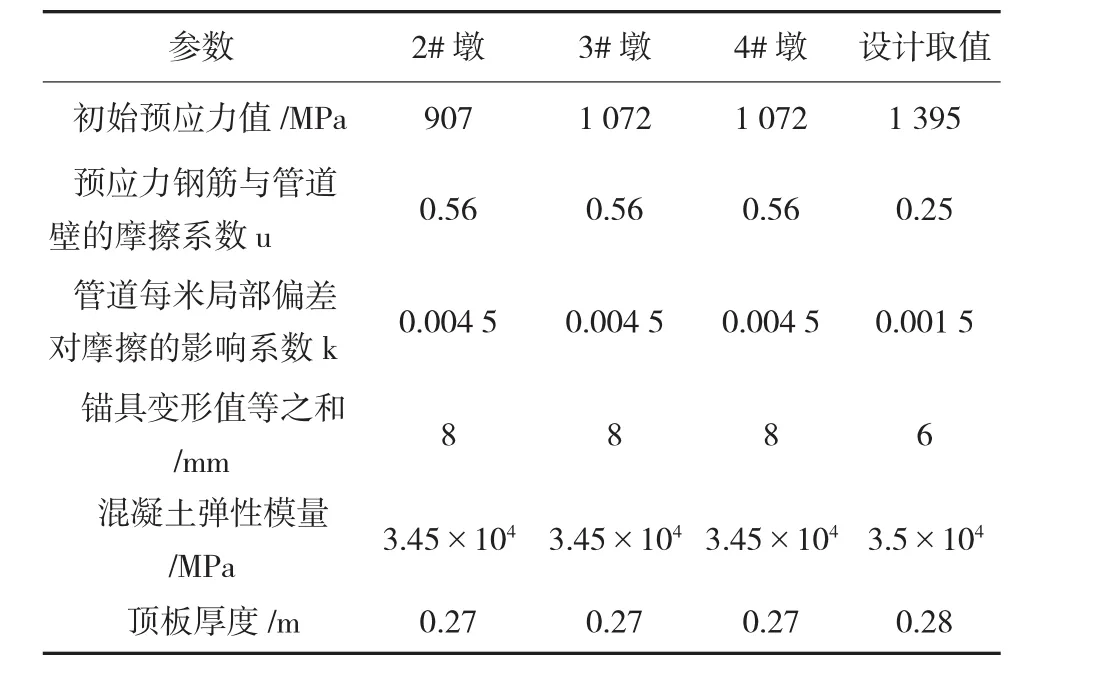
表2 各参数识别结果

将以上参数识别值输入有限元模型后，对该桥进行施工阶段分析，其计算结果如图5～图8所示。

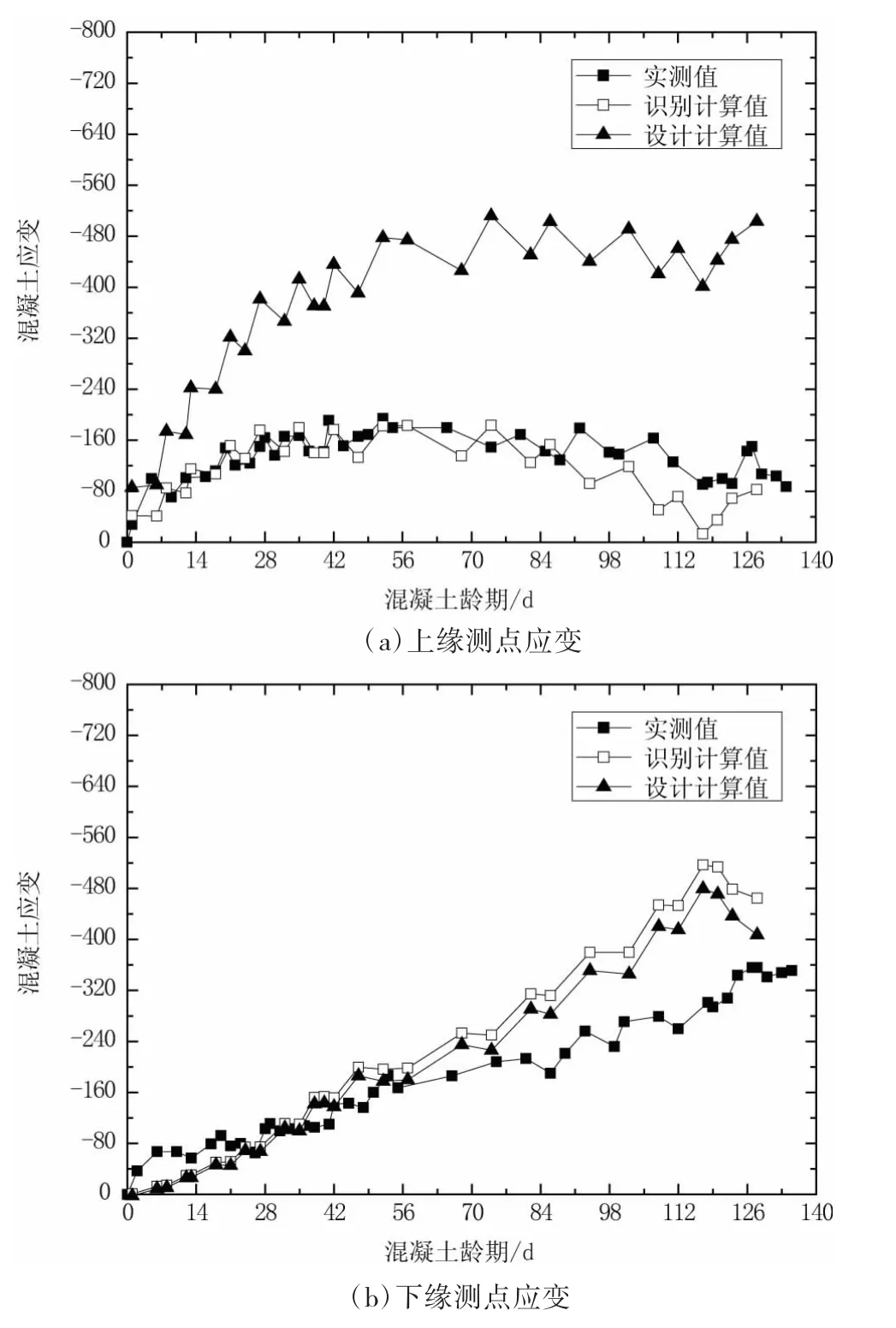
图6 2＃墩S3截面应变变化（单位：με）

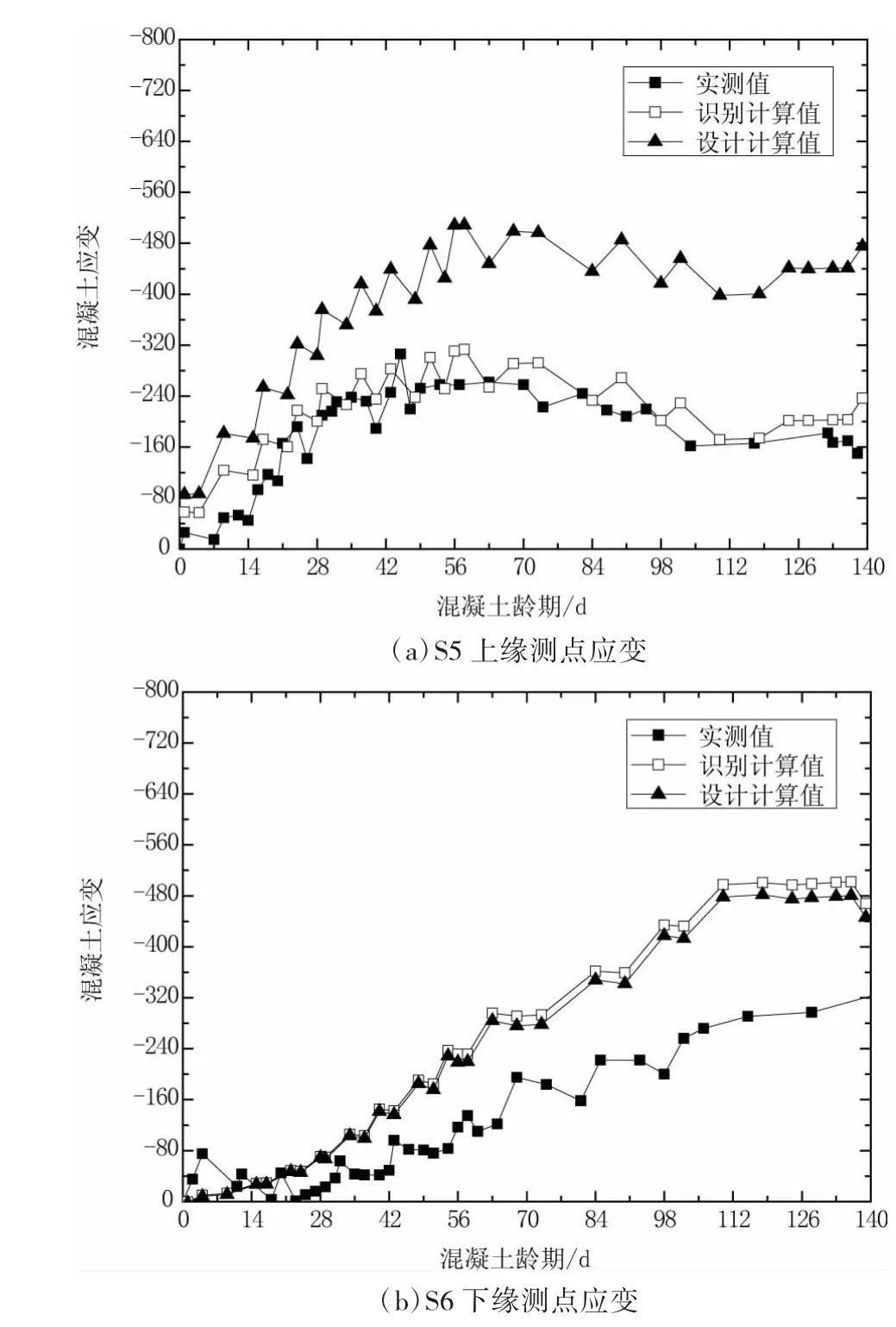
图7 3＃墩S5、S6截面应变变化（单位：με）

从图5～图8中可以看出，特别是对于各根部截面上缘测点，采用识别出的参数计算出的结果与实测值吻合较好，而此时采用表2中设计值计算的结果与实测值相差较大，而对于截面下缘测点，采用识别出的参数计算出的结果与实测值大致吻合，表明识别出的第一批预应力损失值更为准确地描述了实际情况。

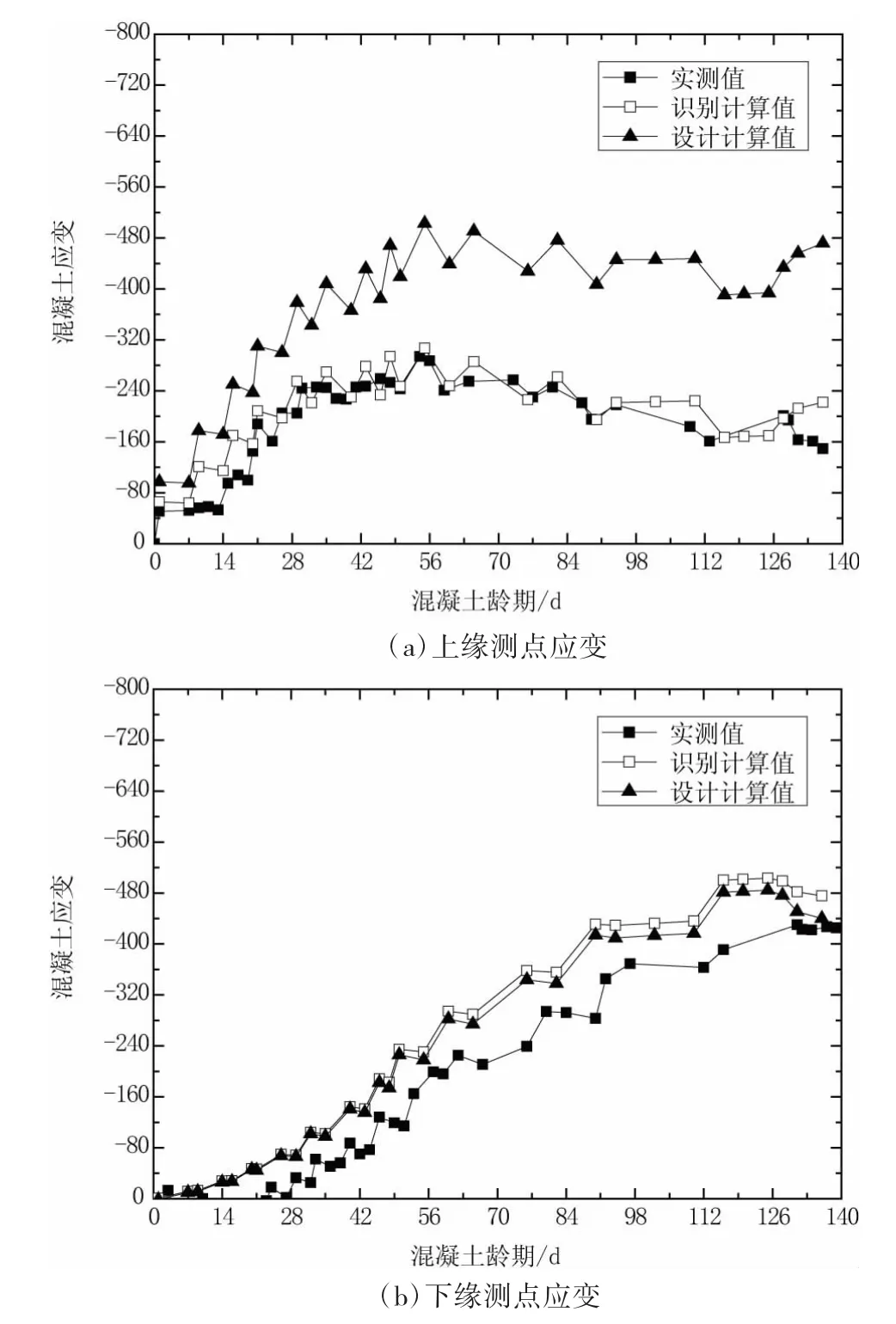
图8 4＃墩S9截面应变变化（单位：με）

由于以上识别是对该桥前期预应力束的整体考虑，以致由识别出的参数所计算出的单项损失（如摩擦损失、锚固损失等）不可能完全反应预应力钢筋的实际情况，但由各参数计算出的总损失能够反应该桥的第一批预应力损失水平，因此本文采用表2中的相关参数对2＃墩、3＃墩的典型顶板束进行预应力损失计算，其计算结果见表3。

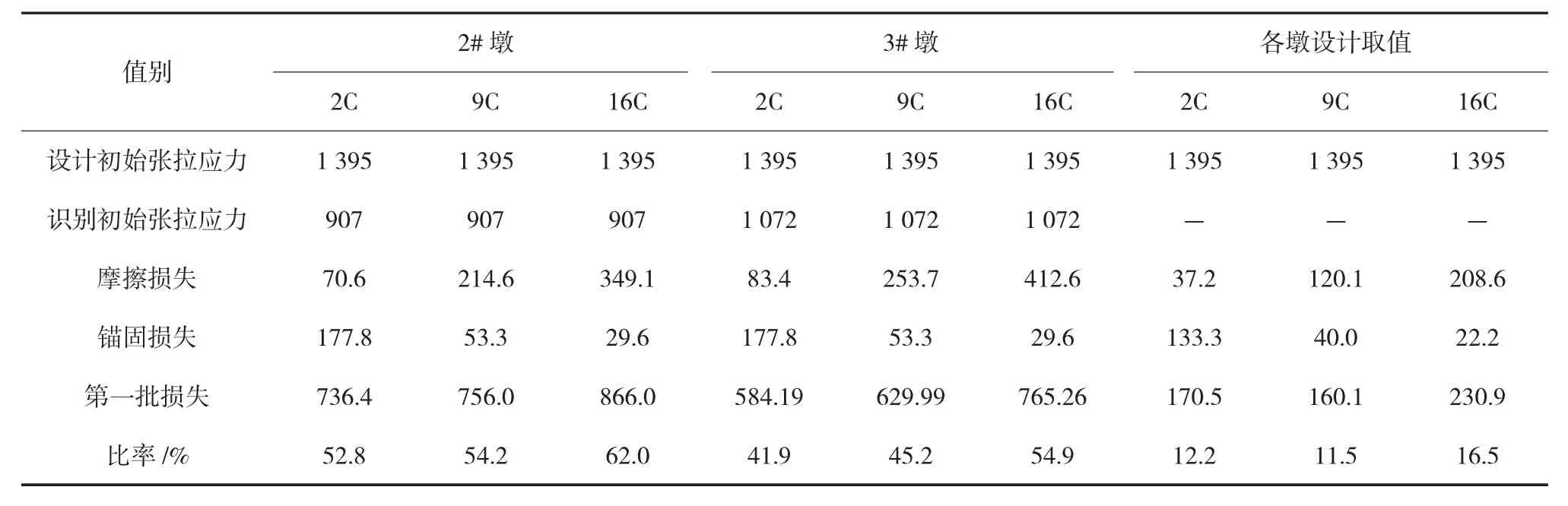
表3 各墩顶板束第一批预应力损失计算结果 MPa

从表3中可以看出，该桥的预应力损失非常严重，仅第一批损失就占到设计初始预应力的40%之多，而按照设计取值，其损失仅为设计初始预应力的11%～17%，两者相差较大。究其原因，可能主要是由于施工方面的原因如张拉不到位、混凝土龄期过短就进行预应力筋的张拉，预应力筋孔道偏差较大等造成的，因此在混凝土箱梁桥的施工过程中，应加强施工质量的管理，不能过分强调施工速度而缩短混凝土的养护龄期，以尽量避免由于施工的原因造成设计计算中没有考虑的预应力损失。

4 结 论

本文基于某桥施工过程的应变测试数据，对纵向预应力第一批损失进行了分析，得出以下结论：就所分析的结果而言，该桥纵向预应力损失较为严重，仅第一批损失就占到设计初始预应力的40%之多，因此应加强施工质量的管理，尽量避免由于施工的原因造成设计计算中没有考虑的预应力损失。

[1]沈成武，闻骥骏，黄志刚.大跨度桥梁预应力损失的遗传算法识别[J].武汉理工大学学报，2002，24(1)：62-65.

[2]刘志文，宋一凡，赵小星.空间曲线预应力束摩阻损失参数[J].西安公路交通大学学报，2001，21(3)：42-44.

[3]李晓峰，刘光中.人工神经网络BP算法的改进及其应用[J].四川大学学报，2000，32(2)：105-109.

[4]张建仁，刘杨.遗传算法和人工神经网络在斜拉桥可靠度分析中的应用[J].土木工程学报，2001，34(1)：7-13.

[5]JTG D62-2004，公路钢筋混凝土及预应力混凝土桥涵设计规范[S].

[6]汪剑.大跨预应力混凝土箱梁桥非荷载效应及预应力损失研究[D].长沙：湖南大学，2007.

[7]王英，刘建新，赵人达.大跨桥梁预应力损失综合值法计算模型研究[J].世界桥梁,2011(5):48-51.

[8]李准华，刘钊.大跨度预应力混凝土梁桥预应力损失及敏感性分析[J].世界桥梁,2009(1):36-39.

[9]朱琛.预应力高性能混凝土桥的预应力损失比较[J].世界桥梁,

2010(3)：23-27.

[10]张秋陵，肖光宏.塑料波纹管与铁皮波纹管摩阻系数对比分析[J].世界桥梁,2010(3)：47-49.

山东高速公路将建成“9517网”

经山东省政府同意，省发展改革委、省交通运输厅组织编制了《山东省高速公路网中长期规划（2014-2030年）调整方案》，重点对部分项目的建设时序、规划线位等做出局部调整，调整后的方案日前印发。根据新方案，全省高速公路网布局为“九纵五横一环七连”（简称“9517网”），总里程约8 300 km。

9条纵线包括：烟台-日照（鲁苏界）；潍坊-日照；无棣（冀鲁界）-青州-临沭（鲁苏界）；沾化（冀鲁界）-淄博-临沂（鲁苏界）；无棣（冀鲁界）-莱芜-台儿庄（鲁苏界）；乐陵（冀鲁界）-济南-临沂（鲁苏界）；德州（冀鲁界）-泰安-枣庄（鲁苏界）；德州-东阿-单县（鲁皖界）；德州（冀鲁界）-商丘（鲁豫界）。

5条横线包括：威海-德州（鲁冀界）；青岛-夏津（鲁冀界）；青岛-泰安-聊城（鲁冀界）；董家口-范县（鲁豫界）；日照-菏泽-兰考（鲁豫界）。

1条环线为：威海-烟台-潍坊-东营-滨州-德州-聊城-菏泽-济宁-枣庄-临沂-日照-青岛-烟台-威海。

7条连接线包括：烟台-海阳；龙口-青岛；荣成-潍坊；东营-济南-聊城-馆陶（鲁冀界）；济南-菏泽-商丘（鲁豫界）；济南-徐州（鲁苏界）；濮阳-阳新（山东段）。

此外，为进一步加强山东省东西部乃至与我国中西部地区联系，拓展山东省经济发展腹地，形成山西中南部经河南连接董家口港区的集疏运大通道，新调整方案将原研究线位梁山至五莲列入规划线位并纳入实施序列。

U448.21+3

A

1009-7716（2017）01-0140-05

10.16799/j.cnki.csdqyfh.2017.01.041

2016-11-16

汪剑（1979-），男，湖北罗田人，工学博士，高级工程师，从事桥梁设计工作。