大跨径预应力混凝土梁桥孔道摩阻试验研究

赵康，魏洋，端茂军，李国芬

(南京林业大学土木工程学院，南京210037)

大跨径预应力混凝土梁桥孔道摩阻试验研究

赵康，魏洋，端茂军，李国芬

(南京林业大学土木工程学院，南京210037)

为更精确地进行施工监控，结合某三跨连续梁桥，通过现场试验得出实际孔道摩阻系数。对实测得到的短、长预应力束的摩阻系数和管道偏差系数对比分析，并根据实测数据修正有限元模型，对比分析修正后支座截面顶板的应力理论计算值与现场实测值。试验得出不同长度预应力束的摩擦系数μ分别为0.254和0.282，偏差系数k分别为0.002 0和0.001 7。结果表明，实际施工过程中的摩阻系数大于规范上限值1.6%～33.3%，不同长度的预应力束的摩阻系数存在较大离散性，随着预应力束的增长，曲线处由于法向挤压力导致的摩阻损失占整体预应力摩阻损失的比重增加，长束预应力束相比较短束μ值增加了11%，k值减小了15%。支座截面顶板应力实测值与理论计算值变化趋势一致，采用实测值修正后误差减小，两次修正误差分别减少了10%和9%。

预应力；连续梁桥；摩阻试验；摩阻系数；施工监控

混凝土连续梁桥由于结构受力合理、施工工艺成熟等优点广受欢迎。混凝土连续梁桥的预应力损失计算直接关系到成桥后的线形与受力情况，对于预应力损失的错误估计将会直接导致连续梁桥应力储备不足，进而导致梁体跨中下挠、腹板开裂[1]。经国内学者整理分析,设计施工不合理是桥梁事故发生的主要原因[2-3]。目前公路桥规中规定了预应力损失的6个主要原因，其中孔道摩阻损失是主要损失部分，有研究[4-5]表明摩阻损失占预应力总损失的20%～77%，其中合龙束的摩阻损失占预应力总损失的40%～50%，而对于T型悬臂结构中的预应力束其摩阻损失高达总损失的62%～77%[6]。

管理学生档案时，如果是需要单一或少数学生的信息，可以采取复制与粘贴的方法。如果要从全院所有学生数据表中查找一个班或者一个系部的几十或几百余人信息，便可利用VLOOKUP函数来处理，不仅节省工作量，而且确保数据的准确性。

孔道摩阻损失是指预应力筋与周围接触的混凝土或套管之间发生摩擦造成的应力损失。摩阻损失的大小与张拉时的材料、锚具类型、现场施工水平、张拉工艺以及周围环境具有较大的相关性。Barr等[5]指出高性能混凝土摩阻损失大于常规混凝土；Garber等[7]通过研究30片预制梁在不同气候条件下的预应力损失，提出了几种不同的预应力损失量化估计模型；Caro等[8]研究了不同配合比、梁体截面尺寸以及不同张拉时间下的先张法预应力混凝土的摩阻损失，提出了混凝土梁实测受力与预应力损失系数计算模型；Lundqvist等[9]研究了不同温度、湿度以及混凝土不同徐变预测模型对预应力摩阻损失的影响，并提出徐变的影响占主导地位。规范中采用σcon[1-e-(μθ+kx)]来初步计算摩阻损失，对于计算公式中摩阻系数μ和管道偏差系数k的规定，以金属波纹管为例，国内外各规范的取值相差较大(国内规范为《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62—2004)下文简称公路桥规、《铁路桥涵钢筋混凝土和预应力混凝土设计规范》(TB 10002.3—2005)下文简称铁路桥规、《混凝土结构设计规范》(GB 50010—2010)下文简称混规)，具体数值如表1所示。

表1 国内外各规范中对孔道摩阻系数的取值

孔道摩阻损失的精确估计对于桥体性能的影响，很早就引起了学者与工程界的重视。众多学者都进行了现场张拉试验，得出实际孔道摩阻系数结果都接近公路桥规最高限值或超过最高限值[10-11]。张开银等[12-13]基于接触应力理论研究了非连续弯曲孔道所产生了摩擦力矩，提出弯曲孔道与预应力束接触面间的正压力分布不仅与张拉力大小有关，还与接触物体弹性模量和曲率半径等因素有关。肖财等[14]在张开银基础上通过CT扫描进行了模型试验，指出目前规范中对于非连续弯曲部分摩阻损失的计算较为粗糙。张文学等[15]研究了钢束参数对于摩阻测试的误差敏感系数的影响规律并在对比分析两种孔道摩阻测试方法的基础上得出测试钢绞线长度应大于15 m，弯曲角度不宜小于3°的结果。Cho等[16]通过理论数值计算分析了预应力束长度、螺旋角度以及横截面积对预应力束应力分布的影响，拟合出了一项应力计算公式。Jeon等[17]将孔道摩阻测试误差产生原因归结于传统的电阻应变传感器，同时设计了一款碳纤维增强聚合物光纤光栅传感器来代替原预应力束中的一股钢束。相对于同一工程中的单一长度预应力筋孔道摩阻的现场试验，对于同一工程中不同长度预应力筋的摩阻系数尚缺乏研究。本研究采用公路桥规(JTG D62—2004)中的孔道摩阻计算公式，利用最小二乘法对不同长度的预应力束的孔道摩阻进行试验分析。通过实测值对施工进行阶段误差修正，从而实施有效精确的施工监控，对成桥线性及受力满足设计要求具有指导意义。

1 工程概况

某预应力混凝土连续梁桥为三跨变截面结构，跨径组合为(75+120+70)m预应力混凝土连续箱梁。箱梁顶宽15 m，底宽8 m，梁高由跨中3.2 m变化至距主墩中心处7 m，箱梁在横桥向底板保持水平，箱顶设2%双横坡，见图1和图2。预应力体系采用纵、横、竖三向预应力设计。预应力钢束采用ΦS15.2高强度低松弛钢绞线，预应力管道采用预埋金属波纹管，采用挂篮悬臂浇筑法对称施工。

图1 梁桥整体结构图Fig. 1 Integral structure diagram of the bridge

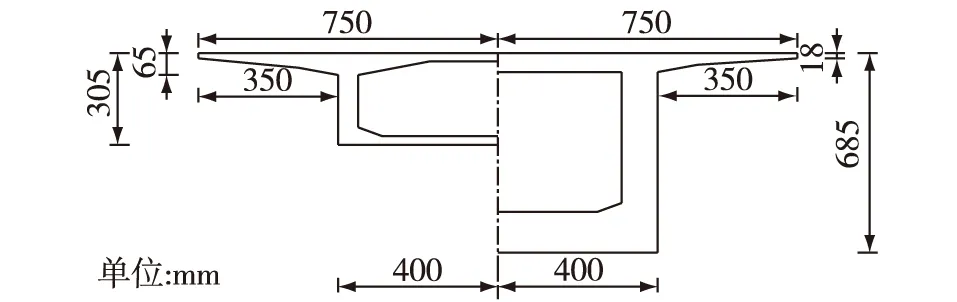
图2 箱梁跨中及支点横断面图Fig. 2 Cross-sectional profile of midspan and pivot

2 试验准备

根据表3数据可以发现，试验实测孔道摩阻系数μ及偏差系数k值与公路桥规规定值之间存在差异，而且实测值均比规范值大，这表明实际施加在桥体上的预应力小于设计值，会对桥体的受力情况及线性产生不利影响，理应采取修正措施。本试验短束μ实测值超规范上限值1.6%，长束μ实测值超规范上限值12.8%，短束k实测值超规范值33.3%，长束k实测值超规范值11.7%。同时可以看出，在同一项目当中不同长度的预应力束的摩阻系数存在较大离散型，长束预应力束相比较短束μ值增加了11%，k值减小了15%，这也表明μ值所占的影响比重随预应力束的增长而增大，k值则是减小，即随预应力束的增长曲线处由于法向挤压力导致的摩阻占整体预应力摩阻损失的比重增加。

试验预应力钢束中短束选取悬浇段3#块的腹板束W3-1、W3-2以及顶板束D3-1、D3-2，短束W3和D3长度均为24 m，总转角分别为0.926 rad和0.330 rad；长束选取悬浇段14#块的D14-1、D14-2、D14′-1和D14′-2，长束D14和D14′长度均为102 m，总转角分别为0.536 rad和1.200 rad。规格如图4所示。

图3 压力传感器标定数据图Fig. 3 Calibration data of pressure sensor

3 孔道摩阻测试

孔道摩阻主要有两种形式：一是由于曲线处钢束张拉时对孔道壁施以法向正压力而引起的摩擦，阻力较大；另一是由于孔道偏差致使接触面增多，从而引起摩擦阻力，其值一般相对较小。前者的大小反映了孔道与预应力筋两种材料之间的接触力学性质，而后者则反映了孔道施工的质量。

图5 孔道摩阻试验示意图Fig. 5 Schematic diagram of channel friction test

3.1 试验原理

本试验主要通过压力传感器测定孔道张拉束主动端与被动端实测压力值，根据规范规定的公式计算偏差系数k和摩擦系数μ。张拉时，预应力束距固定端距离为x的截面上有效拉力为：

用SPSS 19.0软件对三种方法检测结果以Duncan法进行oneway-ANOVA分析，比较3组结果是否存在显著差异。无显著差异则继续进行3组样本间相关性分析，检验两种快检法检测结果与国家标准方法的相关程度，比较何者相关性更好。以原吸法结果为自变量建立两种快检法对于原吸法结果的线性回归方程，确定快检法与原吸法契合程度较高的检测范围。

F1=F2e-(μθ+kx)

(1)

A=Fx/Fk=e-(μθ+kx)

(2)

施工过程中应力的监控是必不可少的，笔者采用MIDASCIVIL 2013进行全桥仿真模拟计算，荷载考虑恒载、二期恒载、预应力、混凝土收缩徐变和温度升降。全桥模型采用梁单元模拟计算。根据有限元计算结果，箱梁支座等截面为梁桥T型结构施工过程中应力最大截面。该截面处的应力大小是设计及施工过程中重要的控制量。通过对该截面顶板在各个节段浇筑及预应力张拉后的应力进行分析处理，并与设计理论值及修正理论值对比，图6为支座处截面顶板从1#块浇筑至16#预应力张拉32个施工工况下的应力统计情况(应力正值为拉应力，负值为压应力)。整个施工过程分为3个阶段，第Ⅰ阶段为0#块浇筑至3#块张拉，此时摩阻损失采用公路桥规给出值(μ=0.250，k=0.001 5)进行计算，第Ⅱ阶段为3#块张拉完至14#块张拉完，此时预应力损失计算采用短束摩阻测试值(μ=0.254，k=0.002 0)，第Ⅲ阶段为14#块张拉完至中跨合龙，此时摩阻系数采用长束摩阻系数测试值(μ=0.282，k=0.001 7)。

排除标准：（1）继发性帕金森病患者；（2）药物滥用史患者；（3）认知功能障碍患者；（4）妊娠或哺乳期女性患者；（5）恶性肿瘤患者；（6）未遵循医嘱服药的患者；（7）严重重要脏器功能不全的患者；（8）近期服用过可能引起锥体外系不良反应的药物。

解方程组即可得μ、k值。

HU Yi-jun, LIU Shu-peng, CHENG Kai, XU Gui-xia, HU Jing-jing, LIU Shan-rong

(3)

(4)

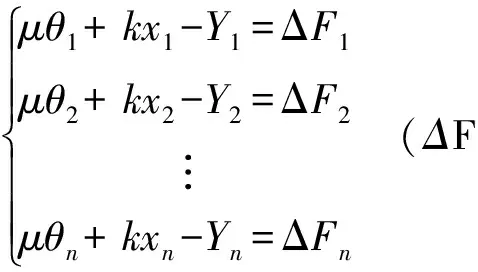
试验首先在预应力束两端安装压力传感器和千斤顶，具体布置图如图5所示。在试验开始时，预应力束两端同时张拉至设计张拉控制荷载的5%，然后将预应力束一端封闭作为被动端，以另一端作为主动端，分级加载至设计张拉控制荷载。每级荷载到位后，读取两端传感器读数。然后再根据两端传感器读数，具体数值如表2所示。

穿心式压力传感器是根据预应力束的设计张拉吨位和直径制作了相应规格，并分别在压力试验机上进行了标定。标定结果如图3所示，结果表明，在试验过程中当荷载达到最大(3 200 kN)时，压力传感器仍在弹性阶段，数据线性回归系数R2均为1.0，荷载和应变存在良好的线性关系。同时本传感器具有针对性强、可重复加工使用等优点。

图4 试验预应力束Fig. 4 Tested prestressing tendons

3.2 试验内容和方法

表2 孔道摩阻系数计算表

注：表中F为设计张拉控制荷载。

3.3 试验结果分析

试验时通过传感器读取荷载值后，即可将数据代入3.1节的公式中，由D3、W3计算短束D14、D14′计算长束的μ及k值，并将实测值与规范和其他同类型进行比较，如表3所示。

表3 孔道摩阻系数的实测值

本试验使用了千斤顶、高压油泵、压力传感器4套(配套连接线缆)、TDS-530数据采集仪、工具锚、工作锚、配套限位板等仪器。

造成实测值与理论规范值差异的主要原因可能为波纹管的孔道成型不达标，孔道定位不够准确或者受到外界因素的影响发生偏移而造成孔道不顺直，特别是在节段连接处易产生一定的转角导致摩擦阻力增加。

4 监控模型修正及应力分析

式中：F1为固定端截面预应力束拉力，kN；F2为张拉端预应力束的拉力，kN；θ为张拉端至计算截面孔道弯角和，rad；x为从张拉端至计算截面孔道长度，m；A为预应力有效系数。此时则有：-lnA=μθ+kx，再令Y=-lnA，由此对于同一片梁不同孔道的测量可得：

由图6可见，出实测应力值与理论计算及修正值变化趋势一致(实测值小于计算值)。在第Ⅱ阶段可以看出，摩阻系数采用μ=0.254、k=0.002 0时理论计算值介于实测值与规范上限计算值之间，经统计，在第Ⅱ阶段规范计算值与实测值误差为4%～22%，修正过后理论计算值与实测值误差为2%～12%。在第Ⅲ阶段，摩阻系数采用μ=0.282、k=0.001 7时理论计算值介于实测值与第一次修正计算值之间，经统计，在第Ⅲ阶段规范计算值与实测值误差为9%～12%，第一次修正理论计算值与实测值误差为5%～8%，第二次修正理论计算值与实测值误差在1%～3%。可以看出每一次修正均使理论计算值更接近实测值，第一次修正误差减少了10%、第2次修正误差减少了9%，有效地提高了计算精度。

“你把这个带去吧！放在包袱里，别叫人给你抢去，娘一个钱也没有。若饿肚时，你就去卖掉，买个干粮吃吧！”走出门去还听母亲说：“遇见日本子，你快伏在蒿子下。”

“秦月”由“秦富1号”和“嘎拉”杂交育成。果实呈圆形或长圆锥形，大小均匀，果个与嘎拉接近，果皮鲜红，果肉黄白，肉质细脆多汁，酸甜适口，较耐贮存。在渭北高原南部地区8月底成熟，渭北高原中部地区9月上中旬成熟，刚好赶上中秋节和国庆节，是一个优良的中熟苹果新品种。

图6 支座截面顶板应力Fig. 6 Roof stress of bearing cross section

5 结 论

本研究结合某预应力连续梁桥，通过现场试验得出孔道摩阻系数，分析实测数据并修正有限元模型，对比分析修正前后支点截面应力。得出以下结论：

1)实际工程当中预应力摩阻损失由于现场环境复杂，实际损失值往往大于理论计算值，试验实测得出摩阻系数μ=0.254且k=0.002 0(短束)、μ=0.282且k=0.001 7(长束)，结果均大于规范值μ=0.20～0.25且k=0.001 5，μ与k最大超出规范限值分别为12.8%和33.3%。

2)相同项目现场选择测试束时应选取相近束长的进行测试分析计算，对比现场长短束的实测结果得出单组摩阻试验应选取预应力束长相近进行试验，不同束长的摩阻系数有着较大的离散性，随着预应力束的增长μ对预应力损失的影响越加明显。

本文采用的扎根理论以及网络文本分析法，主要依据笔者自己的分析，网络文本分析的内容是根据网上的游客短评与游客游记进行处理的，这类评论尽管数量比较多、获取容易，但也存在一些讨论主题模糊不清、短评内容不符合研究主题以及旅游者主体不明确等问题。根据分析内容得出的营销策略选择，只是对神农谷国际森林公园发展的一种建议。也会有其他很多营销策略选择，本文没有进行更多的探究，可能会存在不足。

3)预应力摩阻的损失不会改变梁体的应力分布，现场应力实测值与理论计算值变化趋势一致(实测值小于计算值)，通过现场测试得出摩阻系数实测值可以减小误差更为精确的施工监控，根据现场实测的摩阻系数修正计算值可以有效地减小误差，最小可缩减至1%～3%。

[1]郭振武, 彭楠楠. 预应力混凝土箱梁孔道摩阻损失测试[J]. 公路, 2010(12):60-67. GUO Z W, PENG N N. Test of prestressed concrete box girder channel friction loss[J]. Highway, 2010(12):60-67.

[2]吉伯海, 傅中秋. 近年国内桥梁倒塌事故原因分析[J]. 土木工程学报, 2010(S1):495-498. JI B H, FU Z Q. Analysis of Chinese bridge collapse accident causes in recent years[J]. China Civil Engineering Journal, 2010(S1):495-498.

[3]徐洪涛, 郭国忠, 蒲焕玲, 等. 我国近年来桥梁事故发生的原因与教训[J]. 中国安全科学学报, 2007, 17(11):90-95. XU H T, GUO G Z, PU H L, et al. Causes and lessons of bridge accidents in China in recent years[J]. China Safety Science Journal, 2007, 17(11):90-95.

[4]李准华, 刘钊. 大跨度预应力混凝土梁桥预应力损失及敏感性分析[J]. 世界桥梁, 2009(1):36-39. LI Z H, LIU Z. Analysis of prestressing loss and sensitivity of long span prestressed concrete beam bridge[J]. World Bridges, 2009(1):36-39.

[5]BARR P J, KUKAY B M, HALLING M W. Comparison of prestress losses for a prestress concrete bridge made with high-performance concrete[J]. Journal of Bridge Engineering, 2008, 13(5):468-475.

[6]王涛, 钟穗东, 张汉平. 预应力孔道摩阻系数测试与分析[J]. 公路, 2010(5):35-38. WANG T, ZHONG S D, ZHANG H P. Test and analysis of prestressed duct friction factor[J]. Highway, 2010(5):35-38.

[7]GARBER D B, GALLARDO J M, DESCHENES D J, et al. Experimental investigation of prestress losses in full-scale bridge girders[J]. ACI Structural Journal, 2015, 112(5):553.

[8]CARO L A, MART-BARGAS J R, SERNA P. Prestress losses evaluation in prestressed concrete prismatic specimens[J]. Engineering Structures, 2013, 48:704-715.

[9]LUNDQVIST P, NILSSON L O. Evaluation of prestress losses in nuclear reactor containments[J]. Nuclear Engineering and Design, 2011, 241(1):168-176.

[10]王强, 何惟煌, 林志春, 等. 后张预应力混凝土梁管道摩阻参数识别与分析[J]. 公路交通科技, 2007, 24(1):65-68. WANG Q, HE W H, LIN Z C, et al. Parameter identification and analysis of tube friction resistance loss in the post-tensioned pre-stressed concrete girders[J]. Journal of Highway and Transportation Research and Development, 2007, 24(1):65-68.

[11]刘喜元, 陈玉骥, 罗旗帜, 等. 惠州下角东江大桥钢绞线孔道摩阻预应力损失的试验研究[J]. 中外公路, 2008, 28(2):133-136.

[12]张开银, 顾津申,张军辉, 等. 弯曲孔道摩阻预应力损失试验研究[J]. 武汉理工大学学报 (交通科学与工程版), 2009, 33(2):306-309. ZHANG K Y, GU J S, ZHANG J H, et al. Experimental study about prestressing loss of strand caused by frictional resistance in curving hole[J]. Journal of Wuhan University of Technology(Transportation Science & Engineering), 2009, 33(2):306-309.

[13]张开银, 郭志伟, 顾津申. PC 弯曲孔道摩阻预应力损失试验与分析[J]. 中外公路, 2010, 30(4):145-149. ZHANG K Y, GUO Z W, GU J S. Test and analysis of PC curved hole friction loss of prestress[J]. Journal of China & Foreign Highway, 2010, 30(4):145-149.

[14]肖财,张开银, 黎晨. PC 弯曲孔道摩阻损失中接触应力分布试验[J]. 武汉理工大学学报(交通科学与工程版), 2015, 39(2):367-370. XIAO C, ZHANG K Y, LI C. Test of contact stress distribution in curving hole friction loss[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2015, 39(2):367-370.

[15]张文学, 谢全懿, 李学斌, 等. 高速铁路桥梁预应力孔道摩阻损失系数测试误差敏感性分析[J]. 中国铁道科学, 2015, 36(6):31-36. ZHANG W X, XIE Q Y, LI X B, et al.Analysis on test error sensitivity of prestressed duct friction loss coefficient of high speed railway bridge[J]. China Railway Science, 2015, 36(6):31-36.

[16]CHO K, KIM S T, PARK S Y, et al. Computation of the strand resistance using the core wire strain measurement[J]. Engineering, 2013, 5(11):850-855.

[17]JEON S, PARK S, KIM S T, et al. Estimation of friction coefficient using smart strand[J]. International Journal of Concrete Structures and Materials, 2015, 9(3):369-379.

Experimental study on channel friction resistance testof long span prestressed concrete beam bridge

ZHAO Kang, WEI Yang, DUAN Maojun, LI Guofen

(SchoolofCivilEngineering,NanjingForestryUniversity,Nanjing210037,China)

The friction in a post-tensioning system has a significant effect on the distribution of prestressing force in a prestressed concrete structure. One of the major causes leading to the deteriorations like the deflect ion and cracking of current long span prestressed concrete beam bridge was underestimating the prestressing loss. The failure or destruction of bridge structure was caused by excessive prestress loss. For more precise construction monitoring, combined with a three span continuous beam bridge, the actual frictional coefficient of the channel was obtained through field test. This paper made a contrast between friction coefficient of prestressing tendon at different lengths and pipeline deviation coefficient that measured, then modified finite element model with measured data. Finally, the comparison between modified theoretical calculation value and field measured value of support section roof stress was analyzed. The friction coefficients of prestressing tendons with different lengths were 0.254 and 0.282, respectively, and the deviation coefficientKwere 0.002 0 and 0.001 7, respectively. The results showed that the friction coefficient of the actual construction process was 1.6%-33.3% higher than the upper limit value of the norm, and friction coefficients of prestressing tendon at different lengths have obvious discreteness. Moreover, friction losses caused by normal extrusion force at the curve section increased with the increase in prestressing tendon length. Compared with the short prestressed tendons,μvalue of long prestressed tendons increased by 11%, andkvalue reduced by 15%. The changing trend of theoretical calculation values and measured values of roof stress was consistent. Errors decreased by 10% and 9% after parameter correcting based on measured values.

prestress; continuous beam bridge; friction resistance test; friction coefficient; construction monitoring

2016-01-14

2016-09-06

国家自然科学基金项目(51208262)；江苏省自然科学基金项目(BK20151520)；江苏高校优势学科建设工程资助项目(PAPD)；住房和城乡建设部科学技术项目(2011-K2-9)。

赵康，男，助理实验师，研究方向为预应力结构。E-mail:zkas_nfu@163.com

U443

A

2096-1359(2017)01-0143-06