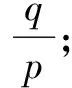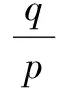关于整系数多项式有理根的几个定理及求解方法
张忠波
(江苏省徐州市铜山区铜山中学 221100)
相关定理的运用,可以最大限度地将有理根的范围缩小,从而进一步求出多项式的所有有理根,因此,定理的运用最大限速地简化了做题的思路.下面我们对有关定理以及求解方法进行一一论述.
一、整系数多项式有理根的相关定理


我们利用定理一可以得到以下定理:

3.定理三 设q是整系数多项式的整数根,那么q就是常数项a0的约数.因为定理都是经过长期的论证推断证明出来的正确的内容,因此这个定理在解题的过程中我们是可以直接运用的.
4.定理四 设整系数多项式f(x)=a0xn+an-1xn-1+…+a1x+a0的常数项a0是奇数,但是2p+q是偶数,那么p+q不是方程的有理根.
二、有理根的判定
关于整系数有理根的存在性问题我们通常的情况下可以把常数项的每一个因数分别代进多项式里面进行验证,但是当一个算式里面常数项非常大,因数的个数也比较多的时候,多项式的次数也相应的比较高,那么计算量会非常的大,单纯依靠我们人脑很难算出准确的答案,必须依靠计算机来进行帮助.但是,我们这是在直接计算的情况下,如果我们能首先判别多项式不可约,或者有些时候我们可以将一个多项式进行分解,如果这个多项式可以分解成好几个多项式的乘积.那么我们依靠人脑求出多项式的有理根在理论上是可行的,应该能求得的,但是问题又来了,将一个多项式分解为几个多项式的积并非一件容易的事情,在实际的操作过程中会有很大的困难.因此,研究多项式的有理根的问题,我们通常情况下从系数开始研究,首先判定是否存在有理根,下面是有理根的判别方法.
定理1 (Eisenstein判别法):设f(x)=anxn+an-1xn-1+…+a1x+a0在数学上为我们要求的式子.假设存在一个数p,使得
1.p+an;
2.p|an-1,an-2,…,a0;
3.p2+a0.
那么f(x)在有理数的定义域内是不存在约分情况的.
证明如果f(x)在有理数的定义域内是不存在约分情况,我们则可以根据2.2,f(x)在一定意义上讲将可以进行次数上的降低以及分解:
f(x)=(blxl+bl-1xl-1+…+b0)(cmxm+cm-1xm-1+…+c0)(l,m 因为p|a0,所以p能把b0或c0整除掉.但是p2+a0,所以p对于b0及c0而言不存在同时除掉的情况.在这种情况下我们应该假设p|b0但p+c0.另一方面,因为p+an,所以p|/bl.假设b0,b1,…,bl中首先不能被p整体除得的bk.通过对f(x)中xk的前面的常数进行分析,可以得到ak=bkc0+bk-1c1+…+b0ck.式中ak,bk-1,…,b0在某种意义上而言可以被p整体除得,所以bkc0在理论上也应该可以被p整体除得.可是p是我们数学上所言的素数,所以bk与c0中至少有一个被p整除.这在理论上是相互存在分歧的,是不统一的. (1)p+a0; (2)pm-1|an,但pm+an; (3) (i)当m≤n时,pm-k|an-k,k=1,2,…,m-1,且p|a1,a2,…,an-m; (ii)当sn≥m>(s-1)n+1时,其中s为正整数,pm-k|an-k,k=1,2,…,n-1 (注:当s=1时 ,与(i)相同) ,那么 ,多项式f(x)没有有理根 . 知f(x)=(sx-r)(b0xn-1+b1xn-2+...+bn-2x+bn-1)式中b0,b1,...,bn-2,bn-1都是整数,比较两边系数,即得 因为p是素数,且p|an,由(△)知p|rbn-1,所以p|r或p|bn-1,同时,因为p+a0=sb0,所以p+s且p+b0. 如果p|r,那么由p|an-m+1,及 (△)中sbn-m+1=an-m+1+rbn-m,所以p|sbn-m+1,即p|bn-m+1,故p2|rbn-m+1.又因为p2|an-m+2及sbn-m+2=an-m+2+rbn-m+2,所以p2|sbn-m+2,即p2|bn-m+2.又因为pm-1|an-1及sbn-1=an-1+rbn-2,所以pm-1|sbn-1,即pm-1|bn-1,所以pm|rbn-1=-an,故pm|an.与pm|/an矛盾.必有p+r,则p|bn-1. 由于p|an-1及由 (△)式中rbn-2=sbn-1-an-1,所以p|rbn-2,但p+r,必有p|bn-2. 由(△)式依次类推知p|b1. 由p|a1及sb1=a1+rb0,得p|rb0.又由前面所述知p+b0且p+r,p为素数.相互反驳,故f(x)是不存在有理根的. 由(ⅰ)证明知g(y)无有理根, 故f(x)无有理根. 通过上面的定理我们可以总结出求一个整系数多项式f(x)=anxn+an-1xn-1+…+a1x+a0存在有理根的方法: 第一步:首先判断f(x)在定义域范围内是否有有理根; 第二步:如果存在,求出an和a0的全部可能的因数; 整系数有理根的求法是人们常常讨论的数学问题,有着重要的地位,本文相对全面地介绍了整系数有理根的求法,希望可以对正在学习此内容的人有值得借鉴的地方,从而起到一定意义上的帮助作用,这是写作此文的目的所在. [1] 杨继明.关于整系数多项式有理根的求法[J].抚州师专学报,1994(3).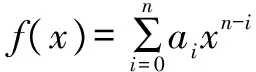
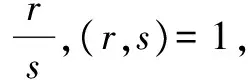

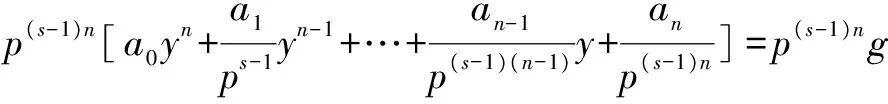
三、多项式有理根的求法