浅谈圆锥曲线离心率问题

潘 昊

(湖北省武汉市洪山高级中学高二(8)班 430074)

关于圆锥曲线离心率的文章在有关数学杂志中屡见不鲜.这主要是因为《中学数学新课程标准》对学生提出了更高的要求，也因此圆锥曲线离心率问题成为高考命题的热点之一.静下心来，翻开近几年的高考试题，有关圆锥曲线离心率的问题几乎年年考，各地考.在此我也将平时收集的这方面的文章和相关题目，整理成文，谈谈自己的一些见解和想法，仅供互相切磋学习.

一、直接利用公式或定义求离心率

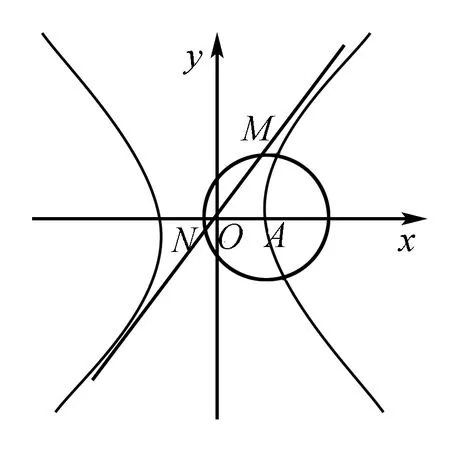
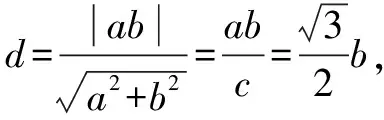
点评找出条件中能明确圆锥曲线中三个基本量a,b,c之间的等量关系，就可直接求解离心率e.

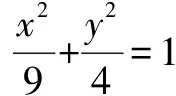
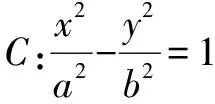
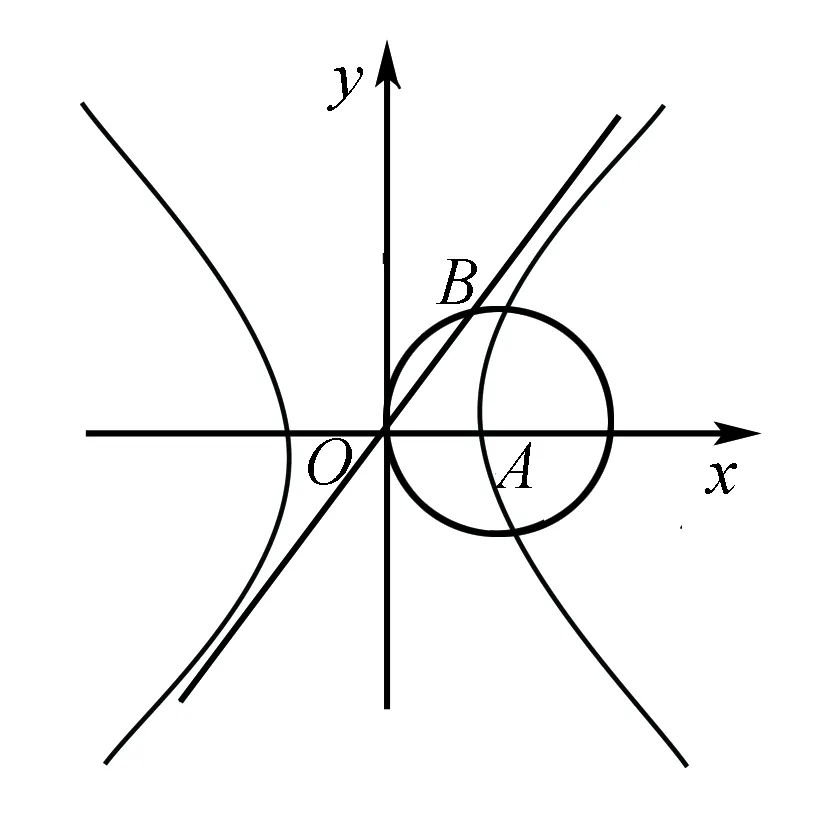
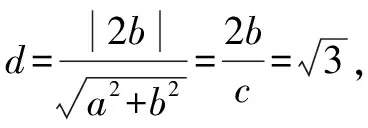
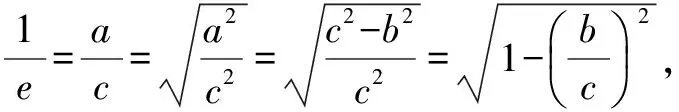
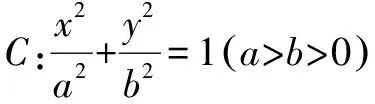
二、通过建立方程求离心率

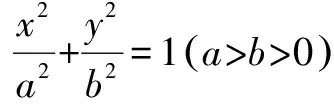
点评在求圆锥曲线的离心率时，若不能直接求出a,c的值，则应用椭圆中b2=a2-c2或双曲线中b2=c2-a2消去b，转化为关于a,c的齐次方程，进一步可转化为关于e的方程可解.这种建立方程求离心率e绝对是高考的重点之一，因而建立出方程成为关键.

练习3 (2015年全国Ⅱ)已知A,B为双曲线E的左，右顶点，点M在E上，△ABM为等腰三角形，且顶角为120°，则E的离心率为( ).

三、通过建立不等式界定离心率的范围

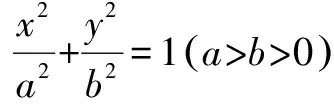
解由椭圆定义和余弦定理，

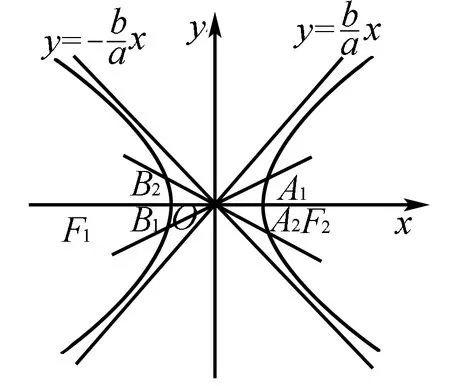
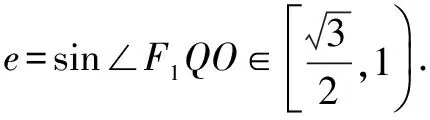
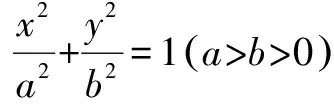
练习4 (2013年重庆)设双曲线C的中心为点O，若有且只有一对相交于点O，所成的角为60°的直线A1B1和A2B2,使|A1B1|=|A2B2|,其中A1,B1和A2,B2分别是这对直线与双曲线C的交点，则该双曲线的离心率的取值范围是( ).

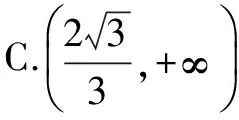
[1]吕华.例谈圆锥曲线离心率范围问题[J].学周刊,2011(26).

[2]米运芳.探求圆锥曲线离心率的取值问题[J].学周刊,2012(34).