初中数学课堂变式练习中如何去提升学科素养
黄 伟
(江苏省海门市悦来初级中学 226100)
在课改背景下的初中数学课堂教学基本上都采用“学生为主体,训练为主线,素养为主题”的原则.这种将提升学科素养作为教学的主题,无容置疑就必须使学生在数学学习中获得学科所涵盖的基础知识、基本技能,同时能掌握数学特色的思维方法,最终形成优良的数学思维品质.
一、课堂变式练习可以很好培养学生在同一题干下的发散思维
笔者多年的教育教学实践表明,变式练习有利于发展学生多层次、多角度发散的思维,不仅能让学生在问题的释疑过程中去积极寻找、分析类似问题的思路、方法,而且能够将教学过程中教师的“心智”“技巧”内化为学生的数学思维方法.通过实例就能清楚的看到变式练习的用武之地.如学习了一元二次方程和直角三角形的勾股定理之后,有这样的一个知识点可以作为数学思维训练.
例1 已知方程x2-14x+48=0的两根恰好就是Rt△ABC两条边的长,求Rt△ABC第三条边的长.

变式练习1 已知方程x2-14x+48=0的两根恰好就是Rt△ABC两条边的长,求Rt△ABC的斜边长.
变式练习2 已知方程x2-14x+48=0的两根恰好是Rt△ABC两条边的长,求Rt△ABC的最短边边长.
变式练习3 已知方程x2-14x+48=0的两根恰好是Rt△ABC两条边的长,求Rt△ABC的面积.
设计思想这样的数学变式练习,是在数学教学过程中对一元二次方程的概念、性质,直角三角形的定理、公式内涵的挖掘,并将问题从边长、周长、面积等不同角度、不同层次、不同情形、不同背景做出相应的变化,这种变式题只是保留了题干的条件而让形式发生变化,而其本质特征不变而解题推断发生变化.课堂中,多多设计这样的变式练习,不仅让学生深刻地理解知识,还有效地培养学生的数学思维能力,掌握一类数学问题的解题方法.
二、课堂变式练习可以很好培养学生在条件变化时的发散思维
在课堂上通过变式练习可以充分调动学生积极地投入到教学的全过程,有助于帮助学生建立独立分析和解决问题的思维方法,培养他们勇于探索、大胆创新的科学精神,从而自觉提升学生的数学学科素养.
例2 已知关于x的一元二次方程(1-m)x2-2x-1=0中,有两个不相等的实数根,求m的取值范围.
案例分析判断一元二次方程根的诸种问题中,必须要满足下列两个先决条件:一是二次项系数不为零;二是有不相等的实数根存在时,必须满足Δ=b2-4ac>0.
依据题意得1-m≠0且(-2)2-4(1-m)(-1)>0.解得m<2且m≠1.
变式练习1 关于x的一元二次方程(1-m)x2-2x-1=0有两个相等的实数根,求m的取值范围.
变式练习2 关于x的一元二次方程(1-m)x2-2x-1=0有两个实数根,求m的取值范围.
变式练习3 关于x的一元二次方程(1-m)x2-2x-1=0有实数根,求m的取值范围.
变式练习4 关于x的一元二次方程(1-m)x2-2x-1=0没有实数根,求m的取值范围.
设计思想这样的数学变式训练,是让学生掌握一元二次方程根的判别式的运用,能从真正意义上理解一元二次方程的根与其判别式的关系.为什么有这样的关系?要从解题中真正进行感悟.通过发散性的思维途径,让学生体验数学思维和创新的过程,从而在变式中增强对数学学习的兴趣和内驱力,不断提高自主探究的能力.
三、课堂变式练习可以很好培养学生在展示迁移中的发散思维
课堂的变式练习不是教师心血来潮、想当然的变换题型,其变化的关键需要以抓住问题的本质特征为前提,遵循学生认知发展规律,根据学情的适时而变.变式练习必须紧抓思维训练这条主线,巧妙的变换思维视角,多问、多思、多用等途径,帮助学生从不同途径构建分析释疑的有效方法.


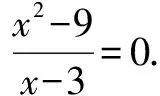
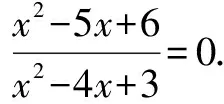
设计思想变式练习1作为分子x2-4=0时,x=±2,这时的分母2x-3≠0,不需要舍去什么值;变式练习2中的分子x2-9=0,得出x=±3,注意x=3时分母为0,因此要将x=3舍去,故满足条件的只有x=-3;同样地分析变式练习3,此时的分母可以因式分解为(x-3)(x-1)≠0,因此x的取值就不能等于3和1,作为分子x2-5x+6=0的两个解x=3和x=2,只能取x=2.通过上述的变式练习,学生就加深了对这一概念的理解,就能抓住概念的本质内容,也为教师在以后的课堂练习中明确类似知识点的出题方向,杜绝教师随意出题、学生盲目做题的不良现象,从而实现了课堂教学的高效性.
总之,习题训练采用“题海战术”是不可取的,因为题海不但消耗大量的时间,也容易消磨学生的学习意志.况且,数学中的经典习题数不胜数,即使是数学学霸也只能望题兴叹.尽管现代网络信息发达,练习题可以信手拈来,但解疑和释疑都会大大增加师生的额外负担,师生都没有充足的时间来完成这方面的工作.因此,在初中课堂上强化变式训练教学,完全可以让学生感悟至深,抓住数学练习中蕴含的知识点,快速提升学科素养.
[1]曹经伟.如何通过变式训练提高学生的数学素养[J].中学生数理化:教与学,2015(4).
[2]吴娜.初中数学有效教学策略探析[J].语数外学习:初中版上旬,2014(1):64-64.
[3]徐艳.中学数学思维能力提升的有效性摭谈[J].中学数学,2017(13):38-40.

