倾斜地球同步轨道卫星对北斗三频单历元基线解算的影响分析

徐梅,严超,乔方,苏迪

(安徽理工大学 测绘学院,安徽 淮南 232001)

0 引 言

北斗卫星导航系统(BDS)是中国着眼于国家安全和经济社会发展需要,自主建设、独立运行的卫星导航系统,是为全球用户提供全天候、全天时、高精度的定位、导航和授时服务的国家重要空间基础设施[1]。BDS的空间星座由对地静止轨道(GEO)卫星、倾斜地球同步轨道(IGSO)卫星和中高轨道(MEO)卫星三类卫星组成,且全部发射三频信号[2],与全球定位系统(GPS)、GLONASS和GALILEO相比,BDS增加了轨道高度较高、运动角速度较慢的GEO和IGSO卫星。截止2017年8月,北斗二代卫星在轨情况如表1所示。

由于GEO和IGSO卫星的高轨道特性,其可见性要远远优于MEO卫星,能大幅度增加观测时段内的卫星数,对增强区域导航性能非常有利[3]。文献[4]和[5]提出了附有约束的BDS单频单历元基线解算;文献[6]基于双频伪距和宽巷载波相位双差观测方程,实现BDS双频单历元基线解算;文献[7]和[11]按照固定难度从小到大依次固定超宽巷、宽巷和窄巷或基频模糊度,实现了BDS三频单历元基线解算。上述文献对于BDS单频、双频和三频基线解算做了较为深入的研究,但这些研究仅限于从整体上分析北斗混合星座对于模糊度固定和定位精度的影响,并未深入研究IGSO卫星的区域定位性能。对此,本文在已有的研究基础上,采用内蒙古地区和安徽地区的两条短基线,比较分析IGSO卫星对BDS三频单历元基线解算的影响。

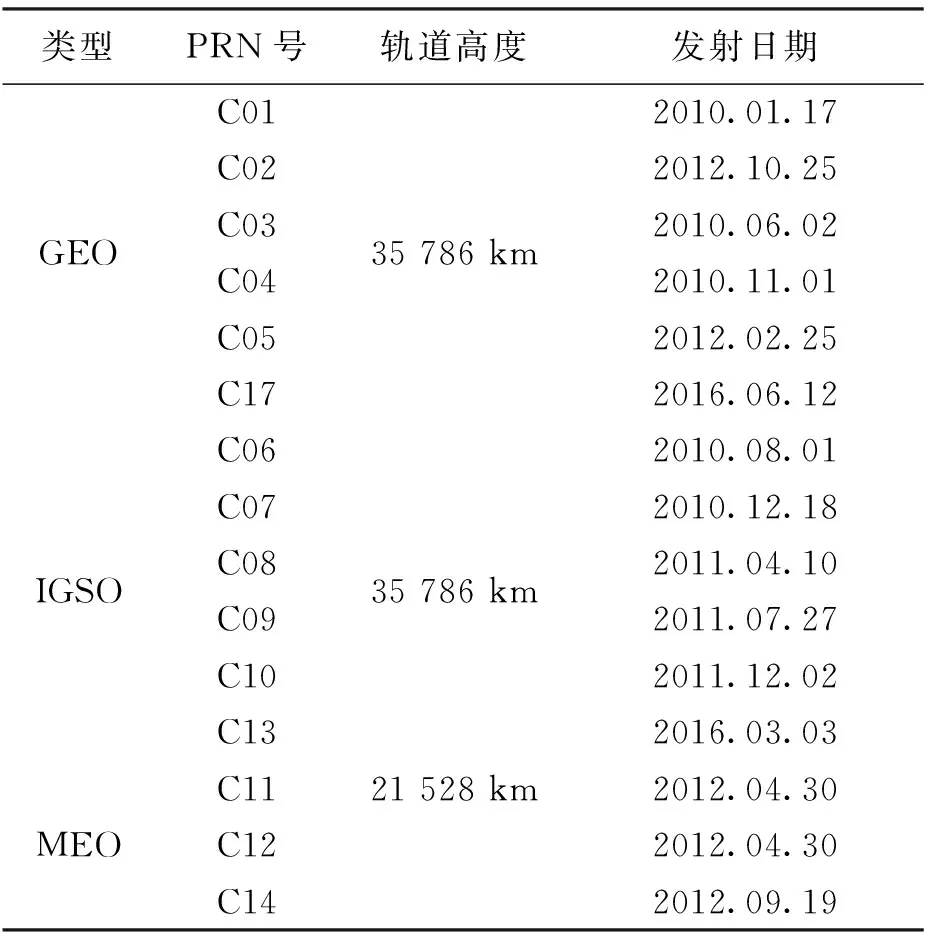
表1 北斗二代卫星在轨情况统计

联系人: 徐梅E-mail:xm1019aust@163.com

1 函数模型和随机模型

1.1 BDS三频单历元基线解算函数模型

三频情况下,频率的多样性可以提高无几何模糊度解算方法的可靠性[10]。BDS三频观测时,可以对载波观测值进行组合得到超宽巷(EWL)组合,根据文献[10]和文献[11],选择(0,-1,1)和(1,4,-5)两个超宽巷组合,EWL载波观测值与3个伪距观测值PB1,PB2以及PB3组成的基于几何模型的双差观测方程可表示为

(1)

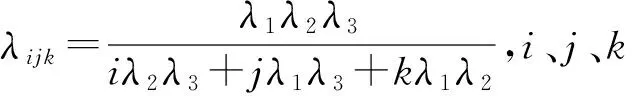
采用上述方法,可以成功固定(0,-1,1)和(1,4,-5)这两个WEL的ΔN(0,-1,1)和ΔN(1,4,-5)参数,将其看成高精度的距离观测值。由于短基线双差大气延迟误差较小,可以采用无电离层观测值消除电离层残差,因此可采用下式来求解BDS的基础模糊度:

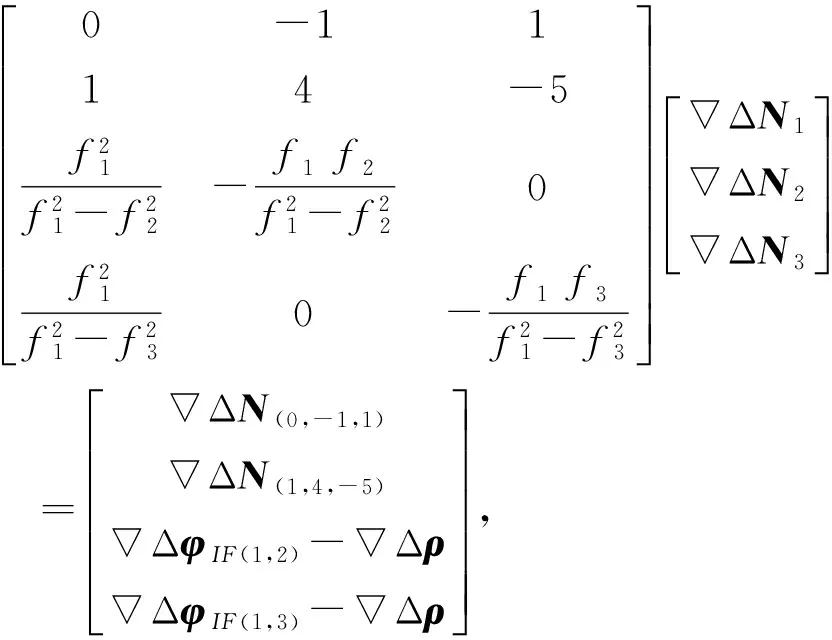
(2)

利用固定的BDS双差基础模糊度,求解参数X,即:

VB1=AX+(LB1+λ1ΔN1)

(3)

采用经典最小二乘估计得到参数X:

X=-(ATPA)-1(ATPL)

(4)

式中:P为权重;L=LB1+λ1ΔN1.

1.2 随机模型

BDS不同轨道卫星具有不同的性质,且不同频点信号质量之间具有差异,这是BDS单历元基线解算中不可忽略的问题。基于卫星高度角的随机模型[12]和基于信噪比的随机模型[13]在一定程度上能较为准确地反映观测值的观测质量,而因BDS不同轨道卫星高度不同的特点,也需考虑卫地距的影响。综上所述,所以可采用高度角、卫地距与信噪比组合模型进行定权[14]:

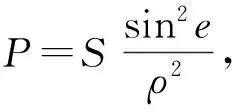
(5)

式中:S为缩放因子,S=

SNRB1、SNRB2、SNRB3分别为B1、B2、B3频点的信噪比值；ρ表示卫地距。

2 实验分析

本文选择了位于中国安徽省淮南和内蒙古自治区鄂尔多斯2个地区所观测的BDS三频短基线数据(<2 km)。其中,安徽淮南地区数据采样开始日期为GPS时2017年7月4日4时16分,取3600个历元数据,采样间隔1 s,基准站为JZJK,流动站为CS01;内蒙古自治区鄂尔多斯地区数据采样开始日期为GPS时2016年10月30日零时47分,取3600个历元数据,采样间隔1 s,基准站为JZTJ,流动站为CTJH。卫星截止高度角均设置为10°。

图1示出了观测时段内IGSO卫星信噪比随高度角的变化关系。表明观测时段内可见5颗IGSO卫星(两条基线均没观测到C13号卫星),但是可见性有所不同,这是因为5颗IGSO卫星均匀分布在3个倾斜同步轨道面上,其运动轨迹以赤道为对称轴的“8”字形,南北跨度较大,且每颗IGSO卫星覆盖范围限定于某一固定区域;IGSO卫星B1、B2、B3频点信噪比与高度角之间有一定的趋势性关系,即:卫星高度角越大,信噪比越大(CJTH站C08因为高度角变化较小,大约1°,所以规律性不明显)。

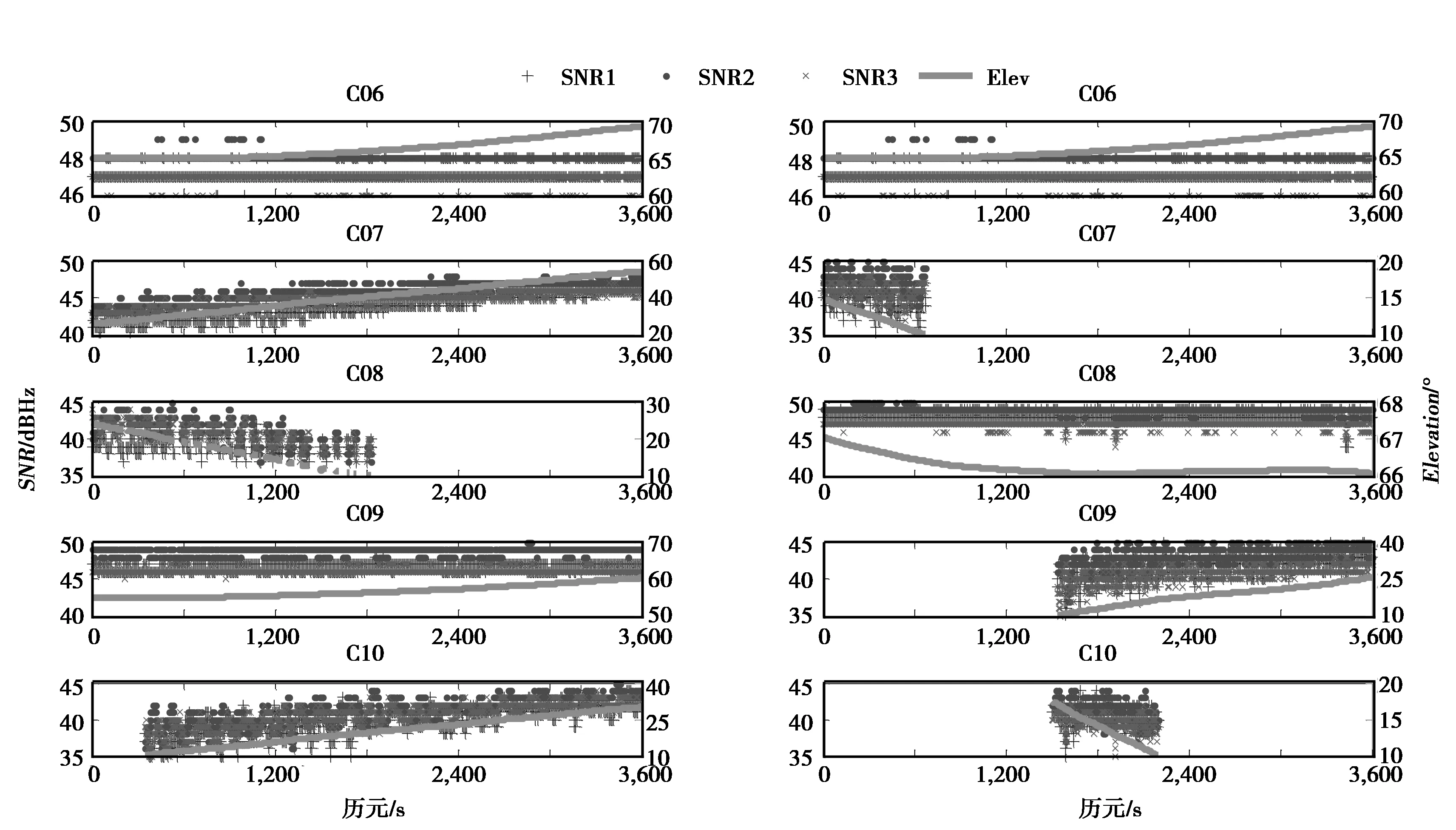
图1 流动站IGSO卫星信噪比随高度角的变化

根据IGSO卫星可见性,逐次增加一颗IGSO卫星,具体方案如下:

方案一:排除观测时段内所有的IGSO卫星,仅利用GEO和MEO卫星进行定位,参考卫星选用C03;

方案二:在方案一的基础上,两测区均增加C06;

方案三:在方案二的基础上,安徽测区增加C07,内蒙古测区增加C08;

方案四:在方案三的基础上,两测区均增加C09;

方案五:在方案四的基础上,安徽测区增加C10,内蒙古测区增加C07;

方案六:在方案五的基础上,安徽测区增加C08,内蒙古测区增加C10.

2.1 模糊度解算结果分析

对上述两条基线采用BDS三频单历元基线解算的数学模型进行单历元模糊度解算,解算结果的有效性检验可以用成功率进行衡量[15-16]。安徽测区基线以淮南矿业(集团)有限责任公司朱集东矿GNSS网数据处理结果作为参考值,内蒙古测区基线以淮南矿业(集团)有限责任公司唐家会煤矿GNSS网数据处理结果作为参考值。分别将各历元固定解与参考值进行比较,相同则认为是正确的。

成功率=正确固定历元数/有效历元数

两条基线采用不同方案模糊度解算的成功率如表2所示。

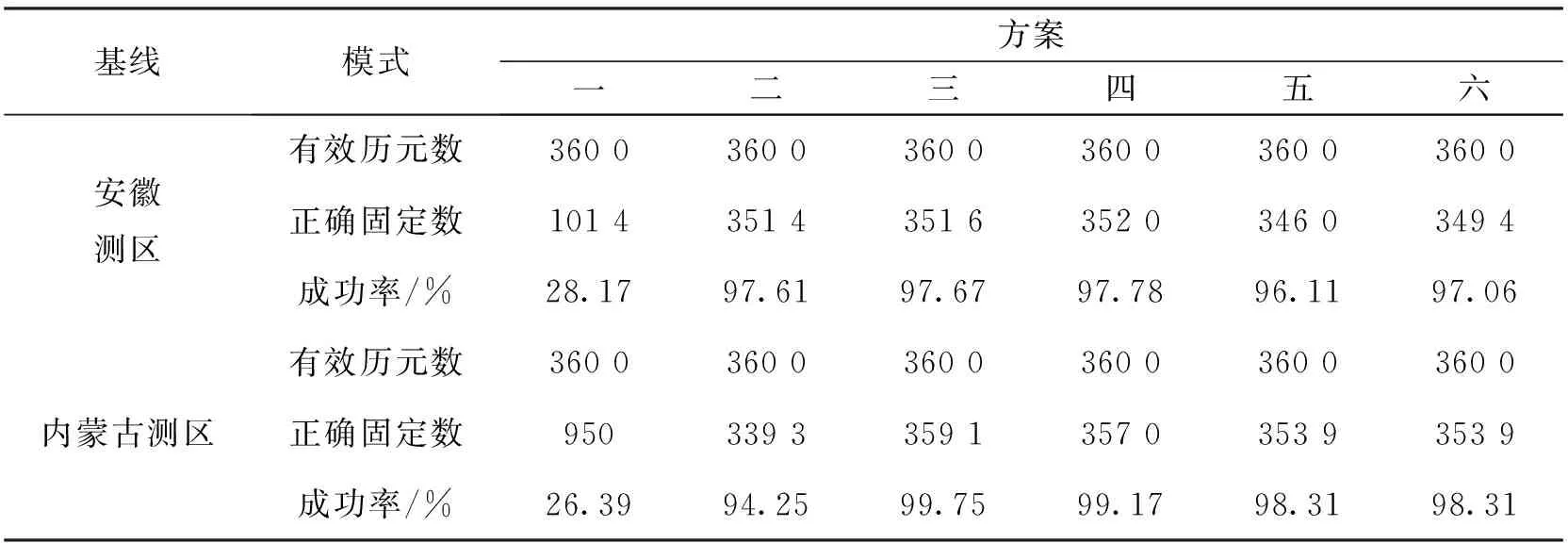
表2 不同方案下模糊度解算成功率统计

从表2可知:

1) 方案一中只存在GEO卫星的情况下(两测区在测段内均未接收到MEO卫星信号),仍能达定位要求,查看共视数据发现,在两测区的观测时段内均可接收到5颗GEO卫星,充分体现了GEO卫星作为地球静止轨道卫星对于中国区域的增强效果,但也说明只有GEO卫星参与解算时,BDS三频模糊度解算成功率较低,大约为30%;

2) 与方案一相比,方案二虽然只是增加了1颗IGSO卫星,但是成功率至少提升了246.5%,成功率高达90%以上,体现了IGSO卫星对于BDS三频模糊度解算成功率具有重要意义;

3) 由方案二、三、四、五、六可知,安徽测区增加3颗IGSO卫星模糊度解算成功率最高,内蒙古测区增加2颗IGSO卫星模糊度解算成功率最高,结合图1,这主要是两测区可见性最好的2～3颗IGSO卫星均参与计算,没有卫星升降对其解算结果造成影响;当增加4～5颗IGSO卫星时,模糊度解算成功率相对于2～3颗有所下降,这可能是引入了观测质量较差的IGSO卫星。

2.2 定位精度分析

本文在进行精度分析时,仅从定位结果角度出发,判断模糊度正确固定的历元的解算结果,与参考值作差,得到两条基线北(N)、东(E)、高程(U)三方向的定位结果,如图2、图3所示,并利用内符合精度(STD)进行精度分析,如表3所示。

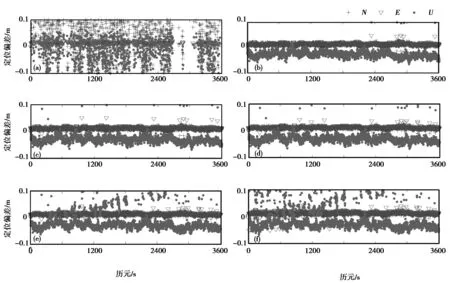
图2 安徽测区基线在N、E、U方向上的定位偏差 (a)方案一； (b)方案二； (c)方案三； (d)方案四；(e)方案五； (f)方案六

图3 内蒙古测区基线在N、E、U方向上的定位偏差 (a)方案一； (b)方案二； (c)方案三； (d)方案四；(e)方案五； (f)方案六

表3 内符合精度STD统计 单位：mm

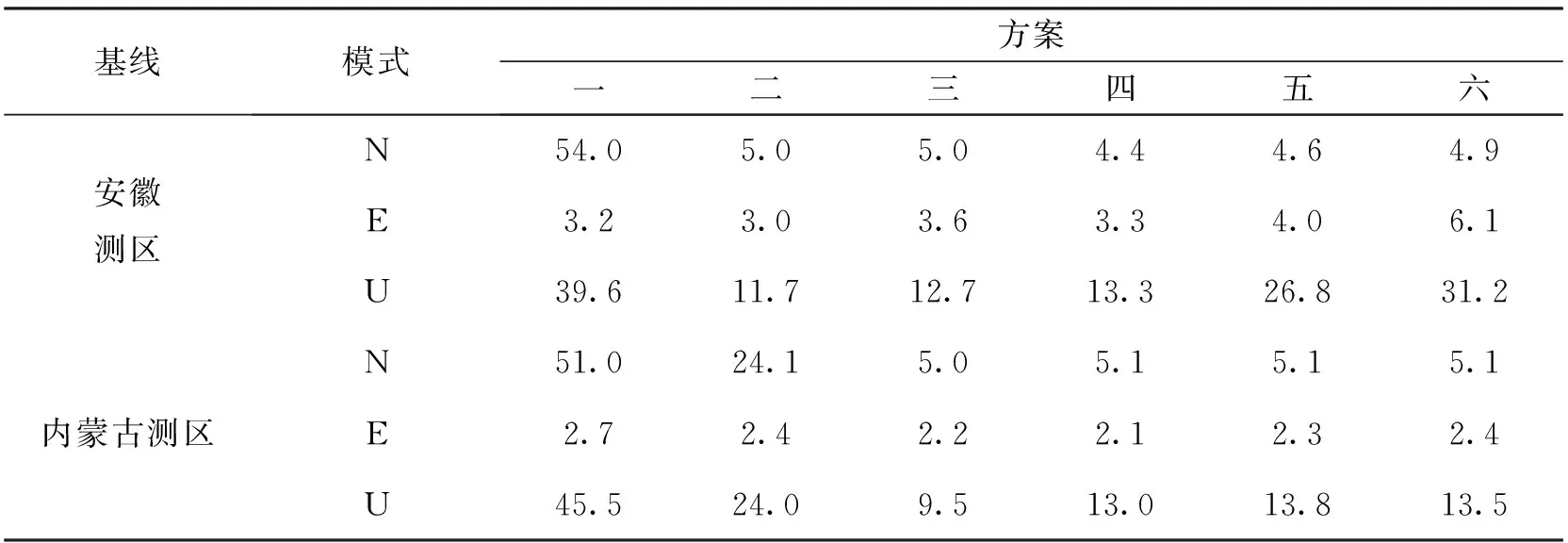
基线模式方案一二三四五六安徽测区N54.05.05.04.44.64.9E3.23.03.63.34.06.1U39.611.712.713.326.831.2内蒙古测区N51.024.15.05.15.15.1E2.72.42.22.12.32.4U45.524.09.513.013.813.5

结合图2、图3和表3可知:

1) 方案一中,N方向定位精度远远低于E方向,这是因为参与方案一解算的卫星为5颗GEO卫星,5颗GEO卫星分别定点于东经58.75°、80°、110.5°、140°和160°,而我国位于北半球;

2) 与方案一相比,方案二、三、四逐步增加一颗IGSO卫星,N、U方向定位误差相对于方案一均明显减少;在方案五、六中,增加两颗可见性较差的卫星时,N、E、U方向定位误差相对于方案三、四均有所降低,这是因为方案五、六中增加的两颗卫星高度角较低,且信噪比明显低于其他卫星;

3) 由方案二、三、四可知,分别增加1～3颗可见性较好的IGSO卫星时,N、E、U方向定位精度达到最佳;方案二、三、四、五、六中,U方向定位偏差基本偏向于同一侧,这可能是GEO卫星多路径效应引起的;解算结果N、E方向优于U方向,E方向优于N方向,误差分布与目前BDS服务性能一致。

3 结束语

与GPS相比,BDS的高轨道GEO卫星和IGSO卫星是其一大优势,除了其可见时段长、有利于增加用户的可见卫星数之外,高轨道卫星信号更容易被接收机接收,同时能有效减少低仰角卫星引入的多路径误差影响,尤其是在高楼建筑物阻挡的恶劣环境下,北斗系统特殊的星座构型能有效保证定位结果的稳定性。特别是IGSO卫星不仅具有GEO卫星的区域服务能力,还可以同时保证对高纬度地区的覆盖。本文利用我国内蒙古地区和安徽地区的实测数据,分析了IGSO对BDS三频单历元基线解算的影响。由数据分析可得:1) IGSO卫星B1、B2、B3频点信噪比随着高度角的增大而增大;2) 当只有GEO卫星参与定位时,BDS三频模糊度解算成功率低于30%,N、U方向定位误差较大,能达到5 cm左右;3) 按可见性逐次增加IGSO卫星参与定位时,增加1～3颗可见性较好的IGSO卫星时,模糊度解算成功率最高,且定位精度最佳;4)解算结果N、E方向优于U方向,E方向优于N方向,误差分布与目前BDS服务性能一致。

[1] 北斗卫星导航系统.北斗卫星导航系统介绍[EB/OL].(2010-01)[2017-05-23]. http://www.beidou.gov.cn/xtjs.html.

[2] 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1):1-6.

[3] 吴甜甜,张云,刘永明, 等. 北斗/GPS组合定位方法[J]. 遥感学报,2014, 18(5):1087-1097.

[4] 王静,赵兴旺,刘超.基于正则化的GPS/BDS单频单历元模糊度固定[J].大地测量与地球动力学,2016,36(12):1083-1087.

[5] 张书毕,刘鑫,宋冰,等. 附有约束的BDS单频单历元改进型Par Lambda算法[J]. 中国矿业大学学报, 2017(1):201-208.

[6] 唐卫明,邓辰龙,高丽峰. 北斗单历元基线解算算法研究及初步结果[J]. 武汉大学学报(信息科学版), 2013, 38(8):897-901.

[7] TANG W, DENG C, SHI C,etal. Triple-frequency carrier ambiguity resolution for Beidou navigation satellite system[J]. GPS Solutions, 2014, 18(3):335-344.

[8] 刘炎炎,叶世榕,江鹏,等. 基于北斗三频的短基线单历元模糊度固定[J]. 武汉大学学报(信息科学版), 2015, 40(2):209-213.

[9] 何俊,刘万科,张小红. 北斗短基线三频实测数据单历元模糊度固定[J]. 武汉大学学报(信息科学版), 2015, 40(3):361-365.

[10]谢建涛,郝金明,韩聪,等. BDS单历元TCAR算法优化研究[J]. 测绘科学技术学报, 2016, 33(1):6-10.

[11]吕伟才,高井祥,王坚,等. 北斗三频约束的短基线模糊度单历元算法[J]. 中国矿业大学学报, 2015, 44(6):1090-1096.

[12]RIZOS C. Principles and practice of GPS surveying[M].School of Geomatic Engineering, The University of New South Wales, Sney, 1997.

[13]LANGLEY R. GPS receiver system noise[J].GPS World, 1997(8):40-45.

[14]刘乾坤,隋立芬,肖国锐,等. 北斗系统差分码偏差解算中一种新的定权方法[J]. 测绘科学技术学报, 2015, 32(5):473-478.

[15]刘经南,邓辰龙,唐卫明. GNSS整周模糊度确认理论方法研究进展[J]. 武汉大学学报(信息科学版), 2014, 39(9):1009-1015.

[16]DENG C L, TANG W M. Reliable single-epoch ambiguity resolution for short baselines using GPS/BeiDou system[J]. GPS Solutions, 2014, 3(18):375-386.