GPS高程转换方法研究及精度分析
唐丽娟
(安徽理工大学 测绘学院,安徽 淮南 232001)
0 引 言
GPS定位技术由于其平面定位精度高、速度快而被广泛使用,GPS测量得到的三维坐标,实际上主要使用的还是其平面位置信息,而其高程信息并没有被充分利用。如何充分利用GPS观测值中提供的高程信息,直接为测绘生产服务,成为一项很有意义的工作。由于无法直接利用GPS测量高程代替水准高程,所以就必须将GPS大地高转换成正常高。
1 GPS高程拟合的原理
1.1 正常高和高程异常
我国高程系统普遍采用正常高系统,传统的水准测量获取结果是基于似大地水准面的正常高,而GPS测量得到的高程则是基于WGS-84参考椭球的大地高[1-2],如图1所示,若要使GPS测量的高程数据可以在实际的工程建设中使用,就必须进行高程系统的转换,这就需要知道这些测点的高程异常值。
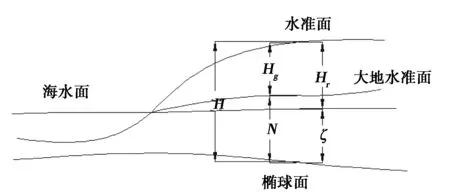
图1 参考基准关系图
H=Hg+N=Hr+ξ,
(1)
1.2 高程异常的求解
由式(1)可以得到:
Hr=H-ξ.
(2)
故只需知道高程异常ξ就可以确定该测点的正常高。目前,高程异常ξ获取的方法有从国家高程异常图上查取、利用地球重力场模型来确定高程异常值、从局部地区精化的大地水准面模型中获得。第一种方式获取的高程异常值的精度不高,一般都在分米级;第二种方式由于国家地球重力场模型保密,只能从全球地球重力场模型中得到,得到的高程异常值也只能反应大地水准面的基本变化趋势;第三种方法获得的高程异常值精度较高,虽然可以达到厘米级精度,但获取高程异常值的成本较高,一般难以承受[3]。
联系人: 唐丽娟E-mail: 764779713@qq.com;
由于上述方法都有其缺陷,应用GPS高程拟合的方法来得到高程异常的方法也就应运而生。GPS高程拟合即数值拟合方法,在测量过程中对若干个GPS控制点进行联测,根据有限的高程联测点把该区域的似大地水准面拟合为平面、多项式曲面或其他数学曲面,再根据拟合的曲面内插出区域内待定点的高程异常值,从而将待测GPS高程点的大地高转化成正常高。
2 GPS高程拟合模型
高程异常拟合的主要方法有多项式拟合、多面函数拟合法、BP神经网络法、Kriging插值法、分区拟合法等[4-8]。
2.1 多项式曲面拟合法
当GPS点分布在某一个区域时,使用曲面拟合法可以得到较好的效果。常用的曲面拟合模型有:
二次曲面模型:
ξ=a0+a1x+a2y+a3x2+a4y2+a5xy
(3)
三次曲面模型:
ξ=a0+a1x+a2y+a3x2+a4y2+a5xy+
a6x3+a7y3+a8y2+a9xy2
(4)
一般地,将以上数学模型按最小二乘原则,采用间接平差原理来求解未知参数。求得参数后,将待求GPS点的平面坐标带入模型,求得其高程异常,进而求得正常高。
2.2 多面函数拟合法
该方法认为在任意一个数学表面和任何不规则的圆滑表面,总可以使用一系列有规则的数学表面的总和,以任意的精度来逼近。该模型的一般表达式为
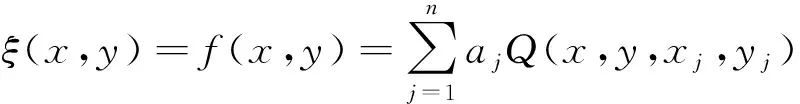
(5)
式中:aj为待定系数;Q(x,y,xj,yj)为核函数,高程异常可由二次式的和确定,故称为多面函数。核函数通常采用具有对称性的正双曲函数来表示,即:
Q(x,y,xj,yj)= [(x-xj)2+(y-yj)2+
δ]1/2,
(6)
式中,δ称为平滑因子,当待定点多于已知点时,任意点的高程异常表示为
ξ=Qp(QTQ)-1QTξ.
(7)
2.3 BP神经网络模型
BP神经网络又称为误差反向传播多层前馈神经网络,是研究得最多,应用最广泛的一种神经网络模型[9]。该模型由输入层、隐藏层和输出层组成,隐藏层可以是一层或者是多层,各个层由若干个节点(神经元)组成,同层间的神经元互不相连,前后两个层的神经元之间相互连接,前一层神经元输出的结果为后一层神经元的输入值[10]。如图2所示。
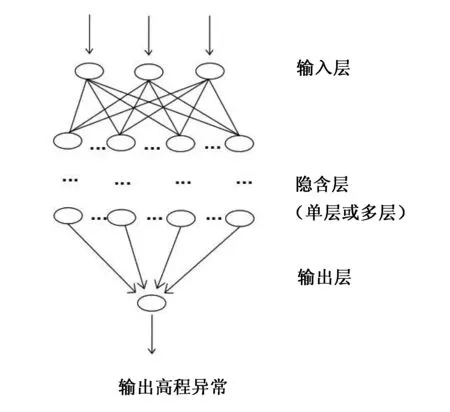
图2 BP神经网络结构图
当输入信号进入系统后,首先把信号传播到隐含层的神经元,经过一系列的计算后,再把隐含层神经元上的信号传播到输出层的神经元上。若输出层输出的结果得不到期望的值,就会逆向反馈传播,将有误差的信号按照原来的路径逐层返回,并通过不断修改各个神经元的权值,在达到误差信号变成最小时,输出结果。
3 实例分析
选取安徽省谢桥矿区2111(3)某工作面MSA倾向线为实验区域,测区东西长约1.4 km,南北长约0.4 km,测区面积约0.56 km2.在该区域内共布设65个GNSS/水准联测点,通过三等水准测量得到各点位的正常高,同时通过RTK获得各个点的GNSS大地高,测区点位分布总体呈线状分布且分布较为均匀,具体点位分布如图3所示,测区地形高程异常变化如图4所示。
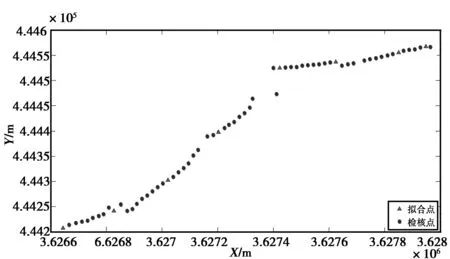
图3 测区点位分布图
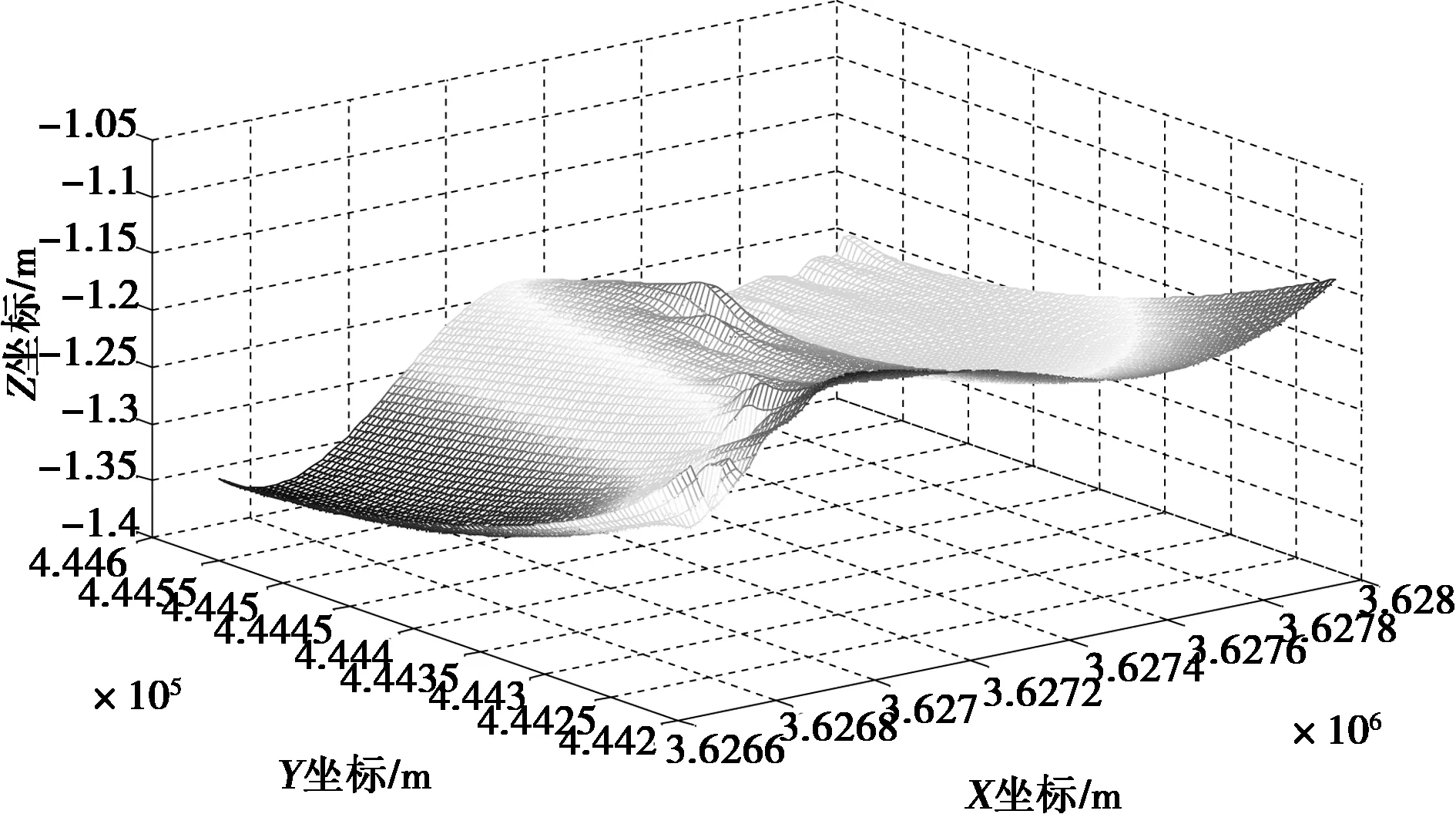
图4 测区高程异常变化情况
选取以图中红色实心三角形对应的MSA01、MSA10、MSA20、MSA30、MSA40、MSA50、MSA60、MSA65 8个拟合点作为高程拟合基准点,其余57个点作为检核点,分别使用平面、二次曲面、多面函数、BP神经网络拟合出剩余57个检核点的高程异常。经过计算得出各模型的内外符合精度、检核点残差统计情况如表1所示,检核点残差序列如图5所示。
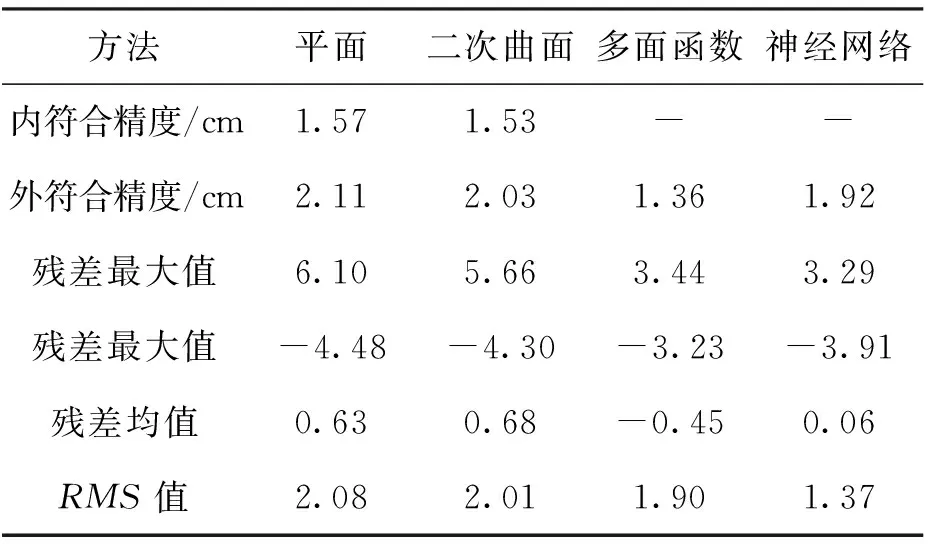
表1 各种高程转换方法结果对比
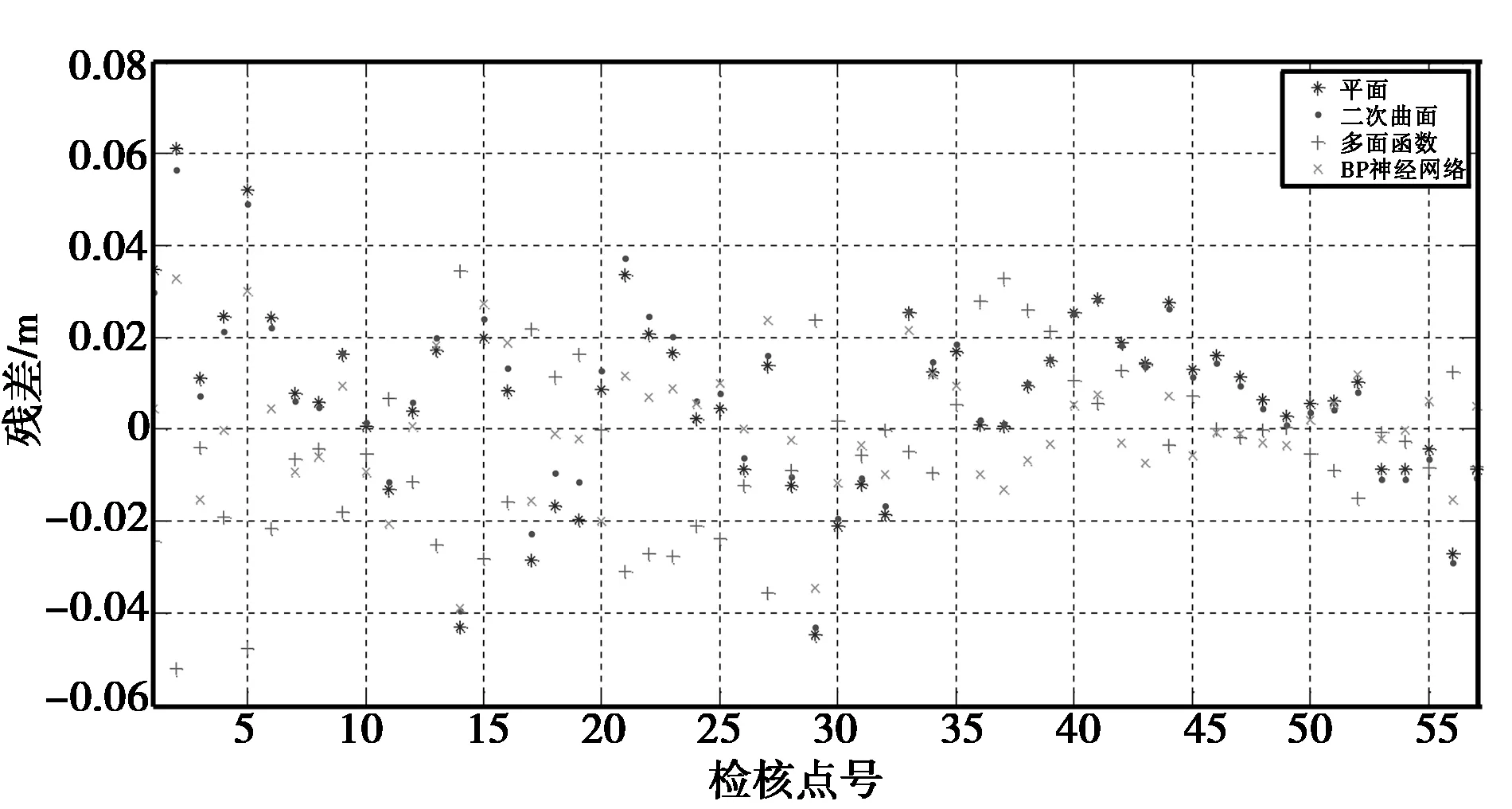
图5 高程异常残差图
从表1、图5可知,平面拟合检核点残差最大值为6.1 cm,最小值为-4.48 cm,均值为0.63 cm;二次曲面拟合检核点残差最大值为5.66 cm,最小值为-4.30 cm,均值为0.68 cm;多面函数拟合检核点残差最大值为3.44 cm,最小值为-3.23 cm,均值为-0.45 cm;BP神经网络拟合检核点残差最大值为3.29 cm,最小值为-3.91 cm,均值为-0.06 cm;多面函数的外符合精度最高,平面拟合的外符合精度最低,平面拟合精度与二次曲面拟合精度基本一致。其中,多面函数相比二曲面拟合外符合及精度高出7~8 mm,残差最大值与二次曲面拟合减小了2.22 cm,残差最小值比平面拟合减小了1.07 cm,与BP神经网络相当。BP神经网络的RMS值最小为1.37 cm,平面函数与二次曲面的RMS最高都在2.00 cm左右,多面函数的RMS值为1.90 cm.
此外,由于本实验测区范围较小,所以几种拟合方法的效果差异并不太显著,就小范围的测区而言,BP神经网络与多面函数的拟合效果最好,但由于BP并不是一个纯粹的数学模型,故在实际使用中应优先多面函数法进行高程转换。
4 结束语
本文采用平面拟合、二次曲面拟合、多面函数、BP神经网络4种方法对实验区域进行了GPS高程转换研究,其中多面函数与BP神经网络高程拟合的精度最佳,其拟合残差在1~3.5 cm之间,BP神经网络的RMS值达1.37 cm,多面函数拟合的RMS值达1.90 cm,基本可以满足一般工程建设的要求。同时,说明利用GPS测量结合水准测量的数据来拟合高程异常值,进而计算出各GPS点的正常高,是一种行之有效的方法,在小区域地势平坦的范围内更加有效。
[1] 高彩云,臧德彦,高宁.GPS高程拟合系统的研究[J].江西测绘,2006:46-48.
[2] 余宣兴,詹昊,朱明新,等.EGM2008地球重力场模型在GPS高程转换中的应用研究[J].测绘通报,2013,(12):18-20.
[3] 吴恒友.基于EGM2008重力场模型的GPS高程拟合测量的实用性分析[J].大地测量与地球动力学,2015,12(6):945-952.
[4] 张正禄,李广云,潘国荣,等.工程测量学[M],武汉:武汉:武汉大学出版社,2013.
[5] 徐绍铨,张海华,杨志强,等.GPS测量原理与应用[M].武汉:武汉大学出版社,2003.
[6] 余学祥,王坚,刘邵堂,等.GPS测量与数据处理[M].徐州:中国矿业大学出版社,2013.
[7] 陈艳红,马全明,刘瑞敏,等.基于相对高程异常的GPS高程拟合方法探讨[J].测绘通报,2014(12):67-69.
[8] 王承华,马洪滨,董仲宇.GPS水准多项式曲面拟合模型的优选实验研究[J].矿山测量,2007(1):35-37.
[9] 胡川.基于神经网络的GPS高程拟合及其MATLAB实现[J].城市勘测,2010(5):75-77.
[10]牛志宏.几种基于神经网络的GPS高程拟合方法比较[J].测绘,2014,39(2):64-67.
——以大班艺术领域为例

