GPS/BDS/GALILEO多系统融合伪距单点定位性能分析

贾雪,徐炜

(安徽理工大学 测绘学院,安徽 淮南 232001)

0 引 言

目前,我国的BDS系统已实现对亚太周边地区的覆盖,并按照“三步走”的发展战略,计划2020年完成35颗卫星发射组网,为全球用户提供服务[1]。同时,欧盟的GALILEO系统也正处于建设阶段,截止2017年8月可观测卫星数约在14颗左右,已初步具备定位能力,伴随着GPS现代化的实施,GPS单点定位的能力也逐步提高,定位精度达到1～5 m,在轨卫星共31颗[2]。

在单点定位时,定位精度受可见卫星数目的影响较大,在有建筑物或树木的遮挡区域,单系统的可见卫星数目大大减少,导致单系统定位无法获得可靠的定位结果,多系统的融合定位可以增加可见卫星的数量、改善卫星的空间几何构型强度、提高定位的精度[3]。国内外学者对BDS、GPS多系统融合定位的研究较多,而对BDS、GPS、GALILEO三系统组合定位的研究却较少。

鉴于此,本文在截止高度角10°、15°、20°、30°、40°的情况下,进行了GPS、BDS、GPS/BDS、GPS/GALILEO、BDS/GALILEO、GPS/BDS/GALILEO 6种模式伪距单点定位解算,并对其定位精度进行了比较。

1 GPS、BDS、GAILIEO单点定位模型

1.1 时间系统与坐标系统的统一

GPS采用GPS时(GPS time,GPST)和WGS-84坐标系(World Geodetic System 1984,WGS-84),BDS采用BDS时(BDS time,BDST)和CGCS 2000大地坐标系(China Geodetic Coordinate System 2000,CGCS2000),GALILEO采用GST时(Galileo System Time,GST)和GTRF坐标系(Galileo Terrestrial Reference Frame,GTRF),GPS、BDS、GALILEO的时间基准与坐标基础都存在差异,因此在进行组合定位时需要将两者的时间系统与坐标系统进行转换和统一起来[4-6]。

联系人: 贾雪 E-mail: 978256064@qq.com;

BDS与GPS系统均采用原子时,秒长的定义相同,也都采用周和周内秒数进行计数,不同在于GPST的起始时间为1980年1月6日的0时0分0秒的协调世界时(UTC),而BDST的起始时间是2006年1月1日0时0分0秒的UTC,GPS、BDS时间系统关系如图1所示。

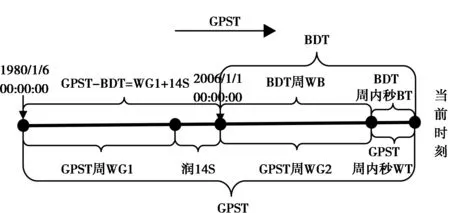
图1 GPST与BDT转换关系图

GPST与BDST的转换关系可以表示为

BDST周数=GPST周数+1356,

BDST周内秒数=GPST周内秒数+14.

但在GPST周内秒数+14大于604800时需要将BDST周数加1。

GALILEO采用的GST时间系统与国际原子钟时间(TAI)同步,标准误差为33 ns,GPST与GST的转换公式为:

GPST=GST-19S±30 ns.

WGS-84坐标系与CGCS2000坐标系的所定义的大地原点、尺度、定向是相同的,参考椭球面参数也较为相近,唯有扁率有微小的差异。WGS-84坐标系经过优化后的精度可达到2 cm,与ITRF精度基本一致,而CGCS2000与ITRF的差异大约在5 cm,所以,WGS-84与CGCS2000存在cm级别的差异;而GTRF与WGS-84坐标系统的差异非常小,一般为1～2 cm,在进行非精密测量时可将三个坐标系间的差异忽略不计,不需要进行坐标系统间的转换[7-8]。对于伪距单点定位而言,由于其定位精度在米级,因此无需进行坐标系统之间的转换,直接将其视为统一坐标系统使用即可[9]。

1.2 单点定位模型

GPS、BDS、GALILEO伪距观测方程可以统一表示为

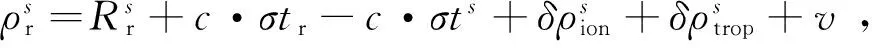
(1)式中: 设接收机的坐标为(XrYr,Zr);(Xs,Ys,Zs)

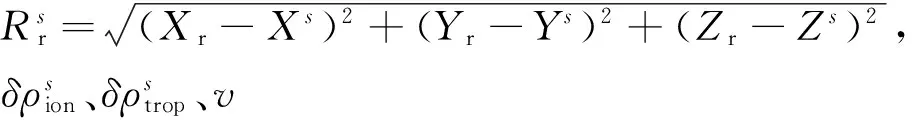
V=AδX-L，

(2)

式中:

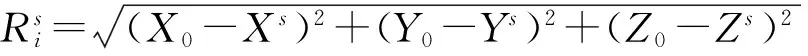
δX=(ATPA)-1ATPL.

(3)

单系统单点定位的未知参数有3个坐标分量和1个接收机钟差,双系统融合单点定位的未知参数有3个坐标分量和2个接收机钟差,三系统融合单点定位的未知参数有3个坐标分量和3个接收机钟差。因此,单系统单点定位时至少需要同时观测到4颗卫星,双系统组合单点定位时至少需要同时观测到5颗卫星,三系统组合单点定位时至少需要同时观测到6颗卫星[10]。在多系统融合计算时不同系统间视为等权,同系统间使用高度角定权,多系统融合伪距单点定位流程如图2所示。

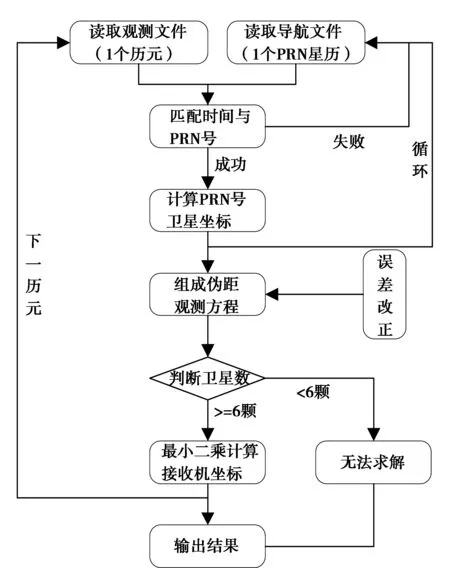
图2 多系统融合伪距单点定位流程图

1.3 主要误差项的处理

在单点定位中,除了电离层延迟、对流层延迟、多路径效应、接收机钟差、卫星钟差外,还有相对论效应、卫星轨道误差、天线相位中心误差、地球旋转误差等。本文对各个误差项的改正为:对于电离层延迟,采用Klobuchar模型进行改正,对流层延迟采用Saastamoinen模型改正,卫星钟差的改正模型为:δt=a0+a1(t-t0)+a2(t-t0)2,其中t为卫星钟观测时刻,t0为参考时刻,a0、a1、a2可以由

广播星历得到。相对论效应的改正模型为

由于地球自转对卫星坐标进行的改正为

2 实验数据处理与分析

2.1 GPS/BDS/GALILEO单点定位性能分析

本实验采用香港连续运行参考站HKMW站点采集的数据,观测时间为2017年8月12日0时0分0秒至2017年8月13日0时0分0秒,数据采样间隔为30 s。

分别对GPS(G)、BDS(C)、BGS+GALILEO(CE)组合、GPS+GALILEO(GE)组合、GPS+BDS(GC)组合、GPS+BDS+GALILEO(GCE)组合进行伪距单点定位,由于GAILIEO系统在某些时刻的可见卫星数少于4颗,故不对GALILEO单系统进行单点定位分析。设置卫星截止高度角为10°,对比各种定位模式的可见卫星数,PDOP值,并将以ORS站网解算出的HKMW站点参考坐标与与计算结果进行求差,得出X、Y、Z三个坐标分量的偏差及RMS值。可见卫星数、PDOP值、X、Y、Z坐标偏差变化如图3所示。

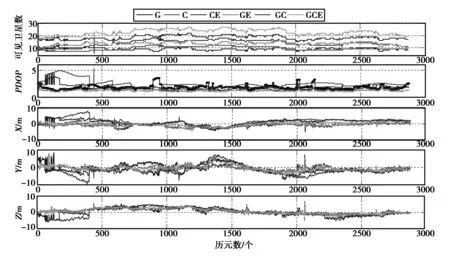
图3 测站的可见卫星数、PDOP值及X、Y、Z方向的偏差

从图3可以看出,BDS系统的稳定性比GPS系统的稳定性低,GPS/BDS/GALILEO组合系统的稳定性最好。BDS的PDOP值高于GPS,GPS的PDOP值高于BDS/GPS组合定位的PDOP值,这说明虽然BDS已经能够实现对亚太地区的覆盖,但还未实现对全球的组网,卫星的空间分布较GPS稍差,而GPS/BDS/GALILEO的组合定位使得位可见的卫星个数增加了2倍,大大增加了导航卫星的个数,提高了空间几何构型的强度,使得定位的PDOP值得到了降低。而由于GALILEO正在处于建设阶段,可观测定位卫星数量较少,因此相对于BDS/GPS的组合,GPS/BDS/GALILEO的组合对定位精度的提升并不明显。

利用这6种方法解算出的HKMW测站三维坐标分量的RMS值、全天平均PDOP值、平均可见卫星数量如表1所示。

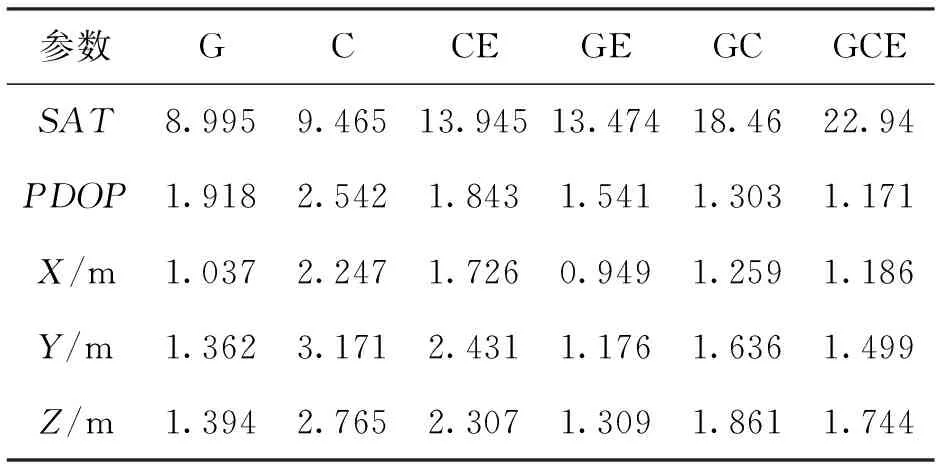
表1 站点平均可见卫星数、PDOP值及坐标分量的RMS值

从图3及表1可得出,BDS的可见卫星数比GPS的可见卫星数较多,得益于BDS的GEO卫星与IGSO卫星的作用,但单BDS比单GPS的PDOP值、三维坐标的偏差却要大。

GPS/BDS/GALILEO组合定位的可见卫星数相对于单GPS、BDS系统提升了255.03%、243.66%,PDOP值减小了38.94%、53.93%.其中,在X方向,BDS/GPS/GALILEO组合解算相对单GPS系统减小了13.1%,相对BDS系统提高了47.2%,这是由于组合定位虽然增加了可见卫星数,但由于BDS伪距的误差相对较大,造成定位精度的减弱;在Y方向,BDS/GPS/GALILEO组合解算相对单GPS系统减小了10.0%,相对BDS系统提高了52.7%;在Z方向,BDS/GPS/GALILEO组合解算相对单GPS系统减小了25.1%,相对BDS系统提高了36.9%.

GPS/GALILEO组合定位的三维坐标偏差最小,相对BDS/GALILEO组合的坐标偏差分别减小了0.777 m、1.255 m、0.998 m,相对BDS/GALILEO组合的坐标偏差分别减小了0.237 m、0.323 m、0.435 m,其主要原因在于BDS GEO卫星轨道和钟差精度偏低,从而导致了定位精度较差。

2.2 不同截止卫星高度角度单点定位性能分析

为了验证多系统组合在不同高度角情况下的单点定位性能,分别设置截止卫星高度角为15°、20°、30°、40°,不同截止卫星高度角的可见卫星数、PDOP值变化如图4～图6所示。

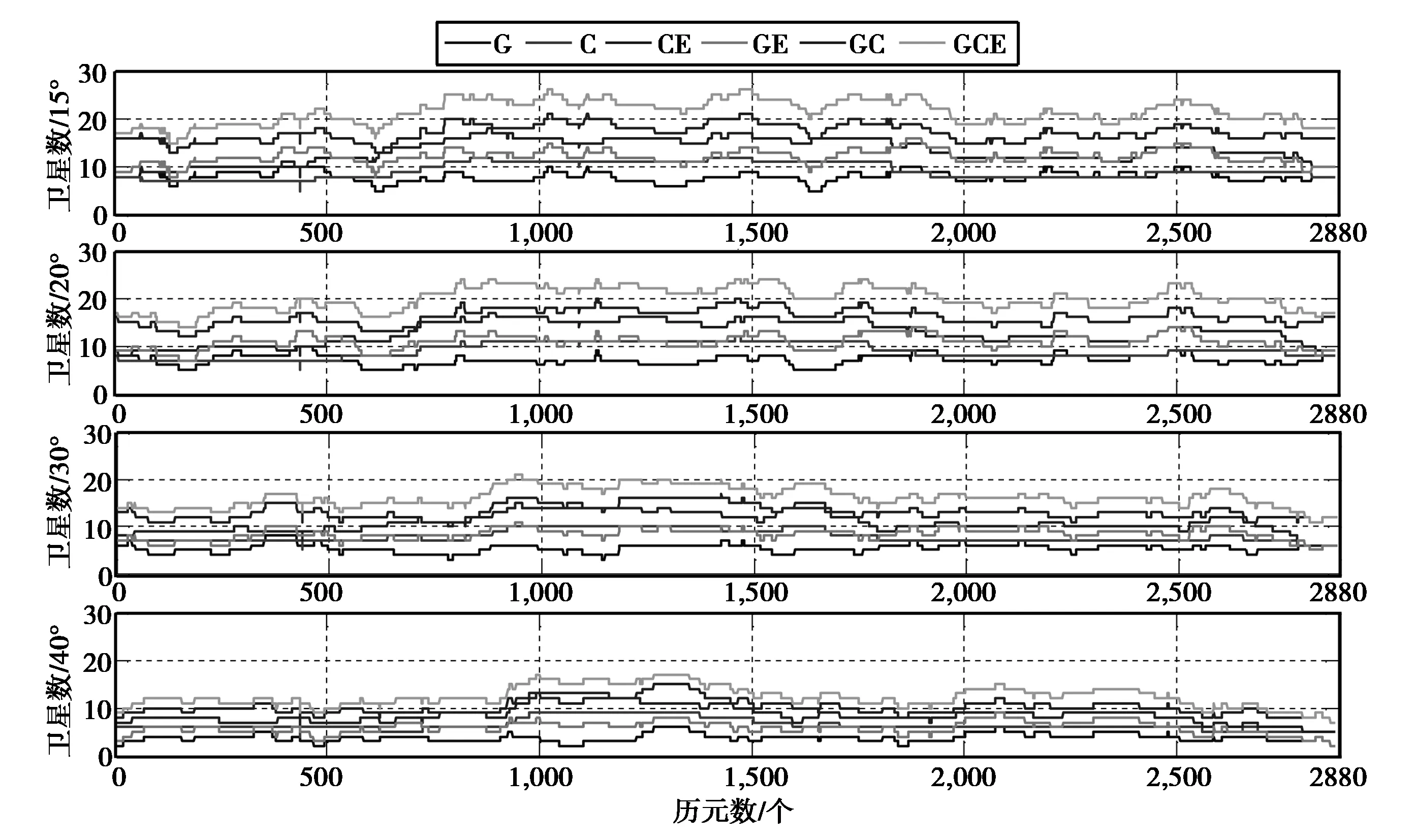
图4 不同截止卫星高度角可见卫星数目变化

图5 不同截止卫星高度角PDOP变化图

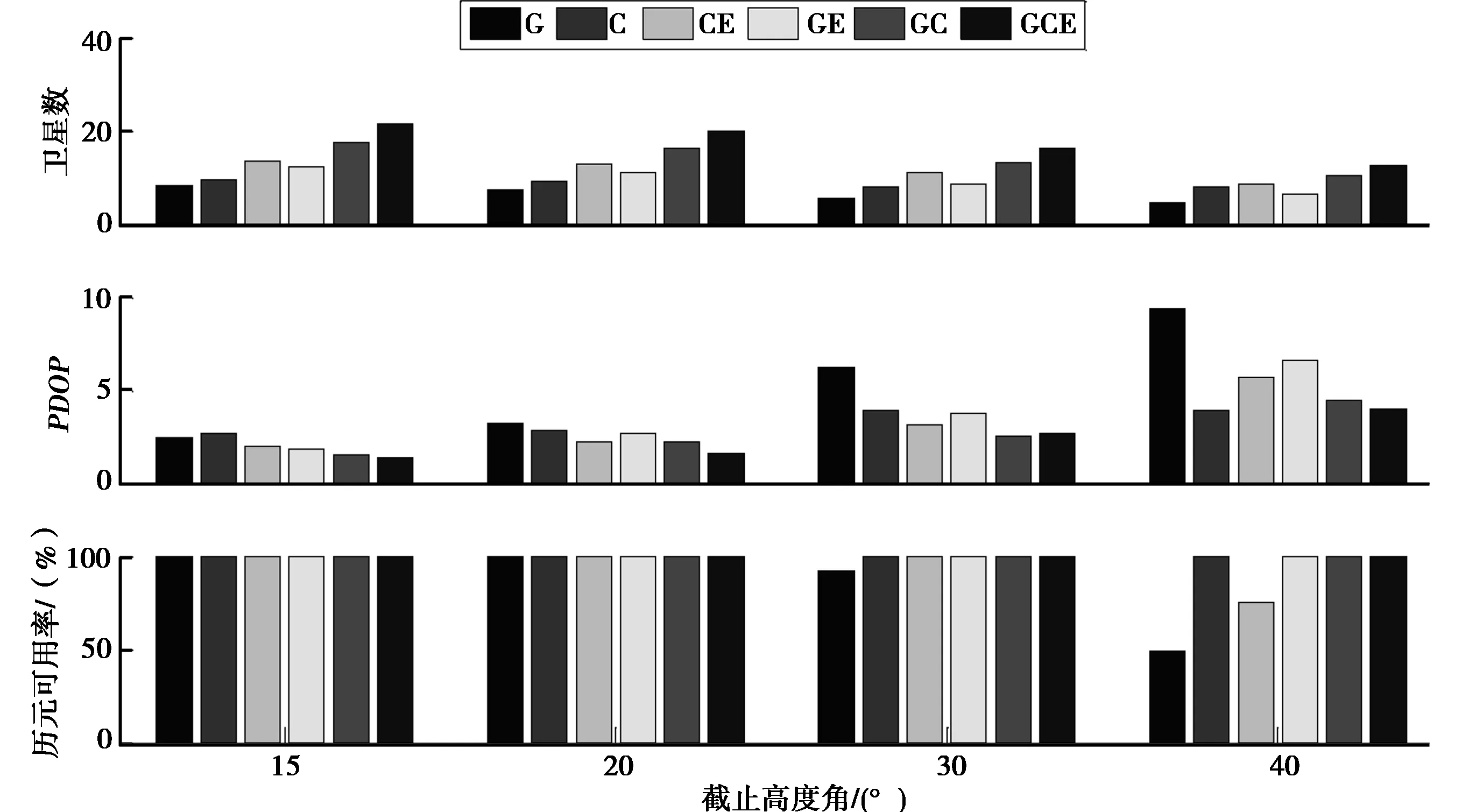
图6 平均可见卫星数、PDOP值、历元可用度随高度角变化情况

由图4、图6可知,在截止卫星高度角为15°、20°、30°、40°的情况下,HKMW站GCE组合的平均可见卫星数分别为21.45、19.91、16.20、12.33颗,GGA组合的平均卫星数为12.183、10.985、8.36、6.45颗,BGA组合的平均可见卫星数为13.42、12.825、10.85、10.58颗,单GPS系统的可见卫星数为8.036、7.136、5.46、4.41颗,单BDS系统的可见卫星数为9.242、9.01、7.854、7.84颗,组合系统的可见卫星数始终远远多于单系统,其中GBGA组合在截止高度角为40°时的可见卫星数比单GPS、BDS系统在高度角为15°时的可见卫星数还多3～4颗。在截止高度角为30°时,GPS系统的可用历元为92.066%,截止高度角为40°时,GPS系统的可用度为48.816%,而BDS系统由于GEO与IGSO的作用,历元的可用度一直为100%,对于CE、GE、GC、GCE各组合系统而言,仍然可以完全实现定位。

由图4、图6可知,在截止高度角15°、20°、30°、40°的情况下,GPS单系统的PDOP值分别为2.41、3.17、6.22、9.37,BDS单系统的PDOP值为2.67、2.79、3.88、6.61,BGA组合的PDOP值为1.98、2.17、3.09、5.63,GGA组合的PDOP值为1.82、2.67、3.75、6.61,GBGA组合的PDOP值为1.34、1.54、2.62、3.96,对于各组合系统、GPS单系统、BDS单系统,PDOP值与卫星截止高度角成正比,同一观测时段BDS的PDOP值均比GPS高,因此,虽然BDS的可见卫星数目大于GPS系统,但是卫星的空间几何构型强度比GPS系统差;在卫星高度角为40°时,GCE组合在HKMW站的PDOP值变化较为平稳,基本维持在4.0左右,说明组合系统伪距单点定位的几何图形得到了增强,定位精度得到了提高。

全天全观测时段内,在15°、20°、30°、40°截止卫星高度角下GPS、BDS、BDS/GALILEO、GPS/GALILEO、GPS/BDS/GALILEOX、Y、Z方向的定位偏差位如图7所示。

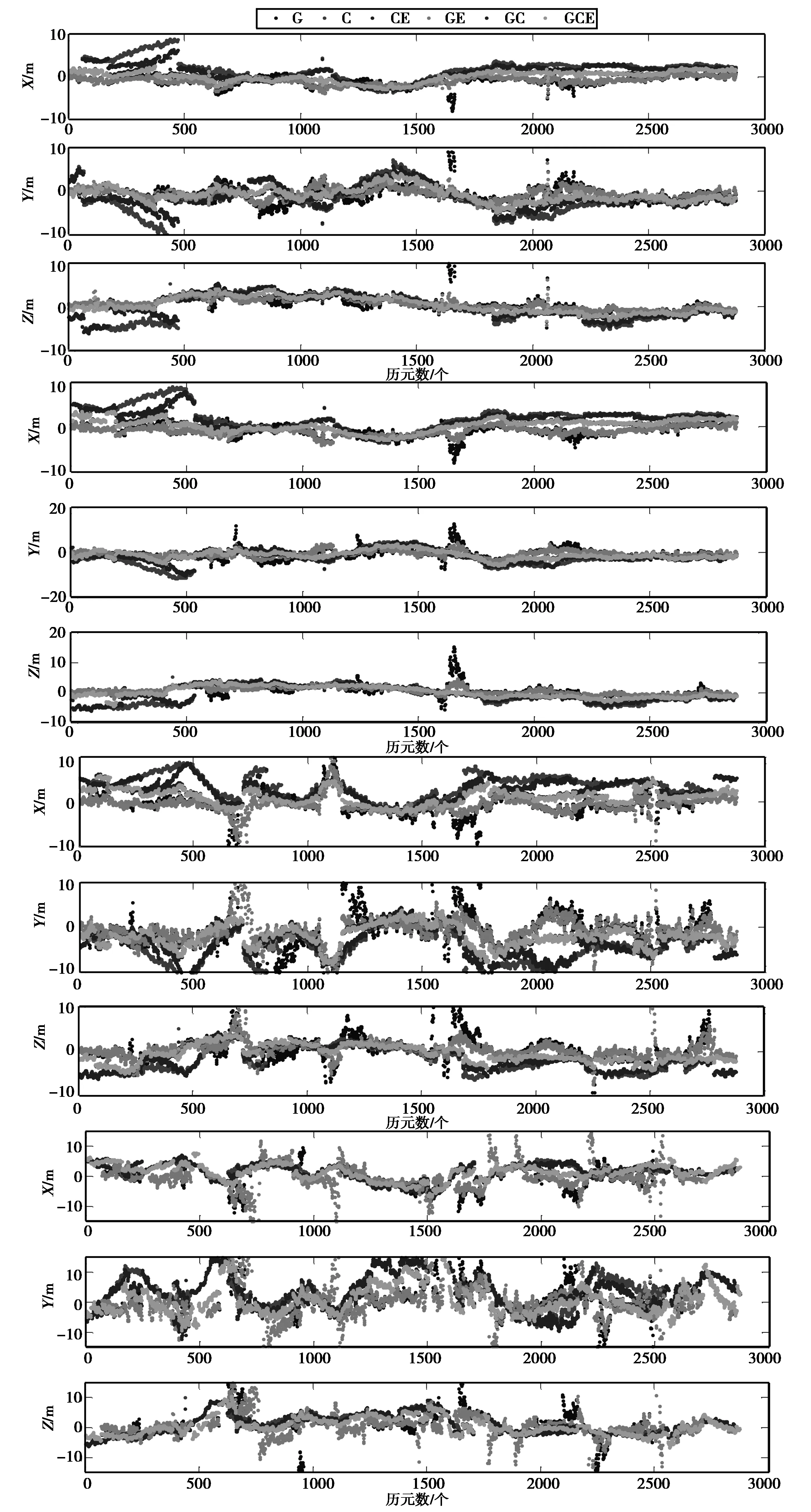
图7 从上到下15°、20°、30°、40°时卫星高度角三维坐标偏差

由图7可知,在不同截止卫星高度角情况下,GCE组合定位的稳定性都最高,在截止高度角为15°、20°时,由于GPS卫星的可见卫星受到的影响较小,而BDS 因其GEO卫星轨道和钟差精度偏低,故GPS单系统的定位精度优于BDS单系统,GE组合的定位精度最高,其RMS值与单GPS系统和GCE组合定位的RMS值基本相当。当截止卫星高度角为30°时,GPS单系统的历元可用度为90%,此时GPS与BDS系统的定位精度相当,而当截止卫星高度角为40°时,GPS单系统的历元可用度为48.816%,可见卫星数目下降,GPS系统在X、Y、Z方向的RMS值比BDS系统的都要大,GE组合定位的RMS值也随之下降,此时GCE组合仍能实现定位,说明了组合定位的优势。

3 结束语

随着我国BDS系统面向全球的组网、以及GALILIEO系统的建设,本文通过香港HKMW全天的实测数据,对GPS、BDS、BGS/GALILEO、GPS/GALILEO、GPS/BDS/GALILEO在不同截止卫星高度角下的定位结果进行了分析,得出以下几点结论:

1) BDS单点定位的精度已经能达到米级,但BDS系统的定位精度仍稍逊于GPS系统,GPS/BDS/GALIEO组合系统的稳定性最好,在X、Y、Z方向的定位精度都优于单系统。

2) GPS/BDS/GALILEO组合系统比单系统单点定位可以观测到更多的可见卫星,提高了系统的可靠性与稳定性。GBGA组合系统的GDOP值远小于单系统的PDOP值,取决于可见卫星数的增加,使得卫星的空间几何构型得到了增强。

3) GPS/BDS/GALILEO组合定位在卫星截止高度角增加的时候,定位优势较为明显,定位精度和稳定性都优于单系统。其中,当截止高度角在15°、20°时,GBGA的定位精度比单GPS系统的定位稍差,但在截止高度角达到30°、40°时,由于GPS可见卫星数的减少,GPS系统的历元可用度分别为92%、48%,此时GBGA组合系统在X、Y、Z方向的定位结果都较单系统平稳,定位精度优于单系统。

[1] 杨元喜.北斗卫星导航系统的发展、贡献与挑战[J].测绘学报,2010,39(1):1-5.

[2] 李博,徐爱功,祝会忠,等.不同截止高度角BDS/GPS伪距单点定位性能分析[J].测绘科学,2016,41(12):32-38.

[3] 罗小敏,蔡昌盛.GPS/GALILEO组合单点定位精度分析[J].大地测量与地球动力学,2013,33(3):137-140.

[4] 魏二虎,刘学习,刘经南.北斗+GPS组合单点定位精度评价与分析[J].测绘通报,2017(5):1-5.

[5] 李林红,何绣凤,张化凝.COMPASS伪距单点定位精度分析[J].大地测量与地球动力学,2013,33(2):58-62.

[6] 邹波,李小莉,陶庭叶.GPS/BDS组合系统伪距单点定位模型精度分析[J].测绘科学,2014,39(10):30-32+59.

[7] 袁宏超,秘金钟,高猛,等.双导航定位系统伪距单点定位方法与精度分析[J].导航定位学报,2014,2(3):38-43.

[8] 任晓东,张柯柯,李星星,等.BeiDou、Galileo、GLONASS、GPS多系统融合精度单点[J].测绘学报,2015,44(12):1307-1313.

[9] 安向东.GPS与北斗伪距单点定位性能对比分析[J].全球定位系统,2014,38(3):8-14.

[10] 严超,余学祥,徐炜,等.GPS/BDS/GLONASS组合伪距单点定位性能测试与分析[J].全球定位系统,2017,42(2):25-31.