液压缸活塞微织构化表面动压润滑性能理论研究
张 颖,余 广,曾良才,毛 阳,湛从昌,卢 艳
(武汉科技大学机械自动化学院,湖北 武汉,430081)
液压缸活塞微织构化表面动压润滑性能理论研究
张 颖,余 广,曾良才,毛 阳,湛从昌,卢 艳
(武汉科技大学机械自动化学院,湖北 武汉,430081)
为研究液压缸活塞微织构化表面的动压润滑性能,在液压缸活塞表面加工开口形状为圆形、椭圆形、正方形、正六边形的微织构,利用雷诺方程对活塞表面与液压缸缸筒内圆之间的流场进行数学建模,并采用MATLAB软件进行仿真计算,研究微织构开口形状、活塞运动速度及微织构深径比对活塞表面动压润滑性能的影响。结果表明,在活塞表面加工4种不同开口形状的微织构均可改善活塞表面的动压润滑性能,其中椭圆形微织构的改善效果略差;随着活塞运动速度的提高,不同形貌微织构表面的摩擦因数均增大,活塞表面动压润滑性能变差;圆形微织构的深径比为0.009时,活塞表面的动压润滑性能较佳。
液压缸;活塞;微织构;表面织构;润滑性能;动压润滑
采用激光工艺在试样表面上加工出具有一定形状、深度和面积率的微织构,能使其减摩抗磨性能显著提高,进而大大减少机械的热损失,延长机械的寿命[1-3]。为此,表面微织构的应用已成为国内外研究者关注的热点。目前关于微织构在径向轴承[4-5]、发动机气缸内表面[6]、刀具表面[7]和合金表面电化学腐蚀[8]等方面的应用研究均有所突破。文献[9]中将微织构应用于伺服液压缸活塞表面,有效减少了其与缸筒内圆表面间的摩擦,但该研究只针对微条纹形貌,而未对其他形貌微织构进行讨论。为此,本文以液压缸缸筒与活塞之间的间隙流场为研究对象,在活塞表面构造不同形状的微织构,运用经典Reynolds方程进行数学建模,用MATLAB软件进行仿真计算,主要研究不同形貌参数的微织构分布在活塞表面时的油膜压力分布,以及在不同微观形貌、活塞运动速度、微织构深径比下活塞表面的动压润滑性能,以期获得润滑性能最佳时活塞表面的微织构形貌及其几何参数。
1 模型的建立
1.1 几何模型
以伺服液压缸为研究对象,在活塞表面加工微织构,微织构在活塞表面呈规则均匀分布。以圆形微织构为例,织构的分布图如图1所示。

图1 活塞表面微织构几何模型
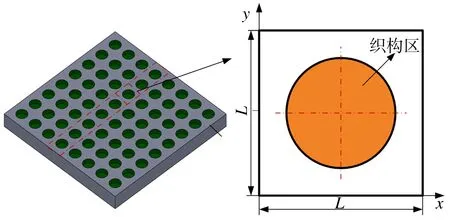
图2 微织构控制单元几何模型
由于间隙油膜厚度和微织构的径向尺寸相对于活塞尺寸较小,因此可以忽略油膜曲率半径的影响,将活塞表面展开成平面[10],选取单个微织构控制单元进行研究,其几何模型如图2所示。沿x、y方向上,控制单元的边长为L,微织构的开口面积为A,则微织构的面积率Sp可表示为
Sp=A/L2
(1)
本文研究4种不同形貌的微织构,其开口形状分别为圆形、椭圆形、正方形和正六边形,具体参数如表1所示。
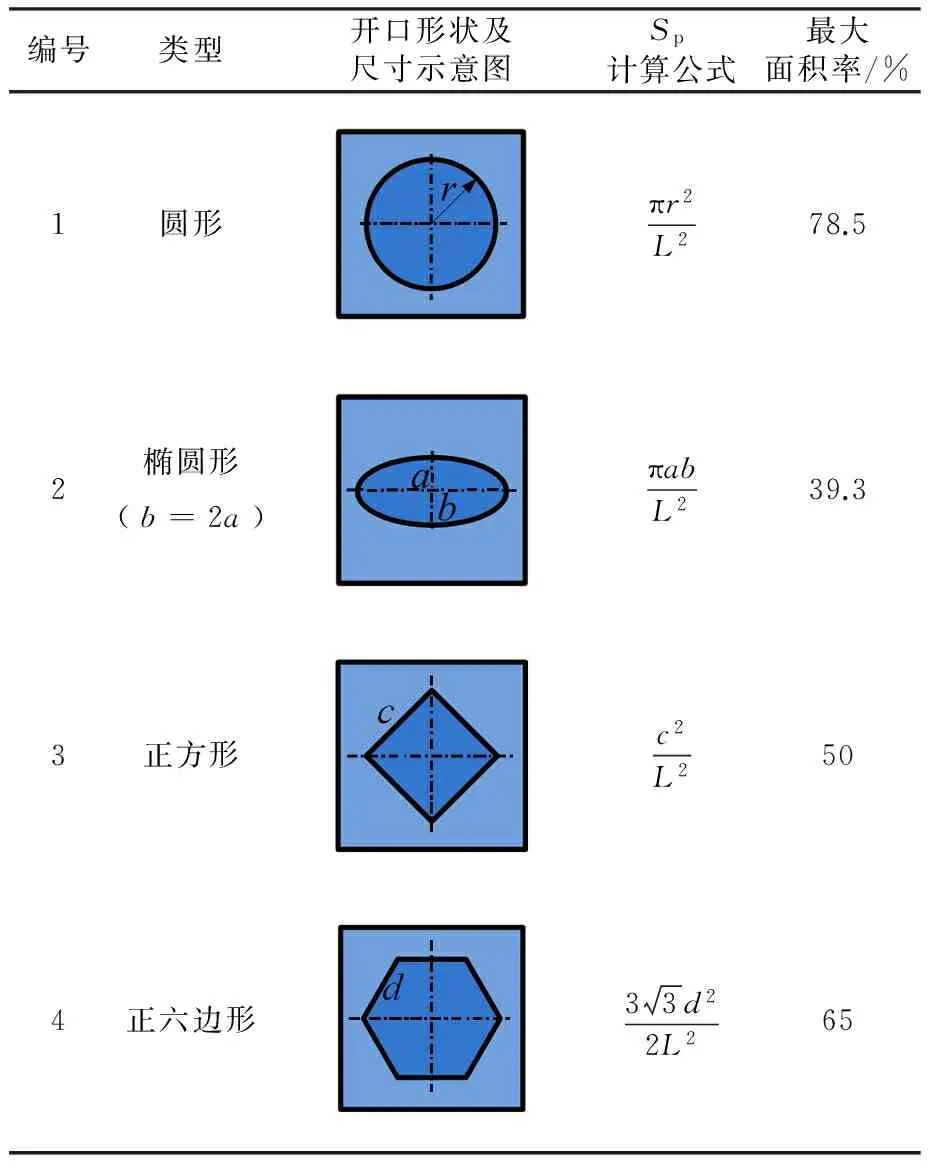
表1 不同形貌微织构控制单元的参数
1.2 膜厚方程
活塞表面单个微织构控制单元的流场截面模型如图3所示,其中U为活塞往复运动速度,h0为最小油膜间隙厚度,hg为微织构开口深度,则微织构流场的实际油膜厚度方程为
(2)
式中:Ω表示凹坑区域。
定义微织构的开口深度hg与最小油膜厚度h0的比值为膜厚比λ,即λ=hg/h0。

图3 单个微织构流场截面模型
目前研究者在探讨织构参数对摩擦因数的影响时,不再单独研究织构直径和织构深度对摩擦因数的影响,而是引入了深径比的概念。深径比一定时,织构直径(或深度)越大,其对应的最优织构深度(或最优织构直径)也越大[11]。
圆形微织构的半径r可表示为
(3)
则其深径比为k=hg/r。
1.3 控制方程
在建立液压缸缸筒-活塞润滑理论控制模型时作如下假设:①液压油在缸筒与活塞表面间无滑动,即贴于活塞表面的油液速度与活塞运动速度相同;②沿油膜厚度方向上不考虑压力变化;③与间隙油膜厚度相比,活塞表面的曲率半径很大,因此忽略油膜曲率的影响;④液压油为牛顿流体;⑤沿间隙油膜厚度方向液压油黏度值不变;⑥不考虑油温变化;⑦缸套与活塞完全同心。
基于以上假设,针对不同开口形状的微织构,采用经典雷诺方程作为其基本控制方程[12]:
(4)
式中:ρ为液压油密度;p为油膜压力;η为液压油的动力黏度。
对上述方程中的各参数进行无量纲化处理,令:
其中:X、Y为无量纲坐标;H为无量纲油膜厚度;P为无量纲油膜压力;η0为液压油动力黏度的初始值。
则式(4)可化简为:
(5)
其中:
(6)
1.4 边界条件
由于微织构间隙流场具有收敛-发散的润滑间隙,根据其几何结构和供油情况确定间隙油膜入口和出口边界。本文采用雷诺空化边界条件[15],其无量纲形式如下:
P(X=0,Y)=P(X=1,Y)=1
(7)
(8)
P(X,Y=0)=P(X,Y=1)
(9)
1.5 摩擦因数的求解
由雷诺方程求得微织构表面压力分布后,在整个控制单元范围内,将无量纲油膜压力积分,可求得润滑油膜的无量纲承载量,即
(10)
考虑活塞表面只受油膜压力作用,润滑油膜作用在固体表面的摩擦力FH可以由与表面接触的流体层中的剪应力沿整个控制单元范围内积分求得,即
(11)
将摩擦力除以油膜承载力,即可得到活塞表面的摩擦因数μ为
(12)
1.6 迭代求解
对方程(5)采用有限差分法进行差分处理,得到离散方程,再用超松弛迭代法对离散后的方程进行迭代求解,得出微织构表面油膜压力分布。超松弛迭代方程如下:
Pn+1=Pn+ω(Pn+1-Pn)
(13)
式中:n为迭代次数;ω为超松弛迭代因子,一般取0.95~1。
设上述方程的迭代收敛因子为ε,则收敛条件为
(14)
最后采用辛普森公式[16]对式(10)、式(11)进行积分求解,再通过式(12)运算得出微织构表面的摩擦因数。
2 动压润滑性能分析
利用MATLAB软件对单个微织构控制单元活塞表面与液压缸缸筒内圆之间的流场进行仿真,得到油膜厚度及油膜压力分布,从而求得活塞表面的摩擦因数。
2.1 不同形貌微织构活塞表面的动压润滑性能
面积率Sp=30%、控制单元边长L=1.5 mm、液压油动力黏度η=0.89 Pa·s、表面粗糙度为Ra0.8、活塞运动速度U=0.6 m/s、环境压力p0=101 325 Pa、最小油膜厚度h0=2 μm、微织构深度hg=10 μm时,不同微织构表面的无量纲油膜厚度如图4所示。
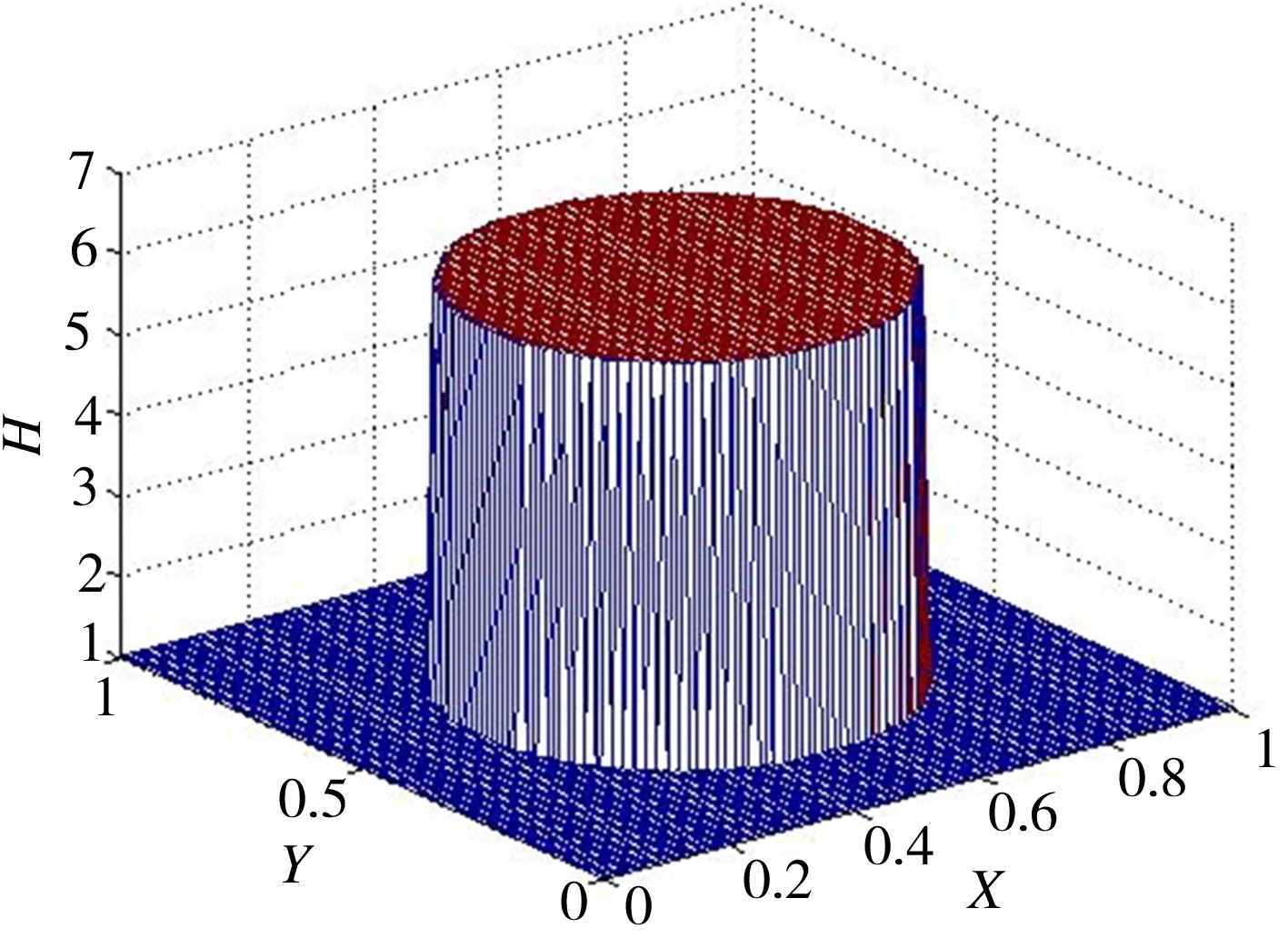
(a)圆形
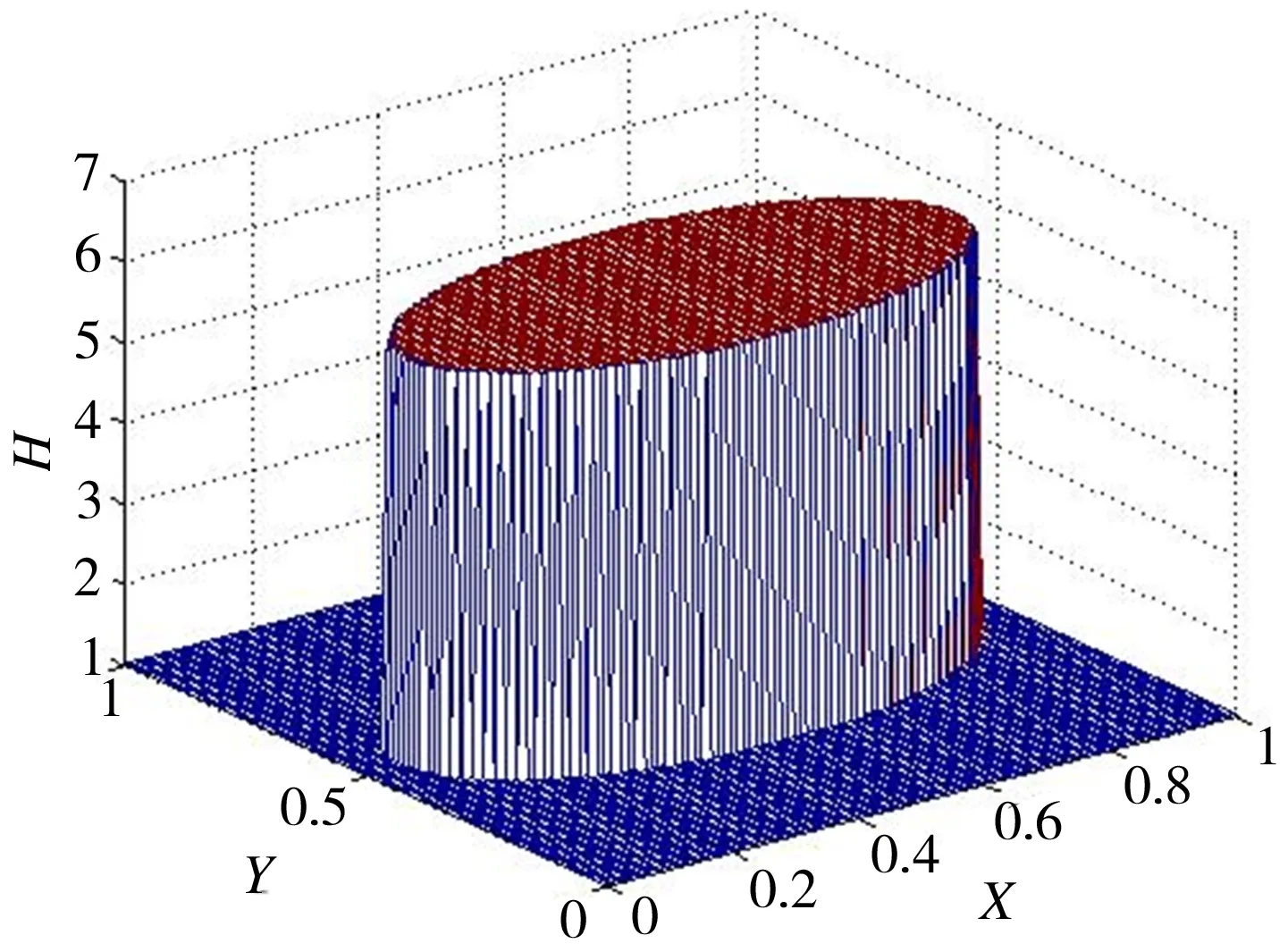
(b) 椭圆形
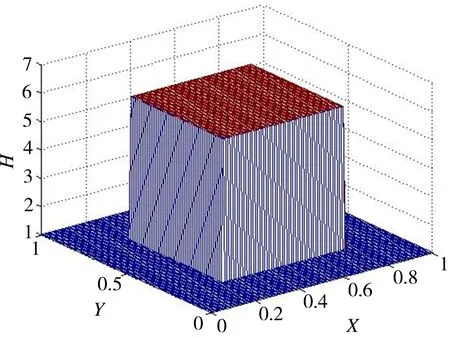
(c) 正方形
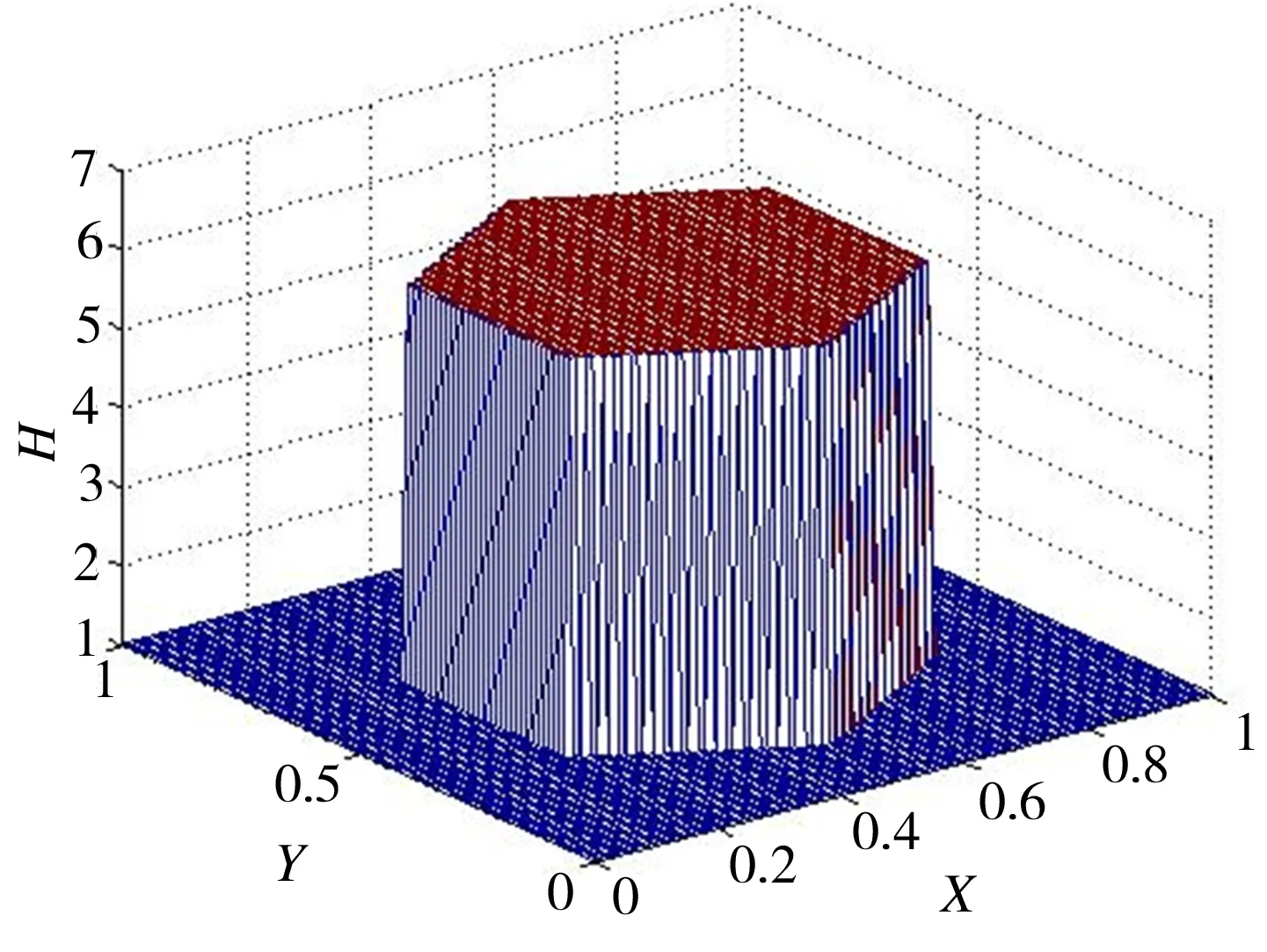
(d) 正六边形
图5所示为不同形貌微织构活塞表面的油膜压力分布。从图5中可以看出,不同形貌的微织构表面均能产生动压,虽然各自压力的分布不同,大小也有所差异,但压力峰值所在的区域大致相同,均位于开口区域的右侧。这是因为微织构在运动过程中,其左侧相当于微轴承的发散楔,压力低于油液的饱和蒸气压,而右侧相当于微轴承的收敛楔,压力在此达到最大。
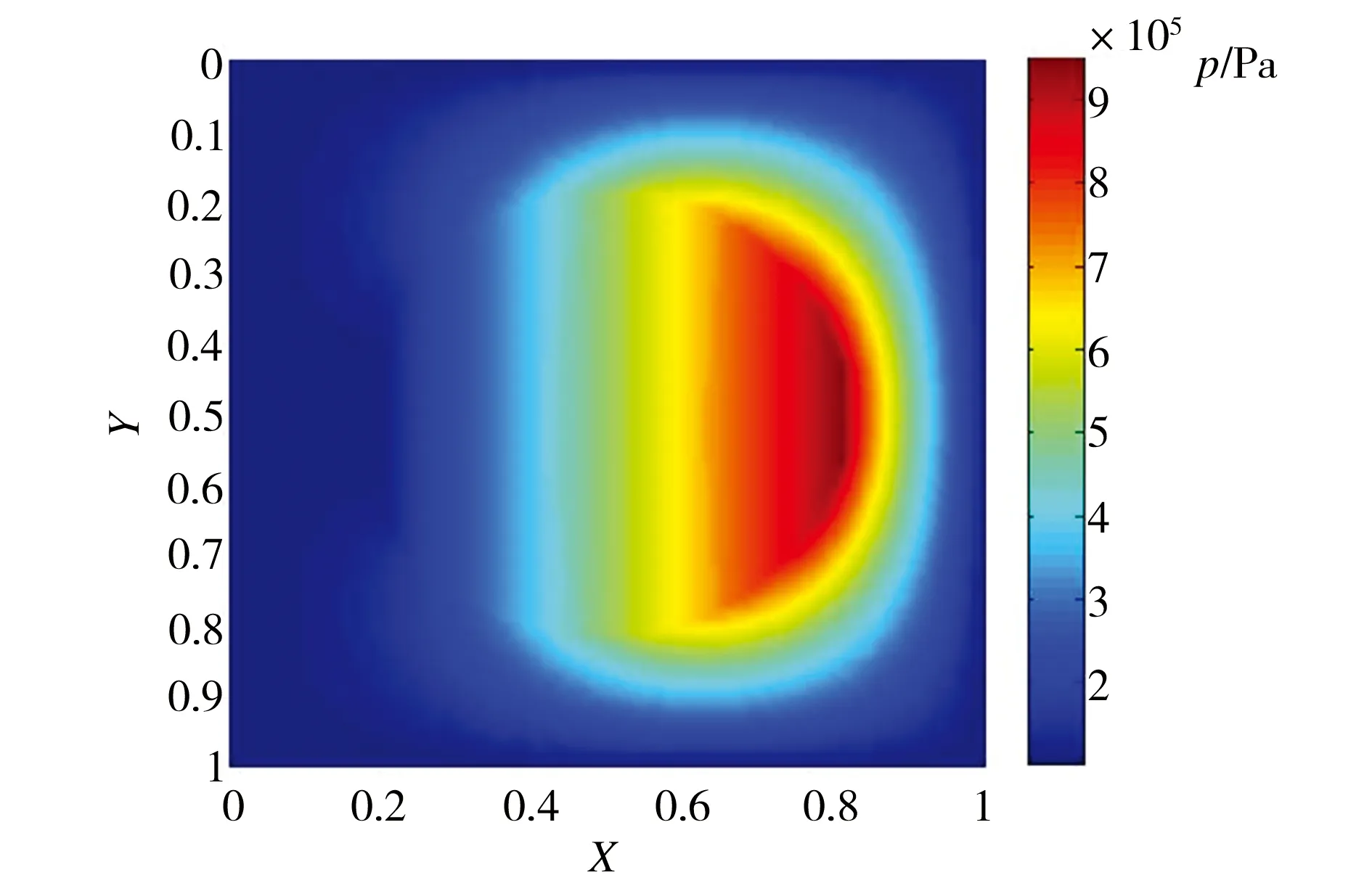
(a)圆形
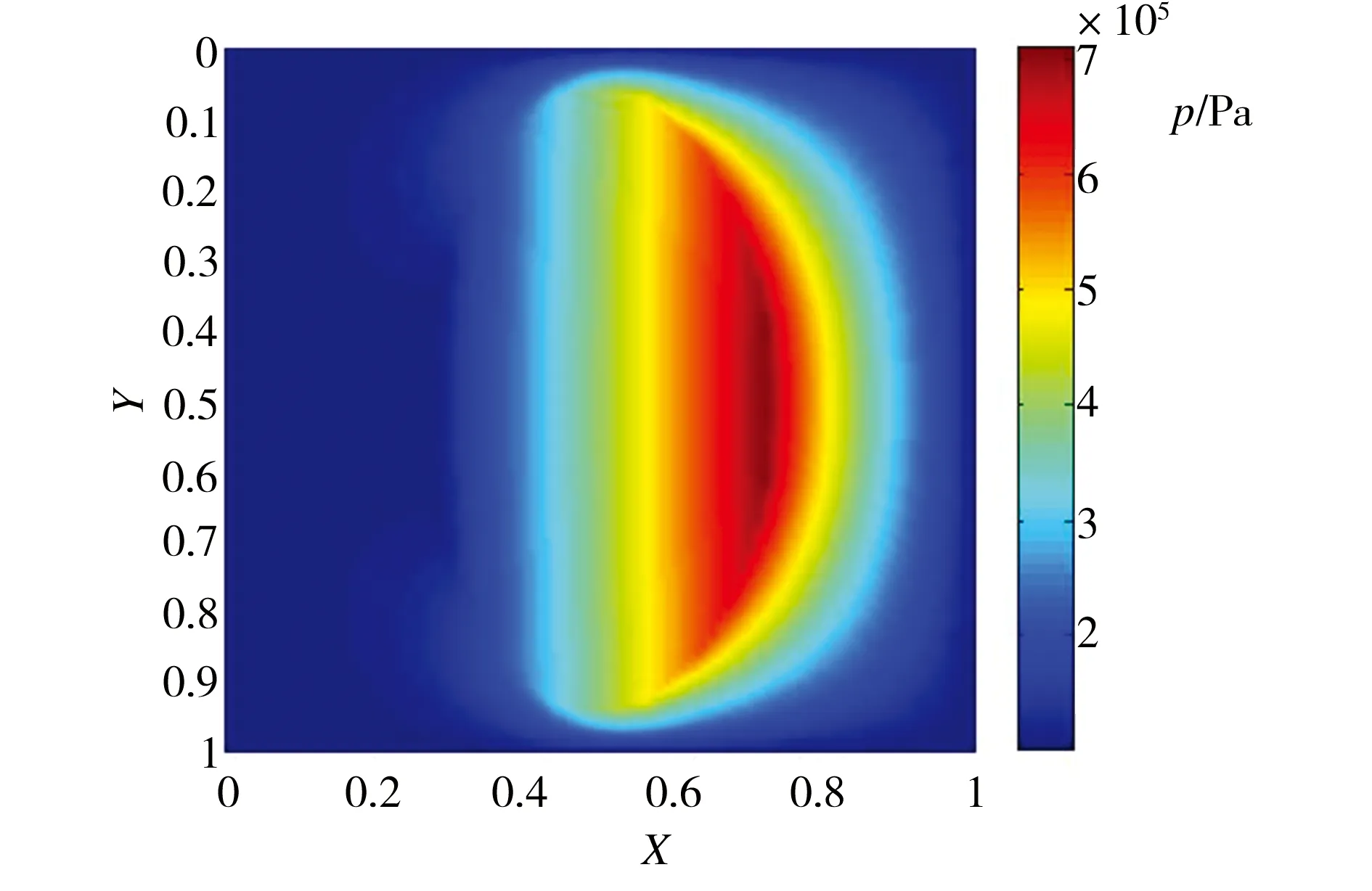
(b) 椭圆形
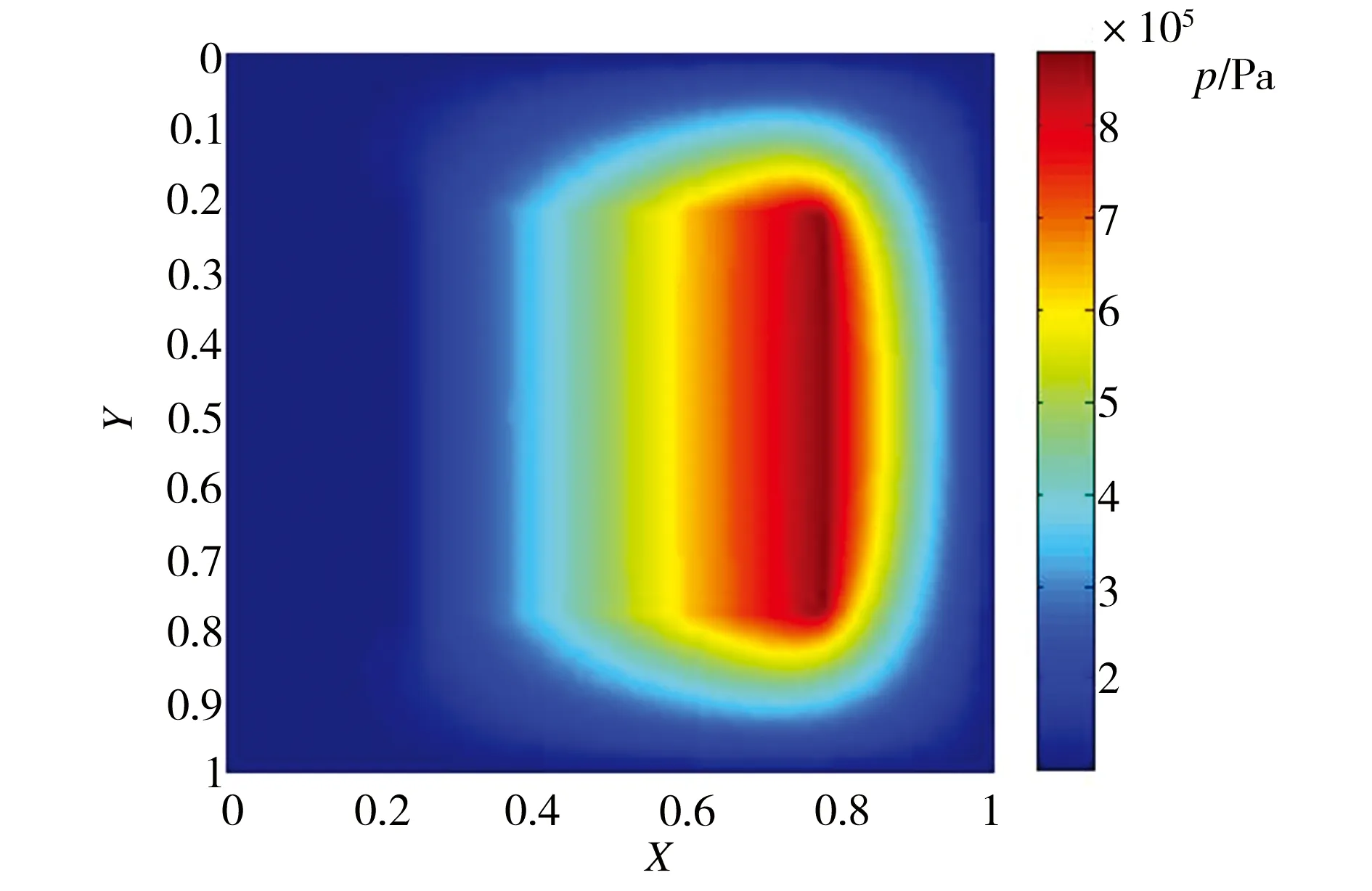
(c) 正方形
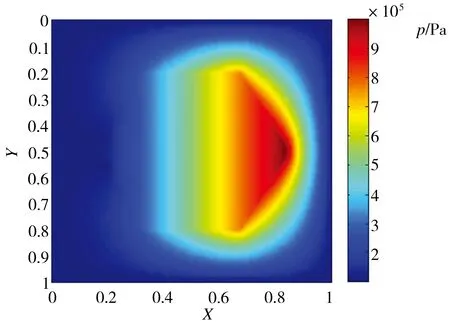
(d) 正六边形
图6所示为无织构表面和面积率均为0.3的4种微织构活塞表面的摩擦因数对比图。从图6可见,无织构表面的摩擦因数最大,加工微织构后表面摩擦因数大幅度降低,相对于无织构表面,有织构的表面摩擦因数减小了41.39%~62.17%;在面积率相同的情况下,4种微织构表面中,开口形状为椭圆的微织构摩擦因数最大,而其他3种微织构摩擦因数相差不大,表明椭圆形微织构对活塞表面润滑性能的改善效果不如其他3种开口形状的微织构。这主要是由于椭圆形微织构沿运动方向的长度大于垂直运动方向的长度,对流体的流动起到了一定的阻碍作用。
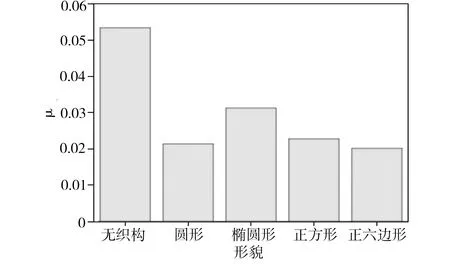
图6 不同形貌活塞表面的摩擦因数
2.2 不同活塞运动速度下微织构活塞表面的动压润滑性能
在面积率Sp=0.3、膜厚比λ=1时,不同活塞速度下微织构活塞表面的摩擦因数如图7所示。从图7中可以看出,随着活塞运动速度的增大,不同微织构表面的摩擦因数均增大,表明不同形貌微织构表面的动压润滑性能均随活塞运动速度的提高而下降。
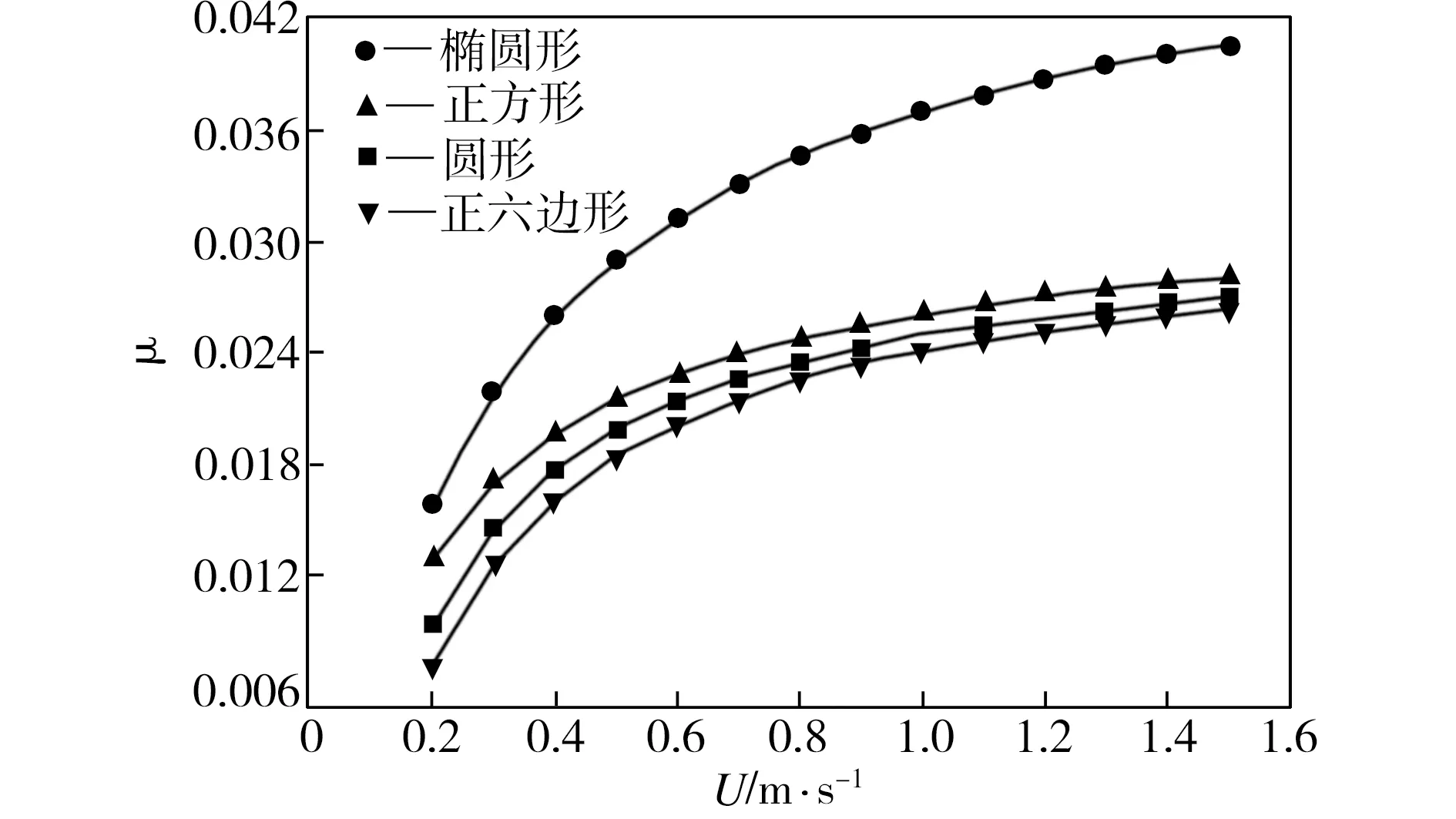
图7 活塞运动速度对微织构表面摩擦因数的影响
2.3 不同深径比下微织构活塞表面的动压润滑性能
开口形状为圆形、膜厚比λ=1、开口深度hg=10 μm时,微织构活塞表面的摩擦因数随面积率的变化情况如图8所示。从图8中可以看出,不同活塞运动速度下微织构表面的摩擦因数μ随着面积率Sp的增大均呈先减小后增大的变化趋势,即存在一个最优的面积率使得微织构表面的摩擦因数最小,动压润滑性能最好,由图8可知,最优面积率Sp=0.3~0.5。
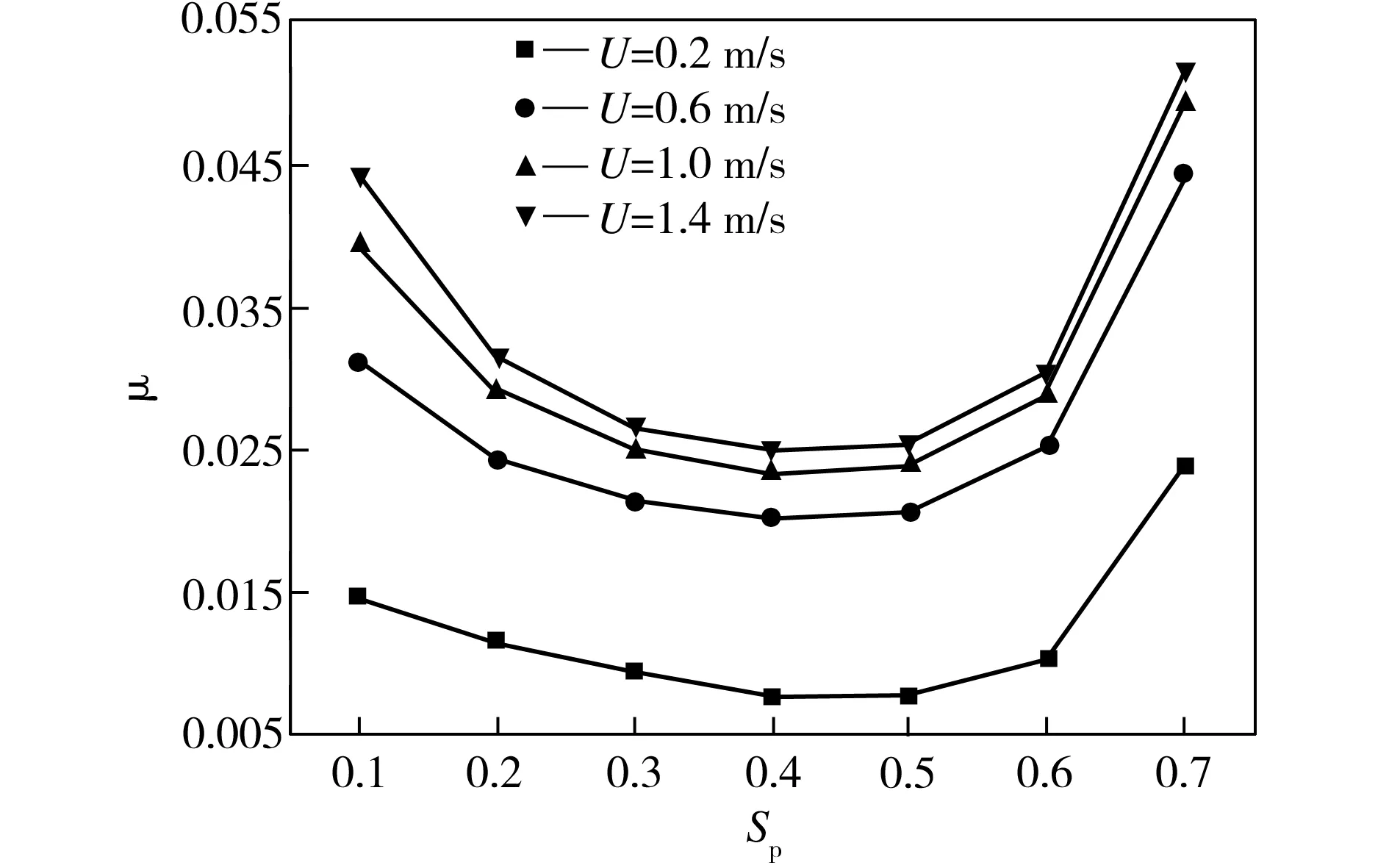
图8 面积率对微织构表面摩擦因数的影响
再将面积率转化为深径比进行深入分析。开口形状为圆形、膜厚比λ=1、面积率在0.3~0.5之间时,不同活塞运动速度下深径比对微织构活塞表面摩擦因数的影响如图9所示。由图9中可见,摩擦因数μ随着深径比的增大呈先减小后增大的变化趋势,表明存在一个最优深径比,使摩擦因数最小,动压润滑性能最好,从图9中可以看出,最优深径比为k=0.009。
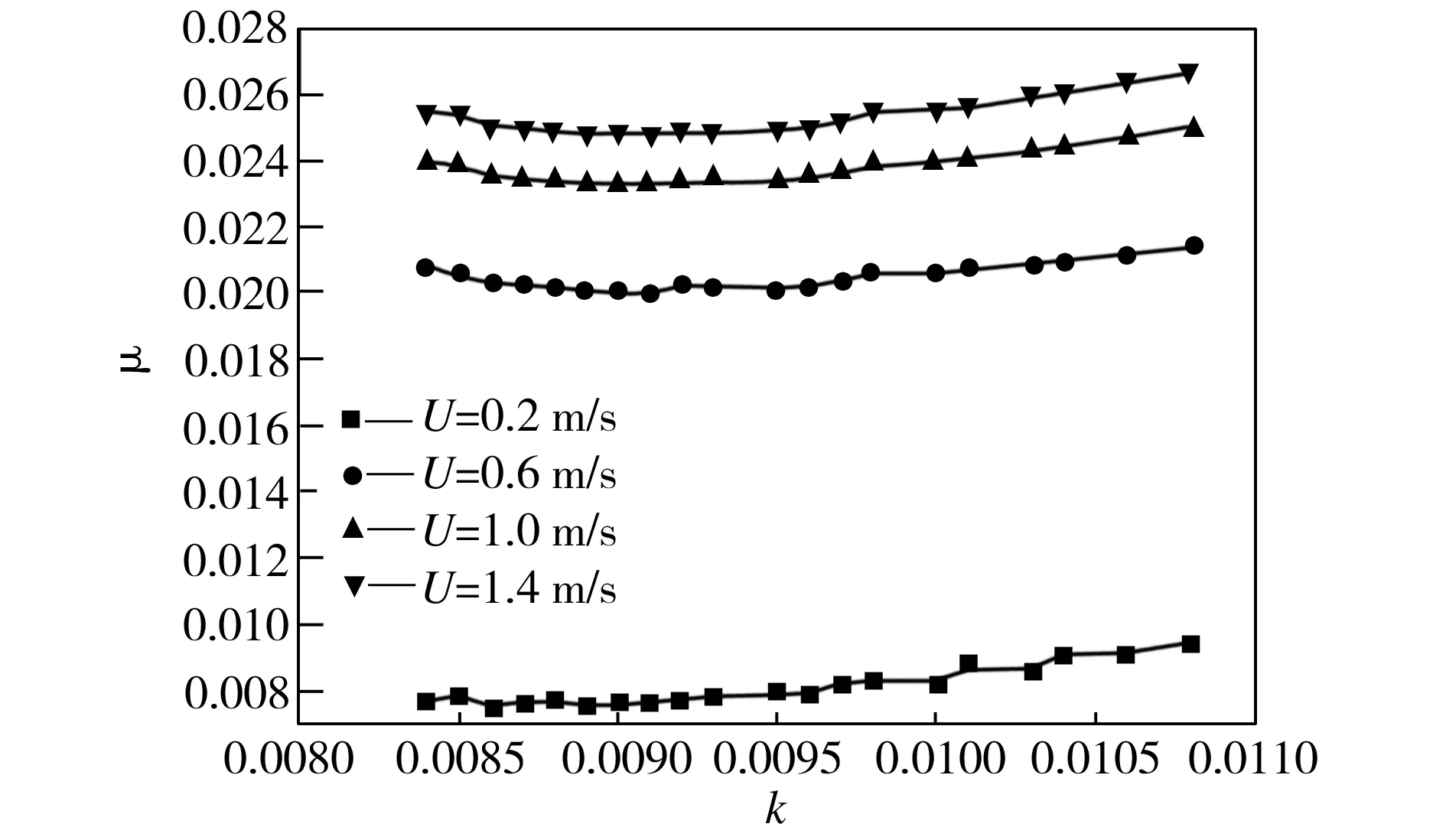
图9 深径比对微织构表面摩擦因数的影响
3 结论
(1)在液压缸活塞表面加工开口形状为圆形、椭圆形、正方形、正六边形的微织构均能降低其摩擦因数,提高其动压润滑性能,而且面积率一定时,微织构形貌的不同对表面摩擦因数的影响不大,只有椭圆微织构活塞表面的动压润滑性能略差。
(2)随着活塞运动速度的提高,不同形貌微织构表面的摩擦因数均增大,其中开口形状为椭圆的微织构表面动压润滑性能所受影响最大。
(3)圆形微织构表面动压润滑效果最佳时,微织构的深径比为0.009。
[1] 刘强,林乃明,邹娇娟,等. 改善钢铁材料摩擦学行为的表面织构研究现状[J]. 表面技术,2016,45(5):41-50.
[2] 郑锦华, 吴双, 魏新煦,等.研磨抛光表面微孔织构的形成 [J].光学精密工程, 2016,24(4):788-795.
[3] 纪敬虎,符永宏,王祖权,等. 激光表面跨尺度织构化机械密封摩擦性能[J].排灌机械工程学报,2012,30(4):452-456.
[4] 张金煜,孟永钢. 推力滑动轴承表面织构的优化设计[J]. 机械工程学报,2012,48(17):91-99.
[5] 尹明虎,陈国定,高当成,等. 3种微织构对径向滑动轴承性能的影响[J].哈尔滨工业大学学报,2016,48(1):159-164.
[6] 陈世平,刘艳中,杜江,等. 发动机气缸内表面激光微织构工艺试验研究[J]. 现代制造工程,2015(11):99-105.
[7] 吴泽,邓建新,亓婷,等. 微织构自润滑刀具的切削性能研究[J]. 工具技术,2011,45(7):18-21.
[8] 周建忠,梅於芬,盛杰,等.激光喷丸诱导镁合金表面微织构的电化学腐蚀性能[J].机械工程学报,2015,51(16):120-126.
[9] 余广, 曾良才, 毛阳,等. 液压缸活塞表面微条纹织构摩擦性能数值分析[J].武汉科技大学学报, 2015,38(6):436-439.
[10]符永宏,张华伟,纪敬虎,等. 微造型活塞环表面的润滑性能数值分析[J].内燃机学报, 2009, 27(2): 180-185.
[11]马晨波,朱华,孙见君. 椭圆形截面织构的最优参数设计模型[J].中南大学学报:自然科学版,2012,43(3):953-959.
[12]刘素梅,刘惠梅. 一种简化雷诺方程的数值求解方法[J]. 中北大学学报:自然科学版,2006,27(2):165-167.
[13]Patir N,Cheng H S. An average flow model for determining effects of three-dimensional roughness on partial hydrodynamic lubrication[J].Journal of Lubrication Technology,1978,100:12-17 .
[14]Patir N,Cheng H S.Application of average flowmodel to lubrication between rough sliding surfaces[J].Journal of Lubrication Technology,1979,101:220-229.
[15]于海武,王晓雷,孙造,等. 圆柱形微凹坑表面织构对流体动压润滑性能的影响[J].南京航空航天大学学报,2010,42(2):209-213.
[16]刘智颖,王向公,任威龙,等. 辛普森公式的推广形式及应用[J].山东理工大学学报:自然科学版,2014,28(1):29-31.
[责任编辑 郑淑芳]
Theoretical stydy on hydrodynamic lubrication performance of micro-texture on the hydraulic cylinder piston surface
ZhangYing,YuGuang,ZengLiangcai,MaoYang,ZhanCongchang,LuYan
(College of Machinery and Automation, Wuhan University of Science and Technology, Wuhan 430081, China)
In order to study the hydrodynamic lubrication performance of the hydraulic cylinder piston textured surface, this paper, considers four micro-texture opening shapes (circle, ellipse, diamond, and hexagon) on the hydraulic piston surface and using Reynolds equation, establishes the mathematical model of the flow field of a single micro-texture control unit between the piston surface and the inner circle of the cylinder. MATLAB is used for numerical calculations, and the influence of micro-texture opening shape, velocity of piston, and micro-texture depth-to-diameter ratio on the hydrodynamic lubrication performance of the piston surface is studied. The results show that, all the four opening shapes of micro-texture on the piston surface can improve the hydrodynamic lubrication performance of the piston surface, and among the four opening shapes, elliptical micro-texturing has the poorest effect. With the increase in velocity of piston movement, the friction coefficient of micro-texture surfaces increases, and the hydrodynamic lubrication effect becomes worse. The optimal depth-to-diameter ratio of circular micro-texture is 0.009, in which the hydrodynamic lubrication effect is the best.
hydraulic cylinder; piston; micro-texture;surface texture; lubrication performance; hydrodynamic lubrication
2016-11-04
国家自然科学基金青年科学基金资助项目(51405350).
张 颖(1994-),女,武汉科技大学硕士生.E-mail:15927438288@139.com
曾良才(1964-),男,武汉科技大学教授,博士生导师.E-mail:zengliangcai@wust.edu.cn
10.3969/j.issn.1674-3644.2017.01.011
TH117
A
1674-3644(2017)01-0055-06

