压缩式封隔器胶筒接触力学行为有限元分析
王云学,许仁波,孟奇龙,江 能
(1.武汉科技大学机械自动化学院,湖北 武汉,430081;2. 中国石油化工股份有限公司江汉油田分公司技术监督中心,湖北 潜江,433100)
压缩式封隔器胶筒接触力学行为有限元分析
王云学1,许仁波1,孟奇龙1,江 能2
(1.武汉科技大学机械自动化学院,湖北 武汉,430081;2. 中国石油化工股份有限公司江汉油田分公司技术监督中心,湖北 潜江,433100)
以Y341-114型压缩式封隔器为研究对象,基于Mooney-Rivlin橡胶本构模型,对封隔器胶筒的非线性接触力学行为进行有限元模拟,分析了胶筒轴向压缩距及胶筒与套管壁间接触应力分布与坐封载荷之间的关系。仿真结果表明,封隔器胶筒与套管壁间的接触应力和胶筒轴向压缩距均随坐封载荷的增大而增大;坐封载荷较高时,上胶筒与套管之间的接触应力最大,起主要密封作用的是上胶筒;坐封载荷较低时,中胶筒与套管之间的接触应力最大,起主要密封作用的是中胶筒。
封隔器;胶筒;接触应力;压缩距;坐封;有限元分析
封隔器是油田注水、堵水、试油、压裂以及完井等工艺流程中分隔油层的重要井下工具,其核心部件是胶筒密封元件,胶筒密封效果的好坏将直接影响封隔器井下工作的可靠性[1-3]。封隔器坐封过程中,压缩式胶筒在坐封载荷作用下,产生轴向压缩变形以及径向膨胀变形,使得胶筒与套管壁相互接触产生接触应力,达到密封环分隔油层的目的。胶筒与套管壁间接触应力的大小及其分布情况显然是影响封隔器密封性能的关键因素。因此,胶筒与套管间接触行为的力学分析对明确胶筒密封机理、优化压缩式胶筒设计以及封隔器现场坐封施工具有重要意义。
封隔器胶筒密封元件常用材料为橡胶,具有典型的几何、材料以及边界条件三重非线性,使得对胶筒与套管间接触行为的分析计算存在较大难度[4-5]。目前,国内外主要采用理论分析、室内试验以及数值模拟等方法对胶筒与套管间的接触行为进行研究[6-10]。本文拟以现场使用的Y341-114型液压坐封压缩式封隔器为研究对象,利用SolidWorks软件对其进行实体建模,并基于Mooney-Rivlin橡胶本构模型,对胶筒与套管间接触力学行为进行ANSYS有限元模拟,研究不同坐封载荷下胶筒与套管壁间接触应力的分布及胶筒轴向压缩距的变化规律。
1 胶筒本构模型及参数确定
1.1 胶筒本构模型
目前,国内外学者大多采用唯象理论来描述橡胶材料的本构关系。唯象理论假设橡胶材料具有各向同性和不可压缩性,并采用应变能密度函数W来描述其本构关系:
W=W(I1,I2,I3)
(1)
式中:I1、I2、I3为变形张量不变量。
根据应变能密度函数的不同,橡胶材料的唯象模型包括:Mooney-Rivlin模型、Yeoh模型、Valanis-Landel模型和Ogden模型。Mooney-Rivlin模型是一种比较常用的橡胶本构模型,其结构形式简单,参数易于确定,几乎适用于橡胶材料的所有力学行为模拟[5]。黄建龙等[11]采用此模型模拟了超弹性橡胶材料的接触力学行为,并得到较为理想的结果。为此,本文接触行为有限元分析中采用二参数的Mooney-Rivlin模型,具体形式如下[5]:
W=C1(I1-3)+C2(I2-3)
(2)
式中:C1和C2为Rivlin系数。
1.2 胶筒模型参数的确定
利用二参数Mooney-Rivlin模型,对胶筒与套管间接触行为进行有限元模拟分析,首先应确定橡胶材料性能参数以及Mooney-Rivlin模型的相关参数。Y341-114型封隔器胶筒橡胶材料为氢化丁腈,工作温度120 ~150 ℃,最大工作压差35 MPa。根据现场参数,可确定氢化丁腈橡胶的力学性能参数。确定Mooney-Rivlin模型参数的方法主要有两种:一是通过实验,即单轴拉伸、压缩实验和剪切实验确定;二是利用经验公式确定[12]。本文利用经验公式得到Mooney-Rivlin模型中常数C1、C2分别为2.3255和1.1627。
2 有限元分析
2.1 有限元模型的建立
Y341-114型封隔器密封部件由单向加压的三级胶筒、中心管、隔环、套管、推力座、护腕以及胶筒座等组成,如图1所示。
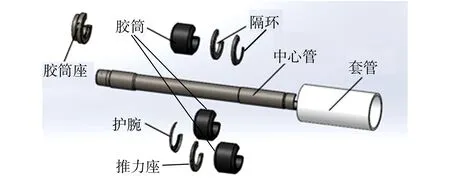
图1 Y341-114封隔器胶筒爆炸图
为建立有限元分析模型,首先以Y341-114型封隔器实际结构及尺寸为依据,借助SolidWorks软件进行实体建模,然后导入ANSYS软件构建有限元分析模型。考虑到封隔器密封部分属于轴对称结构,为减少计算量,简化有限元模型如图2所示。有限元模型中的中心管、隔环、套管、护腕、推力座和胶筒座,在轴向载荷作用下变形很小,与胶筒相比可忽略不计,故将其视为刚性体。在对有限元模型划分网格时,为保证计算精度,对3个胶筒进行网格单元细化(见图2)。
2.2 约束与载荷
结合Y341-114型封隔器的实际工况,对中心管、套管和胶筒座施加Fixed Support约束,即约束X、Y方向的自由度;同时对活塞外侧施加Displacement约束,约束X方向,即推力座只能沿Y轴正方向(向上)运动压缩胶筒。有限元分析过程采用位移加载方式,选取推力座上边线为载荷施加线,约束其X方向自由度,并根据实际工况设定Y方向位移载荷为50 mm。封隔器胶筒接触行为属于大变形问题,在分析中应打开大变形选项。

图2 有限元模型网格图
3 仿真结果分析
3.1 接触应力分析
为明确封隔器坐封过程中胶筒轴向压缩距及胶筒与套管壁间接触应力分布与坐封载荷之间的关系,本文选取加载过程中5个不同的时间点进行详细分析,其中包括胶筒与套管壁开始接触点及加载结束点。根据有限元分析结果,可确定5个时间点所对应的坐封载荷,并可根据压强公式求得对应的坐封压力,具体数值如表1所示。

表1 各时间点对应的坐封载荷和坐封压力
为便于分析讨论坐封载荷与压缩距及接触应力分布之间的关系,应力云图中以坐封载荷值代替时间点进行图形标识,得到不同坐封载荷下的接触应力分布云图如图3所示。从图3中可以看出,高载与低载条件下接触应力的分布情况不同,当坐封载荷较低时(见图3(a)、(b)),封隔器中胶筒与套管接触应力最大,其次是上胶筒,接触应力最小的是下胶筒,3个胶筒的最大接触应力均在中间部分,起主要密封作用的是中胶筒;当坐封载荷逐渐增大到较高值时(见图3(c)~(e)),接触应力最大值开始转移到上胶筒处,上胶筒与套管壁之间接触应力开始迅速增大,中胶筒接触应力较小,下胶筒接触应力最小,起主要密封作用的是上胶筒。由图3还可看出,封隔器整个工作过程中,随着坐封载荷的升高,胶筒与套管接触应力逐渐增大,且上胶筒与套管最大接触应力所在位置慢慢向下端靠近,这主要是由于上胶筒上端的护腕罩住封隔器与套管之间的环形间隙,阻止胶筒从此环隙中突出,而上胶筒被压实后,坐封载荷的增大将迫使胶筒向下端变形,最大接触应力点开始向下端转移。
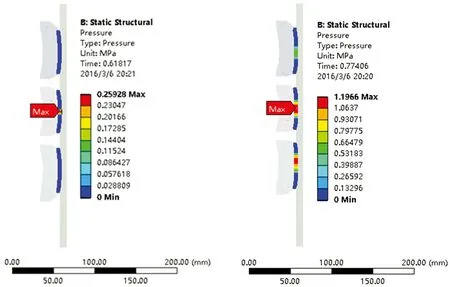
(a)14.4 kN
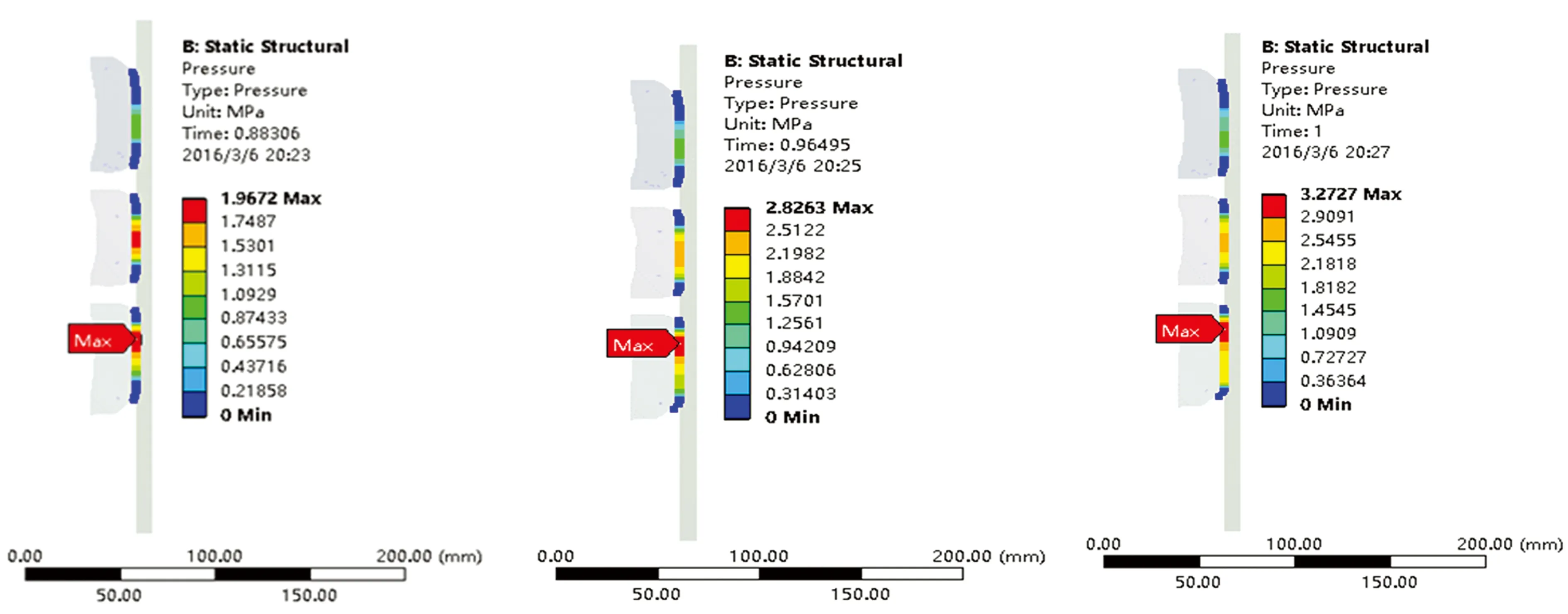
(c)42.6 kN (d)59.4 kN (e)69.7 kN
3.2 轴向压缩距分析
胶筒轴向压缩距与坐封载荷之间的关系如图4所示。从图4中可看出,轴向压缩距随坐封载荷的增大而增大,且开始阶段轴向压缩距增大较明显,这是由于当坐封载荷较小时,胶筒并未与套管壁相接触,处于自由变形阶段,因此轴向压缩距随坐封载荷增加变化趋势明显;当坐封载荷达到15 kN时,轴向压缩距变化趋势开始减缓,结合图3(a)可知,此时封隔器中胶筒开始与套管壁接触产生接触应力,套管对胶筒变形产生径向约束作用,导致轴向压缩距随坐封载荷的增加变化趋势开始变缓;当坐封载荷达到50 kN时,轴向压缩距变化趋势进一步减缓,这可能是因为胶筒接触套管壁后,隔环、套管、护腕分别限制了胶筒的轴向变形与径向变形,其压缩变形趋势减缓。
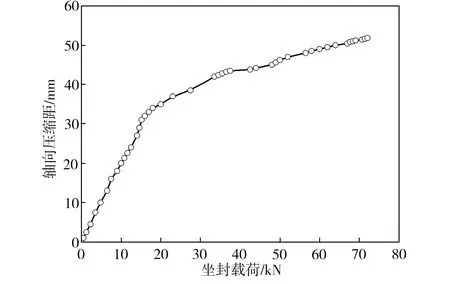
图4 胶筒轴向压缩距和总坐封载荷的关系
4 结论
(1)Y341-114型封隔器胶筒与套管壁间的接触应力和胶筒轴向压缩距均随坐封载荷的增大而增大。
(2)坐封载荷较高时,上胶筒与套管之间的接触应力最大,起主要密封作用的是上胶筒;坐封载荷较低时,中胶筒与套管之间的接触应力最大,起主要密封作用的是中胶筒。
[1] 江汉石油管理局采油工艺研究所. 封隔器理论基础与应用[M]. 北京: 石油工业出版社, 1983.
[2] 王海兰. 井下封隔器工作行为仿真研究[D]. 南充:西南石油大学,2004.
[3] 王祥立. 长胶筒封隔器的研制与应用研究[D]. 北京:中国石油大学(北京),2009.
[4] 李晓芳,杨晓翔,王洪涛. 封隔器胶筒接触应力的有限元分析[J]. 润滑与密封,2005(5): 90-92,125.
[5] 陈家照, 黄闽翔, 王学仁, 等. 几种典型的橡胶材料本构模型及其适用性[J]. 材料导报,2015,29 (S): 118-120,124.
[6] 张劲, 李炜, 张士诚. 封隔器超弹性胶筒力学性能的试验研究[J]. 机械工程学报,2011,47(8): 71-76.
[7] 张晓林, 张棣, 武玉贵, 等. 封隔器胶筒结构优化及优化方法比较[J]. 石油机械,2013,41(6): 101-105.
[8] 王尊策, 管翠翠, 温后珍, 等. Y341-114型注水封隔器胶筒与套管摩擦力试验研究[J]. 石油矿场机械,2012,41(7): 66-69.
[9] 练章华, 乐彬, 宋周成, 等. 封隔器坐封过程有限元模拟分析[J]. 石油机械,2007(9): 19-21.
[10]尹飞, 高宝奎, 金磊. 压缩式封隔器坐封力学有限元分析[J]. 石油机械,2012,40(2): 39-41.
[11]黄建龙, 解广娟, 刘正伟. 基于Mooney-Rivlin和Yeoh模型的超弹性橡胶材料有限元分析[J]. 橡塑技术与装备,2008,34(12): 22-26.
[12]刘萌, 王青春, 王国权. 橡胶Mooney-Rivlin模型中材料常数的确定[J]. 橡胶工业, 2011, 58(4): 241-245.
[责任编辑 郑淑芳]
Mechanical behaviors of contact of compressive packer’s rubber sleeve: a finite element analysis
WangYunxue1,XuRenbo1,MengQilong1,JiangNeng2
(1.College of Machinery and Automation, Wuhan University of Science and Technology, Wuhan 430081, China; 2. Jianghan Oilfield Branch of Sinopec Group, Qianjiang 433124, china)
Based on Mooney-Rivlin constitutive model of rubber, the nonlinear mechanical behaviors of contact between rubber sleeve and casing pipe of Y341-114 compressive packer were simulated by finite element method, and the relationships of axial compressive distance and distribution of contact stress with setting loads were determined. Simulation results show that both the contact stress between rubber sleeve and casing pipe and the axial compressive distance of rubber sleeve increase with the increase of setting loads. Under high setting loads, the maximum contact stress is generated between the upper rubber sleeve and the casing pipe, and the main sealing effect comes from the upper rubber sleeve. However, under low setting loads, sealing is mostly from the middle rubber sleeve.
packer; rubber sleeve; contact stress; compression distance;setting; finite element analysis
2016-07-22
国家自然科学基金资助项目(51175386); 武汉科技大学冶金装备及其控制省部共建教育部重点实验室开放基金项目(2013B04).
王云学(1989-),男,武汉科技大学硕士生.E-mail:599104909@qq.com
许仁波(1977-),男,武汉科技大学副教授,博士.E-mail:xurenbo@wust.edu.cn
10.3969/j.issn.1674-3644.2017.01.012
TE932
A
1674-3644(2017)01-0061-04

