基于属性差异的产品缺陷数据关联规则模糊分类
李 怡,孔建益,王兴东,刘军伟
(武汉科技大学机械自动化学院,湖北 武汉,430081)
基于属性差异的产品缺陷数据关联规则模糊分类
李 怡,孔建益,王兴东,刘军伟
(武汉科技大学机械自动化学院,湖北 武汉,430081)
针对工业生产过程中所产生的产品缺陷数据经过数据挖掘后关联规则存在不能有效组织的问题,提出一种基于项目属性差异的产品缺陷数据关联规则模糊分类方法,在建立模糊分类树的基础上,计算出关联规则间距离,并采用自组织神经网络聚类的方法对挖掘结果进行聚类分析。将该方法应用于冷轧带钢表面缺陷数据挖掘后处理,结果表明,该方法不仅能够得出两种不同属性项目间的关联性,还可以求出缺陷关联规则间的距离,距离越近的关联规则被聚为一类,其相似性越大。
冷轧带钢;产品缺陷;属性;关联规则;模糊分类;距离;聚类分析;可视化
产品表面缺陷数据经过挖掘后,往往会出现大量的关联规则,若直接对这些规则进行数据可视化,所体现出的有效信息会大大减弱,给决策者的判断带来困难,因此,有必要对关联规则的挖掘结果进行再处理。目前关联规则挖掘结果的处理方法主要有聚类法、分组法与剔除法等,其中聚类法是一种通过挖掘数据分布情况来发现数据中隐含模式的一种处理方法,其将大量数据在某种算法下分成多类,使得每一类数据内部存在相似性,而类与类数据之间又存在一定的差异性[1]。关联规则聚类则将挖掘后“亲近”的结果放在一起提供给决策者,便于决策者分析。Toivonen等[2]提出聚类组织关联规则,并根据规则交易数的重合率来得出规则间距离,Strehl等[3]在其基础上作了一些改进,使得距离值控制在区间[0,1]内,但以上方法在计算规则间距离时均须扫描初始数据,不仅耗时,还会形成固定数目的簇而影响对挖掘结果可视化的效果。Chen等[4]提出了模糊分类树的概念,阮备军等[5]在其基础上针对商品分类信息提出一种基于度量关联规则间距离的聚类方法,沈斌等[6]又引入了语义差别,进一步验证了规则聚类的有效性。但是,工业生产中产品缺陷数据与产生缺陷的原因两者不是建立在语义上面的差别,而是属于不同属性类别,因此基于语义差别的聚类方法并不适用。在文献[4]的基础上,刘军伟[7]将两种不同属性项目应用到了模糊分类树中,并且以冷轧带钢表面缺陷为研究对象,挖掘出大量缺陷关联规则,但没有进一步计算关联规则的相似性。基于上述情况,本文提出一种基于属性差异的产品缺陷数据关联规则模糊分类方法,并采用自组织神经网络聚类法(self-organizing map clustering,SOMC)[8]对计算出的缺陷距离矩阵进行总体聚类。
1 关联规则模糊分类方法
1.1 模糊分类树的建立及其属性权值的确定
在模糊分类树中,每个分支可以看作是一类分类树,可以描述为一个有向无环图H=〈I,E,W〉,其中I={i1,…,im}为m个项的集合,E、W分别为有向边和模糊隶属度权值的集合。
图1所示为两种有向无环图,图中项目均属于I集合。若从分类树的结点X到结点Y存在有向边,则称X是Y的祖先,X、Y之间存在祖孙关系,且该关系间具有传递性。连接存在祖孙关系的结点X和结点Y的边序列称为X与Y之间的有向路径,记为l(X,Y)=(e1,e2,…,en) ,其中有向边ei的终点与ei+1的起点一致。
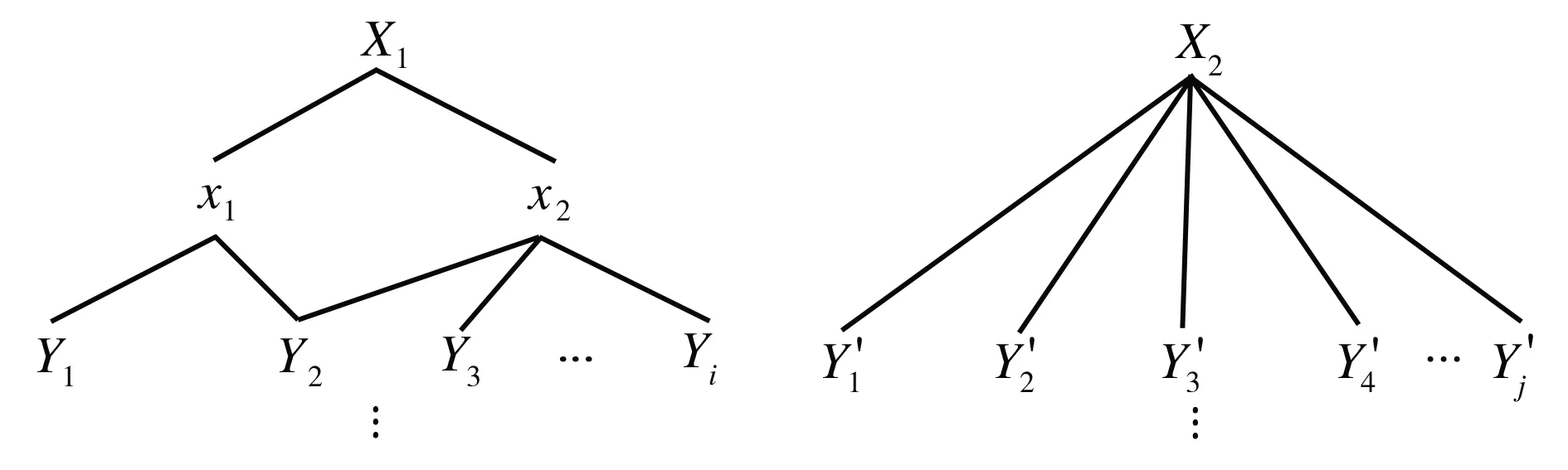
(a)H1
为了便于对分类树中多类属性项目的相似度进行比较,需要将多个有向无环图通过ROOT合并成一个有向无环图。由于项目之间存在一定的属性差异,故需要建立带项目属性差异信息的模糊分类树,具体步骤如下:
第一步,根据项目属性找出分类树中各个项目所在层次。在结构树中,同一层次的项其属性是相同的,因此可根据项目属性找出分类树中各个项目所在的层次,具体过程需遵循以下几点:①合并有向无环图;②根结点ROOT所在层次为1;③有向边起点层次应小于末层次;④不能存在某一层次中不含任何项目的情况;⑤在同一模糊结构树中,处于同一层次的结点项目之间要保证其属性的相似性;⑥模糊结构树中层次间的项目属性级别从大到小依次向下。
将有向无环图H1与H2通过ROOT合并成一个有向无环图,根据以上6项原则得到模糊分类树的结构如图2所示,图中γ为权值。合并后模糊分类树项与项之间有可能存在多个有向边序列,如图2中项目Y2与X1之间就存在两条有向路径:l1={e(X1,x1),e(x1,Y2)},l2={e(X1,x2),e(x2,Y2)}。l1和l2中任意一条有向路径都可以作为具有祖孙关系的X和Y之间的属性相似性通路。

图2 模糊分类树结构
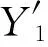
对于同一结构树上两个相邻层次间的项目属性差异,提出如下假设及定义:
假设1设在模糊分类树中,有相邻的两个层次d和d+1(d∈),那么层次d越深,则层次d和d+1之间的项目属性差异就越小。
定义1对于相邻两个层次d和d+1,项目属性差异函数ly(d,d+1)是关于d的函数,即ly(d,d+1)=f(d),并且对于两组相邻层次d1、d1+1和d2、d2+1,当且仅当d1≤d2成立时,ly(d1, d1+1)≥ ly(d2,d2+1)成立。
对于同一结构树上两个不相邻层次间的项目属性差异,有如下假设及定义:
假设2在模糊分类树中,有两组不相邻的层次d、d+n和d′、d′+n′(n、n′、d′∈),若d′≥d,d′+ n′≤ d+n,则ly(d,d+n)≥ly(d′,d′+n′)。
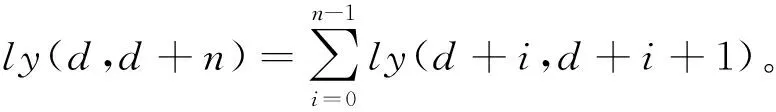
第三步,给模糊结构树中的每个有向边赋予相应的属性差异权值。给出如下定义:
定义3如果给出模糊分类树为H=〈I,E,W〉,则项目属性差异信息的模糊分类树可表示为H=〈I,E,W,W′〉。其中,项目属性权值集合W′是从有向边集合E到正实数集合的映射函数,项目属性差异权值w′(k(x,y))反映了有向边起点项x和终点项y之间的属性差异,它可以由下式得到:
(1)
其中,w(e(x,y))为有向边e的模糊隶属度权值,由W集合给出。一般情况下,有向边的模糊隶属度权值不应取得过小,一般可设置在 [0.5,1]内。
有向边的项目属性差异权值主要由以下两方面的因素决定:其一,ly(d(x),d(y))越大,则有向边的属性差异权值越大,项目属性差异权值w′(k(x,y))也越大;其二,有向边的模糊隶属度权值w(e(x,y))体现了项目属性间相似性度量,即边的模糊隶属度越大,则相似性越高,属性之间差别越小。
设图2所示模糊结构树为4层,如果将相邻的两个不同层次设置为d和d+1,则d的最大取值为3,那么项目属性层次差别函数可以设置为ly(d,d+1)=(3-d+1)/10,该函数的设置是符合定义1的条件的;对于不相邻的两个层次d和d+n,可以将其分解成多个相邻层次,设置项目属性差异函数如定义2中所示。
1.2 基于模糊分类树的距离计算及聚类分析
1.2.1 项间距离
定义4如果x,y∈I,且x与y具有祖孙关系,那么x和y之间的项目属性通路lr(x,y)是x和y之间全部有向路径中所经过边的属性差异权值,即最小的有向路径lmin(x,y),具体可表示为:
(2)
式中:w′(e)为有向边e的两个结点项目之间的属性差异权值。
定义5对于不具备祖孙关系的结点间的属性通路,若项目属性差异信息模糊分类树H=〈I,E,W,W′〉有两条相同起点的有效路径l(x,y)=(e11,e12,…,e1n),l(x,z)=(e21,e22,…,e2m) (x,y,z∈I),那么可以对这两条有向路径进行连接操作,结果记作l(x,y)l(x,z)=(e11,e12,…,e1n, e21,e22,…,e2m)。
定义6对于项目属性差异信息的模糊分类树H=〈I,E,W,W′〉,如果x、y∈I,则项x和y之间的属性通路是边的序列,记为lr(x,y ),可由如下方式得到:
情况1:如果x、y之间存在祖孙关系,设x是y的祖先,那么存在l(x,y),使得lr(x,y)=lmin(x,y)。
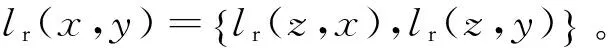
定义7对于模糊分类树H=〈I,E,W,W′〉,若x、y∈I,则项x和y之间的距离定义为
(3)
根据图2中的模糊分类树以及定义5和定义6可得两种情况下项目间的距离值为:
情况1:Ditem(X1,Y2)=lr(X1,Y2)={l1[e(X1,x1);e(x1,Y2)];l2[e(X1,x2);e(x2,Y2)]}min=∑w′(e)。
情况2:Ditem(X1,X2)={lr(ROOT,X1);lr(ROOT,X2)}=w′[e(ROOT,X1)]+w′[e(ROOT,X2)]。
1.2.2 项集间距离
关于项集间距离的定义方法有多种,如最近距离法、最远距离法、平均距离法等,本文采用平均距离法。
定义8存在项集I1={x1,x2,…,xm}和项集I2={y1,y2,…,yn},关于I1和I2之间的项集距离定义为

(4)
如果把项看成网格的结点,项目I的数量看成流量,项目间的差别Ditem的值作为单位费用,那么求项集的最佳匹配实际上是一个最小网络费用流问题,可采用CS2算法进行最小费用流解答[9]。
1.2.3 关联规则间距离
在进行关联规则距离度量的时候,需要考虑结构差别和规则度量差别两个因素,关于其结构距离、度量距离作如下定义:
定义9模糊分类树H=〈I,E,W,W′〉中,如果有关联规则1:X1⟹Y1, 关联规则2: X2⟹Y2, 所有关联规则都为非空子集,且存在非负实数δ1、δ2、δ3,则规则1和2之间的规则结构距离定义如下:
Drule(R1,R2)=δ1Dset(X1∪Y1,X2∪Y2)+
δ2Dset(X1,X2)+δ3Dset(Y1,Y2)
(5)
从定义9中可以看出,关联规则结构差别分为3个部分:前项、后项和并集。其中δ1、δ2、δ3需要根据兴趣爱好进行设定,例如设定δ1=0、δ2=1、δ3=1/3,则表示强调关联规则前项的相似性。从上述公式可以看出,Drule是关于Dset的一个线性组合。
在关联规则距离计算的基础上,采用SOMC法进行可视化分析。
2 实例验证与分析
本文从武汉钢铁(集团)公司二冷轧连退机组钢卷表面质量判定信息数据库中随机抽取15组缺陷数据集合,结合文献[7]数据挖掘结果,采用本文方法对其关联规则进行分类,以验证本文方法的有效性。
2.1 模糊分类树的建立
为方便表述,将不同的钢卷表面缺陷原因及缺陷均用代号表示如下:①缺陷原因:酸洗为S、过酸洗为GS、欠酸洗为QS、乳化液为R;②缺陷:停车斑为TC、锈蚀为XS、氧化皮压入为YH、夹杂为JZ、油斑为YB、黏结为NJ、碳化边为TH、色差为SC、异物压入为YW。以上缺陷主要来自两种不同原因,因此可以建立包含两种有向无环图的模糊分类树,其结构如图3所示。

图3 缺陷及缺陷原因数据模糊分类树
2.2 计算缺陷与缺陷原因属性差异权值
冷轧带钢表面缺陷和缺陷原因各项目之间存在一定的属性差异,故需要建立带属性差异信息的模糊分类树,根据1.1节中描述的步骤建立图4所示带模糊隶属度权值的分类树。

图4 带权值的缺陷及缺陷原因数据模糊分类树
根据1.1节中相关假设及定义,结合文献[7]冷轧带钢表面缺陷相关数据,在此设项目属性差异函数为ly(d,d+1)=(3-d+1)/10,计算可得模糊分类树中有向边的属性差异权值如表1、表2所示。
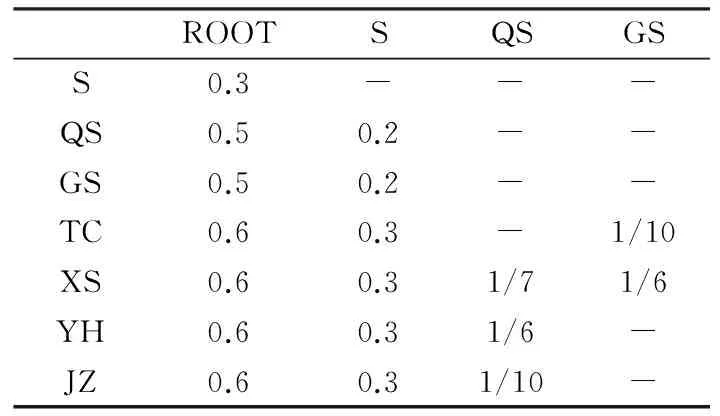
表1 由酸洗产生的缺陷间属性差异权值表

表2 由乳化液产生的缺陷间属性差异权值表
2.3 确定关联规则之间距离
2.3.1 项间距离
根据项间距离中的相关定义,结合表1和表2中的属性差异权值表,分别计算两种情况下的距离值:
情况1:Ditem(S,XS)=lse-r(S,XS)={l1[e(S,GS);e(GS,XS)];l2[e(S,QS);e(QS,XS)]}min=∑w′(e)。
其中,l1[e(S,GS);e(GS,XS)]=0.2+0.17=0.37;l2[e(S,QS);e(QS,XS)=0.2+0.14=0.34;Ditem(S,XS)=0.34。
情况2:Ditem(S,R)={lse-r(ROOT,S);lse-r(ROOT,R)}=w′[e(ROOT,S)]+w′[e(ROOT,R)]=0.3+0.3=0.6。
2.3.2 项集间距离
项集间距离采用CS2算法中计算最小费用流的方法来计算。结合定义8,设有集合I1={TC,XS,YB}和I2={YH,JZ},通过图5所示方法计算可得:Dset(I1,I2)=(0.67+0.6+0.31+0.24+1.47+1.4)/(2×3)=0.782。

图5 最小费用流解答项集间距离求法
用同样的方法计算出多对项集间的距离值如表3所示。由表3可以观察具有祖孙关系的缺陷与不具有祖孙关系的缺陷集合间的距离大小与相似性。
从表3中总体可以看出项集间的距离大小是由两方面决定的,其一,项集间是否具有相同项目;其二,项集间的项目是否属于同一祖先。

表3 多对项集间距离的值
2.3.3 关联规则距离
本文采用文献[7]中的冷轧带钢相关数据进行数据关联规则挖掘,将加权置信度和加权支持度分别设置为0.25和0.0125,采用文献[7]中加权模糊层次关联规则挖掘算法得到关联规则频繁项集有102条,其中缺陷之间二元频繁项集有52条,符合条件的有15条,将得到的关联规则按照产生原因次序排列,根据定义9,将δ1、δ2、δ3分别设置为0、1、1,主要强调前项与后项的作用,最后得到15阶对称矩阵D(15×15)。
为测试本文关联规则距离计算方法的效率,将其与文献[3]、文献[5]和文献[6]中的距离计算方法所需的运行时间进行对比,结果如图6所示。由图6中可见,采用本文方法计算所需的运行时间最短,且随着规则数不断增加,运行时间的变化率呈先慢后快的趋势。
本文方法的优势在于采用文献[7]中加权模糊层次挖掘算法得到缺陷关联规则后,在计算距离时弱化了置信度和支持度之间距离的计算,只强调前项和后项的作用,直接在模糊分类树分层时就赋予各项目的权重值,因此在计算关联规则距离时会比其他方法快一些。
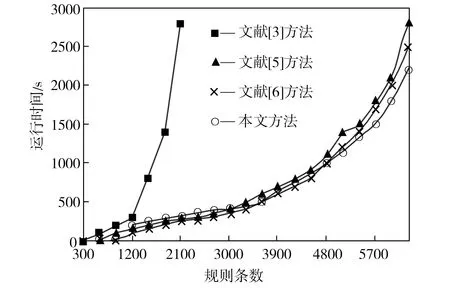
图6 规则距离矩阵计算时间对比
2.4 聚类可视化
在缺陷关联规则距离计算的基础上,采用自组织神经网络聚类法(SOMC)对冷轧带钢缺陷数据挖掘后的关联规则进行聚类分析,整体实施步骤如下:
(1)采用加权模糊层次关联规则挖掘算法对缺陷原因数据进行关联关系数据挖掘,设置好相关参数,剔除原因与原因间的规则以及原因与缺陷间的规则,保留缺陷与缺陷间的规则。
(2)计算关联规则间距离,得到距离矩阵D。
(3)将已经计算好的关联规则距离输入到SOMC工具箱。
(4)分析比较SOMC可视化的结果。实验过程采用SOMC工具箱进行神经网络训练,经过200次Batch算法迭代得到基于关联规则距离的聚类可视化图,如图7所示。图7 (a)中灰色六边形代表神经元(15*15),为距离矩阵训练前状态,图7(b)中红色线连接相邻的神经元(包含有红色线的颜色区域)表示神经元之间的权值距离,即实现这一路径的概率大小,颜色越深代表距离越大,反之则距离越小。图7(b)中以颜色较深处为分界线可将缺陷关联规则距离数据大致划分为8类,表明本文提出的规则聚类方法在组织大量关联规则方面是实用有效的。相比其他的聚类可视化,本文方法更为直观,方便决策者浏览和分析挖掘结果,从而发现其感兴趣的关联规则。
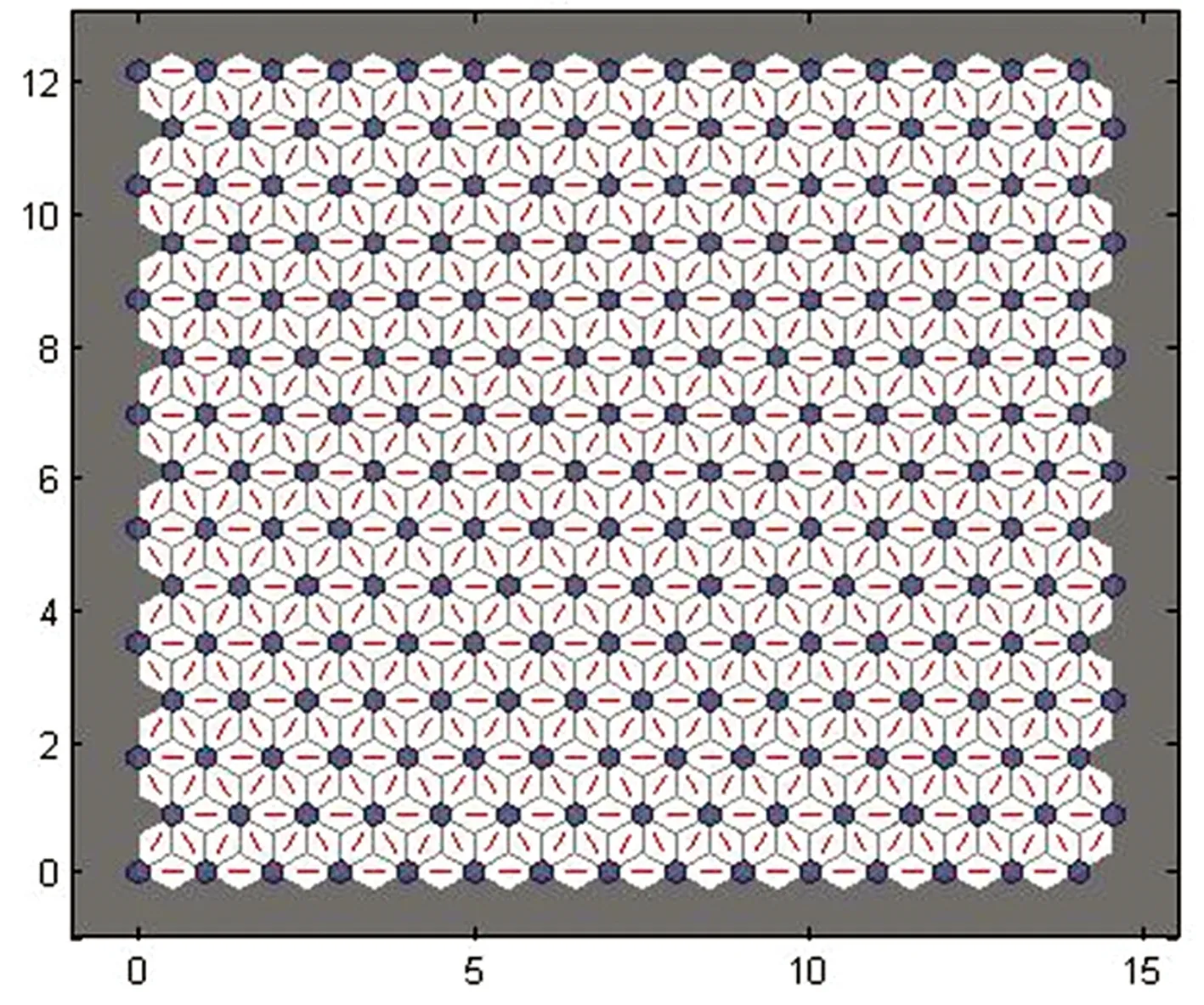
(a)训练前
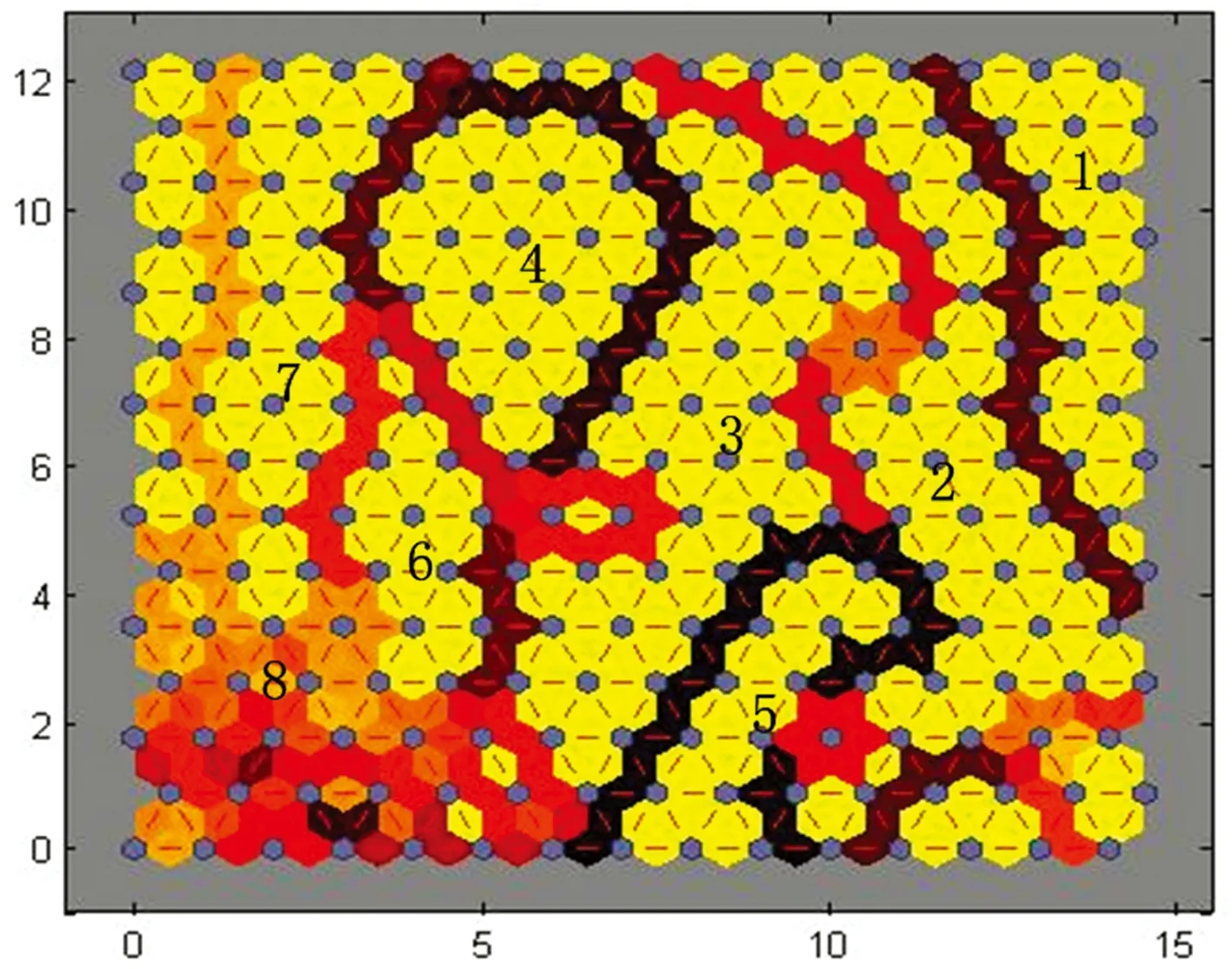
(b)训练后
3 结语
本文提出一种基于属性差异的产品缺陷数据关联规则模糊分类方法,通过缺陷关联规则距离计算和聚类达到关联规则分类的目的。相比以往的研究不同之处在于,该方法通过建立模糊结构分类树提前对关联规则距离进行了求解,进一步缩短了数据扫描的耗时;在进行规则距离计算时,通过给模糊结构分类树层次间添加模糊隶属度,能够更有效建立不同属性项目之间的属性差异;采用SOMC聚类的方法,把高维数据映射到低维输出空间,使得关联规则距离数据更加集中,分类的准确度更高。以冷轧带钢表面缺陷数据为例进行验证,结果表明该方法在处理大量数据关联规则分类问题上是可行的。
[1] Xu R, Wunsch D. Survey of clustering algorithms[J]. IEEE Transaction on Neural Networks, 2005, 16(3): 645-678.
[2] Toivonen H, Klemettinen M, Ronkainen P, et al. Pruning and grouping discovered association rules[J]. Anesthesiology, 2008, 73(3A):971-975.
[3] Strehl A,Gupta G K,Ghosh J. Distance based clustering of association rules[C]. St Louis, Missouri:Proc of Intelligent Engineering Systems Through Artificial Neural Networks, 1999:759-764.
[4] Chen G Q, Wei Q. Fuzzy association rules and the extended mining algorithms[J].Information Sciences, 2002,147:201-228.
[5] 阮备军,朱扬勇.基于商品分类信息的关联规则聚类[J].计算机研究与发展,2004,41(2):352-360.
[6] 沈斌,姚敏,刘艳彬.基于带语义差别的模糊Taxonomy的交易数据库关联规则聚类[J].情报学报,2010,29(2):246-253.
[7] 刘军伟.钢铁工业泛在信息匹配推送服务体系及其实现方法研究[D]. 武汉:武汉科技大学,2015.
[8] 陈安,陈宁,周龙骧,等.数据挖掘技术及应用[M].北京:科学出版社,2006:203,221.
[9] Goldberg A V. An efficient implementation of a scaling minimum-cost flow algorithm[J]. Journal of Algorithms, 1997, 22:1-29.
[责任编辑 郑淑芳]
Fuzzy classification of defect data association rules based on attribute differences
LiYi,KongJianyi,WangXingdong,LiuJunwei
(College of Machinery and Automation, Wuhan University of Science and Technology, Wuhan 430081,China)
In light of the fact that the association rules for defect data produced in the industrial process cannot be effectively organized after data mining, this paper proposes a fuzzy method for classification of defect data association rules on the basis of project attribute differences. Based on the fuzzy structure tree, the distance between the association rules is calculated, and the result is analyzed by the method of self-organizing neural network clustering. The proposed method is applied to the clustering analysis of data mining on the surface defects of cold rolled strip. The results show that the proposed method can not only obtain the correlation between two different attribute items but also find the distance between the defect association rules. The closer the distance association rules that are grouped into one class, the more similar they are.
cold rolled strip; product defect; attribute; association rule; fuzzy classification; distance; cluster analysis; visualization
2016-09-06
国家自然科学基金面上项目(51174151);湖北省重大科技创新计划项目(2013AAA011);湖北省自然科学基金资助项目(2013CFA131).
李 怡(1991-),男,武汉科技大学硕士生.E-mail:yilee1991@qq.com
孔建益(1961-),男,武汉科技大学教授,博士生导师.E-mail:kongjianyi@wust.edu.cn
10.3969/j.issn.1674-3644.2017.01.010
TH164
A
1674-3644(2017)01-0049-06

