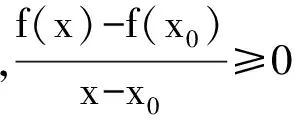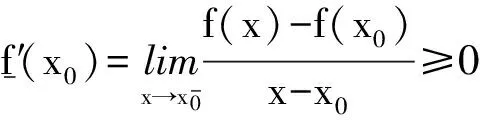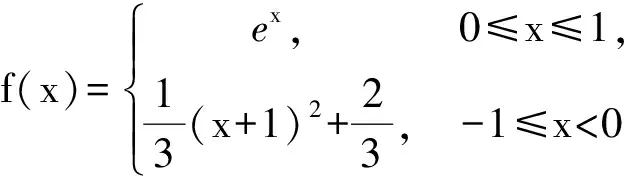关于凸性的一些探讨
廖俊俊, 吴 洁
(华中科技大学数学与统计学院,武汉430074)
关于凸性的一些探讨
廖俊俊, 吴 洁
(华中科技大学数学与统计学院,武汉430074)
现行的不少教材在叙述凸函数定义时,通常都假设函数是连续的.本文以没有连续为前提的一元凸函数的定义为基础,探讨了函数的连续性,左右导数的存在性,凸函数在区间端点的形态,最后利用左右导数,给出了判定函数为凸的一个充要条件.
连续性; 凸函数; 左导数; 右导数
1 引 言
在第二届全国大学生数学竞赛(数学类,预赛)中有如下试题:
注 函数f(x,y)是凸函数的定义是∀α∈(0,1)以及(x1,y1),(x2y2)∈D,成立
f(αx1+(1-α)x2,αy1+(1-α)y2)≤αf(x1,y1)+(1-α)f(x2,y2).
答案是肯定的.需要说明的是,这里所说的凸函数(convex function),在现行的有些教材中称为下凸函数.
上述试题引起了我们的思考,原因是现行的不少教材在叙述凸函数的定义时,通常都假设函数是连续的[1-4],即便有的教材叙述凸函数的定义时没有连续这一条件[5-7],也并没有以此为基础讨论函数的分析性质.最近的文[8],也仅讨论了凸函数单侧导数的连续性.本文以没有连续为前提的一元凸函数定义为基础,探讨了函数的连续性,左右导数的存在性,凸函数在区间端点的形态,最后利用左右导数,给出判别凸函数的一个充要条件.
2 凸函数的定义及连续性
定义1[7]设函数f在闭区间[a,b]上有定义,若∀α∈(0,1)以及∀x1,x2∈[a,b],成立
f(αx1+(1-α)x2)≤αf(x1)+(1-α)f(x2) ,
(1)
则称函数f在[a,b]上是凸函数.
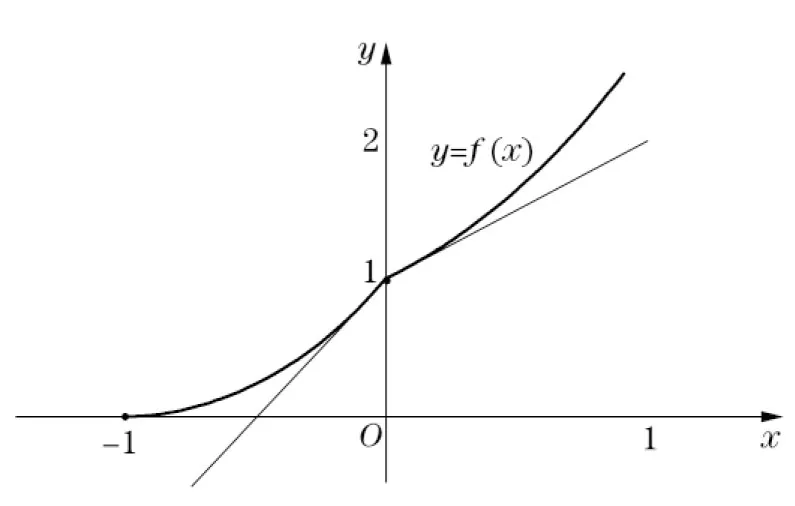
式(1)等价于对任意的a≤x1 (2) 也等价于 (3) 在几何上等价于任意两点(x1,f(x1))和(x2,f(x2))之间的弧位于这两点连线的下方. 若将[a,b]换成(a,b),则得到相应的开区间内的凸函数定义. 下述定理1将告诉我们,凸函数在开区间内每一点都存在左导数与右导数. 定理1设函数f是闭区间[a,b]上的凸函数,则对任意x∈(a,b),f(x)的右导数f′+(x)、左导数f′-(x)均存在;且f′-(x)≤f′+(x). 证对任意x∈(a,b),令 任取充分小的h1,h2>0,使得x 于是 这就证明了f(x)的右导数f′+(x)存在,类似可证明f(x)的左导数f′-(x)存在. 注意到∀x∈(a,b)以及足够小的h1,h2>0,若a 分别令h1→0+,h2→0+,即得f′-(x)≤f′+(x). 由定理1即可得到下面关于连续性的结论. 定理2设函数f是闭区间[a,b]上的凸函数,则函数f在开区间(a,b)内连续. 证对任意x∈(a,b),因 故f在(a,b)内左连续.类似可得f在(a,b)内右连续,从而f在(a,b)内连续. 注 尽管当函数f是闭区间[a,b]上的凸函数时,能得到f在开区间(a,b)内连续,但f在端点a及b上并不一定是单侧连续. 图1 f(x)图像如图1所示.由图像可知,f是[-1,1]上的凸函数,且在(-1,1)内连续,但f在x=-1以及x=1点均不单侧连续. 例1表明,闭区间[a,b]上的凸函数f可能在端点a或b处不连续.我们自然会问:对于一个闭区间上的凸函数,当它在端点不连续时,其在端点附近的形态如何?下面的定理回答了这个问题. 定理3设函数f是闭区间[a,b]上的凸函数,则函数f在端点a和b单侧极限都存在,并且f(a+)≤f(a),f(b-)≤f(b). 证仅证f(a+)≤f(a)(f(b-)≤f(b)可类似证明).对任意x∈(a,b),f是闭区间[a,b]上的凸函数,由凸函数定义得 (4) 所以|f(x)|≤|f(a)|+|f(b)|,即函数f在[a,b]上有界.任意a 即有 固定c1,c,上式两边令x→a+并取下极限,得 上述结论告诉我们,尽管闭区间上的凸函数在端点可能不连续,但形态也相当好——具有单侧极限. 对于一个开区间内的凸函数,它在区间端点附近又会是什么样的表现呢?请看定理4. 定理4设函数f是(a,b)内的凸函数,则 (i)对于端点a,要么f(a+)存在,要么f(a+)=+∞; (ii)对于端点b,要么f(b-)存在,要么f(b-)=+∞. 证(i)任取a 由此,得到 (ii)的证明与(i)类似. 经试验数据的对比,计算验证系统测量值与4种不同位姿检测方法的误差绝对值,误差绝对值变化趋势如图10所示。 最后,用单侧导数导出一个函数为凸函数的充要条件.为此,先证明Fermat定理的一个推广. 引理1设(a,b)内的函数f在点x0∈(a,b)的左、右导数都存在,且f′-(x0)≤f′+(x0).如果x0为f的一个极大值点,那么f在x0点可导,且有f′(x0)=0. 从而 f′-(x0)≥0≥f′+(x0).而另一方面,根据条件有f′-(x0)≤f′+(x0),因此 f′-(x0)=f′+(x0)=0. 即f在x0点可导,且有f′(x0)=0. 注 容易知道,对于极小值点也有与引理1对偶的结论. 定理5函数f是闭区间[a,b]上的凸函数的充要条件是f在开区间(a,b)内任一点的左、右导数都存在,以及在端点a,b处对应的单侧极限存在,且满足 (ii)f(a+)≤f(a),f(b-)≤f(b). 证必要性.由定理1知f在(a,b)内任一点的左右导数都存在,再由定理3可知f在端点a和b处相应的单侧极限都存在,并且f(a+)≤f(a),f(b-)≤f(b).即得(ii)成立. 对任意a 分别令x1→x-,x2→x+,y1→y-,y2→y+,得f′-(x)≤f′+(x)≤f′-(y)≤f′+(y),即(i)成立. 充分性.首先对任意x∈(a,b),函数在x点的左右导数都存在,故函数在(a,b)内连续;其次,因为在端点的单侧极限存在以及条件(ii),所以不妨假设f(a+)=f(a),f(b-)=f(b).对任意a≤x1 显然g是连续函数,且对x1≤x≤y≤x2,有 g′-(x)≤g′+(x)≤g′-(y)≤g′+(y). (5) 由凸函数定义的式(3)形式知,只需证对x1≤x≤x2,g(x)≤0. 利用定理5,可以很容易地判断一个分段函数是否为凸函数. 解易知函数f在[-1,0]以及[0,1]上都是凸的.由于 故由定理5知函数f在区间[-1,1]上是凸的(如图2所示). 解易知函数g(x)在[-1,0]以及[0,1]上都是凸的.但由于 由定理5,可知函数g(x)在区间[-1,1]上不是凸的(如图3所示). 图2 图3 [1] 王绵森 马知恩.高等数学基础 一元函数微积分与无穷级数[M].2版.北京:高等教育出版社,2010:142. [2] 同济大学数学系.高等数学:上册[M].6版.北京:高等教育出版社,2007:149. [3] 上海交通大学数学系微积分课程组.大学数学微积分:上册[M].北京:高等教育出版社,2008:175. [4] 复旦大学数学系.数学分析:上册[M].2版.北京:高等教育出版社,1983:204. [5] 韩云瑞,扈志明,张广远.微积分教程:上册 [M].2版.北京:清华大学出版社.2006:184. [6] 华中科技大学数学系.微积分学:上册[M].3版.北京:高等教育出版社,2008:137. [7] 华东师范大学数学系.数学分析:上册[M].4版.北京:高等教育出版社,2010:151. [8] 张亚楠,刘长剑.关于凸函数单侧导数的连续性[J].大学数学,2015,31(4):53-54. Some Researchs on the Convexity LIAOJun-jun,WUJie (School of Math.and Statistic,Huazhong University of Science and Technology,Wuhan 430074, China) The convex function often plays an important role in many fields of mathematics.It is meaningful to study the analytical properties of the convex function.In these paper, the continuity of the convex function has been studied.The limit property of the convex function about the end points of the interval has been discussed.A criteria of convex function has been given. continuous function; convex function; left derivative; right derivative 2016-05-13; [修改日期] 2016-06-20 华中科技大学2015年教学研究项目(2015068) 廖俊俊(1973-),男,博士,讲师,从事随机分析、泛函分析研究.Email:liaojunjun@hust.edu.cn 吴洁(1962-),女,硕士,教授,主要从事微积分教学与研究.Email:wujie627415@163.com O172.1 C 1672-1454(2016)06-0091-05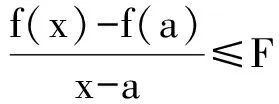




3 区间端点附近的性态探讨
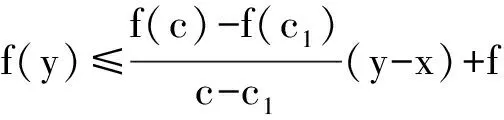

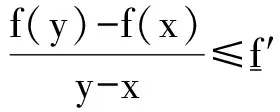




4 凸函数的单侧导数判别定理