基于Lasso和支持向量机的粮食价格预测

喻胜华，龚尚花

(湖南大学 经济与贸易学院，湖南，长沙 410079)

基于Lasso和支持向量机的粮食价格预测

喻胜华，龚尚花

(湖南大学 经济与贸易学院，湖南，长沙 410079)

首先利用Lasso方法在影响粮食价格波动的众多因素中选出了粮食储备、粮食生产成本、粮食产量、粮食政策、生产需求、贸易需求、心理预期等7个主要影响因素；然后在Lasso变量选择的基础上利用支持向量机进行粮食价格的回归与预测，同时，把Lasso、支持向量机、Lasso-支持向量机及ARIMA方法的拟合预测效果进行比较。实证结果表明：Lasso-支持向量机组合预测方法的拟合预测效果要优于另外三种预测方法。

粮食价格预测；影响因素；Lasso；支持向量机

一 引言及文献综述

粮食作为一种基础产品,其价格的波动会对我国粮食生产、粮食相关产品的进出口以及国家宏观经济调控产生深远影响,关系到消费者和生产者的切身利益。深刻了解和剖析影响粮食价格波动的各种因素,在此基础上建立相关的预测模型分析和预测粮食价格的变化趋势,有助于有关职能部门调控粮食价格并制定相应的措施,从而正确引导粮食市场的健康运行、保障粮食产品的供求平衡。

目前，国内外关于粮食价格预测研究的方法主要有定性和定量两大类，在定性分析方面，朱险峰[1]所做的系列价格预测研究比较有代表性,他通过分析库存、产量、国际市场上粮食价格的变动等一些影响因素,研究我国粮食价格的波动趋势，进而预测粮食的现货价格和期货价格。在定量分析方面，主要采用的是普通时间序列分析方法,其中最具代表性的是ARIMA方法，姚霞等[2]利用ARIMA模型并以青椒价格为例预测了时鲜农产品价格的动态变化；桂文林等[3]采用X-12-ARIMA模型分解我国粮食消费价格月度定基指数,得到了趋势循环、季节和不规则因素,进而分析了粮食价格的季节特征及其深层成因；陈兆荣等[4]利用ARIMA-SVM组合模型并结合1999～2011年我国农产品价格指数月度数据对我国农产品价格进行了预测。其他时间序列方法也有所应用，如苗开超[5]运用指数平滑模型对农产品价格进行了预测；刘家富等[6]利用向量自回归模型分析了国内大豆以及豆油市场的价格传导机制。除此之外，神经网络和支持向量机等方法也得到了不同程度的应用，如彭琳等[7]利用NARX神经网络方法对云南省的农产品价格进行了预测；孙超等[8]分析了我国粮食价格波动的主要影响因素,并利用支持向量机(SVM)方法建立了我国粮食价格的预测模型。支持向量机是基于结构风险最小化原则提出来的一种统计学习方法，该方法一改传统方法的经验风险最小化原则，从而使其有更好的泛化能力，尤其是较好地解决了小样本、非线性、过拟合和局部极小等几类常见的问题。我们知道，粮食价格数据是典型的小样本数据，而且，影响粮食价格的众多因素之间也存在着不确定性和非线性的关系，所以可以采用支持向量机方法进行预测，但是影响粮食价格的因素很多，各个影响因素之间可能会存在严重的多重共线性，如果不加选择地引入众多影响因素来进行粮食价格的预测，往往不能取得良好的预测效果。一个理想的模型应该是既不遗漏重要的自变量，也不包含没有影响或影响很小的自变量，过多地引入变量不仅会大大增加计算量，也会降低估计和预测精度。

虽然支持向量机方法比较适合处理具有非线性关系的小样本数据，但是不能进行变量选择，而Lasso方法可以同时进行参数估计和变量选择，Lasso方法本质上还是线性回归方法，它不适合处理非线性问题，所以，本文提出了基于Lasso与支持向量机的粮食价格组合预测方法。首先利用Lasso方法对粮食价格波动的影响因素进行选择，剔除与粮食价格不相关或相关性很小的变量数据，以达到降低数据维数的目的；然后利用支持向量机的非线性运算能力，逼近历史数据所隐含的函数关系，完成对粮食价格的拟合和预测，同时，把Lasso、SVM、Lasso-SVM及ARIMA方法的拟合预测效果进行比较。

二 Lasso及支持向量机方法

1. Lasso方法

Lasso方法(最小绝对值压缩与选择方法)是Tibshirani.R[9]在1996年提出来的一种的有偏估计方法，其本质是通过添加约束条件对模型系数进行压缩，将没有影响或影响较小的自变量的回归系数自动压缩到零，这不仅在一定程度上能消除多重共线性的影响，而且在对参数进行估计的同时也实现了对变量的选择。

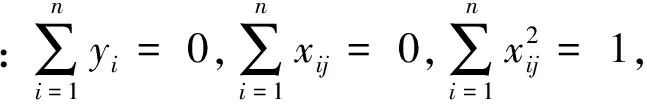
对于线性模型：

y=α+β1x1+β2x2+…+βpxp+ε，

常数项和回归系数的Lasso估计定义为：

我们可以用二次规划方法求回归系数的Lasso解，但计算量很大，直到2004年，Efron,B等[10]提出的最小角回归算法才很好地解决了Lasso方法的计算问题，也使得该方法在生物学和化学等众多领域得到了广泛的应用。与逐步回归、最优子集选择、岭回归、主成分回归、偏最小二乘回归、投影寻踪以及刀切法等传统的变量选择方法相比，Lasso方法具有预测精度高、模型的可解释性强以及计算比较简单等优点。

2. 支持向量机方法

支持向量机(SVM)[11-12]是一种专门解决小样本统计学习规律的方法，它的核心是引入核映射的思想与结构风险的概念。目前，该方法已经广泛应用于经济研究领域，其主要原理如下：

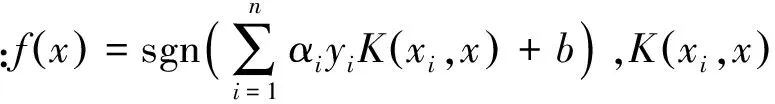
(2)多项式核函数：

(3)径向基核函数(RBF)：

(4)两层感知器核函数(Sigmoid)：

三 建模与实证分析

1. 数据来源及变量选择

根据经济学理论及已有的研究结论，我们从粮食储备、粮食生产成本、粮食产量、粮食政策、生活需求、生产需求、贸易需求、心理预期以及外部冲击等9个方面共选取了21个变量[13-16]。具体如下：用粮食类零售价格指数代表粮食价格；用粮食库存量x1、期末库存消费比x2反映粮食储备；用粮食生产价格指数x3反映粮食生产成本；用总产量x4、 粮食作物播种面积x5、成灾面积x6反映粮食产量；用农业支出x7、农业支出占财政支出的比重x8反映粮食政策；用城镇居民人均可支配收入x9、农村居民家庭人均纯收入x10、城镇居民人均粮食消费x11、农村居民人均粮食消费x12反映生活需求；用农业生产资料价格指数x13、国内生产总值指数x14、世界能源价格指数x15反映生产需求；用粮食净进口x16、人民币对美元汇率x17反映贸易需求；用上一期真实粮价增长率x18、货币和准货币(M2)供应量x19反映心理预期；用同期通货膨胀率x20、世界谷物价格指数x21反映外部冲击。

本文选取的数据区间是1978-2013年，粮食库存量、期末库存消费比数据由作者根据美国农业部信息网提供的数据计算得出；粮食生产成本数据来自《全国农产品成本收益汇编》；世界谷物价格指数、世界能源价格指数数据来自世界银行数据库；农业支出、农业支出占财政支出的比重、城镇居民人均粮食消费、农村居民人均粮食消费数据来自中国农村统计年鉴；其他数据均来自《中国统计年鉴》。

2. 基于Lasso回归的变量选择

首先把数据进行中心标准化处理，以消除不同指标量纲的影响，接下来运用Lasso方法对选取的21个指标进行参数估计与变量选择，只需要29步，就可以得到全部的Lasso解。从图1可以看出，当参数s很小时，变量均未被选入模型中，随着s的不断增大，变量依次进入模型，当s=1时，变量全部进入模型。

图1 Lasso方法的变量选择路径

本文选择AIC准则确定最优解，根据Lasso回归的参数估计结果，在第14步时AIC达到最小值0.2454，这时模型最优，表1给出了第14步路径的模型系数的估计值，最终选取了x2，x3，x4，x5，x6，x8，x13，x15，x16，x17，x18，x20共12个变量，剔除了9个与粮食价格预测不相关或相关性很小的变量。

Lasso变量选择结果显示：粮食生产价格指数、粮食作物播种面积、农业生产资料价格指数、粮食净进口、人民币对美元汇率、同期通货膨胀率对提高粮食价格有显著的正向作用，期末库存消费比、粮食总产量、成灾面积、农业支出占财政支出的比重、能源价格指数、上一期真实粮价增长率对提高粮食价格有显著的负向作用，其中粮食生产价格指数、粮食作物播种面积、农业生产资料价格指数、人民币对美元汇率对粮食价格波动的影响远远大于其他因素的影响，说明国家在进行宏观调控和稳定粮食价格时可以主要从控制粮食生产成本、粮食作物播种面积、农业生产资料价格、人民币对美元汇率这四方面采取相应的措施。而粮食库存量、农业支出、城镇居民人均可支配收入、农村居民家庭人均纯收入、城镇居民人均粮食消费、农村居民人均粮食消费、国内生产总值指数、货币和准货币(M2)供应量、世界谷物价格指数对粮食价格波动的影响不显著，这些变量没有被选入模型。

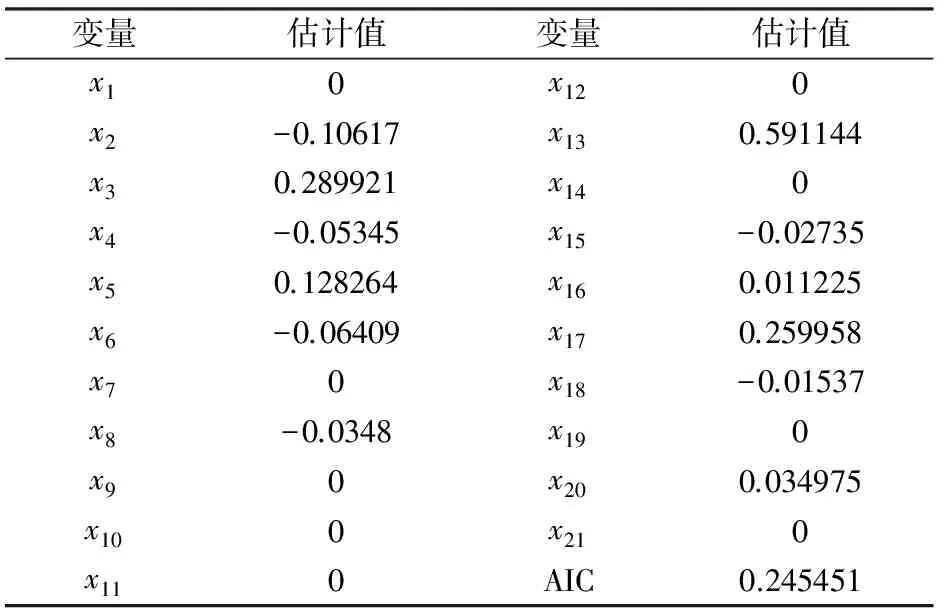
表1 Lasso方法在第14步时的参数估计结果

3.基于Lasso与支持向量机的粮食价格预测

根据上文的Lasso回归结果，选取x2，x3，x4，x5，x6，x8，x13，x15，x16，x17，x18，x20共12个变量作为全国粮食类零售价格指数Y的解释变量。在进行Lasso-SVM粮食价格预测模型的建立及预测的过程中，我们把1978～2009年的32个样本作为拟合训练样本，2010～2013年的4个样本作为预测检验样本。在进行模型训练与预测之前，首先利用FormatDatalibsvm.xls处理原始数据，使得数据格式符合libsvm-3.20的要求，然后进行数据的归一化处理，降低模型训练时数值计算的难度，提高预测精度。

核函数的选择会影响着支持向量机的回归性能的好坏，我们选择前文提到的四种常见的核函数分别构建支持向量机回归模型，实证结果表明：在预测粮食价格的支持向量机回归模型中，基于径向基核函数(RBF) 的支持向量机其性能优于基于其它核函数的支持向量机，所以本文选用径向基核函数。 另一方面，惩罚参数在很大程度上影响着支持向量机的泛化性能的好坏，本文选用交叉验证方法中的K-foldCrossValidation(K-CV)方法来确定参数，将训练数据分成10份做交叉验证，运用gridregression.py函数进行参数自动寻优，参数自动寻优结果为：bestc=1024.0， g= 0.0625，p= 0.5，MSE=1035.41。在确定了最优参数和核函数之后，就可以对预测粮食价格的支持向量机回归模型进行拟合训练，其拟合结果如图2所示。从图2可以看出，Lasso-SVM模型的拟合效果非常理想，拟合优度系数R2高达0.98，这是一个好的预测模型所必不可少的。

图2 Lasso-SVM训练拟合结果

接下来利用训练所得到的支持向量机回归模型对2010-2013年的粮食价格进行预测，为了考察粮食价格的预测效果，用平均绝对误差、平均绝对百分误差(MAPE)和均方根误差(RMSE)三个指标来测定预测的精度，数值越小表明预测值和真实值间的差异越小，预测精度越高。为了比较预测精度，另单独使用Lasso模型、SVM模型和传统应用最广泛的ARIMA模型对粮食类零售价格指数进行预测，四种模型的预测结果见表2，并计算四种模型的预测精度指标见表3。

表2 粮食类零售价格指数实际值与预测值比较

表3 四种模型的预测精度比较

从表2和表3的结果可以看出，Lasso-SVM模型的预测值与真实值的趋势基本一致，误差较小，平均相对误差率仅2.233%，预测效果比较理想，Lasso-SVM模型能够很好地反映粮食价格与其影响因素之间复杂的非线性关系。从比较四个预测模型的预测结果可以看出： 第一、基于粮食价格波动的影响因素所建立的Lasso模型、SVM模型和Lasso-SVM模型都比直接使用粮食价格时间序列数据的ARIMA模型的预测效果好，这表明本文建立的指标体系是有效的，深入剖析粮食价格波动的影响因素能更好地对粮食价格作出预测；第二、非线性的SVM模型和Lasso-SVM模型比线性的Lasso模型和ARIMA模型的预测效果要好，这是因为粮食价格时间序列数据往往更多地表现为非线性且含有复杂的噪声，所以用非线性模型进行预测能取得更好的预测效果； 第三、Lasso-SVM模型的预测精度都要高于普通SVM模型和Lasso模型，这可以说明：在粮食价格预测问题上，使用Lasso方法进行变量选择之后再运用支持向量机方法进行预测有一定的优势，能够提高预测精度，拥有更好的预测性能。

四 结语

由于粮食价格的影响因素众多，而且处于不断动态变化中，本文首先在学者已有研究结论和相关经济学理论的基础上，深入剖析了中国粮价波动的主要因素。考虑到在众多影响因素当中存在着很多对粮食价格波动影响甚微的因素，我们创新性地将Lasso回归作为一种变量选择方法引入到粮食价格预测中来，在该方法之下，我们删除了系数估计值为零的9个变量，仅保留了粮食生产价格、粮食作物播种面积、农业生产资料的价格、人民币对美元汇率等12个对粮食价格波动影响较大的因素。其中，前4个因素对粮食价格波动的影响程度要远远大于其他8个因素，说明国家或地方政府在调节粮食价格时应该重点从这几个方面着力。同时，运用SVM回归算法对经过Lasso方法处理后的变量数据集进行粮食价格预测，并通过与Lasso模型、SVM模型和传统的时间序列ARIMA模型的预测结果进行对比，验证了Lasso-SVM模型的有效性和优越性。从预测的精度来看：Lasso-SVM模型要优于Lasso模型、SVM模型和ARIMA模型，它能较好地反映粮食价格与各主要影响因素之间的非线性关系。可以预期：Lasso-SVM方法在工农业、经济管理、医药卫生、气象地质以及教育心理等众多实际领域会有良好的应用前景。

[1] 朱险峰.国际市场粮价演变与国内粮价关系分析[J].农业展望, 2007，(9): 3-7.

[2] 姚霞，彭汉艮，朱艳，曹卫星，张卫建.时鲜农产品价格预测的ARIMA时序模型构建与应用[J].农业系统科学与综合研究,2007，(1)：89-94.

[3] 桂文林，韩兆洲.基于X-12-ARIMA模型的中国粮食消费价格运行[J].华东经济管理,2011，(3): 61-67.

[4] 陈兆荣，雷勋平，王亮，叶松.基于ARIMA-SVM组合模型的我国农产品价格预测研究[J].财经理论研究，2013，(2):103-107.

[5] 苗开超.基于指数平滑模型的农产品价格预测研究[D]. 合肥工业大学，2009.

[6] 刘家富，李秉龙，李孝忠.基于VAR模型的国家大豆和豆油市场价格传导研究[J].农业技术经济,2010，(8):33-38.

[7] 彭琳，林明.基于NARX神经网络的农产品价格时间序列预测方法研究[J].农机化研究,2013，(11):18-21.

[8] 孙超,孟军.中国粮食价格的影响因素分析与预测比较----基于支持向量机的实证研究[J].农业经济,2011，(1):29-31.

[9]Tibshirani,R.RegressionShrinkageandSelectionViatheLasso[J].JournaloftheRoyalStatisticalSociety,1996,(58):267-288.

[10]Efron,B.,Hastie,T.Johnstone,I.andTibshirani,R.LeastAngleRegression[J].Ann.Statist.,2004，(32):407-499.

[11]Vapnik，V.TheNatureofStatisticalLearningTheory(SecondEdition) [M].NewYork:SpringerVerlag, 1999：225-260.

[12] 孙德山.支持向量机分类与回归方法研究[D].中南大学，2004.

[13] 王淑艳.我国粮食价格波动因素分析与预测研究[D].东北农业大学，经济管理学院，2013.

[14] 王川.我国粮食市场价格的影响因素分析[J].农业经济，2010,(7):24-27.

[15] 罗锋,牛宝俊.我国粮食价格波动的主要影响因素与影响程度[J].华南农业大学学报(社会科学版),2010,(2):51-58.

[16] 马林林,金彦平,张安良.我国粮食价格波动影响因素探析[J].价格理论与实践,2011,(10):23-24.

A Study on Grain Price Prediction Based on Lasso and Support Vector Machine

YU Sheng-hua,GONG Shang-hua

(School of Economics and Trade,Hunan University,Changsha 410079,China)

The paper firstly chooses grain reserves, grain production cost, grain production, grain policy, production demand, trade demand, and psychological expectations as seven main factors influencing grain price volatility based on the Lasso method. And then, according to Lasso variable selection, we conduct the regression and forecasting of grain prices with the help of support vector machine (SVM). At the same time, by comparing the fitting prediction effect of the Lasso, support vector machine (SVM), Lasso-SVM and ARIMA method, the empirical results show that the Lasso-SVM of fitting forecasting effect considerably overmatches the other three methods.

grain price prediction; influencing factors; Lasso; support vector machine

2015-04-08

国家社会科学基金资助项目 “复杂数据建模中组合预测方法及应用研究”(12BTJ014)；湖南省哲学社会科学基金项目(14YBA092)

喻胜华(1966—)，男，湖南宁乡人，湖南大学经济与贸易学院教授，博士生导师，博士. 研究方向：数量经济学.

F069

A

1008—1763(2016)01—0071—05