土的特性与支锚位置对支锚式挡墙嵌固深度的影响

韦人伟,杨瑞敏

(1.安徽安德建筑设计有限公司，安徽 合肥 230000;2.安徽科技学院,安徽 凤阳 233100)

土的特性与支锚位置对支锚式挡墙嵌固深度的影响

韦人伟1,杨瑞敏2

(1.安徽安德建筑设计有限公司，安徽 合肥 230000;2.安徽科技学院,安徽 凤阳 233100)

目的：研究基坑开挖深度、土的重度、内摩擦角、外加荷载与支锚位置等对支锚式挡土墙嵌固深度的影响，为非粘性土中支锚式及悬臂式挡土墙的设计提供理论依据。方法:提出一个支锚式挡土墙的计算模型，通过对模型进行合理的简化和控制变量法，计算分析土体特性与支锚位置对挡土墙嵌固深度的影响。结果:挡土墙嵌固深度与土的重度无关，随着外加荷载和挡土墙高度的增加呈线性增加，随着土体内摩擦角的增加呈非线性减少，支锚位置对挡墙嵌固深度的影响也较大。结论:随着支锚发挥作用，所需挡墙的最小嵌固深度减少超过50%，从开挖深度4/5位置以上向下移动支锚，所需挡墙的嵌固深度随之减少，最佳支锚位置在基坑开挖深度的3/4位置处。

挡土墙设计；嵌固深度；土的特征；支锚的作用；最佳支锚位置

挡土墙能够起到阻止墙后土体滑坍、保护路基及收缩边坡的作用，在房屋建筑、桥梁、道路及水利工程中应用广泛。挡土墙的设计中，挡墙结构及构造的选择、土压力的计算、抗倾覆与抗滑移破坏的验算均尤为关键[1-4]。悬臂式、扶壁式、错杆式和加筋土式挡土墙等柔性支挡结构的设计中，挡墙最小嵌固深度的确定是支锚式挡土墙设计的关键[5-6]。目前国内外挡土墙设计的研究，主要集中于探讨挡土墙的破坏机制、挡土墙设计的简化模型及挡土墙稳定性验算安全系数等问题[7-8]。本文主要研究土的特性和支锚对挡土墙设计的影响，尤其是支锚位置对支锚式挡土墙嵌固深度的影响。

1 原理与方法

1.1 无支锚式挡土墙中嵌固深度计算

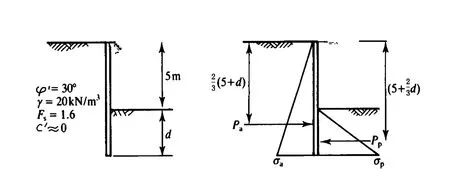
图1 无支锚式挡土墙中的土压力

(1)朗肯主动土压力系数Ka和朗肯被动土压力系数Kp计算：

(1)

(2)

(2)主动土压力Pa和被动土压力Pp计算：

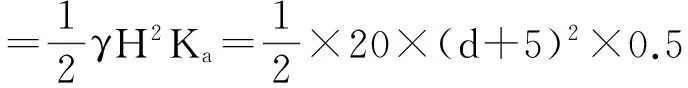
(3)

(4)

图1所示为挡土墙中受力情况、主动土压力和被动土压力的分布，根据力矩平衡法则∑M0=0即Mpa-Mpp= 0，对挡土墙顶部求合力矩可得：

(5)

由式(5)可得挡土墙的嵌固深度。为了分析支锚的影响，首先不放置支锚对挡土墙中嵌固深度进行计算，用控制变量的方法分析基坑开挖深度、内摩擦角、土体重度，外加荷载对嵌固深度的影响。第Ⅰ组试验研究的是基坑开挖深度对嵌固深度的影响，根据控制变量法，在这组试验中保持内摩擦角、土体重度、外加荷载不变、分别假设基坑开挖深度为5 m、10 m、15 m、20 m、25 m、30 m、35 m、40 m,按照上述计算方法求不同基坑开挖深度的嵌固深度。

(6)

(7)

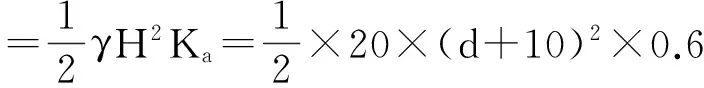
(8)

(9)

同理，挡墙两侧土压力分别对挡土墙顶部求力矩，可求得嵌固深度。第Ⅱ组试验保持基坑开挖深度、土体重度、外加荷载不变，分别增加内摩擦角到25°，35°，40°，45°，分别求得嵌固深度。

1.1.3 土体重度对嵌固深度的影响 假设φ′=30°、基坑开挖深度为10 m，改变土体重度，可得挡土墙中主被动土压力(见式10～11)，其中Ka=0.5，Kp=2.0分别为主动、被动土压力系数。

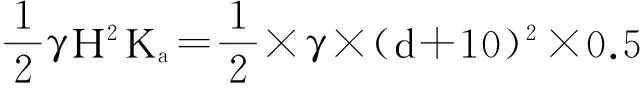
(10)

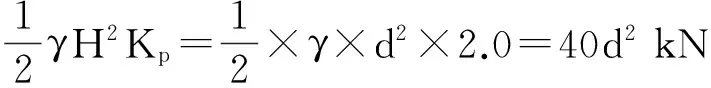
(11)

第Ⅲ组试验保持基坑开挖深度、内摩擦角、外加荷载不变，增加土体重度至10 kN/m3、15 kN/m3、20kN/m2、25 kN/m3、30 kN/m3，分别求得嵌固深度。

1.1.4 外加荷载对嵌固深度的影响 假设φ′=30°以及基坑开挖深度H =10 m 并将土体重度调整为γ=20 kN/m3,在挡土墙顶部布置均布荷载q=10 KN/m。考虑到新增的外加荷载作用，需要对挡土墙中内力进行重新分析，可得挡墙的嵌固深度如下表1所示。

表1 无支锚嵌入式挡土墙在外加荷载为10 KN/m时嵌固深度的计算

根据力矩平衡条件，由Mpa+Mpp-Mpp=0可得挡墙嵌固深度。第Ⅳ组试验中将外加荷载q逐步增加，由q=10 KN/m增加到20 KN/m，30 KN/m，40 KN/m，50 KN/m，通过计算可得到不同的嵌固深度。

1.2 支锚嵌入式挡土墙中嵌固深度的计算

挡土墙设计中常采用无固定端支撑法假设，当主动土压力和被动土压力增加到一定程度时，挡土墙将发生滑移，可假设由底部B处滑移产生的挡土墙内土压力分布，如图2所示。

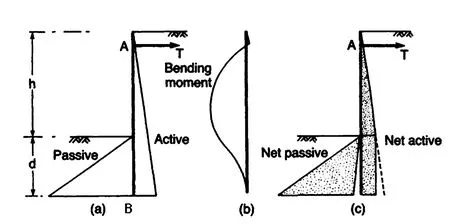
图2 无固定端支撑法在支锚嵌入式挡土墙中设计中

有支锚嵌入式挡土墙中嵌固深度的计算将基于以上的原理，在无支锚嵌入式挡土墙中嵌固深度的计算基础上，引入支锚进一步研究，新的挡土墙计算模型及内部土压力分布如图3所示：

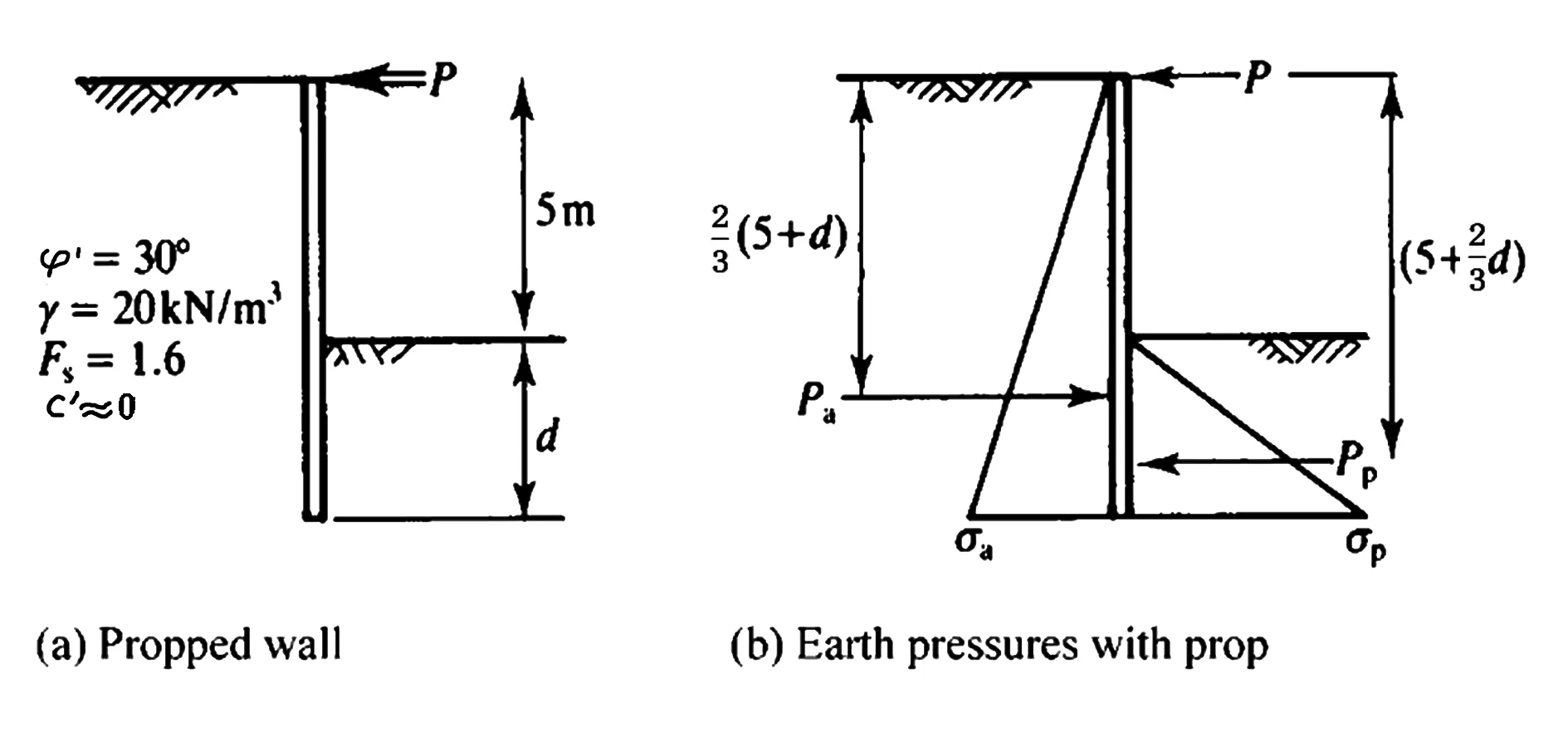
图3 支锚嵌入式挡土墙中的土压力

首先，将支锚放置于地平线等高处，即dp=0m，对插入点处受力分析并列出力矩平衡方程，可得挡墙的嵌固深度如下表2所示。

表2 基坑开挖深度为5m支锚距地面0.5m时嵌固深度的计算

Mpa-Mpp=0

(12)

(13)

将支锚下移，使dp=1.5 m，dp=2 m，dp=2.5 m，dp= 3 m=3.5 m，dp=4 m，dp=4.5 m，dp=5 m，通过计算可得相应的嵌固深度。当计算到dp=5 m时发现结果并不可用。因此从dp= 4 m处周围进一步进行试验，分别将支锚放置在距离地平面3.8 m以及3.9 m处，便可得到更加精确的数据。为了防止计算出现的偶然性对结果的影响，增加两组试验分别将基坑开挖深度增加到10 m以及15 m，并同样将支锚安置在地平面处开始并逐渐下移求得最佳嵌固深度。

2 结果与分析

2.1 基坑开挖深度、内摩擦角、外加荷载等对无支锚挡土墙嵌固深度的影响

基于1.1节提出的方法可计算不同开挖深度时内摩擦角、外加荷载、土体重度对嵌固深度的影响：(1)取不同开挖深度5 m、10 m、15 m、20 m、25 m、30 m、35 m、40 m进行计算可知，嵌固深度随开挖深度的增大而线性增大；(2)取不同的内摩擦角25°、35°、40°、45°进行计算可知，嵌固深度随土体摩擦角的增大而非线性减小；(3)取不同的附加荷载10 KN/m、20 KN/m、30 KN/m、40 KN/m、50 KN/m进行计算可知，嵌固深度随附加荷载的增大而线性增大；(4)取不同的土体重度10 KN/m3、15 KN/m3、20 KN/m3、25 KN/m3、30 KN/m3计算可知，嵌固深度与土体重度无关。

由上述计算结果可知，嵌固深度与基坑开挖深度呈线性正相关关系；当内摩擦角在一定范围内增加时，嵌固深度的值将减小；嵌固深度和外加荷载亦呈正相关关系，但不如基坑开挖深度对嵌固深度影响明显；嵌固深度不随土体重度的改变而改变，其原因在于在计算所列平衡方程中主动土压力Pa和被动土压力Pp都包含土体重度 ，当土体重度改变时，主被动土压力将同步改变，所以图中显示为一条直线。

2.2 支锚插入深度对嵌固深度的影响

为分析支锚插入深度对挡墙嵌固深度的影响，分别取开挖深度5 m、10 m、15 m时不同支锚插入深度进行计算：(1)开挖深度5 m时分别取支锚插入深度1 m、2 m、3 m和4 m计算可知，随着支锚插入深度的增加，所需挡墙嵌固深度逐渐减小，当支锚插入深度超过4 m后，挡墙的嵌固作用很小；(2)当开挖深度为10 m、15 m时，支锚插入深度分别超过8 m、12 m后，挡墙的嵌固作用很小，主要由支锚承担荷载。

由上述计算结果可知，当支锚插入时嵌固深度将明显减少，支锚沿着地平面下移时，嵌固深度也随之渐渐减少，直到距离地平面大约3.8m时出现陡降并产生负值，可能意味着挡土墙破坏的发生；当基坑开挖深度为10 m时的嵌固深度变化，同样出现趋势基本与基坑开挖深度为5 m时保持一致；当基坑开挖深度为15 m时的嵌固深度变化，除了趋势与之前保持一致之外，在11.5 m处出现破坏。经过比较发现，破坏都大约发生在将支锚放置在距离地平面占整个基坑开挖深度的3/4处。所以，下边将进一步探究两者比值dp/H与嵌固深度的关系。

2.3 dp/H与嵌固深度的关系

综合考虑基坑开挖深度为5 m、10 m、15 m时dp/H与嵌固深度的关系可发现，三组实验都在 比值约3/4处，嵌固深度达到最小值，即所需插入深度值最低，可知将支锚安置在整个基坑开挖深度的3/4左右处是最合理的设计。

2.4 无支锚和有支锚嵌入式挡土墙嵌固深度比较

为了将无支锚和有支锚时挡土墙所需嵌固深度进行比较，通过计算可得表3。从表中可明显看出，有支锚的挡土墙中所需嵌固深度要比无支锚挡土墙中嵌固深度小得多。

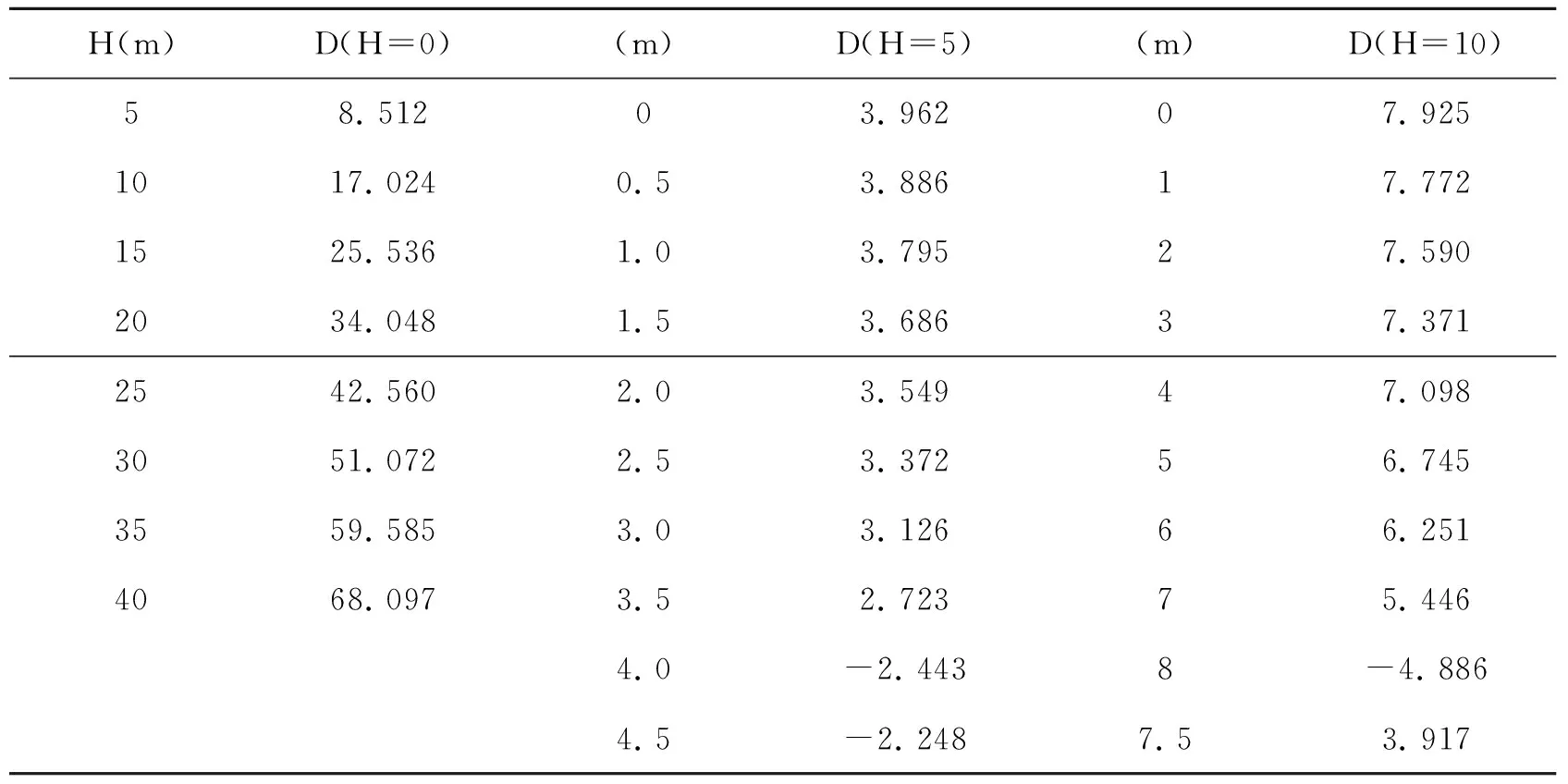
表3 无支锚和有支锚挡土墙所需嵌固深度的比较

3 结 论

提出一个支锚式挡土墙的计算模型，通过对模型进行合理的简化和控制变量法，计算分析土体特性与支锚位置对挡土墙嵌固深度的影响，主要得到如下结论：

(1)嵌固深度与土体重度无关，柔性支挡结构设计中无需考虑土重度对最小嵌固深度的影响；

(2)嵌固深度随着外加荷载和挡土墙高度的增加而线性增加，随着内摩擦角的增加而非线性减少，在合理范围内适当减小外加荷载和挡土墙高度和增加内摩擦角有利于优化设计；

(3)随着支锚发挥作用，所需的最小嵌固深度将减少一半以上，最大可减少80%，挡土墙高度较高时，选择柔性支挡结构更经济；

(4)受力分析发现最大弯矩发生在插入支锚附近处，且支锚的引入将造成挡土墙弯矩值的减少，从而降低挡土墙破坏的可能性；

(5)开挖深度4/5位置以上向下移动支锚，所需的嵌固深度将减少，最佳支锚位置在开挖深度的3/4位置处。

[1]Atkinson, J. The mechanics of soils and foundations[M]. Boca roton: CRC press, 2007: 101-111.

[2]Craig, F R. Craig's soil mechanics[M]. Boca roton: CRC press, 2012: 85-89.

[3]PADFIELD C J, MAIR R J. Design of retaining walls embedded in stiff clay[J]. Publication of Construction Industry Research, 1984(104): 11-18.

[4]Powrie, W. Soil mechanics:concepts and applications[M]. Boca roton: CRC press, 2013: 100-108.

[5]Salgado, R. The engineering of foundations[M]. New York: McGraw Hill, 2008: 669-713.

[6]Shubhra&Goel N.R.Patra Effect of Arching on Active Earth Pressure for Rigid Retaining Walls Considering Translation Mode[J.]Structure Congress，1994，8(3)：51-52．

[7]Smoltczyk, U. Geotechnical engineering handbook,elements and structures[M]. New York: John Wiley&Sons, 2003: 16-21.

[8] Symons I F, Kotera H. A Parametric Study of the Stability of Embedded Cantilever Retaining Walls[J]. Trrl Research Report, 1987: 87-93.

(责任编辑：李孟良)

The Influence of Soil Characteristics and Prop Location on the Required Penetration Depth of Embedded Retaining Walls

WEI Ren-wei1,YANG Rui-min2

(1.Ande Corporation of Architectural Designing of Anhui,Hefei 230000,China;2.Anhui Science and Technology University, Fengyang 233100,China)

Objective: This study is aimed at helping foster a comprehensive understanding of the influence of the prop location together with the retained height, value of surcharge and some soil characteristics on the penetration depth of embedded retaining walls, which will stand subsequent civil engineers in good stead by facilitating the decision-making process when designing cantilever or anchored retaining walls in granular soils. Methods: A simplified calculation model was created to stimulate the function of embedded retaining walls,to evaluate the effect of characteristics and prop location on the required penetration depth of embedded retaining walls respectively after the performing these detailed calculations. Results: Prodigious quantities of calculations plotted on graphs show that the required depth of embedment has nothing to do with γ(unit weight),increases linearly with q(surcharge) and h(height),and decreases non-linearly with friction angle. Conclusions: With a prop, the design depth of penetration will decrease by more than 50%.Additionally, the design depth of penetration decreases when you lower the prop before around 4/5 of the excavated depth measured from the ground level and the optimum prop level is about 3/4 of the retained height.

Design of retaining structures; Design penetration depth; Soil characteristics; Function of prop; Optimum prop location

2016-07-01

安徽科技学院人才引进项目(830158)。

韦人伟(1991-)，男，安徽省肥东县人，硕士，助理工程师，主要从事土木结构数值计算方面研究。

TU431

A

1673-8772(2016)06-0088-06