一类函数最值问题的探讨
◇ 陕西 徐建平
一类函数最值问题的探讨
◇ 陕西 徐建平
区间上二次函数的最值问题是初等数学中解决“恒成立”问题的重要基础之一.在长期的教学中,笔者深感此类问题是学生学习中的一个薄弱环节.现将此类问题归纳如下,愿与同行们商讨.
1 区间给定,对称轴确定
1)若对称轴在区间内,二次项系数为正时最小值在对称轴取得,最大值在区间端点取得,反之最大值在对称轴取得,最小值在区间端点取得.
例1求函数y=cos2x+2sinx的值域.
解析
y=cos2x+2sinx=-2sin2x+2sinx+1.设t=sinx,则-1≤t≤1,则原函数可化为y=-2t2+2t+1=-2(t-)2+,所以当t=时,ymax=3/2,当t=-1,ymin=-3,所以所求函数的值域为[-3,3/2].
例2(2013年全国新课标Ⅰ)若函数f(x)=(1-x2)(x2+ax+b)的图象关于x=-2对称,则f(x)的最大值为________.
解析
因为点(1,0)、(-1,0)在函数f(x)的图象上且图象关于直线x=-2对称,所以点


2)若所给区间位于对称轴的左侧或右侧,只须利用二次函数的单调性即可求出最值.
例3求的值域.
解析
该题的解法较多,本文只介绍转化为区间上二次函数求最值的方法.

2 区间给定,对称轴含参数
1)若二次函数的最大值、最小值均需求解时,应以区间的两端点和区间的中点为界点对参数分4种情况进行讨论.
例4求函数f(x)=x2-2ax-1,x∈[0,2]的值域.
解析
f(x)=x2-2ax-1=(x-a)2-a2-1.当a<0时,函数f(x)在[0,2]上单调递增,fmin(x)=f(0)=-1,fmax(x)=f(2)=3-4a.
当0≤a≤1时,fmin(x)=f(a)=-a2-1,fmax(x)=f(2)=3-4a.
当1<a≤2时,fmin(x)=f(a)=-a2-1,fmax(x)=f(0)=-1.
当a>2时,f(x)在[0,2]上单调递减,fmin(x)=f(2)=3-4a,fmax(x)=f(0)=-1.
综上,当a<0时,值域为[-1,3-4a];当0≤a≤1时,值域为[-a2-1,3-4a];当1<a≤2时,值域为[-a2-1,-1];当a>2时,值域为[3-4a,-1].
2)若只须求二次函数的最小值,应以区间的两端点为分界点对参数分3种情况进行讨论.

当λ>1,cosx=1时,fmin(x)=1-4λ,由题意知1-4λ=-,解得λ=,这与λ>1矛盾.
综上,λ=.
3)若只须求二次函数的最大值,应以区间的中点为分界点对参数分2种情况进行讨论.

(1)求a、b的值.
(2)若对t∈[0,2],不等式f(t2-2kt)+f(2t2-k)>0恒成立,求k的取值范围.
解析
(1)因为f(x)是奇函数,所以f(0)=0,f(-1)=-f(1),所以


又因为f(x)单调递减,所以t2-2kt<k-2t2,即对t∈[0,2],3t2-2kt-k<0恒成立.

解析
依题意可设P(0,1),Q(x,y),则

点Q在椭圆上,所以

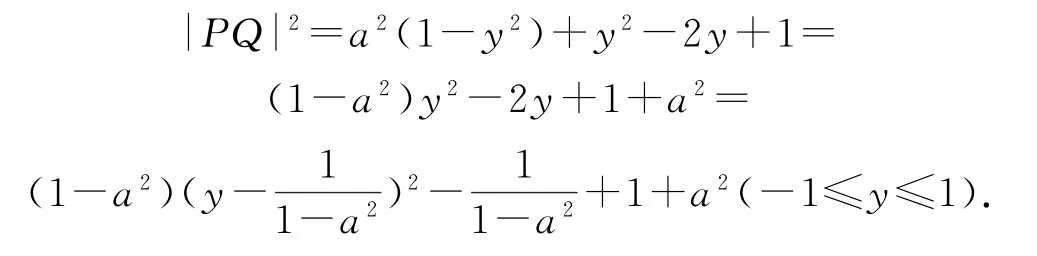
因为a>1,所以1-a2<0,本题转化为求开口向下的二次函数区间上最大值的问题.按常规思路应对以区间的两端点-1、1为界点分3种情况讨论.
由于a>1,所以,故只需对以-1为界点分2种情况讨论.

3 区间的端点含参数,对称轴确定
求区间端点含参数且对称轴确定情况下二次函数的最值,首先需明确题意要求,弄清楚是最大、最小值都需要求,还是只求最小值或最大值,然后根据情况,结合二次函数的图象,以区间的端点、中点位于对称轴的左、右进行讨论.
例8已知函数f(x)=x2-4x-4在闭区间[t,t+1](t∈R)上的最小值为g(t),试写出函数g(t)的表达式.
解析
f(x)=x2-4x-4=(x-2)2-8.
当t+1<2,即t<1时,f(x)在[t,t+1]上递减,g(t)=f(t+1)=t2-2t-7.

本文运用分类讨论思想对二次函数的最值问题进行了求解.解题中还应用了数形结合思想,即借助二次函数的图象,将所要解答的题目划归为本文所述某一类型问题进行求解.总之,熟练掌握二次函数的图形特征(对称轴、最值、单调性等)是求解其最值问题的一把利器.
(作者单位:陕西省西安市第八中学)

