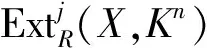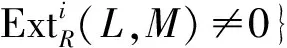(X,Y)-Gorenstein 同调维数

宋洁, 张春霞

(西北师范大学数学与统计学院, 甘肃 兰州 730070)

(X,Y)-Gorenstein 同调维数

宋洁, 张春霞

(西北师范大学数学与统计学院, 甘肃 兰州 730070)

研究(X,Y)-Gorenstein 投射与内射模的一些同调性质, 给出模的 (X,Y)-Gorenstein 投射与内射维数的等价刻画.

同调性质；(X,Y)-Gorenstein 投射(内射)模; (X,Y)-Gorenstein 投射(内射)维数

Gorenstein 同调代数的研究源于 Auslander 和 Bridger[1]的工作, 目前对这一领域的研究已取得了非常丰富的成果(参见文献 [2-6]). 称R-模M是Gorenstein投射模[2], 如果存在投射R-模的正合序列P=…→P1→P0→P0→P1→…使得M≅Im(P0→P0), 且对任意投射R-模Q, HomR(-,Q) 仍保持 序列P的正合性. 对偶地, 可定义Gorenstein内射模. 作为对Gorenstein投射与内射模的推广, 2015 年, Pan等[7]对两个给定的R-模类X与Y, 介绍并研究了 (X,Y)-Gorenstein 投射与内射模类, 考察了各种 (X,Y)-Gorenstein 投射模之间的关系. 笔者继续研究 (X,Y)-Gorenstein 投射与内射模的一些同调性质, 并给出模的 (X,Y)-Gorenstein 投射与内射维数的等价刻画, 推广了已有Gorenstein 投射与内射模的相关结论.

本文中环R均指有单位元的结合环, 模均指左R-酉模. 用P表示投射R-模类,I表示内射R-模类,FI表示FP-内射R-模类,GI表示Gorenstein内射R-模类,N表示正整数集.

1 (X,Y)-Gorenstein 投射与内射模的同调性质

定义1.1[4]X,Y是两个R-模类,M是R-模.

1) 称正合序列

X=…→X1→X0→M→0

为M的左X-分解, 如果对所有i≥0,Xi∈X.

2) 称正合序列

Y=0→M→Y0→Y1→…

为M的右Y-分解, 如果对所有i≥0,Yi∈Y.

3) 称序列Y是HomR(X,-)(HomR(-,X)) 正合的, 如果对任意X∈X, 序列HomR(X,Y)(HomR(Y,X)) 正合.

定义1.2[7]设X,Y是两个R-模类且P⊆X. 称R-模M是(X,Y)-Gorenstein投射模, 如果存在正合序列

X=…→X1→X0→X0→X1→…

使得:

1) 对所有i0,Xi,Xi∈X;

2)M≅Im(X0→X0);

3) 序列X是HomR(-,Y) 正合的.

设X,Y是两个R-模类且I⊆Y. 称R-模M是 (X,Y)-Gorenstein内射模, 如果存在正合序列

Y=…→Y1→Y0→Y0→Y1→…

使得:

1) 对所有i0,Yi,Yi∈Y;

2)M≅Im(Y0→Y0);

3) 序列Y是HomR(X,-) 正合的.

记 (X,Y)-Gorenstein投射与内射R-模类分别为 (X,Y)-G P与 (X,Y)-G I.

由文献 [7] 可知对偶于关于 (X,Y)-Gorenstein 内射模的每一个结论都可得 (X,Y)-Gorenstein 投射模的相应结论. 因此, 以下我们只讨论关于 (X,Y)-Gorenstein 内射的情形.

注记1.1 1) 根据定义可知Y⊆(X,Y)-G I.

2) 序列Y中每个态射的核, 余核, 象都是 (X,Y)-Gorenstein 内射模.

3) 若X=I, Y=I, 则(X,Y)-Gorenstein 内射模即通常的 Gorenstein 内射模[2].若X=FI, Y=I,则 (X,Y)-Gorenstein 内射模即 GorensteinFP-内射模[6]或Ding内射模[3]. 若X=G I, Y=I,则 (X,Y)-Gorenstein内射模为内射模[8]. 若I⊆X, Y=I,则 (X,Y)-Gorenstein 内射模为X-Gorenstein 内射模[8].

定义1.3 设X是一个R-模类,M是R-模. 定义M的X内射维数

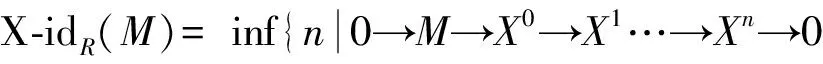
若这样的n不存在, 则规定X-idR(M)=∞.

特别地, 当X=(X,Y)-GI时, 用 (X,Y)-GidR(M)表示M的 (X,Y)-GI内射维数.

命题1.1 设M是R-模. 则以下条件等价:

1)M∈(X,Y)-GI.

3) 存在短正合序列 0→K→Y→M→0使得Y∈Y,K∈(X,Y)-GI.

命题1.1的证明 1)⟺2)⟹3)由 (X,Y)-Gorenstein 内射模的定义得.

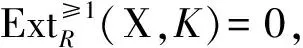
…→Y1→Y0→K→0.

因此M存在HomR(X,-) 正合的左Y-分解

…→Y1→Y0→Y→M→0.

用HomR(X,-) 作用于短正合序列 0→K→Y→M→0, 可得长正合序列

根据命题 1.1 与维数转移可得以下结论.

推论1.1 设R-模M是(X,Y)-Gorenstein 内射模. 则对任意具有有限X内射维数的R-模L, 有

命题1.2 设0→M′→M→M″→0 是R-模的短正合序列. 则以下结论成立:

1) 若M′,M″∈(X,Y)-GI, 则M∈(X,Y)-GI.

2) 若M′,M∈(X,Y)-GI, 则M″∈(X,Y)-GI.

3) 若R-模类Y关于直积封闭, 则 (X,Y)-GI关于直积与直和项封闭.

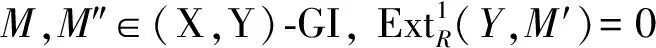
2) 因为M∈(X,Y)-GI, 所以存在R-模的 短正合序列0→K→Y→M→0 使得Y∈Y,K∈(X,Y)-GI. 考虑以下拉回图:

因为K,M′∈(X,Y)-GI, 所以由1)知T∈(X,Y)-GI. 再由命题 1.1 3)可得M″∈(X,Y)-GI.

3) 因为Y关于直积封闭, 所以 (X,Y)-GI也关于直积封闭. 再由1), 2)及文献[4]中命题 1.4 可得(X,Y)-GI 关于直和项封闭.

4) 因为M″∈(X,Y)-GI, 所以存在R-模的短正合序列 0→K→Y→M″→0 使得Y∈Y,K∈(X,Y)-GI. 考虑拉回图:

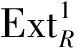
2 (X,Y)-Gorenstein 投射与内射维数

根据命题1.1与维数转移可得以下结论.

命题2.1 设

再次，大学生基础水平以及学习方法因素。大学学习阶段，学生的学习具有很强的自主性、目的性以及选择性，其学习目的多数是为了未来的发展或兴趣。部分学生没有正确认识大学学习的特点，从而一直采取高中所用的学习方法，在课堂接受知识与课后巩固知识、拓展知识等方面存在很大的困难，部分学生还存在严重的偏科现象，在理解知识方面的困难增大。还有部分学生的学习能力较差，其阅读、分析、理解、推理以及应用知识的能力较差，也使得其出现学业问题。[2]

0→M→G0→…→Gn-1→Kn→0

是R-模的正合序列. 若每个Gi∈(X,Y)-GI, 则对任意具有有限X内射维数的R-模L及任意i∈, 有≅).

定理2.1 设M是R-模且 (X,Y)-GidR(M)=n<∞. 则存在正合序列

0→M→G→Y→0,

0→G′→Y′→M→0

使得G′,G∈(X,Y)-G I, Y-idR(Y′)≤n, Y-idR(Y)≤n-1(当n=0 时,Y=0).

定理2.1的证明 对n进行归纳. 当n=0 时,M∈(X,Y)-GI.由命题 1.1 3) 知存在正合序列 0→M→M→0→0和0→G′→Y′→M→0 使得Y′∈Y,G′∈(X,Y)-GI.若 (X,Y)-GidR(M)=n>0, 则存在正合序列

0→M→G0→G1→…→Gn→0

使得每个Gi∈(X,Y)-GI. 令K1=Im(G0→G1). 则有正合序列

0→M→G0→K1→0,

0→K1→G1→…→Gn→0.

因此 (X,Y)-GidR(K1)≤n-1. 由归纳假设知存在正合序列 0→G″→Y″→K1→0 使得Y-idR(Y″)≤n-1,G″∈(X,Y)-GI. 考虑拉回图:

由命题 1.2 1) 知G∈(X,Y)-GI, 于是存在正合序列 0→G′→L→G→0 使得L∈Y,G′∈(X,Y)-GI.考虑拉回图:

由上图中中间一行的正合性可知Y-idR(Y′)≤n. 因此 0→M→G→Y″→0和0→G′→Y′→M→0 即为所需正合序列.

根据推论 1.1 与定理 2.1 可得以下结论.

推论2.1 设M是R-模且(X,Y)-GidR(M)=n<∞. 若Y⊆X, 则M存在长度为n的HomR(-,(X,Y)-GI)正合的右(X,Y)-GI-分解.

命题2.2 设 0→M→G0→G1→K→0 是R-模的正合序列. 若G0,G1∈(X,Y)-GI, 则存在以下正合序列

0→M→G→Y→K→0, 0→M→Y′→G′→K→0

使得Y,Y′∈Y,G,G′∈(X,Y)-GI.

命题2.2的证明 因为G1∈(X,Y)-GI, 所以存在短正合序列0→G2→Y→G1→0 使得Y∈Y,G2∈(X,Y)-GI. 令L=Im(G0→G1). 考虑拉回图:

和拉回图：

因为G0,G2∈(X,Y)-GI, 所以由命题 1.2 1) 可知G∈(X,Y)-GI. 因此由短正合序列 0→M→G→C→0 与0→C→Y→K→0 即得所需正合序列 0→M→G→Y→K→0, 其中Y∈Y,G∈(X,Y)-GI.

同理, 存在正合序列 0→M→Y′→G′→K→0 使得Y′∈Y,G′∈(X,Y)-GI.

命题2.3 设 (Mi)i∈I是一簇R-模,I是指标集. 若R-模类Y关于直积封闭, 则

(X,Y)-GidR(∏Mi)=sup{(X,Y)-GidR(Mi)|i∈I}.

命题2.3证明 因为 (X,Y)-GP关于直积封闭, 所以“≤”显然成立. 因此只需证明“≥”成立即可, 即需证明若M′是M的直和项, 则(X,Y)-GidR(M′)(X,Y)-GidR(M).

设(X,Y)-GidR(M)=n<∞.对n进行归纳. 当n=0时,M∈(X,Y)-GI. 由命题1.2的3)知M′∈(X,Y)-GI, 所以 (X,Y)-GidR(M′)=(X,Y)-GidR(M)=0. 若n>0,记M=M′⊕M″. 取正合序列0→M′→I′→K′→0 和0→M″→I″→K″→0, 其中I′,I″∈I. 考虑交换图:

0 0 0

0 0 0由上图中中间一列的正合性可知 (X,Y)-GidR(K′⊕K″)=n-1. 因此由归纳假设得 (X,Y)-GidR(K′)≤(X,Y)-GidR(K′⊕K″)=n-1, 所以(X,Y)-GidR(M′)≤n, 即 (X,Y)-GidR(M′)≤(X,Y)-GidR(M).

以下定理推广了文献 [4] 中定理 2.22 及文献 [8] 中命题 2.15.

定理2.2 设M是R-模且(X,Y)-GidR(M)<∞,n是自然数. 则以下条件等价:

1) (X,Y)-GidR(M)≤n.

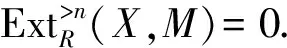
4) 对每个R-模的正合序列

0→M→G0→…→Gn-1→Kn→0.

若Gi∈(X,Y)-GI,Y⊆X且Y关于直积封闭, 则Kn∈(X,Y)-GI.

5) 对任意0≤t≤n的整数t, 存在R-模的正合序列

0→M→C0→…→Ct→…→Cn→0

使得Ct∈(X,Y)-GI,Ci∈Y(i≠t).

6) 对任意0≤t≤n的整数t, 存在R-模的正合序列

0→M→C0→…→Ct→…→Cn→0

使得Ct∈Y,Ci∈(X,Y)-GI(i≠t).

7) 对任意1≤t≤n的整数t, 存在R-模的正合序列

0→M→C0→…→Ct→…→Cn→0

使得Ci∈(X,Y)-GI(0≤i

8) 对任意1≤t≤n的整数t, 存在R-模的正合序列

0→M→C0→…→Ct→…→Cn→0

使得Ci∈Y(0≤i

定理2.2的证明 1) ⟹ 2) 因为 (X,Y)-GidR(M)≤n, 所以存在正合序列

0→M→G0→…→Gn-1→Gn→0

2)⟹3)显然.

3)⟹4)考虑正合序列

0→Kn→H0→…→Hm-1→Hm→0

4)⟹1) 显然.

5)⟹1) 显然.

1)⟹5) 对n进行归纳. 当n=0时, 结论显然成立. 假设n≥1.因为(X,Y)-GidR(M)≤n, 所以存在正合序列

0→M→G0→G1→…→Gn→0

使得每个Gi∈(X,Y)-GI. 令K1=Im(G0→G1). 则(X,Y)-GidR(K1)≤n-1. 由归纳假设知存在正合序列

0→K1→C1→…→Ct→…→Cn→0

使得Ct∈(X,Y)-GI(1≤t≤n),Ci∈Y(i≠t). 因此只需证明当t=0 时结论成立即可.考虑正合序列

0→K1→C1→C2→…→Cn→0,

其中C1∈(X,Y)-GI,Ci∈Y(i≠1).令K2=Im(C1→C2). 则有短正合序列0→K1→C1→K2→0, 因此有正合序列0→M→G0→C1→K2→0, 其中G0,C1∈(X,Y)-GI. 再由命题 2.2可知存在正合序列0→M→C0→Y→K2→0 使得Y∈Y,C0∈(X,Y)-GI. 因此存在正合序列

0→M→C0→…→Ct…→Cn→0

使得C0∈(X,Y)-GI,Ci∈Y(i≠0).

类似于1) ⟺5) 的证明方法可得1)⟺6),1)⟺7),1)⟺8).

推论2.2 设M是R-模且(X,Y)-GidR(M)<∞. 则有

[1] Auslander M, Bridger M. Stable module theory[M]. Providence, RI:Mem Amer Math Soc 94,1969.

[2] Enochs E E, Jenda O M G. Gorenstein injective and projective modules[J]. Math Z, 1995, 220: 611-633.

[3] Gillespie J. Model structures on modules over Ding-Chen rings[J]. Homology Homotopy Appl, 2010, 12: 61-73.

[4] Holm H. Gorenstein homological dimensions[J]. J Pure Appl Algebra, 2004, 189: 167-193.

[5] Huang C H, Huang Z Y. Gorenstein syzygy modules[J]. J Algebra, 2010, 324: 3408-3419.

[6] Mao L X, Ding N Q. Gorenstein FP-injective and Gorenstein flat modules[J]. J Algebra Appl, 2008(7): 491-506.

[7] Pan Q X, Cai F Q. (X,Y)-Gorenstein projective and injective modules[J]. Turkish J Math, 2015, 39: 81-90.

[8] Meng F Y, Pan Q X. X-Gorenstein projective and Y-Gorenstein injective modules[J]. Hacettepe Math, 2011, 40: 537-554.

[9] Enochs E E, Jenda O M G. Relative homological algebra[M]. Berlin, New York:Walter de Gruyter, 2000.

(责任编辑 赵燕)

(X,Y)-Gorenstein homological dimensions

SONG Jie, ZHANG Chunxia

(College of Mathematics and Statistics, Northwest Normal University, Lanzhou 730070, China)

We investigate some basic homological properties of (X,Y)-Gorenstein projective and injective modules and introduce some equivalent characterizations of (X,Y)-Gorenstein projective and injective dimensions of modules.

homologic properties;(X,Y)-Gorenstein projective(injective)module; (X,Y)-Gorenstein projective(injective)dimension

2016-03-27

国家自然科学基金(11401475)资助

宋洁(1991-)，女，硕士生，E-mail:songjie2728@153.com;zhangcx@nwnu.edu.cn

1000-2375(2017)01-0076-06

O153.3

A

10.3969/j.issn.1000-2375.2017.01.015