在初中数学教学中渗透数形结合思维

【摘 要】在新课程的要求下,各个学科教师都积极的对课程进行了改革,在改革的过程中学生和教师都会出现“水土不服”的现象,所以教师一定要合理、有针对性的对新教学方式进行渗透。初中数学作为初中比较重要而且知识点比较难的学科,更应该选择合理的教学方式。由于初中数学涉及到很多数字的运算和繁杂的理论知识,所以将这些繁琐的知识通过图形表现出来会更加的直观,经教师集体讨论和研究一致认为数形结合思想更适合初中数学教学。
【关键词】数形结合思想;初中数学;渗透
初中数学是一门比较难理解的学科,在新课程的要求下我国的传统教育亟待改革,所以在教师们的积极探索下新的教学思想被提出。数形结合思想是将繁琐的理论通过图形展现出来,使学生能够更直观的看到知识框架,使复杂的文字描述简单化,学生更容易理解教学内容,有助于学生理清知识脉络。
一、数形结合的意义
数形结合是指将理论描述与图形有机的结合在一起,学生可以通过图形理清知识脉络,并且通过文字描述进一步了解理论知识。使学生在学习过程中思路更加清晰,通过这样的方法吸引学生的注意力。同时,数形结合思想不再是枯燥的文字和数字,在学习的过程中加上形象的图形可以激发学生的学习兴趣,并且通过数形结合思想的熏陶,可以提高学生的思维能力,总结能力,分析能力,空间构图能力等综合能力,数形结合思想可以将复杂的问题简单化,复杂的文字和数字直观化,繁琐的计算明了化,所以数形结合非常符合初中数学教学。
二、数形结合的基本应用方法
数形结合思想在初中数学应用上是有效的,但是在应用中仍需要注意一些基本操作方法,数学结合思想不能直接硬套在初中数学教学中,而是要通过逐步的渗透,使学生逐渐接受,最后熟练运用。
(一)在数学概念上初步渗透
数学概念多数比较抽象,学生在阅读文字描述的概念时不容易理解,对概念理解模糊会影响学生知识的掌握和应用,所以数形结合思想需要在数学概念上初步渗透,通过图形的直接表述,能够使学生更容易理解。比如,对称轴:如果一个图形沿某条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形;这条直线叫做对称轴。初中生的理解能力是有限的,所以学生在读这段文字时很难准确的理解对称轴的概念,那么教师就可以通过画图的方式让学生直观的看到对称轴的意义。(如图2所示)MN即为对称轴,通过画图直接的将对称轴展现给学生,学生能够通过看图形迅速的领略对称轴的意义。
(二)对典型例题的渗透
典型的例题对学生知识点的掌握起主要作用,所以接下来教师要适当的将数形结合思想渗透到典型例题中,通过画图解题,学生能够更清楚的理解题意,并且避免繁琐的计算过程,所以画图解题法更适合。比如,不等式组x+4>3
x≤1
求解。学生在解这道题的时候会涉及到计算,而且结果不容易验证但通过画图就可以直观的看到答案,并且不容易出现错误
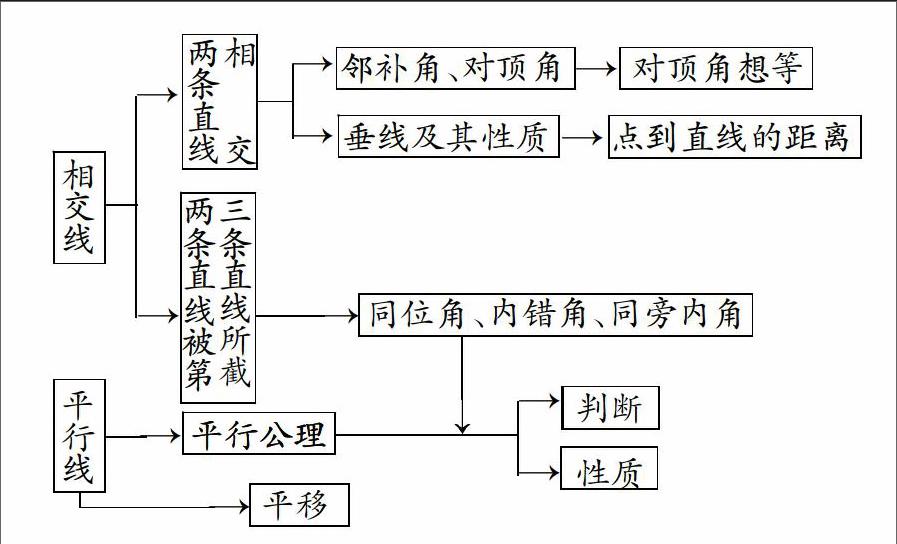
通过这个图形学生很清晰的看到答案, 再将图形翻译成文字-1 (三)整个知识框架的渗透 教学活动中,书本的知识是有限的,所以教师在教学过程中不能仅仅是对课本知识的传授,还要教给学生学习方法和思维方式,“授人以鱼不如授人以渔”。所以,在学生了解了数形结合思想后,教师要适当的放手让学生利用数形结合法去总结整个章节或者知识点的框架。首先学生要通过对知识的复习进行文字整理,然后将文字翻译成图形,通过直观的图形形成知识网络储存在学生的头脑中,在需要应用的时候再转化成文字。比如:相交线与平行线(人教版七年级上册)这一章的内容,通过语言总结为:相交线、邻补角、对顶角、垂线、同位角、内错角、同旁内角、平行线、平移等定理和性质。然后对比较重要的性质进行特殊标记,如平行公理、垂线性质等。这种语言总结看起来不直观,而且整个知识点过于分散,不方便学生的学习和记忆。面对复杂的文字叙述和难以理解的语句意思,学生容易产生厌烦心理,不利于学生的学习。 而通过图形构建框架为: 图形的框架看起来更直观,有助于学生对知识点的复习,而且不容易遗漏知识点,每个知识点间都可以找到相应的联系,简单明了的知识网络使学生对学习更感兴趣。 三、结语 综上所述,数形结合思想在初中数学教学中已经初见成效,数形结合通过数字与图形的转换,使抽象的数学问题更具体化,学生可以通过图形更直观的理解定义,分析习题,总结知识框架。数形结合教学思想提高了学生的创新能力、空间构造能力、分析能力等综合能力。在很大程度上提高了学生的学习兴趣和自主学习能力,从而达到预期的学习效果。 【参考文献】 [1]陈晔.数学教学中数形结合思想的渗透[J].语数外学习(数学教育),2013(11):134 [2]张丽.数形结合思想在初中数学教学中的应用[J].中学生数理化(教与学),2015(5):67-67 [3]龙云.数形结合思想在初中数学教学中的实施[J].新课程·中学,2014(7):213-213

