2016年全国高考试卷中“数列”试题分析
☉西北师范大学教育学院 张定强 闫佳洁
2016年全国高考试卷中“数列”试题分析
☉西北师范大学教育学院 张定强 闫佳洁
数列既是高中数学体系中的重要内容,也是学习高等数学的重要基础.作为一种特殊的函数,是反映自然界变化规律的基本数学模型,常与其他数学知识紧密联系.命题者依据《普通高中数学课程标准(实验)》(以下简称《课标》)的要求,把数列作为考点进行命题,以考查学生基础知识、数学思想、数学联系的掌握程度,本文对2016年全国高考数学试卷中数列试题的特点进行分析,并提出了一些教学建议.
一、各地区试卷对“数列”知识考查的题型及分值分析
2016年高考数学文、理科共19套试卷,都对数列知识进行了考查,其中7个地区自主命题(北京、天津、上海、江苏、浙江、山东、四川文理各一套,江苏省文理为同一套)有13套试卷,其余各地区分别使用新课标卷I(河北、江西、安徽、福建、河南、广东、湖南、湖北、山西、广西)、新课标卷Ⅱ(甘肃、吉林、宁夏、重庆、青海、西藏、黑龙江、辽宁、新疆、内蒙古、海南、山西、贵州、云南)、新课标卷Ⅲ(广西)共6套试卷.2016年全国19套高考数学试卷按照题型和分值统计结果如表1:
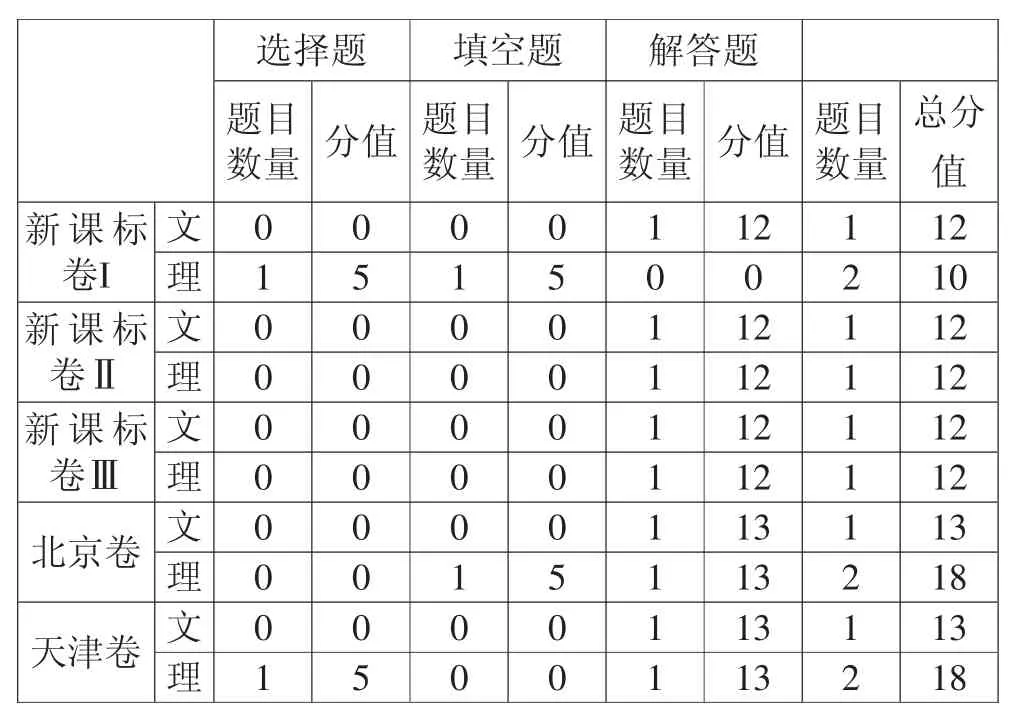
表1 2016年高考数学各套试卷对数列考查题型及分值统计表
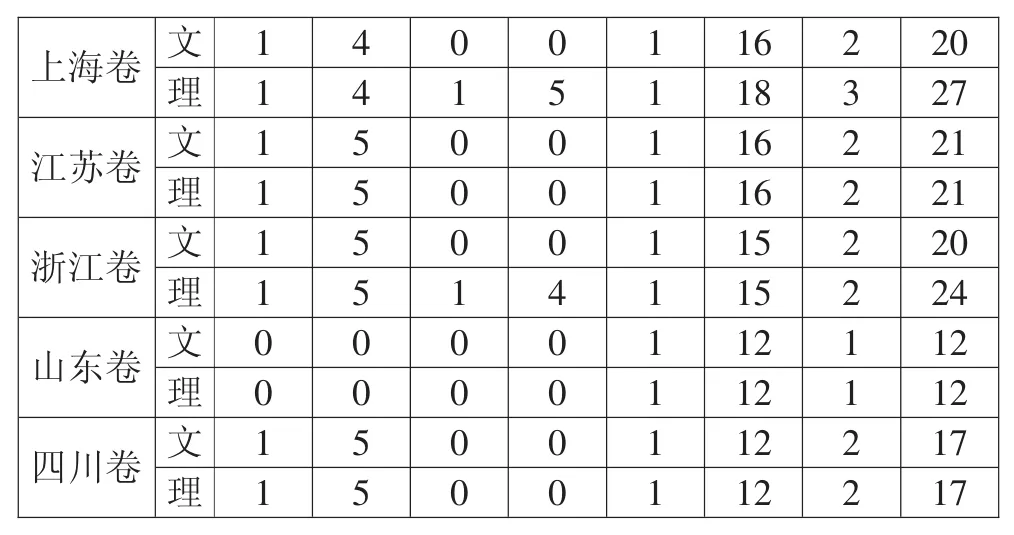
上海卷文 1 4 0 0 1 16 2 20理1 4 1 5 1 18 3 27江苏卷文 1 5 0 0 1 16 2 21理1 5 0 0 1 16 2 21浙江卷文 1 5 0 0 1 15 2 20理1 5 1 4 1 15 2 24山东卷文 0 0 0 0 1 12 1 12理0 0 0 0 1 12 1 12四川卷文 1 5 0 0 1 12 2 17理1 5 0 0 1 12 2 17
从统计数据来看,2016年高考数学对数列知识的考查题目个数是9套试卷1题、10套试卷2道,1套试卷3题,差异不大.从题型的角度看,选择题仅在10套试卷中出现了数列题,分值是4或5分;填空题仅在4套试卷中出现了数列题,分值也是4或5分;除新课标卷I理科卷外,解答题在其他试卷中都有一道数列题出现,分值分布在区间[12,18]内,大多是12~13分.总之,数列方面的试题在选择题与填空题方面出现题量差异较大,而在解答题的题量方面相对稳定.
从新课标卷和自主命题试卷来看,除新课标Ⅰ理科卷外,数列在所有的新课标卷的选择题和填空题方面都没出题;而自主命题试卷只有北京文、天津文和山东卷在数列方面没有出填空题、选择题.由此知道,2016年高考数学19套试卷均考查了数列知识,相比自主命题卷,新课标卷对数列知识的考查题量较少,或者只在大题(解答题)中考查,或者只在小题中考查,而自主命题试卷则对数列知识考查题量较多,大部分自主命题地区大题小题都有.
从文理科卷来看,文科卷共有14道题,总分是152,占每套试卷分值的10.13%;理科卷共有18道题,总分170,占每套试卷分值的11.33%.足见数列知识是高考数学考查的重点内容之一.
二、各地区试卷对“数列”知识考查的试题特点分析
分析2016年高考数学试卷中的数列试题,发现有如下4个方面的特点.
1.以考查等差、等比数列知识为主
《课标》中明确写道:“通过实例,理解等差数列、等比数列的概念”,“探索并掌握等差数列、等比数列的通项公式与前n项和的公式”,[1]而今年的数列考题命题者正是按照《课标》的要求重点考查了等差、等比数列的相关知识;19套高考数学试卷中均有等差数列或等比数列的题目,大部分数列的题目是以解答题形式考查了等差数列或等比数列的相关知识,如通项公式、性质、前n项和等.
例1(北京卷理12)已知{an}为等差数列,Sn为其前n项和,若a1=6,a3+a5=0,则S6=_______.
分析:此题给出了等差数列{an}的首项,并且所给出的项都是奇数项,通过等差数列的性质可得到a4=0,从而得到公差d=-2,进而通过首项和公差很容易就会求得前6项之和为6.
例2(新课标卷Ⅰ文17)已知{an}是公差为3的等差数列,数列{bn}满足
(Ⅰ)求{an}的通项公式;
(Ⅱ)求{bn}的前n项和.
分析:题目给出了{an}是等差数列,对数列{bn}只给出了第一项和第二项.对第一问,从已知的等式中,不难观察出当n=1时,等式变为a1b2+b2=b1,容易得到{an}的首项,进而得到通项公式an=3n-1;联系第一问中求得的{an}的通项公式,代入等式,化简可找到bn与bn+1之间的关系,得到{bn}是等比数列,进而可以求得前n项和Sn=
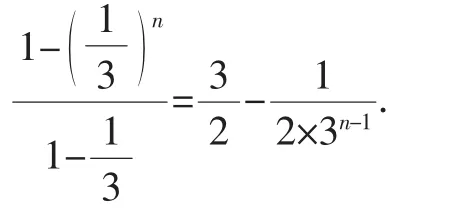
2.关注知识间的交叉融合性
分析高考数学试卷中数列知识的考点,发现通常是与相关的知识点联合考查.数列本身与相关的知识进行融合就会命制出更多精彩的数列试题来.[2][3]试题的交叉融合性越大,对学生的要求就越高,既需要学生清晰地掌握数列知识,又需要学生掌握与之相关知识间的联系,把数学知识真正学“透”、学“通”,才能迎接数学思维能力和解题方法的挑战.就今年试题而言,发现数列与不等式、集合、极限、充要条件、二次函数性质、对数函数性质、三角函数性质、双曲线性质,以及几何中三角形的边和面积知识点等相融合的综合试题较多.
例3(上海卷理17)已知无穷等比数列{an}的公比为q,前n项和为Sn,且下列条件中,使得2Sn A.a1>0,0.6 C.a1>0,0.7 分析:这道题目给出的是一个无穷等比数列,与极限知识综合考查,要求根据给出的条件判断a1和q的范围.从已知条件和2Sn 例4(天津卷文18)已知{an}是等比数列,前n项和为Sn(n∈N*),且 (Ⅰ)求{an}的通项公式; (Ⅱ)若对任意的n∈N*,bn是log2an和log2an+1的等差中项,求数列{(-1)nb2}的前2n项和. n 分析:本题看似是常规题,重点考查等差、等比数列及数列求和,但在第二问中将对数运算与数列知识巧妙地结合在一起,得到数列{bn}的通项公式过渡自然,内涵丰富. 3.试题中植入创新因子,体现创新意识 《课标》中的具体目标之一就是“发展学生的应用意识和创新意识”.[1]纵观2016年的所有数列考题,就会发现,对于一些数列知识的考查,命题者会利用一些数学知识进行内涵挖掘和外延拓展,如自定义数列,命制一些符合某些特殊条件的数列让考生进行研究,既能考查数列的某些性质与判定,又能够与其他部分的知识联动考查,真正考查学生的创新能力.[4] 例5(新课标卷Ⅱ文17)等差数列{an}中,a3+a4=4,a5+a7=6. (Ⅰ)求{an}的通项公式; (Ⅱ)设bn=[an],求数列{bn}的前10项和,其中[x]表示不超过x的最大整数,如[0.9]=0,[2.6]=2. 分析:本题第一问是常规题,考查通性通法;第二问数列{bn}是自定义数列,解决这一创新问题,就要从新的定义中找到数列{bn}的本质,如果学生对{bn}的定义出现的取整理解偏差,把握不准确,在解决问题的过程中就会出现错误,如果正确理解,就能顺利解决这个问题,得{bn}的前10项和为1×3+2×2+3×3+4×2=24. 例6(上海卷文22)对于无穷数列{an}与{bn},记A={x|x=a,n∈N*},B={x|x=bn,n∈N*},若同时满足条件:①{an},{bn}均单调递增;②A∩B=ø且A∪B=N*,则称{an}与{bn}是无穷互补数列. (1)若an=2n-1,bn=4n-2,判断{an}与{bn}是否为无穷互补数列,并说明理由; (2)若an=2n且{an}与{bn}是无穷互补数列,求数列{bn}的前16项的和; (3)若{an}与{bn}是无穷互补数列,{an}为等差数列且a16=36,求{an}与{bn}的通项公式. 分析:本题给出了无穷互补数列的定义,第一问要判断两个数列是否为无穷等比数列,学生要么能够找到一组反例不满足无穷等比数列其中的任何一个条件,得出结果,要么能够证明两组数列是无穷等比数列,而这道题刚好是前者,所以降低了难度;第二问通过已知条件推导,自然地过渡到了数列求和的分组求和上,让学生体会数学变换的奇特之美;第三问看似是常规的求数列通项公式的题目,实际上还考查到了分类讨论的数学思想,内涵丰富. 4.不同试卷数列试题难易程度有差异性 2016年的高考数学试卷中对于数列的考查,从运算的复杂程度和知识的综合性与交叉性来看,文科和理科难易程度有所不同,新课标卷与自主命题试卷难易程度也有所不同,大致呈现出文科较理科简单,新课标卷较自主命题试卷简单的态势. (1)同一地区文、理科试题难度适当有别. 今年的高考数学试卷只有江苏卷出现了文理合卷的情况,其他地区是文、理科分考.文、理科试题对于数列的考查在题目个数、题型及试题难度上均有所差异;部分地区为了使文理科差异保持适度,命题的数量和题型保持一致,但理科卷比文科卷在运算和知识交叉上较复杂,如山东卷.也有部分地区的高考题中,对数列的考查,理科卷从题目个数、题型、试题难度上均比文科卷要复杂,如北京卷.运用曹一鸣与吴立宝例习题难度的计算方法计算,[5]发现同一地区文、理科试题难度适当有别,如山东卷文科的难度值为1.56,理科的难度值为1.75;北京卷文科的难度值为1.94,理科的难度值为2.31,从数据可以看出山东卷和北京卷的理科卷难度值均大于文科卷难度值. (2)不同地区试题难度不同. 从所有高考试卷中数列题目来看,大部分自主命题试卷对数列的要求高于新课标卷的要求,尤其是在运算的复杂程度、知识的交叉性与综合性、创新性上较为突出,如北京、天津、上海、江苏、四川和浙江.用同样的计算方法可知,不同地区试题难度不同,如新课标卷Ⅱ理科难度值为2.215,北京卷理科难度值为2.31,四川卷理科难度值为2.327,显然,北京卷理科和四川卷理科的难度值要大于新课标卷Ⅱ理科的难度值. 根据以上分析,不难发现,高考试题对数列的考查集中在对等差、等比数列的考查,大部分试题与其他方面的知识相结合,对学生创新意识与能力的考查不断加强,在教学中: 1.紧扣考纲,打好基础 2016年高考数学试题中的数列部分,紧扣考纲考查基本概念,重点考查等差、等比数列相关概念的性质、求公差和公比、通项公式、前n项和等方面的知识,虽然试题千变万化,但都以基础知识、基本能力、基本思想、基本活动经验为基础.所以在教学中,要以课标为基础,围绕教科书,紧扣考纲,对重点内容,如上述所提的知识点要重点复习,夯实基础知识,训练学生灵活思维方式,特别是与其他知识相融合后处理问题的方式方法,以提高学生应对高难度试题的能力. 2.注重数列与其他知识的综合性复习 综合分析近几年高考数学试卷中关于数列的试题,大部分试题都是与其他数学知识相关联而命题的,体现了知识之间的融合性,所以在教学中,要创设多种途径,如用画思维导图、专题讲座等形式不断沟通数列与三角函数、二次函数、指对幂函数、三角形边角关系、不等式、极限等知识之间的联系,通过例题、习题、检测等方式来强化数学知识之间的相互联系,让学生在解决问题的过程中灵活运用数列相关的数学思想方法及解决问题模型,体会这些思想方法在解决综合问题中的力量. 3.精细化创设问题情景以提高学生的创新意识 分析这几年的高考试题,创新意识在高考试题中逐步彰显,也成为命制数列试题的一大亮点;这就要求在日常的数学教学中,要不断创设问题情景,围绕问题型、方法型、命题型情境创设,重点基于生活情境、科学情境、文化情境、思维情境形成数列方面的情景场域,使学生的学习高效,便于理解、诠释、反思、探究、创造的深入,更好地理解数列方面的核心概念、掌握数学思想方法,盘活资源,激活思维,提高学生的创新思维,使学生能够较好地应对一些创新试题,从而提高学生数学思维品质,形成创新意识. 1.中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京:人民教育出版社,2003. 2.刘会金.2014年高考“数列”专题分析[J].中国数学教育(高中版),2014(7-8). 3.刘会金.2012年高考“数列”专题分析[J].中国数学教育(高中版),2012(7-8). 4.高慧明,高宇.全国高考数学“压轴题”分类研析——以“数列”为主体[J].中学数学研究,2013(3). 5.曹一鸣,吴立宝.初中数学教材难易程度的国际比较研究[J].数学教育学报,2015(4).三、高中数学“数列”教学的三点建议

