迭代算法的平方收敛

汤 涛

（南方科技大学数学系 518055）

给定一个函数f（x）以及一个初始值x0，然后重复地计算

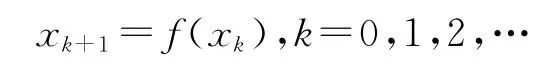
就叫迭代法.

迭代法在人类有了计算机以后产生了巨大的作用.它利用计算机运算速度快、适合做重复性操作的特点、让计算机重复执行一组指令（或一定步骤）、在每次执行这组指令（或这些步骤）时、都从变量的原值推出它的一个新值.虽然迭代法的思想产生在很久以前，包括阿基米德、刘徽都用过，但在计算机出现以前，迭代法仅仅具有算法思想，难以付诸实用，其生命力也就非常有限了.

1 迭代算法求根

一个最典型的迭代法的例子就是开根号.假设我们不知道如何开根号，这样就没有办法求.

换一个思路.我们问如何求x2-2=0的根或其近似根？考虑x2-2=0的一个等价形式：

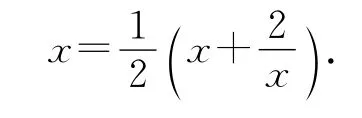
这就可形成一个迭代算法：大概地给定一个初始近似值x0，通过下面的公式逐次形成x1，x2，…：

即不断令xk+1等于xk和2/xk的算术平均数，迭代六、七次后得到的值就己经相当精确了.

例如，假设首先猜测根号2的初始近似值为1，虽然它不是很准确，但从表1可以看到：使用迭代法（1）后，迭代值很快趋近于.注意到迭代6次有近50位有效数字，而迭代7次就有近100位的有效数字！

为什么会有这么好的精确度呢？

下面我们做一些简单分析.由（1），根据算术平均数大于几何平均数得出：

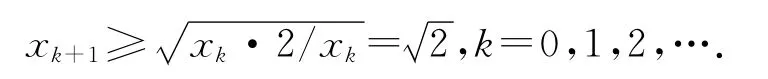
表1 迭代算法（1）前7次迭代后的近似值；底下划线部分是精确值

另一方面，仍由（1）可以得到：

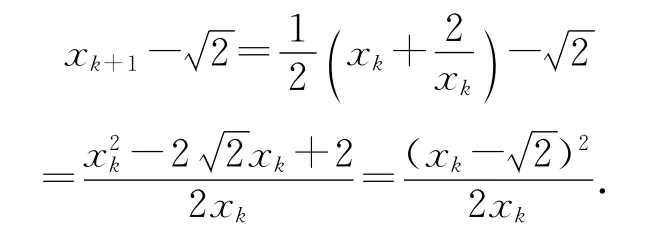
结合上面这两个结果可以得到：

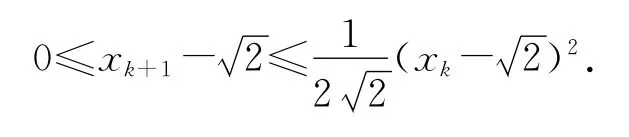
这种性质称为二次收敛或平方收敛.具有这种性质的算法收敛非常快，每迭代一步就可以加倍小数点后面的有效数字.比如一开始的误差是10-1，在迭代6次的过程中产生的误差分别是10-2，10-4，10-8，10-16，10-32，10-64的量级！

那么，是不是每个迭代公式部可以收敛得这么快呢？笞案是否定的.比如考虑求的近似值、通过下面这个恒等式：

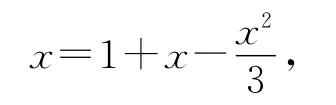
可以得到迭代公式

这个迭代对任何给定的初始值x0都是收敛的.如取初始值为x0=3就可以得到表2的结果.这时，区别就看出来了：对于迭代算法（2）、迭代7次以后，仅能得到5位有效数字，而不是前面例子断给出的近100位有效数字.

表2 迭代算法（2）前7次迭代后的近似值

笞案是肯定的.我们还是考虑下面的形式：

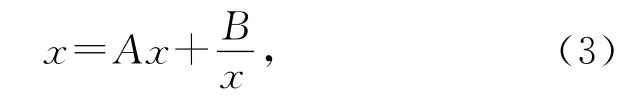
其中A，B为待定系数.首先需要（3）和x2=3等价，也就是说：

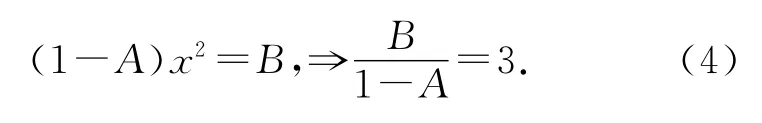
另一方面，对于迭代公式xk+1=A xk+B/xk可以推出

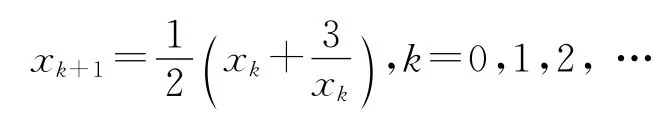
满足

2 求圆周率的平方收敛算法

目前最快的计算圆周率的迭代算法基于高斯（Karl Gauss，1777—1855）和勒让德（Adrien-Marie Legendre，1752—1833）的纯数学理论，它于19 75年被布伦特（Richard Brent）和萨拉明（Eugene Salamin）提炼为适合计算机计算的现代算法.此算法以迅速收敛著称，只需25次迭代即可产生π的45 00万位正确数字.日本筑波大学于2009年8月17日宣布利用此算法计算出π小数点后2500多亿（2，576，980，370，000）位数字.

下面给出高斯-勒让德算法：选取初值

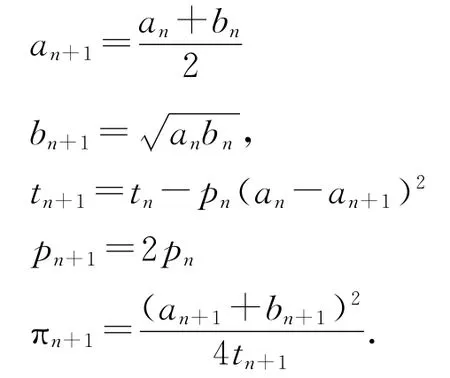
此算法之所以被称为高斯一勒让德算法，是因为这两位大数学家贡献了原始思想；在19世纪，高斯己经知道算术一几何平均迭代可以导致二次收敛，就象上节通过近似求解的例子那样具有快速的收敛性质；而勒让德推导出的一个关于椭圆积分的恒等式是算法成功的一个重要保证.

在上表的算例中，我们先取n=0，算出a1，b1，t1，p1，π1的值，之后再让n=1，重复下去，就会得到一系列的数据πn来近似π.从数值结果可以看出，高斯-勒让德算法是平方收敛的，即如上节例子所演示的那样，误差随着迭代次数成平方阶递减.特别地，迭代3次后就可以得到19位有效数字，迭代5次就可以得到84位，迭代6次后有效数字171，而迭代7次时，有效数字就增加为345.

由于篇幅限带，高斯-勒让德算法的平方收敛推导将不在此给出.有兴趣的读者可以参考作者近期准备的一个小册子[1].