自平衡试桩法桩基承载力等效转换新方法

谭现江，杨高尚，雷明锋,2，陈树林，李玉峰，2

(1.中南大学 土木工程学院，湖南 长沙 410075;2.中国建筑第五工程局有限公司，湖南 长沙 410004;3.山东省建筑科学研究院，山东 济南 250031)

自平衡试桩法桩基承载力等效转换新方法

谭现江1，杨高尚1，雷明锋1,2，陈树林3，李玉峰1，2

(1.中南大学 土木工程学院，湖南 长沙 410075;2.中国建筑第五工程局有限公司，湖南 长沙 410004;3.山东省建筑科学研究院，山东 济南 250031)

在分析自平衡试桩法桩基荷载传递机制的基础上，提出一种新的自平衡试桩法桩基承载力等效转换方法。该方法首先基于Mindlin公式求出桩侧摩阻力在桩周和桩底土体中引起的附加应力，通过考虑附加应力对桩侧土体极限侧摩阻力和桩-土界面初始剪切刚度的影响，并采用双曲线模型模拟桩-土界面剪切模量在桩基沉降过程中的动态变化来改进传统的剪切位移等效转换方法，使其适用于大变形的桩基沉降计算。进而，进一步通过对自平衡试桩法测试数据的反演分析，得到土体初始参数，从而转换获得等效的桩基在静载作用下的荷载-沉降曲线，并以此确定桩基承载力。该方法考虑土体的分层性、非线性、连续性和附加应力的影响，避免了在等效转换过程中引入经验系数。实例分析表明，该方法较既有规范中推荐的精确转换法具有更高的精确性，实际工程应用中，能够充分发挥桩基的实际承载能力。

自平衡试桩法；剪切位移法；附加应力；动态模量

自平衡试桩法由于不需要额外的静载压重平台或锚桩反力系统，能够适用于各种试验场地和大吨位桩基，具有试验方便和费用低廉等优点，因此，在国内外逐渐得到广泛应用。然而，由于自平衡试桩法和桩基正常工作时的受力机理不同，因此，在确定桩基承载力时需要将其测试结果进行等效转换。常用的等效转换方法有等位移法、等荷载法、简化法、精确法、解析法和数值计算法[1-5]等。其中，精确法相对于简化法解决了刚性桩身的假定，使其适用性更广，转换结果也更为准确、精度更高[14]。我国交通部于2009年颁布实施的《基桩静载试验自平衡法》(JT/T738)中，就推荐了该方法，在业内也得到了较为普遍的应用。但精确转换法同样存在一定的不足，如在其理论推导过程中，假定桩侧摩阻力仅与该点的位移有关，忽略了土体的连续性，与桩基的实际受力状况不符，尤其是当桩身较长时，其计算误差较大[8]。为此，部分学者通过研究，对该方法进行了改进，分别提出了考虑土体连续性，更加符合荷载传递规律的自下而上[8]和自上而下[9]的迭代计算方法。事实上，上述改进后的2种方法仍然仅仅考虑了土体位移的连续性对桩端的影响，而并没有考虑桩侧土体之间应力的传递以及附加应力对土体参数的影响，因此，改进后方法所得的桩基承载力结果均比不考虑土体连续性时小，很大程度上不能充分发挥桩基的承载能力。可见，尽管自平衡试桩法在试验方法的实现上具有较大的优越性，但对其试验结果的分析以及桩基承载能力的确定仍存在较大的不足，有必要开展深入研究。在对自平衡试桩法桩-土受力机制详细分析的基础上，通过全面考虑桩侧与桩底土中应力的连续性以及附加应力对土体参数的影响，对剪切位移法进行改进，从而试图提出一种新的自平衡试桩法桩基承载力等效转换方法。

1 自平衡试桩法

自平衡试桩法和传统试桩法的荷载传递规律不同，土体的受力机制也不相同。传统试桩法和桩基正常服役时的受力模式相同如图1(a)所示，即荷载作用于桩身顶部，上部桩身首先受压，其荷载一部分沿桩身传递到下部桩体，一部分随着桩身的压缩沉降产生桩侧摩阻力，桩侧摩阻力对下部土体产生附加应力，增加了土体的有效应力。根据Chandler的研究可知，随着有效应力的增加，桩侧极限摩阻力也在增加[10]。又由SSI试验结果表明，随着有效应力的增加，桩-土界面的初始剪切模量也逐渐增大[11-12]。由此可见，考虑土体连续性以及桩侧土产生的附加应力对于桩侧承载力具有提高的效果，同时由于附加应力的存在，桩端的实际受力也将大于桩底的轴力，对桩端承载力具有减小的作用。

(a)传统试桩法；(b)自平衡试桩法图1 桩基承载力试验原理图Fig.1 Experimental principle of pile bearing capacity

而自平衡试桩法则是将荷载箱放置在桩体平衡点位置进行上下加载，如图1(b)，下部桩的荷载传递规律与传统试桩法相同，但上部桩在推力作用下首先克服一部分自重，同时上段桩的下部分受到压缩，一部分荷载向上传递，一部分荷载产生桩侧摩阻力，且方向与自重相反，减小了土体的有效应力，土体的极限侧摩阻力和初始剪切模量都随之减小。相对于传统试桩法，其测得的桩侧摩阻力较小，上段桩桩侧土产生的附加应力对于桩的承载力具有减小的效果。

通过上述分析有，qs1>qs3>qs2和qb1>qb2，这是由桩侧附加应力和桩材泊松比综合效应所导致的结果[15]。因此，采用“精确转换法”时，因未考虑土体的连续性和附加应力的影响，自平衡测试法所得的侧摩阻力—桩土相对位移关系与传统试桩法相同的假定将产生较大误差，不能准确反映桩基的实际承载能力。

2 剪切位移法

剪切位移法最初由Cooke提出的，该方法认为：在荷载水平较低时，桩周剪应力从桩侧表面沿径向向四周扩散到周围土体中，若假定桩侧上下土层之间没有相互作用，即桩-土之间没有相对位移，于是便可建立剪切位移法的基本计算方法[6]，如图2。

(a)整体模型；(b)局部模型图2 剪切位移模型Fig.2 Shear displacement model

根据剪切位移法理论的假定，可用轴对称坐标系建立桩周土的竖向平衡微分方程：

(1)

由于桩体受荷载后桩侧附近竖向应力增量σz相对较小，此处可忽略∂σz/∂z项。由此可求得剪应力在径向的传递方程：

(2)

式中：r0为桩半径；τ0为桩侧表面处的剪应力。

由弹性理论和Cooke假定[6]可得，

(3)

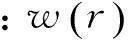
由式(2)～(3)以及桩-土之间不发生相对位移的假设可得：

(4)

该理论在小变形情况下是合适的，Cooke本人所做的试验也证明了这些假定的合理性[6]。

3 剪切位移法的改进

通过前述分析可见，对于既有的剪切位移法在小变形情况下具有较好的适用性，而事实上，桩基在试验以及实际承载过程中，桩周土体均为产生大变形，因此，仅仅采用既有的剪切位移法，得到的结果往往存在较大的误差。为此，笔者通过对剪切位移法的改进，以期建立一种能够用于计算大变形，且可以考虑土体整体连续性的自平衡试桩法桩基承载能力的等效转换方法。

3.1 基本假定

为便于推导和简化分析，做出如下假定：

1)忽略桩身材料泊松比对桩侧摩阻力的影响以及自平衡试桩法中上段桩和下段桩之间的相互影响。

2)单层土体沉降过程符合双曲线模型[13]：

(5)

式中：k0为桩-土界面的初始剪切刚度；τf为桩-土界面的极限抗剪强度。

3.2 改进后的桩侧承载力计算

根据假定(2)，可通过式(4)求得桩土界面的初始剪切刚度k0：

(6)

式中，G0为土体的初始剪切模量。

实际工程上，桩侧土体为非单一土层，且各土层之间在桩基承载过程中会相互影响，产生附加应力。而附加应力又会导致桩-土界面初始剪切刚度及土体极限抗剪强度的改变，因此，需进一步确定该附加应力。

(7)

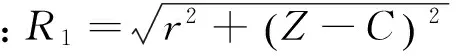
图3 土体附加应力计算模型Fig.3 Additional stress calculation model of soil

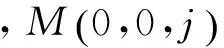
(8)

由此，可分别计算出桩侧土体中附加应力对土体的初始刚度和极限抗剪强度的影响。

对于桩侧土体的极限抗剪强度τf通常采用Chandler提出的有效应力法[10]来确定，即，

(9)

式中：λ0土水平侧压力系数，λ0=1-sinφ′γ′,φ′分别为桩侧土的有效重度和有效内摩擦角；Δσ′为桩侧土附加应力引起的有效应力的增量。

而对于桩侧土的初始剪切刚度k0可将理想弹塑性模型与传统双曲线模型结合考虑，如图4。

理想弹塑性模型和双曲线模型采用相同的界面初始剪切模量，因此，理想弹塑性模型的曲线就是传统双曲线模型的外包线。根据SSI试验[11-12]，桩-土界面的极限相对位移一般为几个毫米，对于同一土层，极限位移变化相对较小，故可对同一土层的极限位移采用一定值Δcr表示。当桩侧土体受附加应力的影响，极限抗剪强度τfΔτf时，土体的初始剪切模量G0ΔG0，进而，由理想弹塑性模型可得：

(10)

图4 桩土界面初始剪切刚度的确定Fig.4 Determination of initial shear stiffness for pile-soil interface

由式(5)和式(10)可知，桩侧土体的初始剪切刚度k0和极限抗剪强度τf具有相同比例的增长。桩—土界面初始模量就反映了随着地基土附加应力的增大而增大的特点。通过反复迭代，即可求得桩侧土体系在任意沉降下考虑附加应力之后的模量。

3.3 改进后的桩端承载力计算

对于桩端承载力的计算，通常采用Randolph解[7]，但当考虑桩侧土体附加应力对桩端的影响时，不同于文献[8-9]采用的位移叠加方式，而是采用应力叠加法，即假定桩端为刚性墩，于是有其沉降量Sb计算表达式为：

(11)

由式(11)可得桩端刚度为：

(12)

考虑桩端的非线性，本文采用非线性割线模量，即桩端的刚度为：

(13)

式中：Pf为桩底土破坏时的极限承载力；Rf为破环比，取0.85。

4 桩基承载力等效转换计算方法

首先综合考虑土体的分层特征，按等长度将桩土结构分成n个单元，并根据杆件的刚度矩阵通过叠加形成桩的整体刚度矩阵；然后根据式(6)建立桩侧土体刚度矩阵以及式(12)～(13)建立桩端土体刚度矩阵；将桩、桩侧土体和桩端土体刚度矩阵进行叠加，形成桩-土体系的总刚度矩阵。

4.1 桩单元

桩单元的刚度矩阵p：

(14)

叠加形成桩身整体刚度矩阵P：

(15)

4.2 桩侧土体单元

土体的刚度矩阵为S：

(16)

4.3 桩端土体单元

桩端土的刚度矩阵为D：

(17)

式中，当i=j=n时，对应的矩阵位置数值为K，其余皆为0。

4.4 桩-土体系刚度矩阵

将式(15)～(17)所示的桩身、桩侧土体和桩端土体刚度矩阵叠加即可得到桩-土体系刚度矩阵PSD，即：

PSD=P+S+D

(18)

4.5 桩体沉降计算

当桩体承受荷载N(i)时，桩体各点的沉降量为s(i)，即

N(i)=PSD(i,j)×s(i)

(19)

由此可求得桩体在任意荷载作用下的沉降量。

图5 反分析Fig.5 Back analysis

4.6 数值求解

由式(19)求解桩体沉降时，还应满足式(5)所示的边界条件。于是，通过分级加载和循环迭代，使每级荷载结果均满足式(5)所示的边界条件，即可求得桩基在每级荷载作用下的沉降。整理前述推导公式，并采用MATLAB编程，即可得到自平衡试桩法桩基承载能力改进后的等效转换结果。

编程过程中，包含式(20)所示方程组的求解和迭代。计算步骤主要有：

1)首先根据自平衡实测的上下段Q～S曲线，反分析确定土体的初始参数，如图5。

2)然后，根据确定的土体初始参数计算桩基的极限承载力，如图6。

(20)

图6 桩基沉降求解Fig.6 Solution for settlement of pile foundation

5 实例分析

金湖湾二期工程桩基为挤压性扩孔混凝土灌注桩，混凝土等级为C40，桩径600 mm，桩长17.5 m。为验证本文方法的可靠性，分别进行自平衡试桩法试验结果的“精确转换法”、改进的剪切位移转换法(即本文考虑土体连续方法)和本文不考虑土体连续的转换法(即不计算附加应力的影响)等效计算，并与静载试桩结果经行对比分析。计算参数如表1，结果对比如图7。

表1 计算参数表Table 1 Parameters of soils

图7 等效转换对比图Fig.7 Comparison of results

从中分析可见：

1)各方法荷载-沉降曲线形态比较一致，均属于陡变型。

2)采用本文方法且考虑土体连续性的桩基承载力计算结果大于“精确转换法”得到的等效荷载，且与实测静载值更为接近；而采用本文方法且不考虑土体连续性时的结果与“精确转换法”得到的等效荷载几乎一致。可见相对于既有的规范方法，本文方法更能精确地计算得到桩基的实际承载能力，对于充分发挥桩基承载能力，降低工程造价具有重要意义。

3)由于本文在考虑土体连续性时以应力为主线，同时考虑了附加应力对桩侧土和桩端土的影响，其结果相对于文献[8-9]只考虑土体连续性对桩端的影响所得的结果不降反增，比“精确转换法”所得的极限承载力提高了16%，也更接近于实测的桩基静载极限承载力。

6 结论

1)在分析自平衡试桩法桩基荷载传递机制的基础上，基于Mindlin公式求出桩侧摩阻力在桩周和桩底土体中引起的附加应力。分别通过考虑附加应力对桩侧土体极限侧摩阻力和桩-土界面初始剪切刚度的影响，以及采用双曲线模型模拟桩-土界面剪切模量在桩基沉降过程中的动态变化对传统的剪切位移等效转换方法进行了改进，提出一种考虑土体的分层性、非线性、连续性和附加应力的影响自平衡试桩法桩基承载力等效转方法。

2)改进后的自平衡试桩法桩基承载力等效转方法首先通过自平衡试桩法测试数据的反演分析，得到土体初始参数，进而转换获得桩基在静载作用下的荷载-沉降曲线，并以此确定桩基承载力，弥补了规范推荐方法——精确转换法计算过程中需引入经验系数的不足。

3)实例分析表明，等效转换过程中，是否考虑土体的连续性对桩基的承载力分析结果影响较大。当同时考虑因土体连续性而产生的附加应力对桩侧土和桩端土的影响时，其结果比仅考虑对桩端影响时所得的结果大，同时与规范中推荐的精确转换法所得的桩基极限承载力相比，提高了16%，且更接近实际静载测试结果。可见，该方法较既有规范中推荐的精确转换法具有更高的精确性，实际工程应用中，能够充分发挥桩基的实际承载能力。

[1] 鲍育明,刘亚文,李志成,等.自平衡法在桩基承载力检测中的应用[J]. 解放军理工大学学报(自然科学版),2003,4(3):49-52. BAO Yuming, LIU Yawen, LI Zhicheng, et al. Application of self-balanced method for pile bearing capacity test [J]. Journal of PLA University of Science and Technology, 2003, 4(3): 49-52.

[2] 龚维明,戴国亮，蒋永生，等.桩承载力自平衡测试理论与实践[J]. 建筑结构学报, 2002, 23(1): 82-88. GONG Weiming, DAI Guoliang, JIANG Yongsheng, et al.Theory and practice of self-balanced loading test for pile bearing capacity [J]. Journal of Building Structures, 2002, 23(1): 82-88.

[3] 郑英杰, 张克绪, 张尔其, 等. 由O-cell试桩结果确定整桩的性能[J]. 岩土工程学报, 2008, 30(9): 1416-1422. ZHENG Yingjie, ZHANG Kexu, ZHANG Erqi, et al. Determination of pile behaviors based on o-cell test results of piles [J]. Chinese Journal of Geotechnical Engineering, 2008, 30(9): 1416-1422.

[4] 蒋益平,杨敏,熊巨华.自平衡试桩荷载-沉降曲线的解析算法[J]. 岩石力学与工程学报, 2006, 25(增1): 3258-3264. JIANG Yiping, YANG Min, XIONG Juhua. Analytical equation of loading-settlement curve under O-cellpile testing method [J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(Suppl 1): 3258-3264.

[5] 熊巨华, 蒋益平, 杨敏. 自平衡试桩结果的解析转换法[J]. 同济大学学报(自然科学版),2007, 35(2): 161-165. XIONG Juhua, JIANG Yiping, YANG Min. Analyticalsolution transformation method for data of O-cell pile testing [J]. Journal of Tongji University (Natural Science), 2007, 35(2): 161-165.

[6] Cooke R W, Price G, Tarr K. Jacked piles in London Clay: a study of load transfer and settlement under working conditions[J]. Geotechnique, 1979, 29(2): 113-147.

[7] Randolph M F, Wroth, C P. Analysis of deformation of vertically loaded piles [J]. Journal of the Geotechnical Engineering Division, 1978, 104(12): 1465-1488.

[8] 马远刚, 朱艳. 基于改进荷载传递函数的自平衡数据转换[J]. 桥梁建设, 2005(B6): 142-144. MA Yuangang, ZHU Yan. Conversion of self- balanced load test data based on improved load transfer function [J]. Bridge Construction, 2005(B6): 142-144.

[9] 朱向荣, 汪胜忠, 叶俊能, 等. 自平衡试桩荷载传递模型及荷载-沉降曲线转换方法改进研究[J]. 岩土工程学报, 2010, 32(11): 1717-1721. ZHU Xiangrong, WANG Shengzhong, YE Junneng, et al. Load transfer model and improved transition method for load-settlement curve under O-cell pile testing method [J]. Chinese Journal of Geotechnical Engineering, 2010, 32(11): 1717-1721.

[10] Chandler R J. The shaft friction of piles in cohesive soils in terms of effective stress [J]. Civil Engineering and Public Works Review, 1968, 63:48-51.

[11] Yin Z Z, Zhu H, Xu G H. A study of deformation in the interface between soil and concrete [J]. Computers & Geotechnics, 1995, 17(1):75-92.

[12] Desai C S, Mm E C, Zaman M M. Cyclic testing and modeling of interfaces[J].Journal of Geotechnical Engineering, 1985, 111(6):793-815.

[13] 吴军帅, 姜朴. 土与混凝土接触面的动力剪切特性[J]. 岩土工程学报, 1992, 14(2):61-66. WU Junshuai, JIANG Pu. Dynamic shear properties of soil-concrete interface [J]. Chinese Journal of Geotechnical Engineering, 1992, 14(2):61-66.

[14] 程宝辉. 自平衡试桩法极限承载力不同计算方法计算结果的对比分析[J]. 桥梁建设, 2009(2): 23-26. CHENG Baohui. Comparative analysis of calculation results of ultimate bearing capacity of pile self- balanced load test according to different calculation methods [J]. Bridge Construction, 2009(2): 23-26.

[15] 聂如松,冷伍明,杨奇,等.桩-土间剪切应力的传递探讨[J]. 岩土力学, 2009, 30(3): 799-804. NIE Rusong, LENG Wuming, YANG Qi, et al. Discussion on shear stress transfer between pile and soil [J]. Rock and Soil Mechanics, 2009, 30(3): 799-804.

A new equivalent transformation method for calculatingthe pile bearing capacity on self-balancing test results

TAN Xianjiang1, YANG Gaoshang1, LEI Mingfeng1,2, CHEN Shulin3，LI Yufeng1,2

(1.School of Civil Engineering, Central South University, Changsha 410075, China;2. China Construction Fifth Engineering Division Co. Ltd.,Changsha 410004, China;3.Shandong Provincial Academy of Building Research, Jinan 250014, China)

By analyzing the load transfer mechanism of pile foundation, a new method of equivalent conversion of self-balanced test piles is proposed. Firstly, the additional stress caused by the friction of the pile side friction in the soil around the pile and the bottom of the pile is obtained based on Mindlin formula. And the influence of additional stress on the ultimate lateral friction of the pile side soil and the initial shear stiffness of the pile soil interface is considered. The dynamic changes of the shear modulus of the pile and soil interface in the process of pile foundation settlement are simulated by using the hyperbolic model used to calculate the large deformation of the pile foundation settlement. By analyzing the test data of the self-balanced test pile, the initial parameters of the soil are obtained, and the load bearing capacity of the pile foundation under static load is also determined. In this method, the effect of the layered, nonlinear, continuous and additional stress of soil are considered, and the empirical coefficient is avoided. The example analysis shows that the proposed method has higher accuracy than the precise conversion method, which can enhance the actual bearing capacity of the pile foundation.

self-balanced test method on pile; shear displacement method; additional stress; dynamic modulus

2016-01-29

国家自然科学基金资助项目(51508575)；中国博士后科学基金资助项目(2014M560652，2016T90764)；湖南省创新平台与科技人才资助项目(2015RS4006)

雷明锋(1982-)，男，湖南祁东人，讲师，博士，从事隧道与地下工程方面的教学与科研；E-mail:124520238@qq.com

TU473

A

1672-7029(2016)12-2388-08