高速列车前端吸能结构理论预测与数值模拟

张秧聪，许平，姚曙光，邓雯苑,2

(1．中南大学 轨道交通安全教育部重点实验室，湖南 长沙 410075；2．广东技术师范学院 汽车学院，广东 广州 510000)

高速列车前端吸能结构理论预测与数值模拟

张秧聪1，许平1，姚曙光1，邓雯苑1,2

(1．中南大学 轨道交通安全教育部重点实验室，湖南 长沙 410075；2．广东技术师范学院 汽车学院，广东 广州 510000)

基于简化基本折叠单元理论，3种截面构型的高速列车前端吸能结构的横截面分为V形、Y-I形和Y-II形3种基本角单元，对其轴向压缩平均载荷进行理论求解。为验证理论预测公式的可靠性，采用基于LS-DYNA的非线性有限单元法对3种吸能结构进行数值模拟，并与理论结果进行比较。在此基础上，研究五元胞组合蜂窝管的单元胞边长和壁厚2个参数对其耐撞性的影响。研究结果表明：3种吸能结构的平均载荷理论预测值与数值仿真值相差不大，其中五元胞组合蜂窝管耐撞性最好，其平均载荷是壁厚的1.5次幂函数，是单元胞边长的0.5次幂函数，增加壁厚能显著提高平均载荷，比吸能是壁厚的0.5幂函数，是单元胞边长的负0.5次幂函数。

高速列车；耐撞性；理论预测；有限元；参数研究

随着高速列车运行速度的提升，携带的动能也大幅提高[1]，一旦发生碰撞事故，会造成无法挽回的人员伤亡和巨大的经济损失，因此，提高高速列车吸能装置的耐撞性非常重要。理想的吸能结构应在可控制的变形区域内发生塑性变形，吸收撞击动能，同时保障乘客区域不发生严重破坏[2]。对于高速动车组来说，采用薄壁管吸能构件是比较合适的。国内外学者已经在列车吸能结构方面做了很多工作并取得了一定成果[3-9]，其中，在薄壁吸能构件方面，舒东等[10-13]对吸能结构中常用的典型薄壁结构碰撞吸能的影响因素如结构横截面形状、结构尺寸、材料特性参数、结构预变形等对结构碰撞吸能特性的影响规律进行了研究；高广军等[14]对六边形蜂窝结构进行了数值仿真，发现组合构型多胞管的吸能特性优于单胞管。蜂窝型薄壁构件因其吸能效率高、重量轻、成本低等特点，被广泛应用于车辆轮船、航空航天等领域，其吸能能力由平均载荷及压缩行程决定。要提高蜂窝管的耐撞性，在动车组车体有限的安装空间下，增加其平均载荷是简单有效的方法。因此，有必要在设计初期，从理论方面定量研究蜂窝管的平均载荷及其影响因素。在理论预测方面， Mcfarland[15]最早计算了正六边形蜂窝的平均载荷，之后Wierzbicki等[16]基于超级折叠单元理论(SFE)，推导出正六边形蜂窝的轴向平均载荷和折叠波长理论公式，但是公式十分复杂。为了将SFE理论应用到多胞管，Chen等[17]提出了简化的超级折叠单元理论(SSFE)，计算了多胞管的折叠波长和平均载荷的理论表达式，并通过有限元法验证了理论解的准确性。根据Chen等[17]研究显示，多胞管与其相对应的单胞管相比，比吸能可以提高大约15%。尹汉峰等[18]也采用SSFE方法对三种常用蜂窝结构的轴向平均载荷进行了理论计算和耐撞性优化设计，发现正六边形蜂窝结构耐撞性最好。实际应用中蜂窝胞元构型有很多种，而Wierzbicki的SFE理论仅能求解正六边形蜂窝管准静态下轴向平均载荷，对于组合截面构型的多胞蜂窝管则无法求解。基于前人的研究，蜂窝型多胞吸能结构具有广泛的应用前景。本文以实际工程项目为背景，在动车组前端吸能结构前期结构设计阶段，基于简化的基本折叠单元理论对三种截面构型多胞蜂窝管的平均轴向载荷进行理论预测，从中选出最优截面构型的多胞蜂窝管。基于非线性有限元软件LS-DYNA，建立此吸能结构的有限元模型，通过数值模拟验证平均载荷理论公式的准确性。进而对多胞蜂窝管进行参数研究，分析胞元尺寸和壁厚对其力学特性的影响，从而为高速列车端部吸能结构的前期结构设计和后期优化分析提供指导。

1 高速列车前端吸能结构理论预测

以国产某型号动车组前端吸能结构为研究对象，包括四元胞、五元胞和五元胞组合3种截面构型多胞蜂窝管，其横截面如图1所示，安装面长和宽限定为280 mm×245 mm，单元胞边长为a，整个吸能薄壁管的壁厚为t，其中a=56 mm，t=5 mm。这里运用简化的超级折叠单元理论模型(SSFE)解决高速列车多胞蜂窝管能量吸收理论预测问题，将3种构型的多胞蜂窝管分为3种基本角单元：V形基本角单元、 Y-I形单元和Y-II形单元。

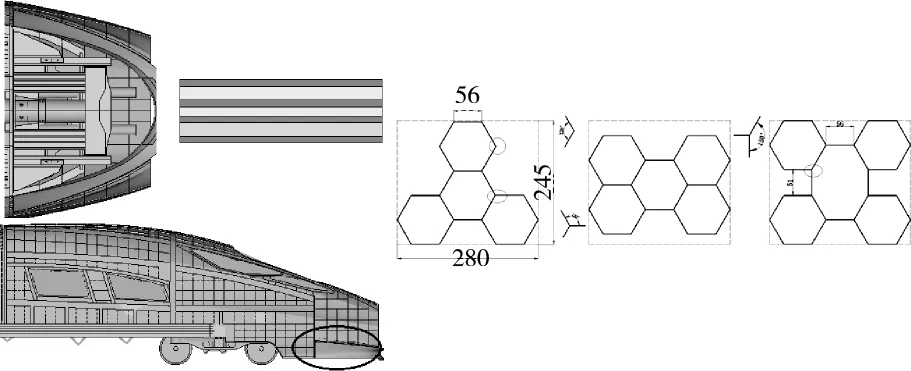
图1 高速列车前端吸能结构Fig.1 High-speed train front-end energy-absorbing structure

根据能量守恒原理，高速列车多胞蜂窝管轴向压缩吸能为

(1)

其中：Pm，2H，Eb和Em分别为平均压溃力、折叠波长、弯曲变形能和薄膜变形能；η为有效撞击距离系数。由于薄壁结构的厚度和S型折叠压不实等因素，实际撞击位移要小于2H，Abramowicz等研究发现有效撞击距离系数η的取值范围为在0.7～0.75[16]比较合理，所以本文中取η为0.75。

1.1 弯曲变形能

根据SSFE理论，假设壁厚恒定且屈曲波长保持为2H，分析多胞蜂窝管的能量耗散，每个基本角单元的吸能区可以分为3个延展性三角单元组成的薄膜变形区(图2(a))及3个弯曲绞线组成的弯曲变形区(图2(b))。

(a)薄膜变形区；(b)弯曲变形区；(c)弯曲绞线和旋转角图2 变形区Fig.2 Zone

(2)

其中：B0为组成基本角单元的胞壁边长之和。

1.2 薄膜变形能

在一个折叠波长中，每块翼缘板的薄膜变形能Em可以通过对图2(a)的三角形单元的面积积分估算。即

(3)

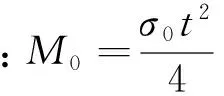
(4)

其中：σy和σu分别代表材料的屈服应力和极限应力；n代表应变硬化指数。根据Zhang的研究，假设每块板的作用相似，直角单元的薄膜变形能就是一块板的能量消耗的2倍，即

(5)

由图3可得V形单元的薄膜变形能为

(6)

Y-Ⅰ形单元可以看作是由一个V形单元和一块附加板组成，Y-Ⅱ形单元可以看作由一个直角单元和一块附加板组成，如图4。其中附加板的薄膜变形能为

(7)

图3 直角单元和V形角单元Fig.3 Right corner element and V angle element

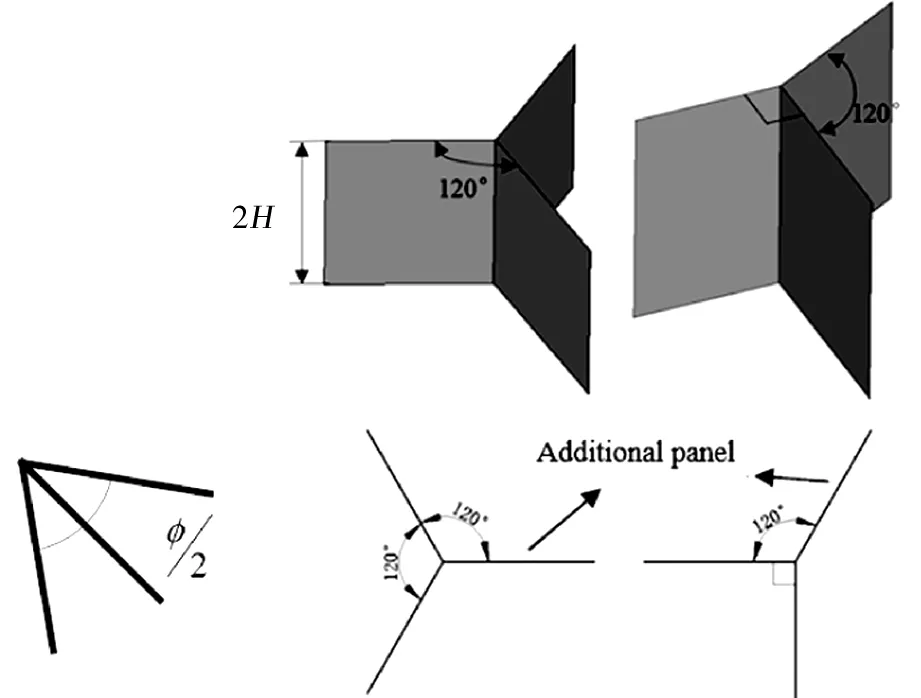
图4 Y形角单元Fig.4 Y angle element

所以Y-Ⅰ和Y-Ⅱ形单元的薄膜变形能分别为

(8)

(9)

1.3 平均载荷的理论预测

如图1所示，五元胞组合截面构型蜂窝管由16个V形单元、4个Y-I形单元和4个Y-II形单元构成，将等式(2)，(6)，(8)和(9)代入式(1)中，可得

(10)

求解可得五元胞组合蜂窝管的平均载荷为

(11)

同理可得四元胞和五元胞蜂窝管的平均载荷理论预测公式，如表1所示。

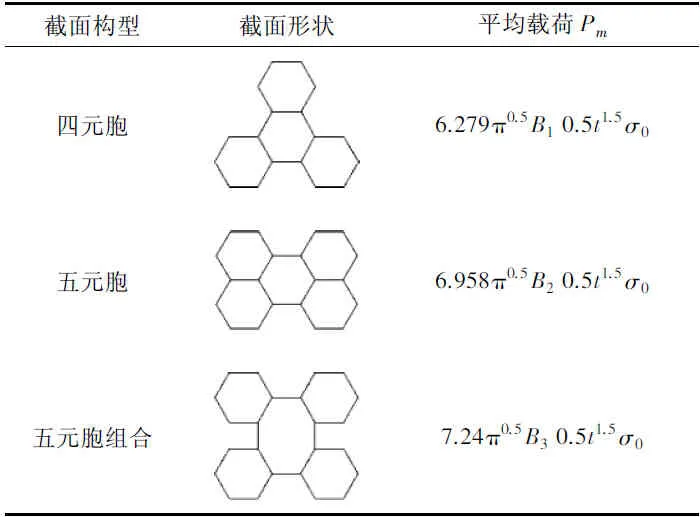
表1 多胞蜂窝管特性Table 1 Characters of multi-cell honeycomb tubes

2 高速列车吸能结构的数值模拟

为验证高速列车吸能结构平均载荷理论预测公式的准确性，采用非线性有限元软件LS-DYNA，对五元胞组合截面构型的蜂窝管进行数值模拟。

2.1 有限元模型

分别选取300 mm长的3种多胞蜂窝管，单元胞边长a均为56 mm，壁厚t为5 mm，有限元网格密度为5 mm×5 mm，用四节点壳单元建模。薄壁管和刚性墙之间的接触定义Automatic_Nodes_to_Surface，表面的摩擦因数设为0.3。蜂窝管和端板定义Automatic_Single_Surface模拟真实的表面接触，避免在轴向压缩过程中产生穿透。为了产生足够的动力，端板附加总重1 000 kg的质量点，蜂窝管和端板以10 m/s的初速度冲击刚性墙，计算模型如图5所示。

图5 有限元模型及边界条件Fig.5 FEM and boundary conditions

2.2 材料模型

吸能结构的材料为6008系铝合金，为了获得材料特性参数，从吸能结构上截取一块标准件，在MTS 647液压万能材料试验机进行准静态拉伸试验，如图6所示，因金属材料在弹性阶段应力随应变呈线性变化，试验时采用恒定载荷增量加载以缩短加载时间，加载载荷增量为20 kN/min；当进入初始塑性后，采用15 mm/min的恒定速度加载。得到材料的应力-应变曲线如图7所示，材料的参数如表2所示，使用LS-DYNA材料库的中“Mat.024-MAT_PIECEWISE_LINEAR_PLASTICITY”材料模型定义6008系铝合金的材料属性。根据公式(4)求得6008系铝型材的流动应力σ0=132.929 MPa。

表2 吸能结构材料参数Table 2 Energy-absorbing structure material properties

图6 准静态拉伸试验Fig.6 Quasi-tensile test

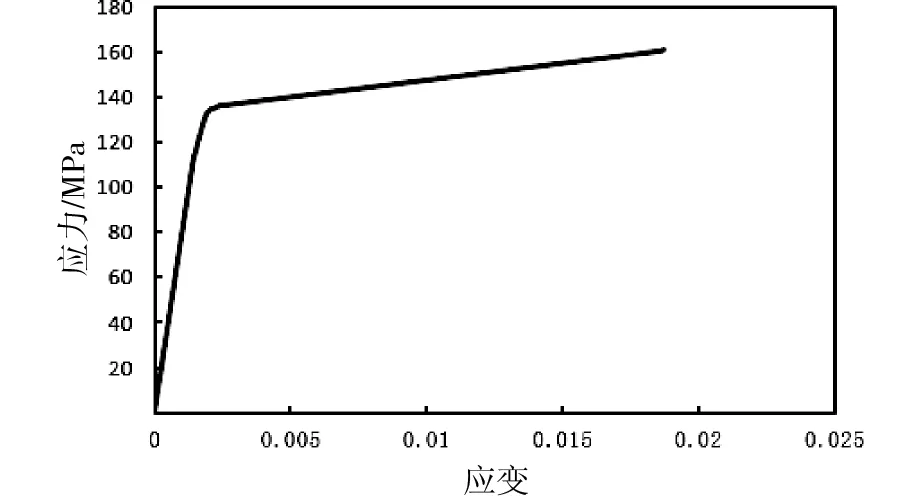
图7 材料拉伸试验数据Fig.7 Tensile test data for the material

2.3 计算结果

实际运用中，薄壁构件的轴向压缩载荷是受到动态冲击速度的影响。研究表明[20]，动态压缩载荷一般要比相应的准静态压缩载荷大，其动态增大系数λ为1.3～1.6，且动态增大系数与速度成正比。计算边界条件中速度为10 m/s，取动态增大系数λ为1.3。所以3种蜂窝管修正后的平均载荷预测公式为

(14)

(15)

(16)

多胞蜂窝管变形过程中撞击力-位移曲线见图8，撞击开始后，撞击力首先达到一个峰值，接着急速下降后在平均载荷上下做周期性振荡，最终完成叠缩变形。多胞蜂窝管轴向压缩特性的数值结果和理论结果的对比如表3。从表中发现3种构型的吸能结构平均载荷的数值仿真值和修正后理论预测值基本一致，从而验证了平均载荷理论公式的准确性。在高速列车前端吸能结构安装面积一定的情况下，横截面长和宽为280 mm×245 mm，单元胞边长a和壁厚t都相同，五元胞组合截面构型的蜂窝管平均载荷明显要比四元胞和五元胞大，即吸能结构压缩相同的距离，五元胞组合构型蜂窝管吸能量要比其余两者大得多，所以选择五元胞组合构型蜂窝管作为最优方案。

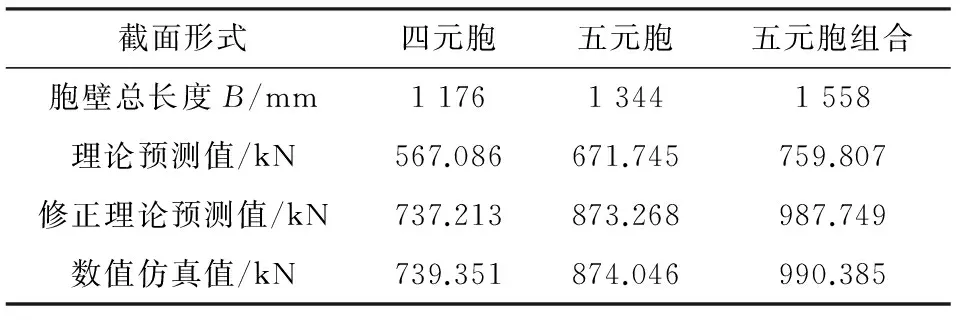
表3 数值结果与理论结果对比Table 3 Comparison of numerical results and theoretical results

图8 撞击力-位移曲线Fig.8 Crushing force-displacement curve

3 高速列车吸能结构耐撞性的参数研究

为研究高速列车吸能结构的耐撞特性，对五元胞组合截面构型的多胞蜂窝管进行参数研究，分析单元胞边长a和壁厚t对其碰撞力学特性的影响。

3.1 评价指标

多胞蜂窝管作为高速列车的主吸能元件时，要求其质量越轻越好，同时吸能效率越高越好，为了估计结构单位质量的能量吸收，定义比吸能SEA[13]为：

(17)其中：EA表示缓冲变形吸收的内能。根据多胞蜂窝管的轴向平均载荷理论预测公式，蜂窝管的轴向平均载荷取决于横截面上的单元胞边长a和壁厚t。

3.2 讨论

为研究胞壁边长a和壁厚t对多胞蜂窝管的平均载荷和比吸能的影响，设计2因素5水平的全因子试验，共25个样本，全因子试验设计及结果如表4所示。

由图9可知，平均载荷Pm的仿真值基本都在理论值曲线附近，两者吻合得很好。在单元胞边长a不变的情况下，平均载荷随着壁厚t的增大而增大，而且变化趋势明显，说明壁厚t对平均载荷的影响显著；平均载荷的仿真值要比理论值偏大，在壁厚t不变的情况下，平均载荷随着单元胞边长a增大而增大，但是变化趋势不明显，说明单元胞边长a对平均载荷的影响不大。这一点也可以从平均载荷理论预测公式(14)看出，平均载荷是单元胞边长a的0.5次幂函数，是壁厚t的1.5次幂函数。另外，胞壁边长不同时，对应的平均载荷-壁厚曲线基本平行，说明平均载荷随壁厚t变化而变化的速率和单元胞边长a没有关系。壁厚t不同时，对应的平均载荷-胞壁边长曲线也基本平行，说明平均载荷随胞壁边长变化而变化的速率和壁厚t无关。

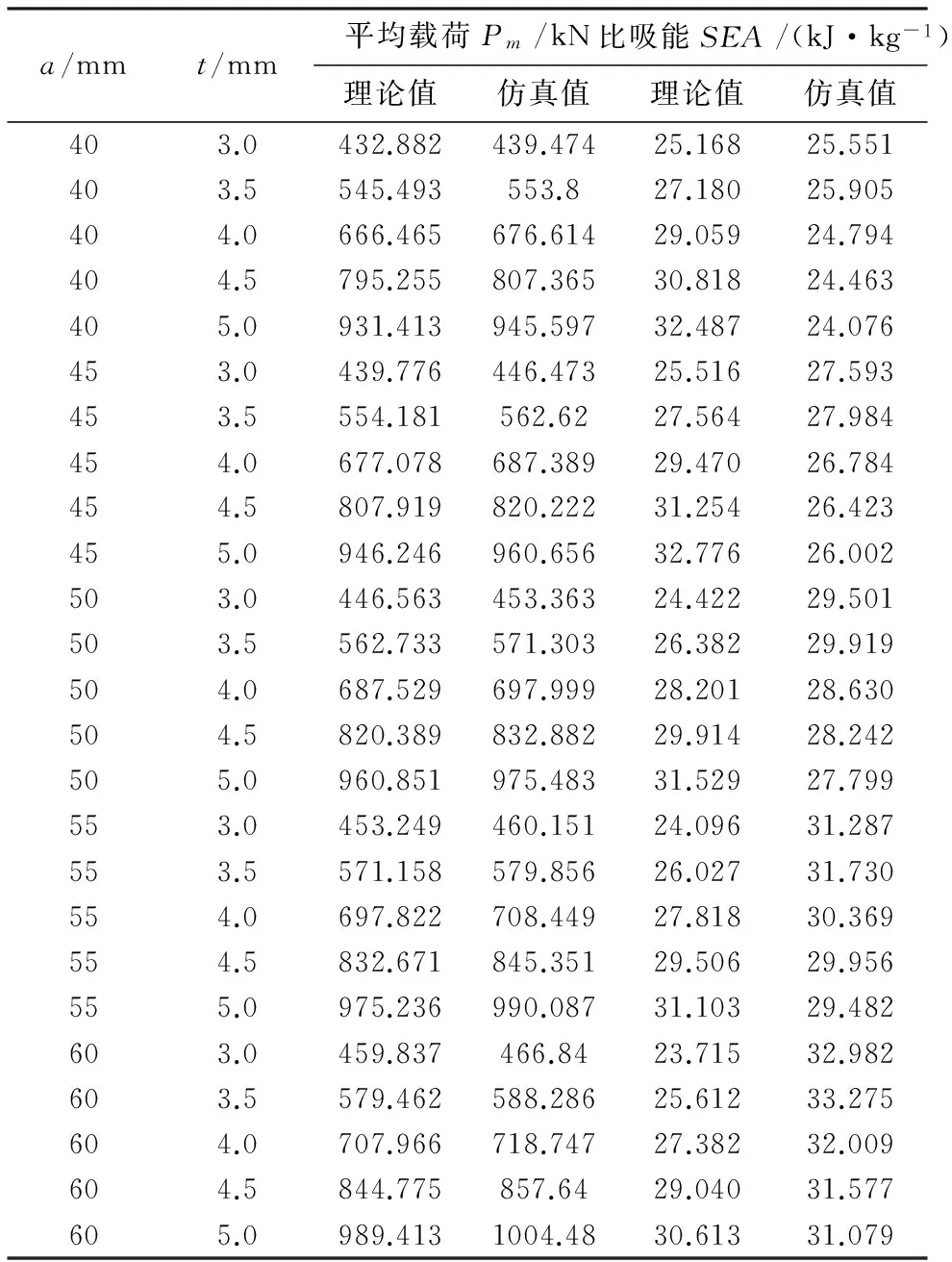
表4 全因子试验设计及结果Table 4 Full factorial experiment design and result

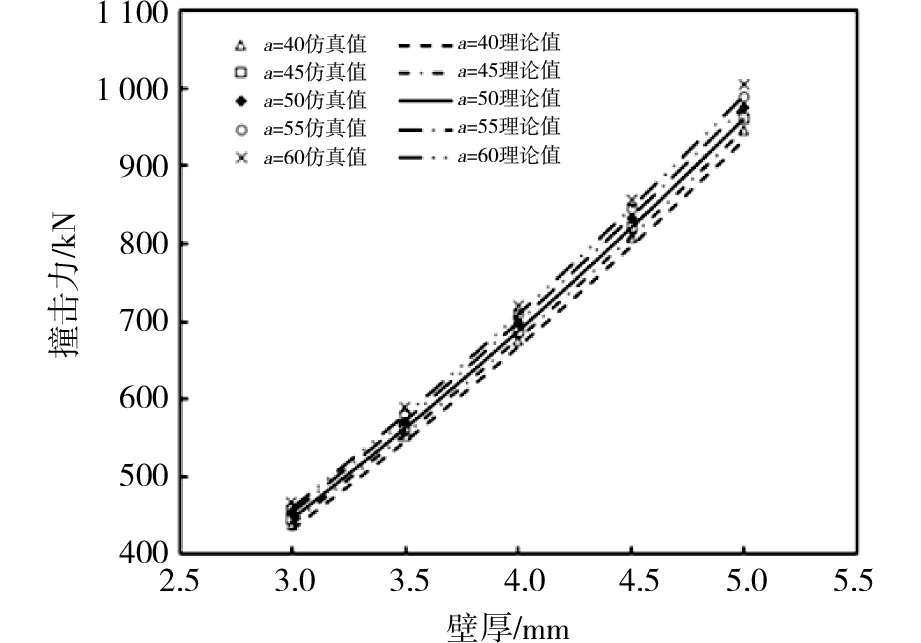
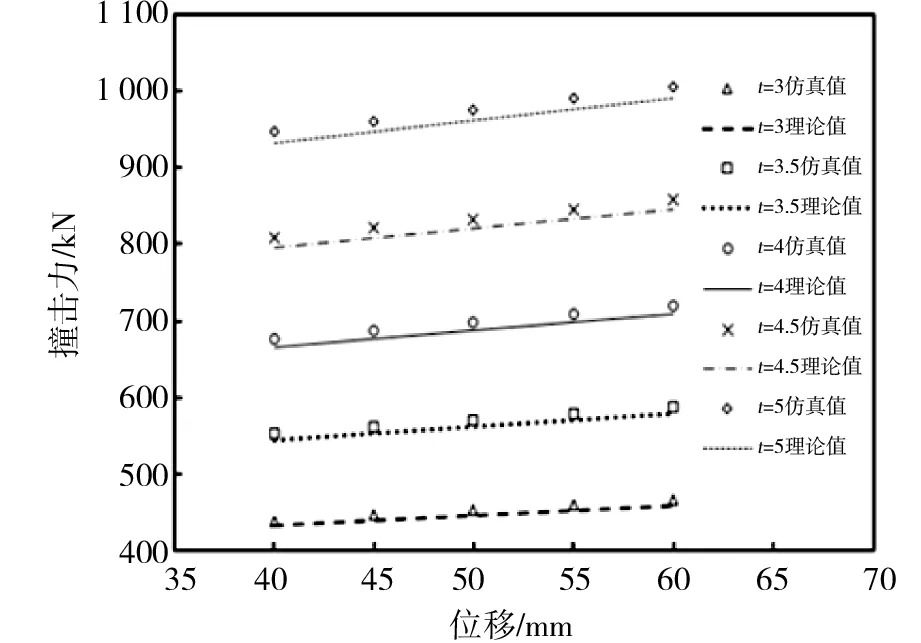
图9 壁厚和单元胞边长对平均载荷的影响Fig.9 Influence of cell-wall length and thickness on the mean crushing force

由图10可知，比吸能SEA的仿真值要比理论值大，但是增加的趋势和理论值一致，当单元胞边长a不变时，随着壁厚t的增大而增大，且趋势明显。当壁厚t不变时，比吸能SEA随单元胞边长a的增大先增大后减小，在单元胞边长a为45 mm时达到最大值。比吸能SEA随着单元胞边长a变化的幅度不是很大，说明相比壁厚t，单元胞边长a对比吸能SEA的影响较小。

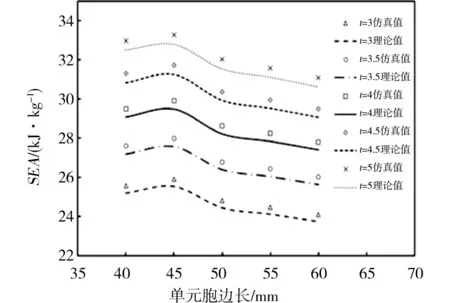
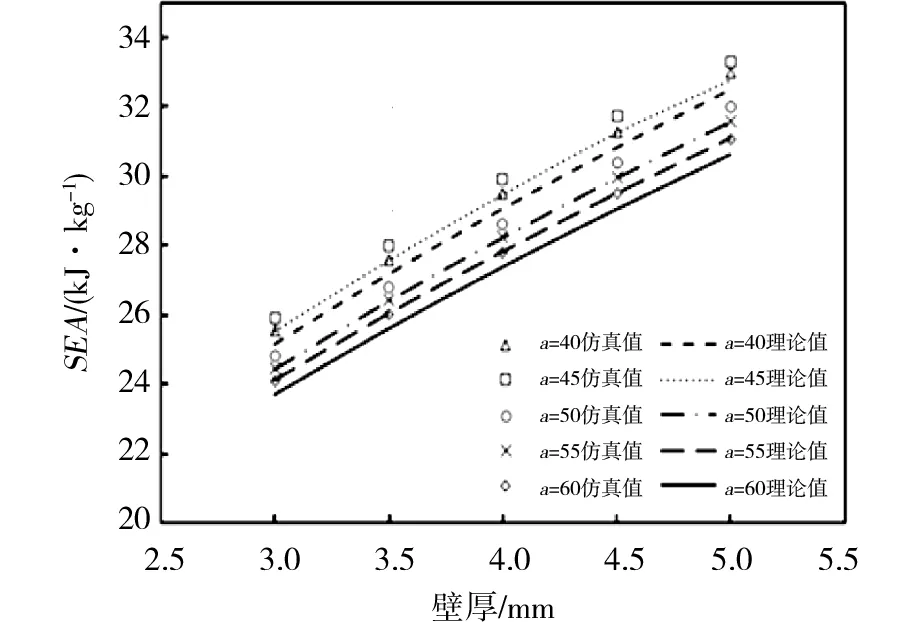
图10 壁厚和单元胞边长对比吸能的影响Fig.10 Influence of cell-wall length and thickness on SEA

4 结论

1)运用简化的超级折叠单元理论模型(SSFE)解决高速列车多胞蜂窝管能量吸收理论预测问题，四元胞、五元胞和五元胞组合截面构型3种多胞蜂窝管横截面被分为V形、Y-I形和Y-II形3种基本角单元，计算三者的平均载荷理论预测公式。

2)为验证理论公式的可靠性，采用非线性有限法对3种多胞蜂窝管轴向压缩进行数值模拟，仿真结果和理论结果吻合很好，多胞蜂窝管的平均载荷理论预测公式是准确的。在相同单元胞边长a和壁厚t的情况下，五元胞组合蜂窝管平均载荷要比四元胞和五元胞大，即五元胞组合蜂窝管能量吸收效率最好。

3)根据理论公式和数值仿真，研究五元胞组合蜂窝管的单元胞边长和壁厚2个参数对其碰撞力学特性的影响，发现多胞蜂窝管的平均载荷是壁厚的1.5次幂函数，是单元胞边长的0.5次幂函数，增加壁厚能显著提高平均载荷；比吸能SEA是壁厚的0.5幂函数，是单元胞边长的负0.5次幂函数。研究结果为高速列车前端吸能结构的初期设计和后期优化分析提供指导，具有工程应用价值。

[1] 张志新, 肖守讷, 阳光武, 等.高速列车乘员碰撞安全性研究[J]. 铁道学报, 2013, 35(10): 24-32. ZHANG Zhixin, XIAO Shoune, YANG Guangwu, et al. Research on collision safety of high-speed train crews & passengers[J]. Journal of the China Railway Society, 2013, 35(10): 24-32.

[2] 刘建新, 赵华. 高速动力车能量吸收装置[J]. 铁道学报, 1997, 19(3): 32-36. LIU Jianxin, ZHAO Hua. Energy absorbing devices for high-speed locomotive under crash[J]. Journal of the China Railway Society, 1997, 19(3): 32-36.

[3] Lewis J H. Structural crashworthiness—possibilities and practicalities[J]. Proceedingsof the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2002, 216(2): 117-121.

[4] Lewis J H, Rasaiah W G, Scholes A. Validation of measures to improve rail vehicle crashworthiness[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 1996, 210(2): 73-85.

[5] Lu G. Energy absorption requirement for crashworthy vehicles[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2002, 216(1): 31-39.

[6] 李松晏,郑志军.高速列车吸能结构设计和耐撞性分析[J]. 爆炸与冲击, 2015(2):164-170. LI Songyan, ZHEN Zhijun. Energy-absorbing structure design and crashworthiness analysis of high-speed trains[J]. Explosion and Shock Waves, 2015(2):164-170.

[7] 雷成, 肖守讷, 罗世辉. 基于显式有限元的高速列车吸能装置吸能原理研究[J]. 铁道机车车辆, 2012, 32(2): 1-5. LEI Cheng, XIAO Shoune, LUO Shihui. Research on the energy-absorbing theory of high-speed train energy-absorbing component based on the explicit finite element[J]. Railway Locomotive & Car, 2012, 32(2): 1-5.

[8] 陈秉智, 张向海, 马纪军, 等.高速动车组被动安全性和耐撞性研究[J]. 计算力学学报, 2011, 28(1): 152-158. CHEN bingzhi, ZHANG Xianghai, MA Jijun, et al. High-speed EMUs passive safety and crashworthiness study[J]. Chinese Journal of Computational Mechanics, 2011, 28(1): 152-158.

[9] 张志新. 高速列车耐撞性结构及安全性研究[D].成都：西南交通大学, 2012. ZHANG Zhixin. Reserach on crashworthy structures and collision safety for high-speed trains[D]. Chengdu: Southwest Jiaotong University, 2012.

[10] 舒冬, 姚松. 基于微分进化算法的列车吸能方管结构耐撞性多目标优化设计[J]. 铁道科学与工程学报, 2011, 8(2): 92-96. SHU Dong,YAO Song. Multi-objective optimization design of train crashworthy tube and analysis of energy absorption based on differential evolution algorithms[J]. Journal of Railway Science and Engineering, 2011, 8(2): 92-96.

[11] 栗荫帅. 车辆薄壁结构碰撞吸能特性分析与改进[D].大连：大连理工大学, 2007. LI Yinshuai. Crashworthiness and encrgy absoption characteristic analyses of thin-walled structures in vehicle body [D]. Dalian: Dalian University of Technology, 2007.

[12] 贾宇, 肖守讷.耐碰撞车体吸能装置的薄壁结构研究[J]. 铁道车辆, 2005, 43(5): 6-10. JIA Yu, XIAO Shoune. Research on the thin-wall structureof the energy absorption equipment on the collision resistant car-body[J]. Rolling Stock, 2005, 43(5): 6-10.

[13] 谢素超. 耐冲击地铁车辆吸能结构研究[D].长沙：中南大学, 2007. XIE Suchao. Research of the energy-absobing structure of crashworthy subway vehicle[D]. Changsha: Central South University, 2007.

[14] 高广军, 姚松. 车辆薄壁结构撞击吸能特性研究[J]. 铁道机车车辆, 2002 (2): 8-10. GAO Guangjun, YAO Song. Research on energy absorption attribute in collision of thin-walled structure between trains[J] . Railway Locomotive & Car , 2002 (2): 8-10.

[15] Mcfarland R K. Hexagonal cell structures under post-buckling axial load [J]．AIAA Journal，1963，l(6)：1380-1385.

[16] Wierzbicki T, Abramowicz W. On the crushing mechanics of thin-walled structures[J]. Journal of Applied Mechanics, 1983, 50(4a):727-734.

[17] Chen W, Wierzbicki T. Relative merits of single-cell, multi-cell and foam-filled thin-walled structures in energy absorption[J]. Thin-Walled Structures, 2001, 39(4):287-306.

[18] 尹汉锋, 文桂林. 基于简化基本折叠单元法的蜂窝耐撞性优化设计[J]. 机械工程学报, 2011(16):93-100. YIN Hanfeng, WEN Guilin. Crashworthiness optimization design of honeycombs based on the simplified basic folding element method[J]. Journal of Mechanical Engineering, 2011(16):93-100.

[19] 张在中, 姚曙光, 许平,等. 高速列车车体前端吸能结构的碰撞仿真与试验[J]. 机车车辆工艺,2015(3):33-34. ZHANG Zaizhong, YAO Shuguang, XU Ping, et al. High-speed train car body front-end energy-absorbing structure of crash simulation and experiment[J]. Locomotive & Rolling Stock Technology, 2015(3):33-34.

[20] Langseth M, Hopperstad O S. Static and dynamic axial crushing of square thin-walled aluminium extrusions[J]. International Journal of Impact Engineering, 1996,18(7): 949-968.

Theoretical prediction andnumerical simulation of thehigh-speed train front-end energy-absorbing structure

ZHANG Yangcong1, XU Ping1,YAO Shuguang1, DENG Wenyuan1,2

(1.Key Laboratory of Traffic Safety on Track of Ministry of Education, Central South University, Changsha 410075, China;2. School of Automotive Engineering, Guangdong Polytechnic Normal University, Guangzhou 510000, China)

Based on the Simplified Super Folding Element theory, the cross section of three kinds of high-speed train front-end energy-absorbing structure were divided into the three different basic angle elements which include V, Y-I and Y-II. The theoretical prediction of the mean crushing force were proposed for the multi-cell honeycomb tubes under axial crushing loading. In order to validate the theoretical solutions, the axial crushing simulation of three kinds of high-speed train front-end energy-absorbing structure were implemented by employing the nonlinear finite element method on the basis of LS-DYNA. Based on the theoretical solutions and the simulation, the influence of the cell-wall length and thickness on crashworthiness was studied, the results show that: The analytical solutions show an excellent agreement with the simulation results. The energy absorption capacity of five-cell combination honeycomb tube is the most excellent among three kinds of energy-absorbing structure. The mean crushing force of multi-cell honeycomb tubes is 1.5 times the power function of thickness and it is 0.5 times the power function of cell-wall length. The increase of the thickness can significantly improve the mean crushing force. The specific energy absorption is 0.5 times the power function of thickness and it is 0.5 times the negative power function of cell-wall length.

high-speed train; crashworthiness; theoretical prediction; FEM; parameter study

2016-02-24

国家自然科学基金重点资助项目(U1334208); 教育部重点资助项目(113051A);国家科技支撑计划项目(2015BAG12B01)

姚曙光(1970-)，女，湖南邵阳人，副教授，从事车辆结构分析研究；E-mail：ysgxzx@csu.edu.cn

U260.2

A

1672-7029(2016)12-2327-08