基于选权迭代法的既有铁路平面线形拟合方法

马洪磊，刘成龙

(1.中铁第一勘察设计院集团有限公司，陕西 西安 710043；2.轨道交通工程信息化国家重点实验室(中铁一院)，陕西 西安 710043；3.西南交通大学 地球科学与环境工程学院，四川 成都 611756)

基于选权迭代法的既有铁路平面线形拟合方法

马洪磊1,2，刘成龙3

(1.中铁第一勘察设计院集团有限公司，陕西 西安 710043；2.轨道交通工程信息化国家重点实验室(中铁一院)，陕西 西安 710043；3.西南交通大学 地球科学与环境工程学院，四川 成都 611756)

当采用最小二乘法进行既有铁路平面线形拟合时，需首先判断测点所在位置的平面线形(即线形识别)并将实测数据分组，然后依据相应拟合模型对各组实测数据进行线形拟合。然而，既有铁路平面线形的实测坐标数据不可避免地存在偶然误差或粗差，这将对线形识别产生不利影响，从而导致实测数据分组不准确，进而造成线形拟合的效果较差。鉴于以上原因，提出基于选权迭代法的既有铁路平面线形拟合方法。该方法将各分组内不属于待拟合线形内的测点视作含粗差的测点，并利用选权迭代法具备的较强抗差能力对其进行检测和剔除，最终实现无需精确分组的既有铁路平面线形拟合，获得可靠的线形拟合参数估值。

最小二乘；既有铁路；拟合；线形识别；粗差；选权迭代法

受列车重力、离心力以及其他各种因素的影响，铁路轨道的空间位置及轨道不同位置间的相对位置会发生变化，从而造成既有铁路轨道不平顺和线形的整体偏移[1-2]。轨道不平顺必将对列车运行的稳定性和舒适度产生不利影响，严重时甚至危及行车安全[2-4]，因此，需要定期对既有铁路的几何状态进行检测并对轨道进行调整以保证轨道的高平顺性。常规调整方法是以设计线形为基准进行轨道调整，但当既有铁路轨道位置发生较大的整体一致性偏移时，若仍以设计线形为基准进行轨道调整势必会增加工作量和维护成本，严重时甚至无法进行轨道调整。针对常规调整方法存在的问题，文献[5]在满足《铁路线路设计规范》的前提下，通过实测坐标构建平面及纵断面上的优化线形，并依据优化线形进行轨道调整，最终使得在轨道调整量较小的同时实现轨道的高平顺性，这对降低铁路维护成本和提高维护效率具有重要意义。线形拟合是线形优化的前提，铁路平面线形由直线、圆曲线、缓和曲线3种基本线形单元构成。由于不同线形的拟合模型不同，因此，采用最小二乘法进行线形拟合时，需首先进行线形识别并将实测数据分组[5]。因抗差能力较差，故用最小二乘法进行既有铁路平面线形拟合对实测数据分组提出了较高的精度要求。针对上述问题，陈海军[5]提出高精度的分段方法，但该方法是在假设实测坐标数据中不存在粗差的情况下提出来的，一旦数据存在较大或较多粗差，该方法便无法得到可靠的分组结果，进而导致所估线形参数不可靠。鉴于上述原因，本文提出无需对实测数据精确分组并具有较强抵抗粗差能力的既有铁路平面线形拟合方法，称之为基于选权迭代法的既有铁路平面线形拟合方法。

1 理论基础

1.1 选权迭代法

最小二乘估计是建立在观测值来源于正态分布基础上的。在观测值服从正态分布的情况下，最小二乘估计是最优线形无偏估计，具有最优统计特性[6]。然而正态分布是一种在假设或理想情况下的数据分布，大量实验证明，严格地服从正态分布的观测数据几乎没有[7-9]。统计学家研究发现，含有粗差的观测量约占总观测量的1%～10%。抗差估计正是针对最小二乘法抵抗粗差能力差这一缺陷提出来的，抗差估计对模型误差，特别是粗差具有一定的抵抗能力，所估参数能够排除或减弱受粗差的干扰[6]。抗差估计有很多种方法，但只有Huber提出的M估计有较强的实用价值，且比较容易实施[6]，选权迭代法是M估计的一种[6]。选权迭代法从第二次迭代开始利用权函数计算各观测值的权，如果权函数选择得当，且粗差是可定位的[9]，则迭代过程中含粗差的观测值的权将越来越小，直到趋近于0。迭代终止时，相应的残差将直接反映粗差的大小和位置[9]。实际作业中，外业采集的坐标数据很多，其中难免会存在一些包含粗差的数据，这些包含粗差的数据会对数据分组和线形拟合产生不良影响[10]。选权迭代法具有抵抗粗差能力强和易于编程实现的优点，可较好地顾及粗差的干扰，从而获得可靠的线形参数。

1.2 权函数及其选择

1.2.1 权函数

权函数是选权迭代法的关键，下面介绍几种常用的权函数。

1)Huber权函数

(1)

式中：pi为初始权；c为常数，一般取值为2.0；Vi为观测值改正数；σ为单位权中误差。

2)丹麦法权函数

(2)

式中：pi为初始权；c为常数，一般取值为1.5；Vi为观测值改正数；σ为单位权中误差。

3)IGGⅢ方案权函数

(3)

式中：pi为初始权；Vi为标准化残差[10]；k0通常取值为1.5～2.0；k1通常取值为3.0～8.5。

1.2.2 权函数的选择

现有的权函数有许多种，除了上文提及的3种权函数外，还有Hampel权函数、Fair权函数和Tukey权函数等。选权迭代法抗差效果的好坏很大程度上取决于所使用的权函数，权函数的良好选择取决于测量数据的误差分布情况，但误差分布难以准确获知，故目前只能在若干种有代表性的类型中去选择。马洪磊[10]根据经验和实际应用效果，认为丹麦法权函数进行粗差检验比较有效。杨元喜[11]则认为选用的权函数应包含3段：1)自然段：当观测误差很小时，观测值应该取原始权；2)可疑段：当观测误差较大，但并不显著时，观测值应降权；3)淘汰段：当观测值显著异常时，应将其淘汰，即取零权；杨元喜[11]对几种权函数进行分析，认为Huber权函数和丹麦法权函数均少淘汰段，这不利于提高权函数的抗差能力；IGGⅢ方案更适用于测量计算。由此可见，权函数的选取尚未固定，为找出适用于既有铁路平面线形拟合的权函数，对几种常用的权函数的计算结果进行比对，最终确定适用的权函数。

1.3 迭代终止条件

任何迭代计算都需要对应的终止条件，选权迭代法也不例外。相邻2次迭代的平差结果可作为判断迭代是否终止的基本信息，平差结果包括：1)待估参数平差值；2)观测值残差；3)单位权中误差等。迭代终止与否的判断可通过分析相邻两次迭代所得平差结果中某一项或某几项的差异大小来实现(如当相邻2次迭代所得平差结果中的待估参数平差值的差异很小时，便可终止迭代)。另外，相邻2次迭代过程中所得权阵的差异情况也可用来判断迭代是否终止，即当相邻2次迭代过程中所得权阵相同或差异很小时，便可终止迭代。由于迭代终止条件非本文的研究重点，故本文将沿用最常用的迭代终止判断条件，即由相邻2次迭代所得待估参数平差值的差异大小来决定是否继续迭代。

2 基于选权迭代法的既有铁路平面线形拟合模型

铁路平面线形由直线、圆曲线和缓和曲线3种基本线形单元组合而成。由于缓和曲线参数可由直线和圆曲线参数计算得到，因此，只需对直线段和圆曲线段进行线形拟合。不同线形的拟合模型不同，但选权迭代法具有较强抵抗粗差的能力，因此，该方法对实测数据分组的精度要求不高，现有实测数据分组方法便可满足要求，包括：1)基于超高的实测数据分组方法；2)基于斜率的实测数据分组方法；3)基于正矢的实测数据分组方法。为充分利用实测数据信息，建议把模糊测点(即无法确定其是否处于待拟合线形中的测点)归入待拟合线形的实测数据分组中。如图1，当拟合直线AB时，由于A和B两端都与缓和曲线相连，通过实测数据很难找到直线AB的端点，此时，只需将两端的模糊测点纳入该直线段的实测数据分组中即可。

图1 某铁路平面线形示意图Fig.1 Schematic diagram of a railway horizontal alignment

2.1 直线拟合模型

直线是组成铁路平面线形的基本线形单元之一，设直线方程为：

yi=kxi+b

(4)

式中：(xi,yi)为测点平面坐标；k和b为直线的斜率和截距。

由式(4)可得直线误差方程：

(5)

(6)

残差V可由下式计算：

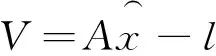
(7)

验后单位权方差为：

(8)

式中：n为观测值数；t为必要观测值数。

至此，第1次最小二乘平差计算完毕。基于选权迭代法的直线参数计算还需进行以下步骤：1)依照所选取的权函数(权函数的选择将在下文讨论)计算新权阵并平差；2)重复步骤1，直到满足迭代终止条件。

2.2 圆曲线拟合模型

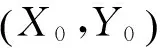
(9)

(10)

由式(9)～(10)可得圆曲线误差方程：

(11)

设观测值权阵为P(常取单位阵)，令

B=

则圆曲线参数近似值改正数的最小二乘解为：

(12)

残差V可由下式计算：

V=B·δx-l

(13)

验后单位权方差为：

(14)

式中：n为观测值数；t为必要观测值数。

至此，第1次最小二乘平差计算完毕。基于选权迭代法圆曲线参数计算还需进行以下步骤：1)依照所选取的权函数(权函数的选择将在下文讨论)计算新权阵并平差；2)重复步骤1，直到满足迭代终止条件。

利用选权迭代法计算出各直线段和圆曲线段的线形参数后，便可进行缓和曲线段线形参数的计算工作。计算方法详见文献[5]或其他相关文献。

3 对比分析

根据本文提出的方法，笔者用C#语言在.Net平台上编程实现了既有铁路平面线形的拟合计算。为选择适用的权函数并验证本文方法的正确性和可行性，进行一系列对比和分析。由于缓和曲线参数是由直线和圆曲线参数计算得到，故缓和曲线参数的精度取决于直线和圆曲线参数的精度，为缩减篇幅，只进行前、后夹直线斜率和圆曲线半径的对比。

为获得较好的拟合效果需选择良好的权函数，而抵抗粗差能力的大小是权函数好坏的直接表现，因此，可通过对比不同权函数抵抗粗差能力的大小来选择权函数。为此，在AutoCAD上模拟一段铁路轨道线形(包括前、后夹直线、缓和曲线和圆曲线)，并每隔约0.65 m读取一个轨道中线坐标组成坐标观测文件(共获得7 314个测点坐标)。分别用Huber权函数、丹麦法权函数和IGGⅢ方案权函数进行拟合计算，将计算结果与真值对比。对比情况见表1。

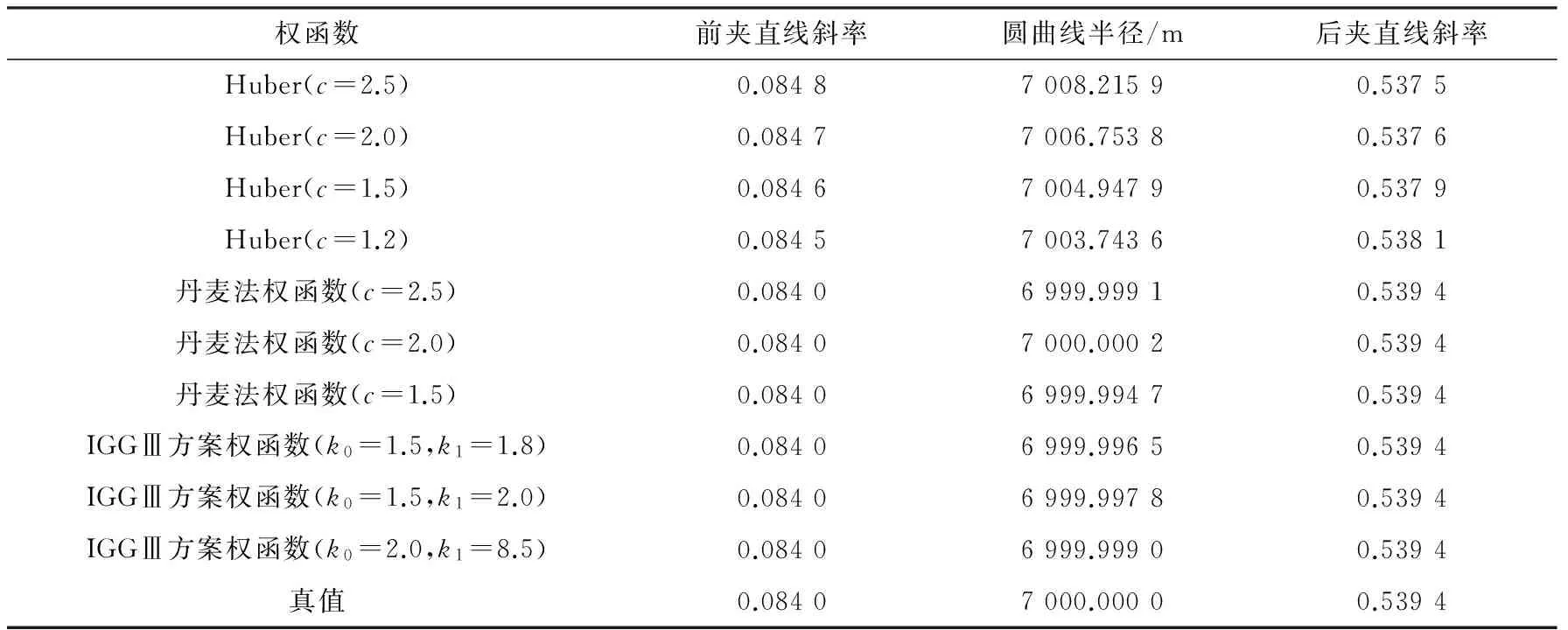
表1 不同权函数计算结果对比Table 1 Results of different weight functions

由表1可知：1)Huber权函数的计算结果与真值差异较大；2)丹麦法权函数和IGGⅢ方案权函数的计算结果均与真值差异较小。

为对比本文方法与最小二乘拟合方法，进行以下计算和对比，见表2～4。

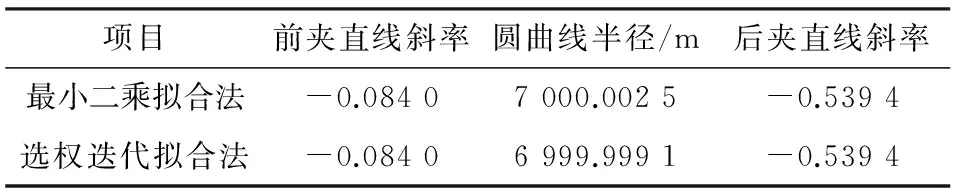
表2 最小二乘拟合法计算结果Table 2 Results of least-square fitting method

表3 观测文件中的特征点附近加入10个1 cm的粗差后2种拟合法计算结果
Table 3 Results of two fitting methods after adding 10 1 cm-gross-errors to feature points randomly in observation file

项目前夹直线斜率圆曲线半径/m后夹直线斜率最小二乘拟合法-0.08407000.0025-0.5394选权迭代拟合法-0.08406999.9991-0.5394

表4 观测文件中的特征点附近加入20个2 cm的粗差后2种拟合法计算结果
Table 4 Results of two fitting methods after adding 20 2 cm-gross-errors to feature points randomly in observation file

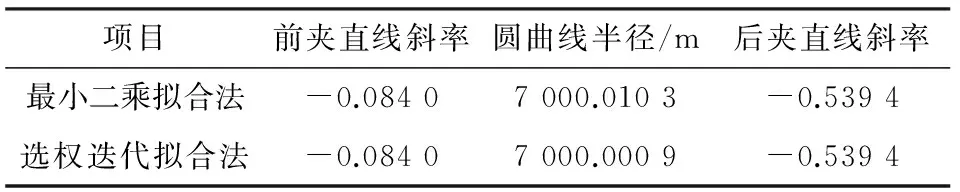
项目前夹直线斜率圆曲线半径/m后夹直线斜率最小二乘拟合法-0.08407000.0103-0.5394选权迭代拟合法-0.08407000.0009-0.5394

注：1)以上各表中选权迭代拟合法的权函数采用丹麦法权函数；2)以上各表中计算结果是在迭代终止条件为相邻2次迭代所得线形参数差值均小于0.02 mm的情况下得到的；3)斜率为无量纲

由表2和表1可知：无粗差情况下，最小二乘拟合法的计算结果较本文方法的计算结果更接近于真值。由表3和表1可知：在观测文件中的特征点附近加入10个1 cm的粗差后，本文方法的计算结果较最小二乘拟合法的计算结果更接近于真值。由表4、表3和表1可知：在观测文件中的特征点附近加入20个2 cm的粗差后，最小二乘拟合法的拟合结果与真值的偏离更加明显，本文方法的计算结果基本保持不变。

由以上对比分析可知：1)IGGⅢ方案权函数和丹麦法权函数均具有较强抵抗粗差的能力，可作为选权迭代法的权函数；2)最小二乘拟合法的拟合结果易受粗差干扰偏离真值，且粗差越多、越大，拟合结果偏离真值越明显。在粗差越多、越大情况下，本文方法的计算结果更接近于真值。

4 结论

1)基于选权迭代法的既有铁路平面线形拟合方法降低了对实测数据分组的精度要求，使用现有实测数据分组方法便可满足要求；

2)Huber权函数识别和剔除粗差的能力较弱，IGGⅢ方案权函数和丹麦法权函数具有较强的识别和剔除粗差的能力。IGGⅢ方案权函数和丹麦法权函数均可作为选权迭代法的权函数来进行既有铁路平面线形拟合；

3)基于选权迭代法的既有铁路平面线形拟合方法弥补了最小二乘拟合法抵抗粗差能力差的缺点，使得实测数据存在少量粗差的情况下仍然能够得到可靠的线形参数估值，是一种更适于实际应用的既有铁路平面线形拟合方法。

[1] 张德水.轨道不平顺的测量与数据处理[D].上海：上海交通大学，2012. ZHANG Deshui. Measurement of railway irregularities and signal processing[D].Shanghai: Shanghai Jiaotong University,2012.

[2] 李伟,蒲浩,彭先宝. 基于方向加速法的铁路既有线平面重构优化算法[J]. 铁道科学与工程学报, 2009, 6(3): 47-51. LI Wei, PU Hao, PENG Xianbao. Existing railway plane line reconstruction algorithm based on direction acceleration method[J]. Journal of Railway Science and Engineering, 2009, 6(3): 47-51.

[3] 陈峰,辜良瑶,杨岳,等.铁路既有线复测平面曲线优化方法[J]. 铁道科学与工程学报, 2012, 9(5): 90-95. CHEN Feng,GU Liangyao,YANG Yue,et al. Optimum method for horizontal curve re-surveying of the existing railway[J]. Journal of Railway Science and Engineering, 2012, 9(5): 90-95.

[4] 邓宝东,张荃.列车运行安全监控系统改进探讨[J].技术与市场，2011，18(3)：104. DENG Baodong,ZHANG Quan. Discussion of improving train coach running diagnosis system[J].Technology and Market,2011,18(3):104.

[5] 陈海军.既有线有砟轨道优化线形算法研究及其软件研制[D].成都：西南交通大学，2013. CHEN Haijun. Study of algorithm on optimization design of existing railway ballast track and software development[D].Chengdu: Southwest Jiaotong University,2013.

[6] 黄维彬.近代平差理论及其应用[M].北京：解放军出版社，1990:445-451. HUANG Weibin. Modern surveying adjustment theory and its application[M].Beijing: Chinese People’s Liberation Army Publishing House,1990:445-451.

[7] 张乐春.稳健估计在测量平差中的应用[D].北京：中国地质大学，2008. ZHANG Lechun. Application of robust estimation in the surveying adjustment[D].Beijing: China University of Geosciences,2008.

[8] 李德仁,袁修孝.误差处理与可靠性理论[M].武汉:武汉大学出版社,2007: 186-220． LI Deren,YUAN Xiuxiao. Error processing and reliability theory [M].Wuhan: Wuhan University Press,2007: 186-220．

[9] 周江文,黄幼才,杨元喜，等.抗差最小二乘法[M].武汉:华中理工大学出版社,1997: 1804-116． ZHOU Jiangwen,HUANG Youcai,YANG Yuanxi,et al. Robustified least squares approaches[M].Wuhan: Huazhong University of Science and Technology Press,1997: 1804-116．

[10] 马洪磊.既有线有砟普速铁路轨道整正算法研究[D].成都：西南交通大学，2015. MA Honglei. Algorithm research on the adjustment of ballast track of existing railway with general speed[D].Chengdu: Southwest Jiaotong University,2015.

[11] 杨元喜.等价权原理-参数平差模型的抗差最小二乘解[J].测绘通报，1994(6)：33-35. YANG Yuanxi. Least robustness square solution of equivalent weight theory-parameter adjustment model[J]. Bulletin of Surveying，1994(6)：33-35.

The linear fitting method of existing railway horizontalalignment based on iteration method with variable weights

MA Honglei1,2, LIU Chenglong3

(1.China Railway First Survey & Design Institute Group Co., Ltd, Xi’an 710043, China；2.State Key Laboratory of Rail Transit Engineering Informatization(FSDI), Xi’an 710043, China；3.Faculty of Geosciences and Environmental Engineering, Southwest Jiaotong University, Chengdu 611756, China)

When existing railway plane is fitted least square multiplication, the first step is to determine horizontal alignment of measuring points’ locations( i.e., linear identification), and cluster the measured data. Then according to the corresponding fitting model, the measured data groups are fitted linearly. However, there are unavoidable errors and gross errors in the measured coordinate data of existing railway horizontal alignment, which have adverse effects on linear identification. It will lead to inaccurate measured data grouping and cause poor quality of linear fitting. For these reasons, we propose the linear fitting method of existing railway horizontal alignment in this paper based on iteration method with variable weights. In this method, it regards the measured points beyond being fitted linearly in different groups as measured points with gross errors. It detects and eliminates points by using the robust correction ability of iteration method with variable weights. Ultimately, it can realize existing railway horizontal alignment without accurate grouping, and obtain the reliable parameters valuation of linear fitting.Key words: least square method; existing railway; fitting; linear identification; gross error; iteration method with variable weights

2015-10-10

刘成龙(1962-)，男，福建莆田人，教授，从事精密工程测量与变形监测；E-mail: lclzwy@vip.sina.com

P207

A

1672-7029(2016)12-2375-06