基于蒙特卡洛方法的燃气蒸汽式发射装置内弹道参数分析方法①
常书丽,吕 翔,王彦涛,李鹏永
(1.中国船舶重工集团713所,郑州 450015;2.西北工业大学 燃烧、热结构与内流场重点实验室,西安 710072)
基于蒙特卡洛方法的燃气蒸汽式发射装置内弹道参数分析方法①
常书丽1,吕 翔2,王彦涛1,李鹏永1
(1.中国船舶重工集团713所,郑州 450015;2.西北工业大学 燃烧、热结构与内流场重点实验室,西安 710072)
利用蒙特卡洛随机分析方法,对燃气蒸汽式发射装置内弹道参数的随机分布特性进行了研究。在大量试验数据的基础上,提出了采用统计方式对模型进行一致性检验来代替传统的模型校验方法。结果表明,所采用的内弹道计算模型在置信度γ= 0.95下是可信的。内弹道随机分析结果表明,在现有状态下,导弹出筒速度的精度范围无法满足±2 m/s(概率为0.997 4)的设计指标要求。根据参数敏感性分析结果,提出了通过控制装药出厂燃速、装药初温和冷却水温的随机分布规律来保证出筒速度满足设计要求的改进方案。
水下发射;发射动力;内弹道;蒙特卡洛法;灵敏度
0 引言
潜载导弹水下发射装置通常采用燃气蒸汽式发射动力装置。潜载导弹水下发射动力装置点火,产生高温高压气体,将导弹以一定速度弹射出发射筒。该装置工作稳定可靠,且不占用发射筒底空间,已得到了广泛应用。赵险峰、李咸海等假设发射筒内工质气体为冻结流,不考虑气体组分的变化,运用质量、能量等守恒定律以及气体状态方程、导弹运动方程等,对发射筒内做工的工质气体进行分析,建立了发射筒内弹道的理论计算模型,对导弹的运动过程进行描述[1-4];都军民等提出了采用蒙特卡洛方法对内弹道参数的分布进行分析[5];赵世平、肖虎斌等应用CFD技术对发射动力装置工作过程进行流场数值模拟[6-8];国外Edquist C T等[9-10]采用质量、能量等各种守恒定律、气体状态方程、导弹运动方程等,在发射筒内气体分别为冻结流和化学平衡气体两种情况下,建立了弹射过程筒内弹道数学模型,对筒内气体的热力过程和导弹运动规律进行了较全面的分析。
在进行型号设计时,导弹总体通常要求发射装置工作的导弹出筒速度、导弹运动加速度、发射筒内压力、发射筒内温度等参数满足特定的指标要求。内弹道预示就是采用理论分析的方式,根据特定的初始条件和设计的工作状态,对导弹筒内运动过程进行计算,获得导弹运动参数,以判定所设计的工作状态能否满足指标要求。
导弹水下发射是一个复杂的物理化学过程,内弹道理论预示与实际结果必然存在一定差异。实践表明,同一型号、同一批次发射动力装置,在相同试验条件下的内弹道参数呈随机性散布。显然,内弹道预示存在一定的预示偏差。对于预示偏差的确定,传统处理方法是将所有影响因素同时取上极限确定上偏差,将所有影响因素同时取下极限确定下偏差。所有影响因素同时走极限值,在实际发射过程中是一个小概率事件。因此,这种确定预示偏差的方法趋于保守。
本文通过收集大量的试验数据,研究内弹道影响因素的分布规律,采用蒙特卡洛的方法,对各内弹道影响因素进行大量的随机抽样,求解出内弹道参数的分布特性,以概率统计方式对内弹道参数进行分析。
1 发射装置内弹道计算模型
1.1 发射装置基本工作原理
燃气蒸汽式发射装置主要由燃气发生器、冷却器、弯管、发射筒等部分组成,如图1所示。导弹水下发射时,点火保险机构点火,燃气发生器内药柱燃烧产生高温高压燃气,燃气经过分流管的分流在冷却器内喷水管内外形成喷水压差,将冷却水经过喷水孔喷入喷水区[5]。在喷水区内冷却水与高温高压燃气发生剧烈掺混,水吸热汽化,达到降温和调能的目的。掺混后的混合气体经过动力弯管流入发射筒底,在筒底建立压力推动导弹做功,将导弹弹射出去。
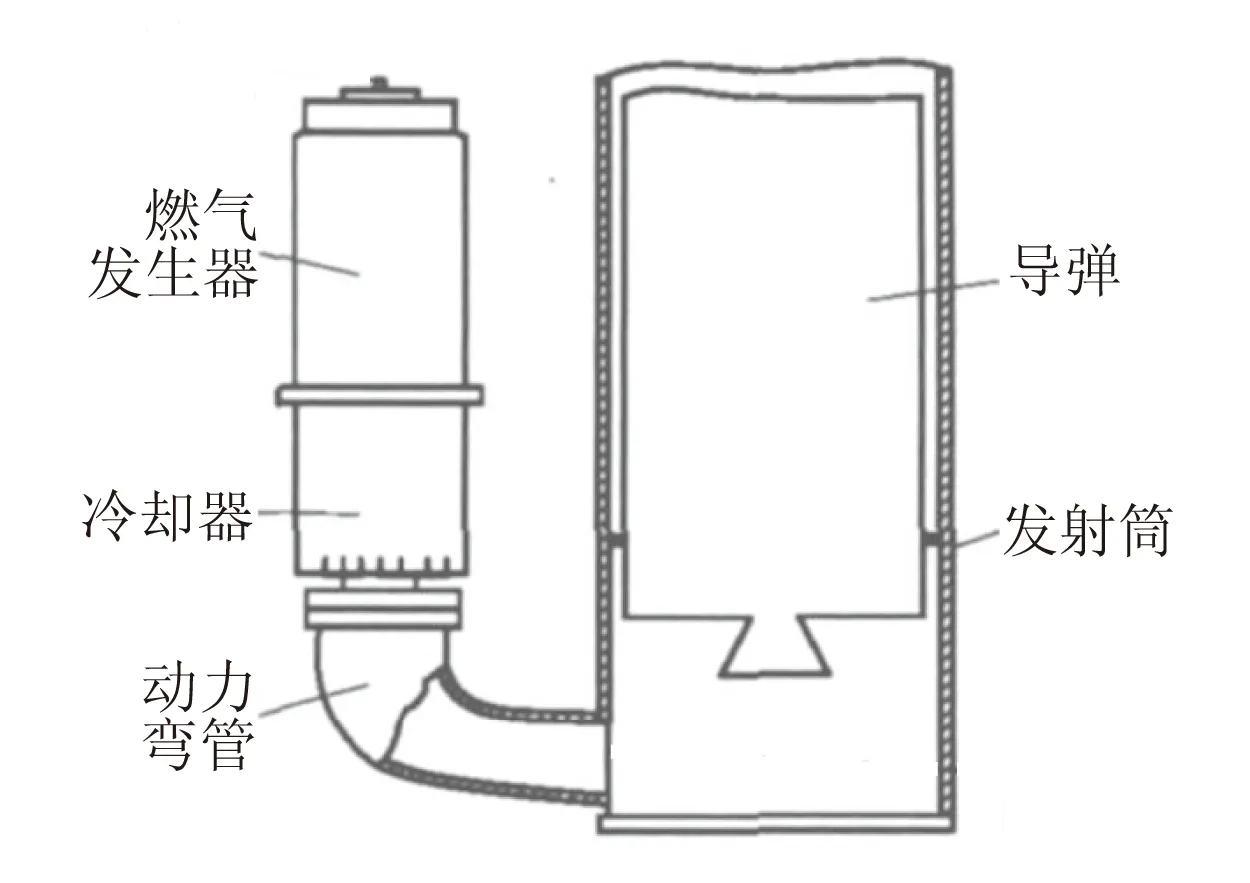
图1 燃气蒸汽式发射装置结构图Fig.1 Layout of combustion gas-steam launching system
1.2 内弹道计算模型
由于发射装置工作过程复杂,影响因素众多,在理论分析时,将发射装置工作过程进行简化,抓住关键环节,建立了发射装置工作过程的主要控制方程组。
燃气发生器内部压力计算方程为
(1)
式中pc为燃气发生器压力;ρp为药柱密度;u0为药柱出厂燃速,即温度T0、压力p0下的燃速;αT为药柱温度敏感系数;Ta为药柱初温;C*为药柱特征速度;Ab为燃面;At为喷管横截面积;ν为药柱压强指数。
通过燃气发生器喉部流出的燃气质量为
(2)
冷却器内部包含了高温高压燃气湍流流动、冷却水喷注、水与燃气掺混雾化等复杂的传热和相变等过程,具体过程已不能用控制方程描述,但通过小孔流量关系,可计算出通过冷却器喷注与燃气掺混的水量。
(3)
式中μ为流量系数;s1喷水孔横截面积;g为重力加速度;ρ为水的密度;λ为喷水压差系数。
能量守恒方程为
(4)
式中XemgCvgTvg为燃气初始能量;m1C1T1为冷却水的初始能量;mrCvrTr为筒底空气初始能量;U2为发射筒内混合气体内能。
气体状态方程为
(5)
式中pt为发射筒内压力;Tt为发射筒内温度;Rg、Rr分别为燃气和空气的气体常数;mg、mr分别为燃气和空气的质量;l0为初始容积当量长度;l为导弹运动位移;p1为水蒸气的分压。
导弹运动方程为
Ma=ptSt-F+Fx
(6)
F= Mg+Fz+f·ptSt+p0St+ρg(HSt-lSm)+
(7)
式中Fx为产气装置推力;Fz为摩擦力;f为气密环相关参数;Cx为流体阻力系数;φ为附加质量系数。
1.3 模型检验
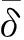
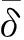
(8)
式中δδ为δ的样本偏差;tα/2(n-1)为t分布的α/2分位点。
搜集14发燃气蒸汽式发射装置大型试验数据,模型计算的导弹出筒速度误差情况见表1,其他内弹道参数计算误差统计情况见表2。

表1 内弹道参数的计算误差统计结果Table 1 The calculational error of the velocity
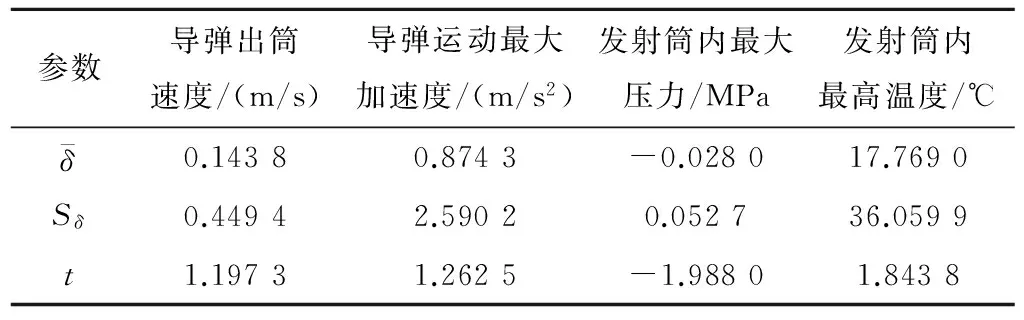
表2 内弹道参数的计算误差统计结果Table 2 The calculational error of the interior ballistics parameter
在显著水平α=0.05(置信度γ= 0.95)下,查双侧置信区间t分布表得
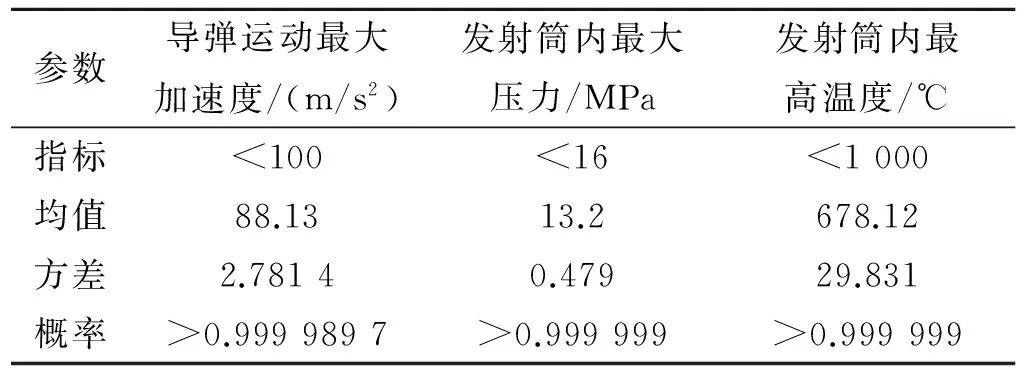
tα/2(n-1)=2.364 6
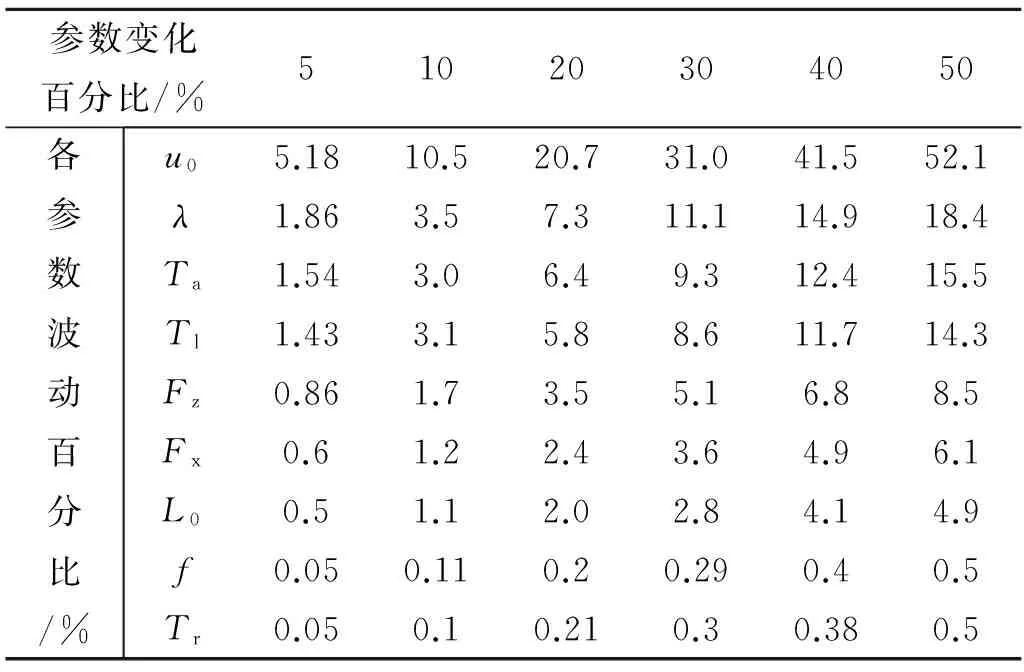
显然,对于导弹出筒速度、导弹运动最大加速度、筒内最大压力、筒内最高温度均有|t| 2.1 参数分布规律 潜载导弹水下发射过程中,影响内弹道预示的因素主要有药柱燃速、初温、喷水孔数、喷水压差系数、冷却水初温、发射深度、导弹重量、气密环摩擦系数、导弹发射摩擦力、弹底部空气初温、导弹流体阻力系数、产气装置推力等。 表3 正态分布各因素的取值范围Table 3 Value scope of the effect factors 2.2 蒙特卡洛分析方法 蒙特卡洛(Monte Carlo)方法又称为随机模拟方法(Random simulation),是一类通过随机变量的统计实验(或者随机模拟),求解数学、工程技术问题近似解的数值方法[13-14]。采用蒙特卡洛法,对燃气蒸汽式发射装置内弹道参数分析的流程图见图2。 仿真时,首先将所有影响因素在其取值范围内按照各自的分布规律,进行初始参数的随机抽样,根据燃气发生器参数抽样结果,进行燃气发生器内弹道计算,获取pc-t曲线;再根据冷却器相关参数抽样结果,结合燃气发生器pc-t进行冷却器的相关计算;最后,将所有参数汇总运用内弹道随机函数,进行发射筒内弹道计算。 图2 内弹道参数蒙特卡洛分析方法Fig.2 Method of analysis combustion gas-steam launching power equipment with Monte-Carlo 2.3 仿真次数的选择 采用蒙特卡洛法进行随机分析时,抽样数量的选择可借鉴可靠性评估的相关理论,燃气蒸汽式发射装置可靠性评估时,将系统等效成成败型数据,成败型单元在给定置信度γ下,其可靠度的置信下限RLc为 (9) 式中f=N-s;N为试验成功数;f为试验失败数。 特殊地,如果单元的可靠性试验数据中的失败次数f=0,则其可靠度置信下限为 (10) 根据搜集到的数据,燃气蒸汽式发射装置在已经进行的试验中失败次数为0,这样仿真次数的选择可借鉴f=0时的置信下限表达式,推导出仿真次数N=lg(1-γ)/lg(RLc),在置信度γ=0.95、可靠度的置信下限RLc取3σ(0.997 4)时,计算得到仿真次数N=1 151,本文取N=1 200。 3.1 仿真结果正态分布检验 对1 200组内弹道参数仿真结果进行统计,结果见表4。对内弹道参数仿真结果绘制直方图,如图3~图6所示。 由以上各参数直方图初步判断导弹出筒速度Ve、导弹运动最大加速度amax、发射筒内最大压力pt max、发射筒内最高温度Tt max4个内弹道参数均属于正态分布。在此基础上,进一步运用正态分布的拟合优度测试,对各参数进行正态分布检验,检验结果见表5。结果表明,Ve、amax、pt max、Tt max均服从正态分布。 表4 内弹道参数仿真结果均值和方差统计Table 4 Simulations of the interior ballistics parameter 图3 导弹出筒速度仿真结果直方图Fig.3 Histogram of velocity 图4 导弹运动最大加速度仿真结果直方图Fig.4 Histogram of the max acceleration 图5 发射筒内最大压力仿真结果直方图Fig.5 Histogram of the max pressure 图6 发射筒内最高温度仿真结果直方图Fig.6 Histogram of the max temperature表5 内弹道参数的正态分布检验特征值Table 5 Normal distribution test values of the interior ballistics parameters 3.2 各参数满足指标情况分析 基于以上统计的内弹道参数值的分布规律,通过计算和查正态分布表,获得导弹出筒速度偏差分别控制在±6、±5、±4、±3、±2 m/s的概率,见表6;最大加速度、压力、温度满足要求的概率见表7。 表6 导弹出筒速度满足指标的概率Table 6 Probabilities of the velocity satisfied design target 表7 加速度、压力、温度满足指标的概率Table 7 Probabilities of the max acceleration, pressure and temperature satisfied design target 依据正态分布3σ原理,导弹总体通常要求发射装置的预示结果应满足3σ(0.997 4)的概率要求。由表6和表7可看出,amax、pt max和Tt max参数满足指标的概率较高,而Ve满足±2 m/s的概率为0.876 95,达不到3σ的指标要求,因此导弹出筒速度满足指标情况成为内弹道参数满足指标的关键。 3.3 内弹道影响因素敏感性分析 为了提高导弹出筒速度的精度,需要较精确地控制对内弹道影响较大的参数。因此,需要开展内弹道影响因素的灵敏度分析[15-16]。由于在导弹总体参数已定的情况下,发射深度、导弹质量等是不可变因素,灵敏度分析时,只针对发射装置可控制的药柱燃速、药柱初温、冷却水温等参数进行。表8给出了出筒速度对各个参数的敏感性计算结果。表8中,各参数含义同表3。 表8 出筒速度对各因素变化的敏感性Table 8 Sensitivity of the velocity to effect factors 从表8可看出,对导弹出筒速度影响显著的因素主要为u0、λ、Ta、T1等。其中,u0波动对内弹道参数影响最为显著。由于λ的精度主要受机械加工精度和计量精度的影响,而目前这两者的精度已经较高。因此,需要从控制u0、Ta和T1的波动范围入手。 为了便于统一计算,可将T1=5~25 ℃的波动范围看作(15±10)℃,令σT1=10 ℃,则出筒速度的σVe值变化量可写成 (11) 式中αu0、αTa、αT1分别为出筒速度对u0、Ta、T1的敏感系数。 根据表8可知,αu0=1.04;αTa=0.31;αT1=0.29。 为了使导弹出筒速度预示值不超出(45±2)m/s的概率满足3σ的指标要求,即 ≥0.997 4 (12) 则据式(12)计算得到出筒速度的σVe值,必须满足σVe≤0.55。因此,通过控制各个影响因素,使σVe的变化量满足ΔσVe≥1.217 3-0.55=0.667 3时,方可保证出筒速度满足3σ要求。 通过仔细分析各个参数精度的可控范围,取Δσu0=50%、ΔσTa=33%、ΔσT1=50%,即将σu0由2 mm/s控制在1 mm/s以内,将药柱初温的σTa由3 ℃控制在2 ℃,同时将冷却水温的σT1由10 ℃控制在5 ℃以内,计算得ΔσVe=0.767 3,导弹出筒速度满足±2 m/s的概率为0.998 576,满足3σ的概率要求。 (1)针对建立的燃气蒸汽式发射装置内弹道计算模型,在大量试验数据的基础上,利用统计学方法对模型进行了一致性检验。结果表明,模型计算结果与试验实测结果在置信度γ=0.95下是可信的。 (2)基于蒙特卡洛方法,建立了燃气蒸汽式发射装置内弹道随机分析方法。内弹道随机分析结果表明,在现有设计方案下,导弹在发射筒内最大加速度、发射筒内最大压力和最高温度均满足设计指标要求,而导弹出筒速度无法满足要求。 (3)敏感性分析结果表明,对导弹出筒速度影响显著的因素主要为装药出厂燃速、喷水压差系数、药柱初温和冷却水温等。根据敏感性分析结果,提出了通过控制装药出厂燃速、药柱初温和冷却水温,来提高内弹道预示精度的方法。 [1] 李咸海, 王俊杰. 潜地导弹发射动力系统[M]. 哈尔滨工程大学出版社, 2000. [2] 赵险峰, 王俊杰. 潜地弹道导弹发射系统内弹道学[M]. 哈尔滨工程大学出版社, 2000. [3] 赵世平. 潜地弹道导弹变深度发射动力系统有用能调节机理研究[D]. 西北工业大学, 2007. [4] 惠卫华, 鲍福廷, 刘旸. 考虑低燃温燃气发生器试验的弹射器内弹道性能预示[J]. 固体火箭技术, 2013, 36(6): 715-719. [5] 都军民, 汪太琨. 利用蒙特卡洛方法对导弹筒内弹道参数的分布进行分析[J]. 弹舰与制导学报, 2002, 22(4): 45-47. [6] 肖虎斌, 赵世平. 燃气蒸汽式发射动力装置复杂内流场数值模拟[J]. 固体火箭技术, 2009, 32(4): 392-395. [7] 沈国. 蒸汽弹射系统内弹道数值模拟与参数设计[D]. 南京: 南京理工大学, 2011. [8] 吕翔, 李江, 陈剑, 等. 变深度水下发射系统内弹道实验研究[J]. 固体火箭技术, 2012, 35(1): 24-28. [9] Edquist C T. Prediction of the launch pulse for gas generator launched missiles[R]. AIAA 88-3290. [10] Edquist C T, Romine G L. Canister gas dynamics of gas generator launched missiles[R]. AIAA 80-1186. [11] 苏岩. 多元分布拟合优度检验研究进展[D]. 保定学院学报, 2011, 25(3): 1-7. [12] 董聪, 戎海武, 杨庆雄. 先进拟合优度检验方法及应用[J].强度与环境, 1994, 22(1): 23-31. [13] 房雷, 张万里. 基于蒙特卡洛的发动机推力线横移数值仿真[J]. 弹舰与制导学报, 2013, 34(3): 109-111. [14] 王永杰. 基于蒙特卡洛方法求取故障导弹飞行落点概率方法研究[J]. 系统工程与电子技术, 2008, 30(4): 682-685. [15] 田四朋, 唐国金, 雷勇军, 等. 固体火箭发动力随机药柱结构分析参数的灵敏度研究[J]. 固体火箭技术, 2008, 31(1): 28-32. [16] 邹汝平, 李晓斌, 张为华. 固体发动机内弹道计算不确定性研究[J]. 固体火箭技术, 2009, 32(1): 33-37, 57. (编辑:崔贤彬) Interior ballistics parameters analysis about combustion gas-steam launching equipment with Monte-Carlo method CHANG Shu-li1,LV Xiang2, WANG Yan-tao1,LI Peng-yong1 (1.No.713 Institute,China Shipbuilding Industry Corporation,Zhengzhou 450015,China;2.Science and Technology on Combustion, Internal Flow and Thermal-structure Laboratory,Northwestern Polytechnical Univ., Xi'an 710072,China) The stochastic distribution of the interior ballistics parameters proposed of the combustion gas-steam launching equipment was studied with Monte-Carlo method. The statistical method was to test the interior ballistics trajectory mode instead of the traditional tect method based on lots of experiment data. The results show that the interior ballistics trajectory mode is believable onγ=0.95. Random analysis shows that the velocity precision can't satisfy the target about ±2m/s (probability was 0.997 4) at present condition. The impoved scheme of ensuring the velocity precision satisfy the target through controlling the stochastic distribution of the burning velocity of the grain, the initial temperature of the grain and the temperature of cooling water was proposed on the basis of the parameters sensitivity analysis. under water launch;launch power;interior ballistics;Monte Carlo method;sensitivity 2015-07-15; 2015-10-21。 常书丽(1983—),女,工程师,研究方向为潜载导弹水下发射技术。E-mail:csl831024@163.com V438 A 1006-2793(2016)06-0857-06 10.7673/j.issn.1006-2793.2016.06.0212 发射动力装置内弹道随机分析方法
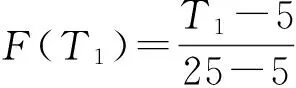
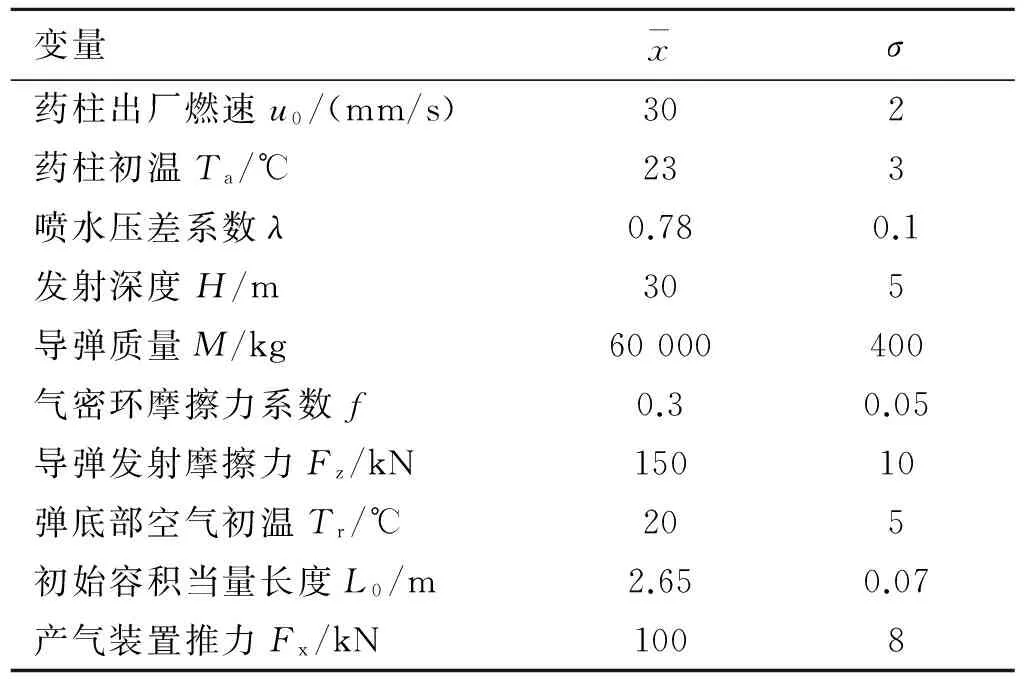
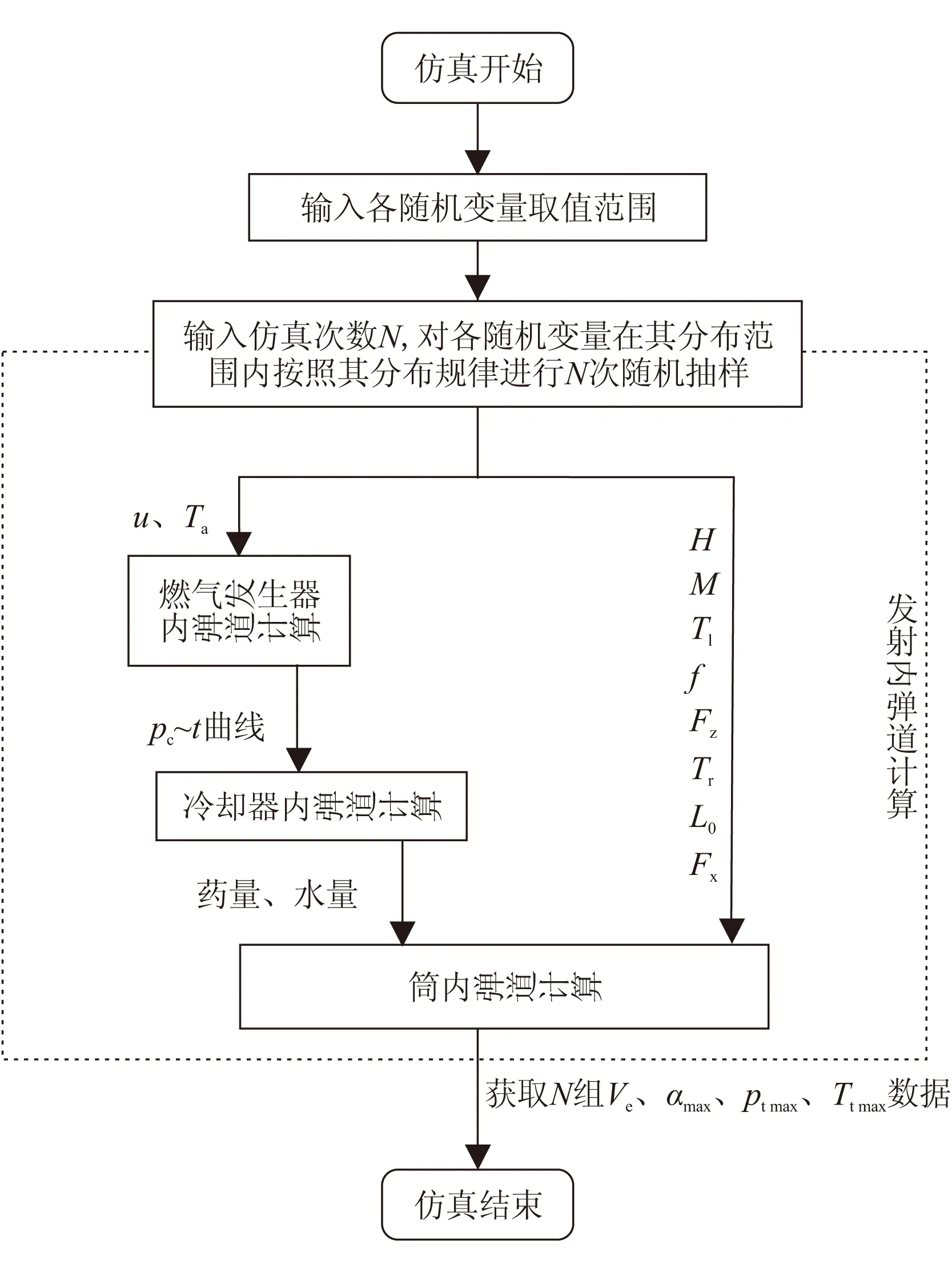
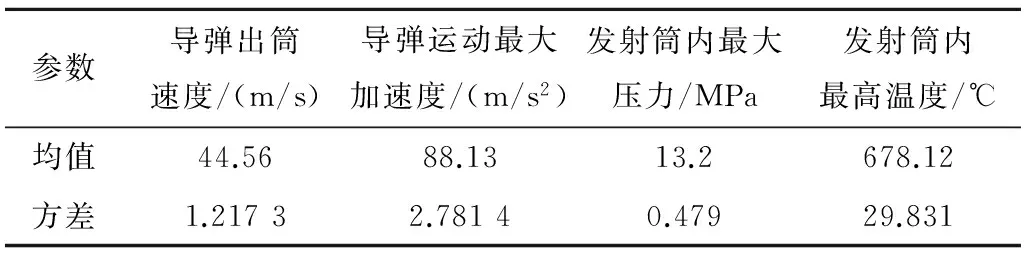
3 结果分析
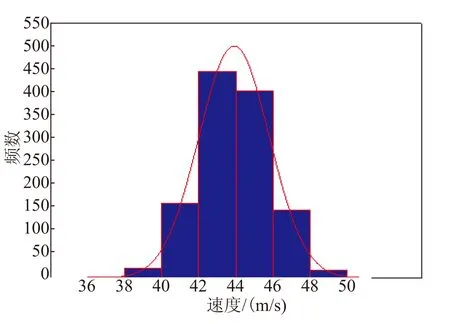
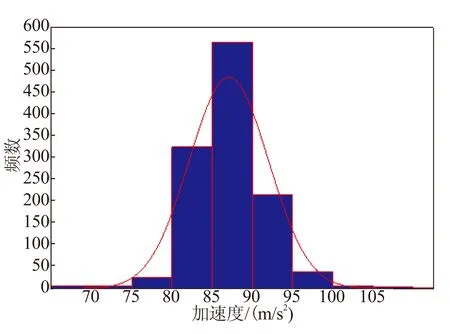
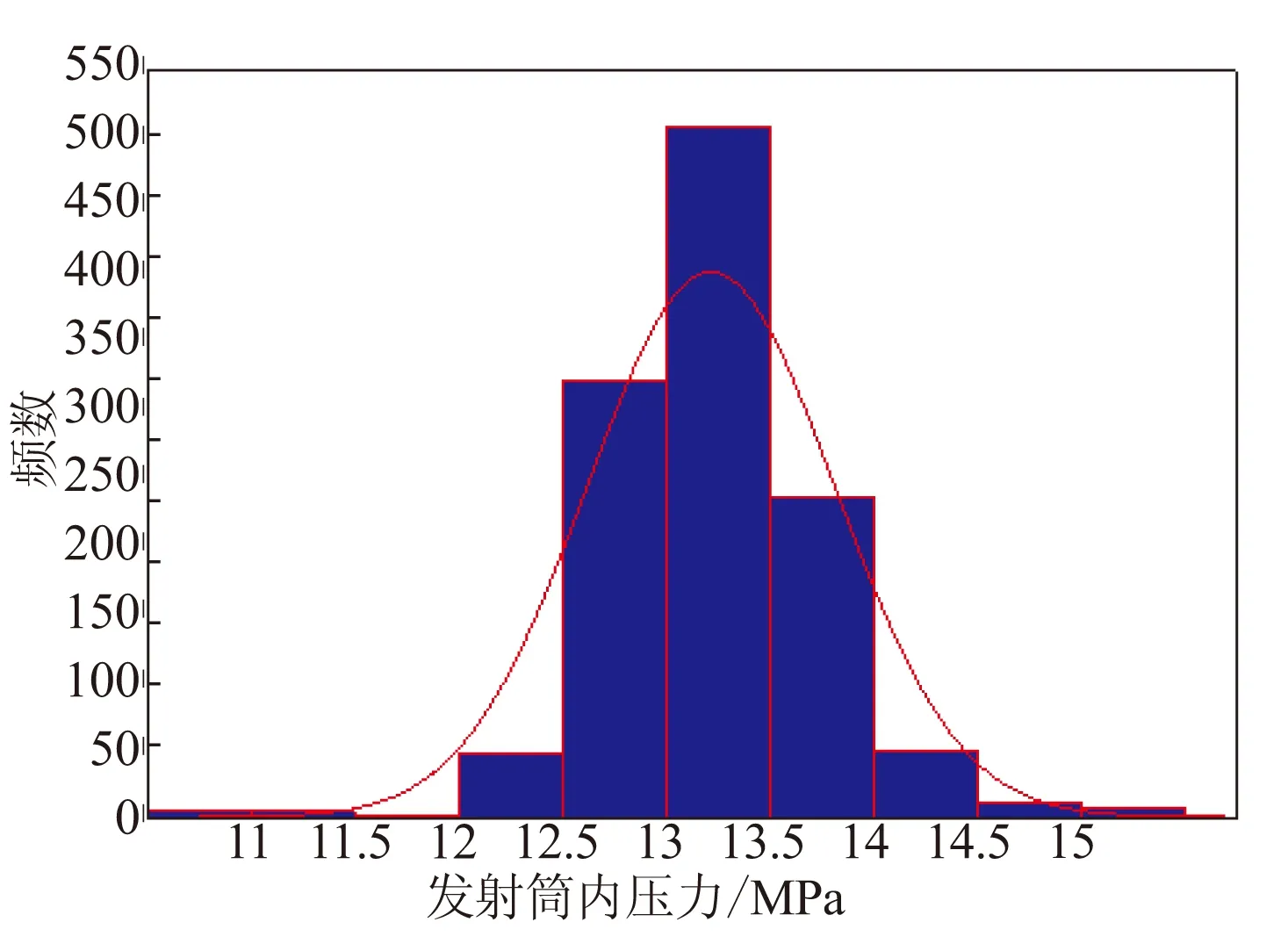
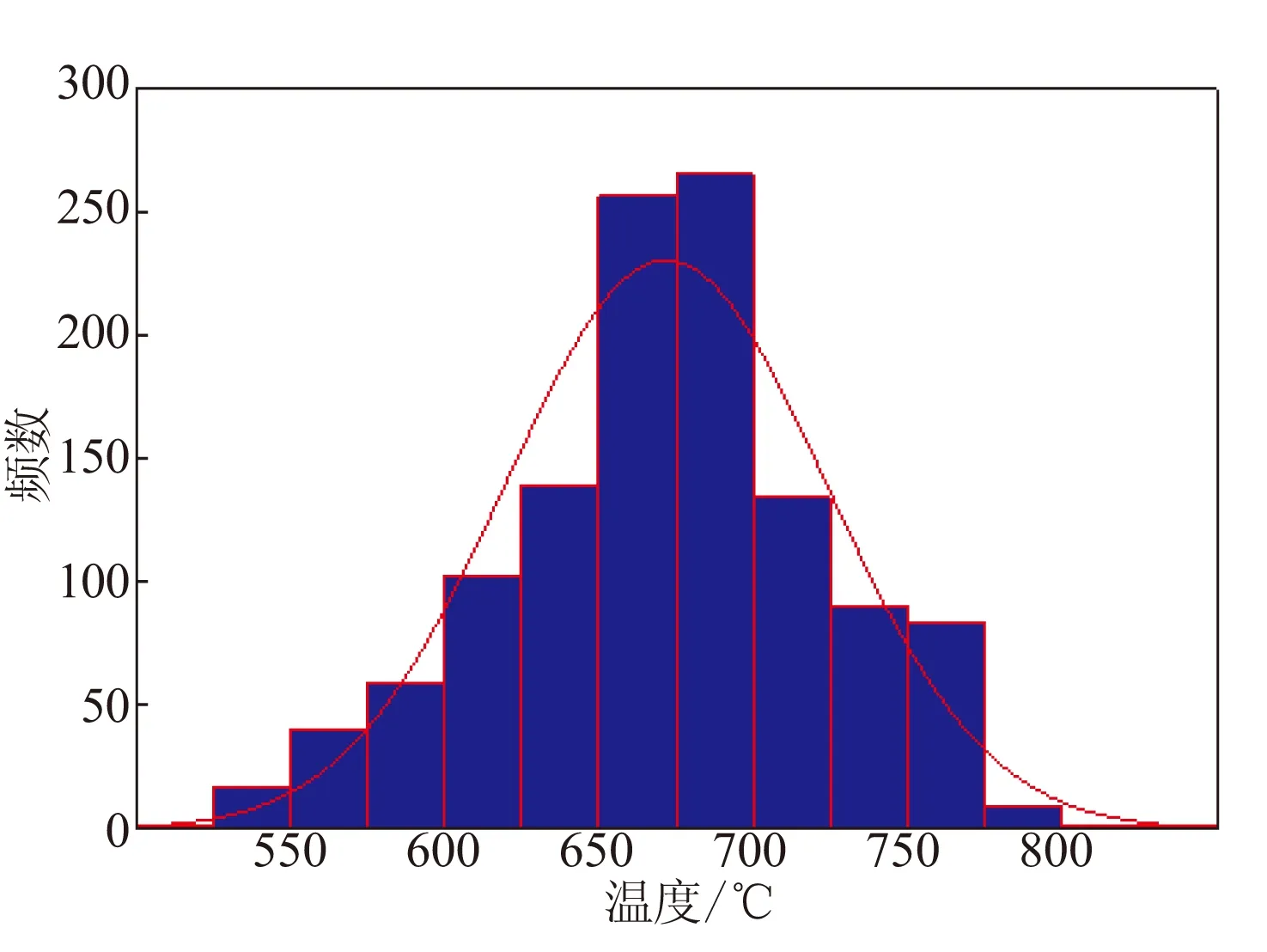

4 结论

