“喇叭花”函数赏析
2017-01-04 12:27张亚东
数学通报 2017年4期
张亚东
(上海市大同中学 200011)
1 问题提出 石破天惊”
最近高三复习调研出了这样一个填空题难倒了不少学生:


2 问题解决 “水落石出”
2.1 轨迹探究
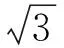
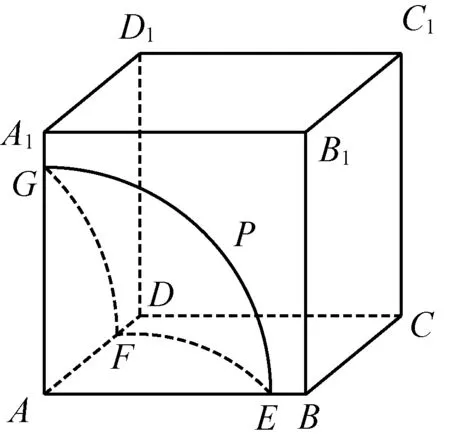
图1
我们知道用平面去截球面得到的截面图形一定是圆,圆的大小取决于球心到平面的距离.

图2

图3
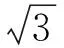

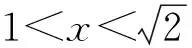
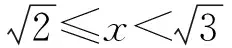
2.2 问题解决
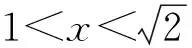
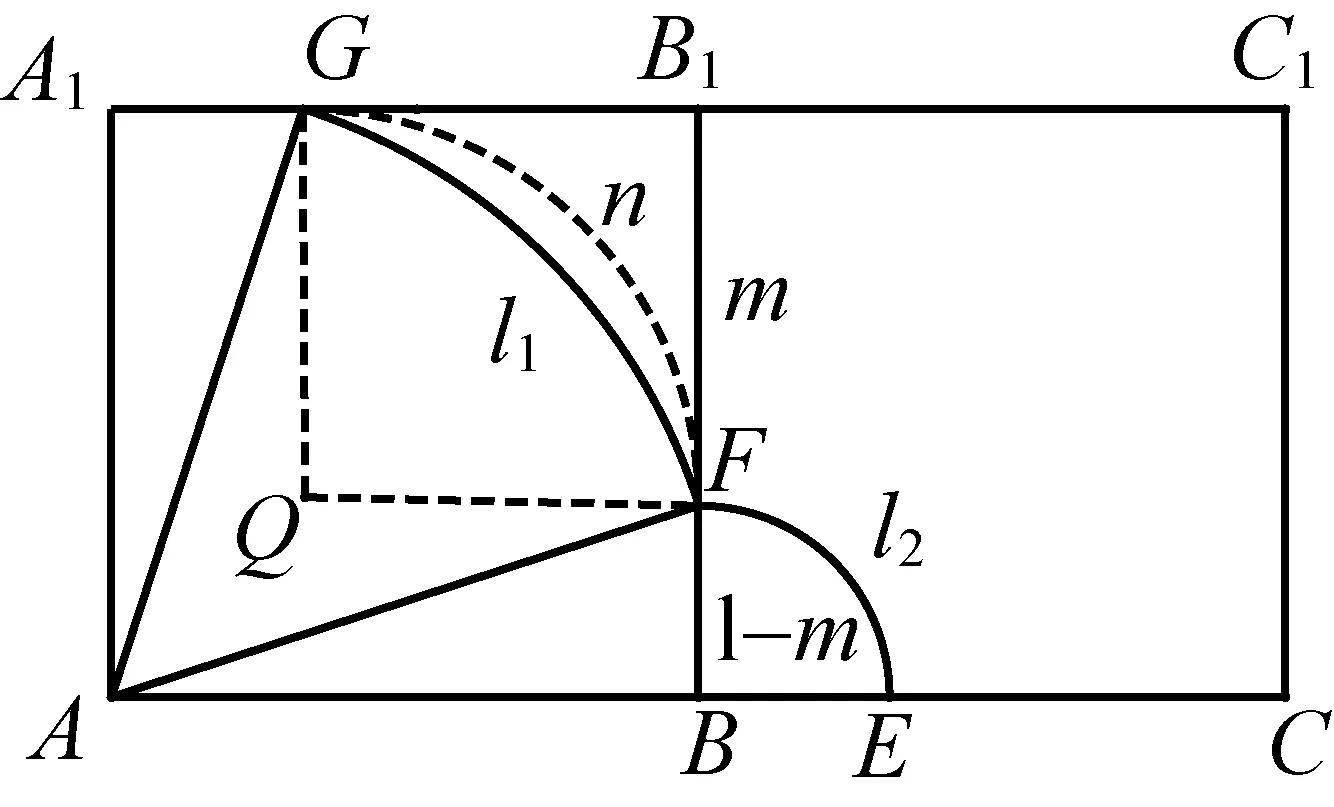
图4
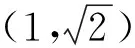
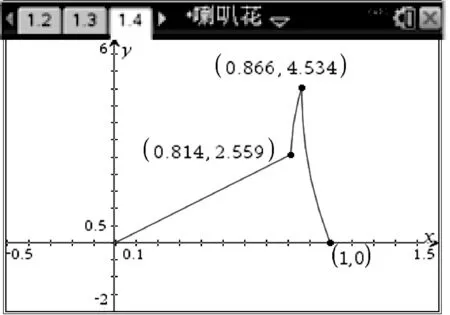
2.3 图像探究
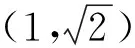
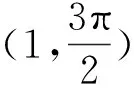
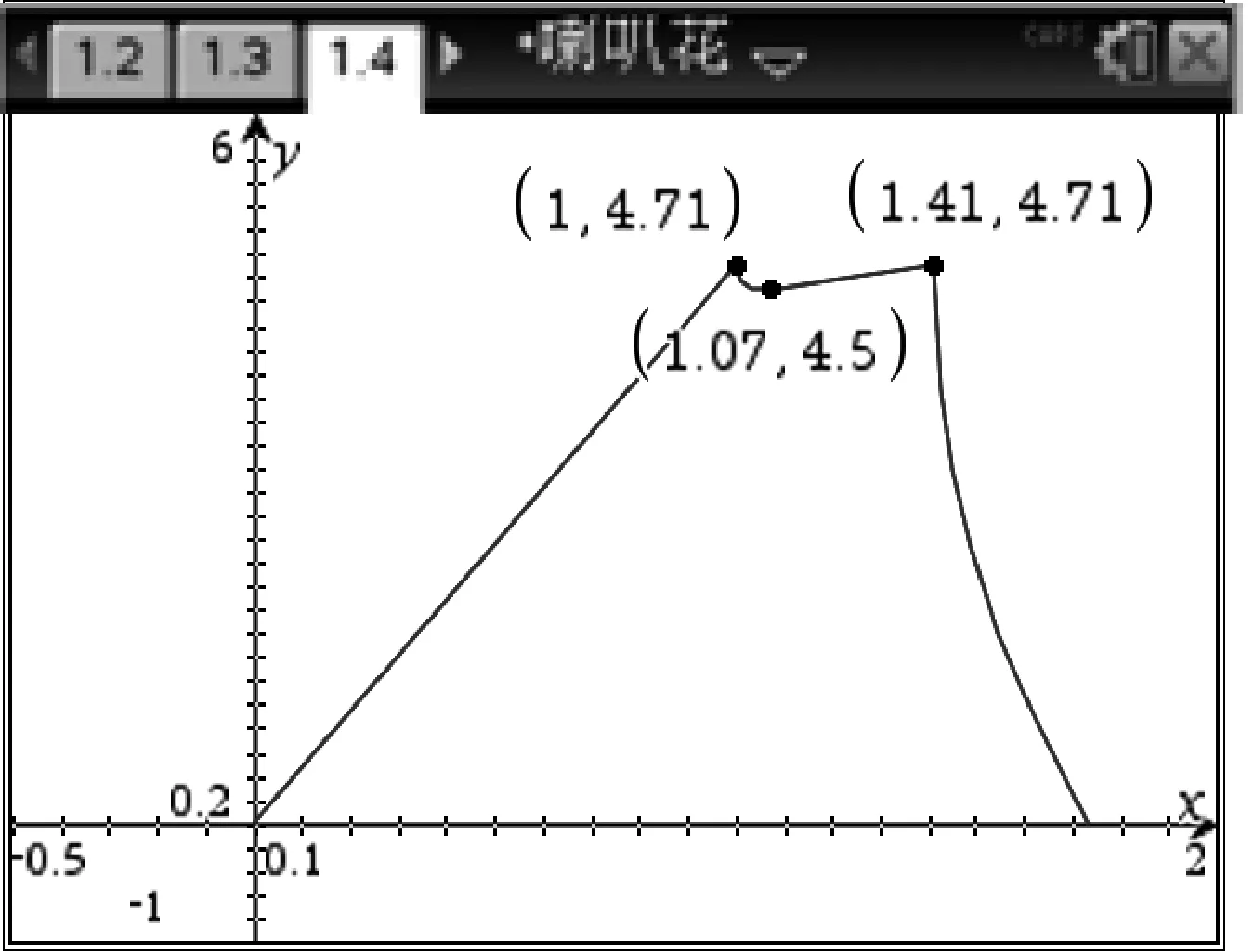
图5
3 问题生成 “再起波澜”
意犹未尽,学生提出了新的问题:“喇叭花”函数在其它正多面体中情况如何?利用类似的研究方法同样加以解决.
3.1 在正四面体中生长的“喇叭花”
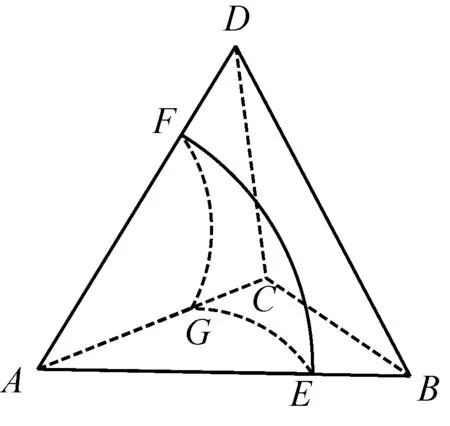
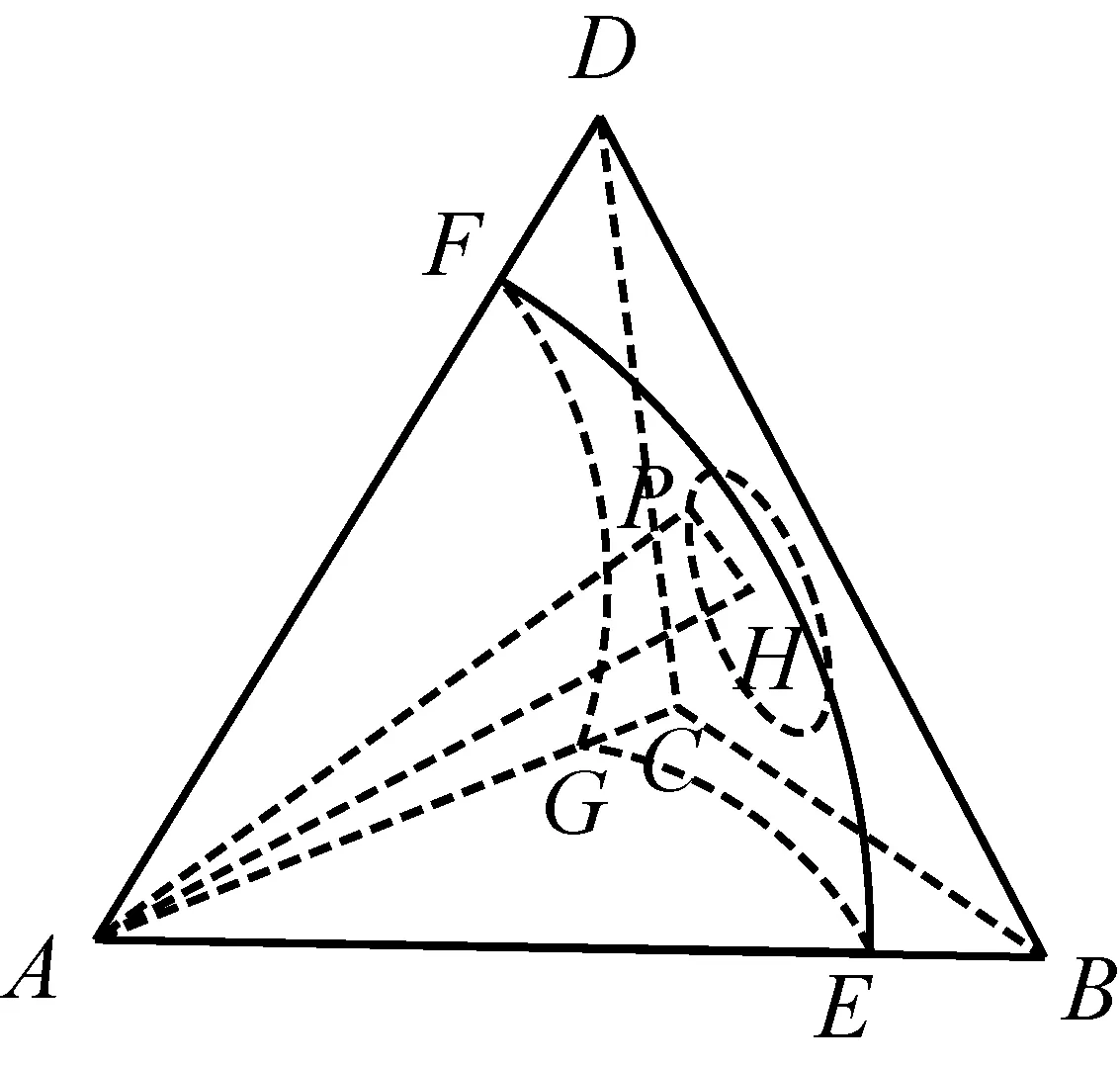
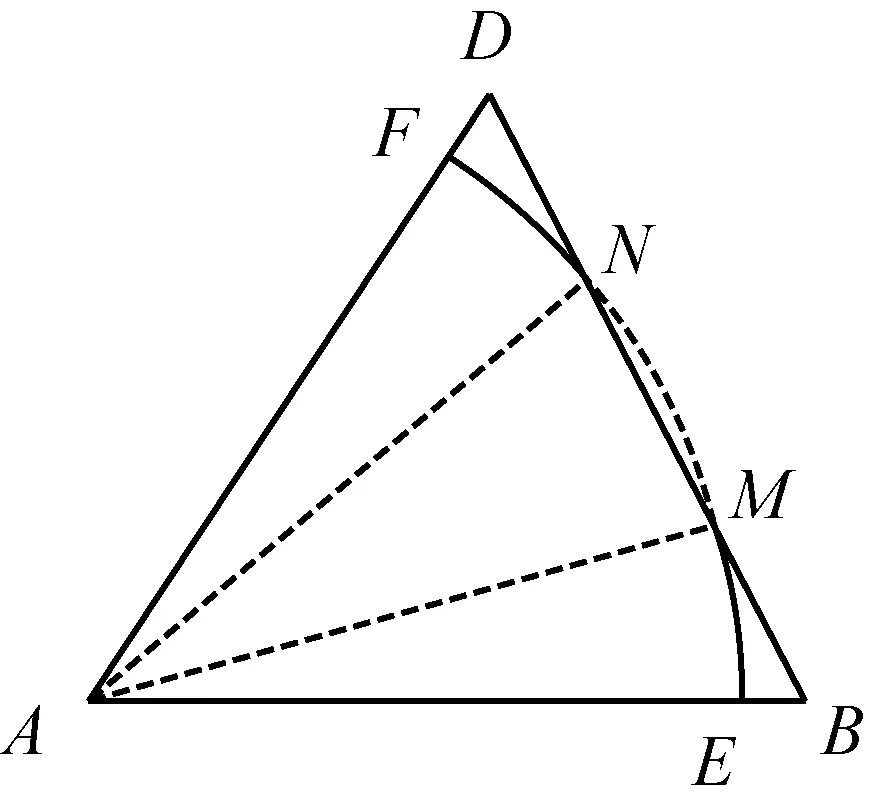
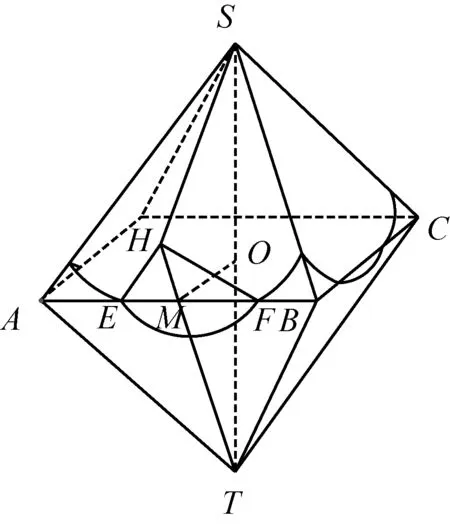
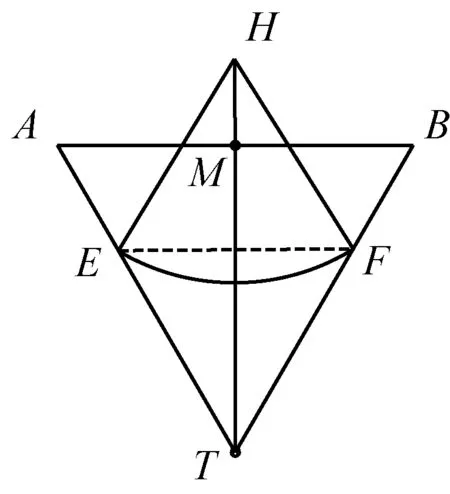
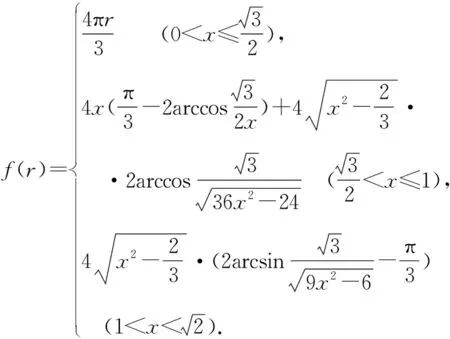
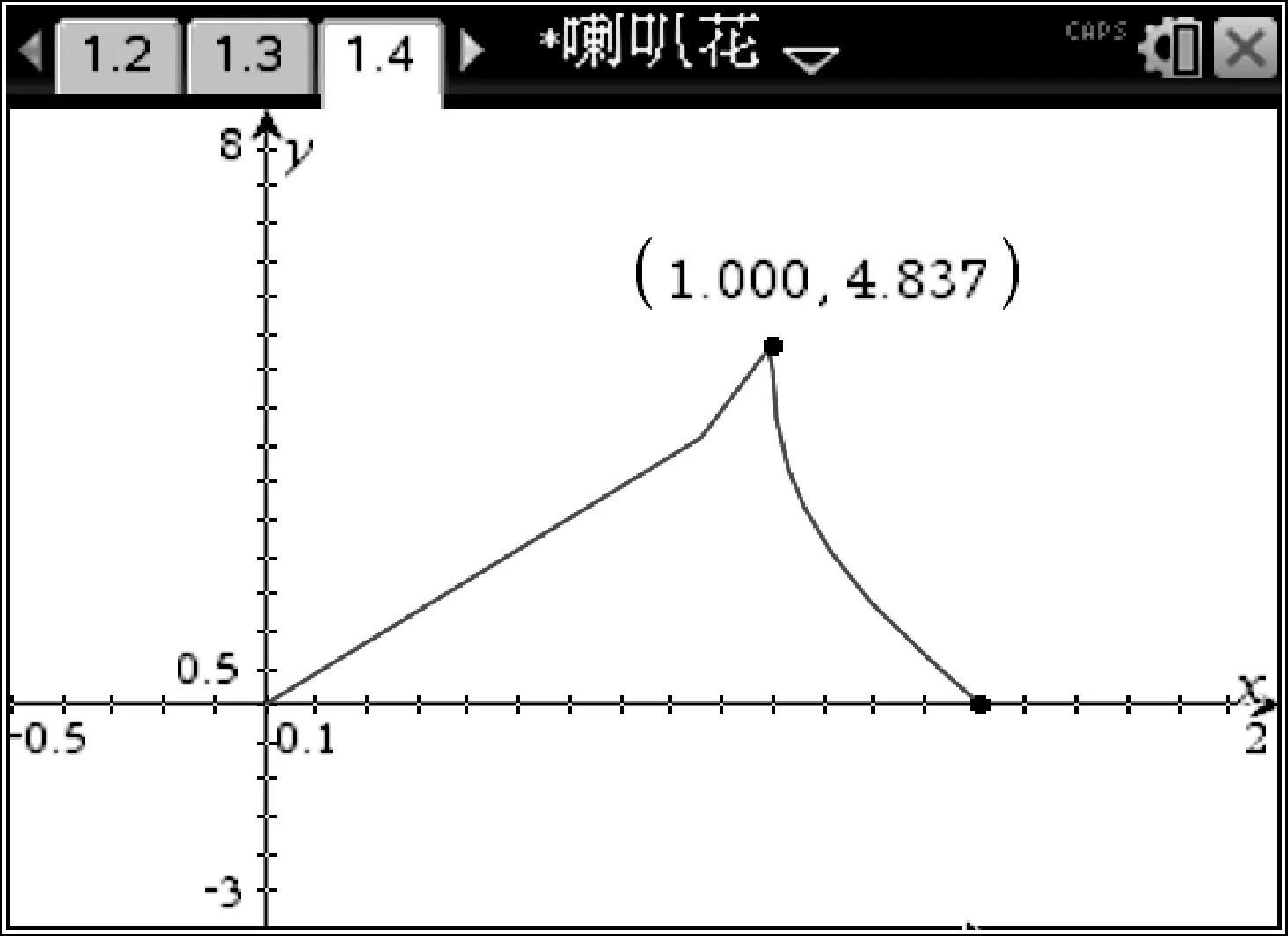
问题2:动点P在棱长为1的正四面体A-BCD表面上运动,且|PA|=x(0 随着半径x从0到1的变化,动点P的轨迹形状不尽相同,分以下三种情形: 图6 图7 图8 图9 图10 图11 点P在面TAB上的轨迹图形是什么样呢?为此取AB中点M,过点S作SH⊥TM,垂足为H,易证SH⊥面TAB,所以点P在面TAB上的轨迹是以H点为圆心,HE为半径的一段圆弧. 图12 当x=1时,TE正好与轨迹圆弧相切(图15). 图13 图14 图15 图16 作出函数图像(图17),在正八面体中,关于x的方程f(x)=m解的个数可能为0,1,2. 图17 在正八面体中的“喇叭花”函数图像与正四面体中的图像形状相似,先直线上升,然后盛开,接下来开始凋谢,所不同的是它在生长过程中始终 没有出现“花蕊”,盛开得更慢一些,开得最盛时的 花朵要大一些,花期也更长一些. 运用类似的方法可以继续研究“喇叭花”在正十二面体和正二十面体中盛开的情况,可以想象它们将会更为绚丽夺目,五彩缤纷.其实,“喇叭花”函数不仅仅可以在正多面体中盛开,对于任何多面体也存在类似的问题. 通过对“喇叭花”函数的研究,可以发挥学生的空间想象力,在问题解决过程中体悟分类讨论、数形结合的思想,学会把一个“可以想象却难以言传”的数学问题表达清楚,学会运用TI图形计算器作出函数图像,研究函数性质,探究数学问题解决途径和方法.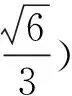


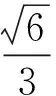


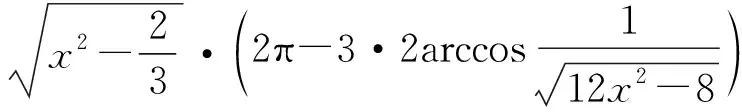

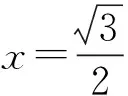
3.2 正八面体中生长的“喇叭花”
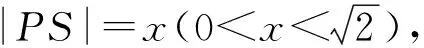
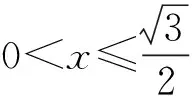
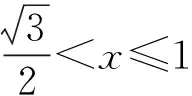



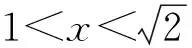
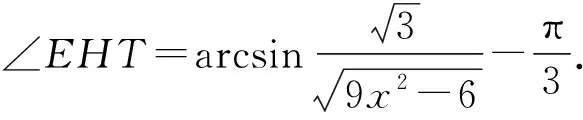
猜你喜欢
陶瓷学报(2021年3期)2021-07-22
新世纪智能(数学备考)(2019年9期)2019-10-16
小学生作文(低年级适用)(2019年4期)2019-04-29
小学生作文(低年级适用)(2019年3期)2019-04-04
阅读与作文(小学高年级版)(2017年1期)2017-04-01
物理学进展(2017年1期)2017-02-23
小主人报(2015年24期)2015-09-23
大学化学(2015年5期)2015-09-18
中学数学研究(2008年9期)2008-12-09
中学数学杂志(高中版)(2008年1期)2008-02-23

