近似邻近点算法收敛性的一个注记

李伟佳,张万里,林安

(重庆师范大学数学科学学院,重庆 401331)

近似邻近点算法收敛性的一个注记

李伟佳,张万里,林安

(重庆师范大学数学科学学院,重庆 401331)

近似邻近点算法在最优化理论与方法研究中具有重要作用.在不同误差准则下,近似邻近点算法具有不同的收敛性.利用极大单调算子等工具给出了一个具体的例子,解释了在一些误差准则下近似邻近点算法的收敛性.

近似邻近点算法;极大单调算子;误差准则

1 引言及预备知识

1970年,Martinet在文献[1]中首次提出了邻近点算法.1976年,Rockafellar在文献[2]中运用邻近点算法求解极大单调算子的零点.在实希尔伯特空间H中,极大单调算子T为H⇒H的集值映射.Rockafellar将集值映射方程的解作为新的迭代点,其中由于 Minty在文献[3]中证明了该方程解的唯一性,所以其中Pk=I+ckT-1,I为H上的恒等映射.Rockafellar在文献[2]中进一步提出了近似邻近点算法其误差准则为以下两种：

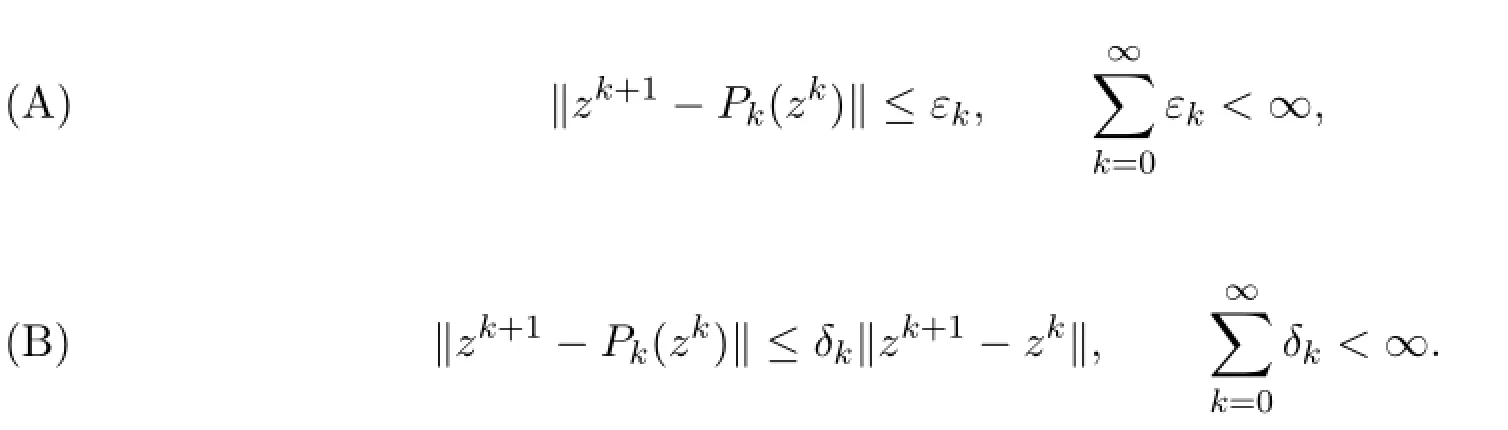
准则(A)保证了邻近点算法的收敛性.在该准则下,Rockafellar将的解作为新的迭代点.进一步,文献[4-6]推广了近似邻近点算法,研究了相应算法的收敛性.本文主要通过具体例子解释了将收敛准则(A)削弱为

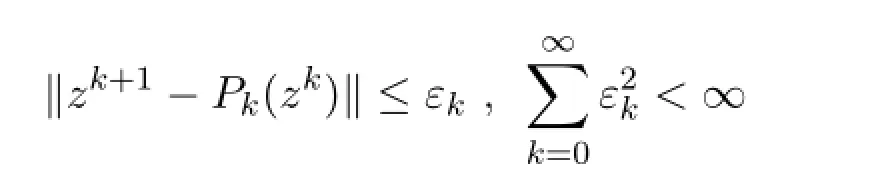
的情况下,近似邻近点算法不必收敛.下面给出本文将用到的一些基本概念：

定义 1.1[2]设H为实希尔伯特空间,其内积记为〈·,·〉.称集值映射T：HH为单调算子.如果对于任意的z,z′∈H和任意的w∈T(z),w′∈T(z′)均有〈z-z′,w-w′〉≥0.

定义 1.2[2]设H为实希尔伯特空间,其内积记为〈·,·〉.称集值映射T：HH为极大单调算子.如果T为单调算子且T的图像

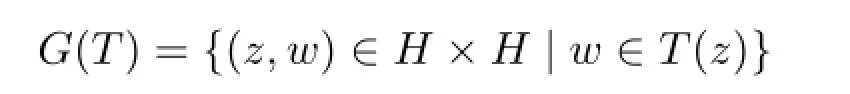
不真包含于任何其他单调算子T′：HH的图像.

2 近似邻近点算法收敛性的注记

为了讨论近似邻近点算法的收敛性,我们给出下面的一些引理.

引理2.1定义集值映射T：

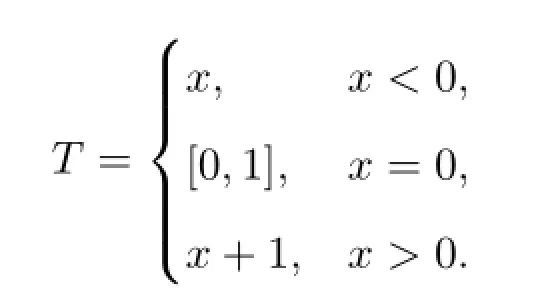
则T为极大单调算子.

引理2.2令

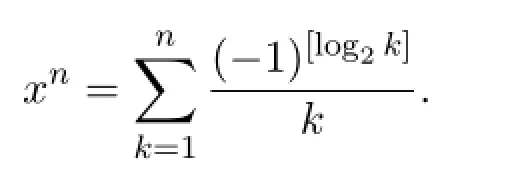
则{xn}为有界数列且满足xn∈[0,1].

定理2.1在准则

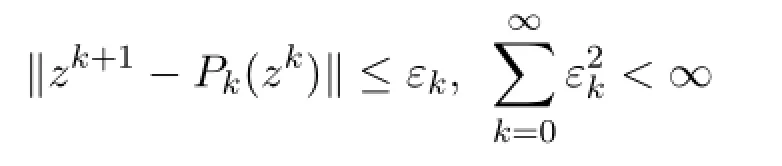
下,近似邻近点算法不必收敛.

例2.1令

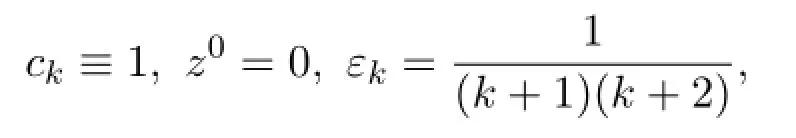
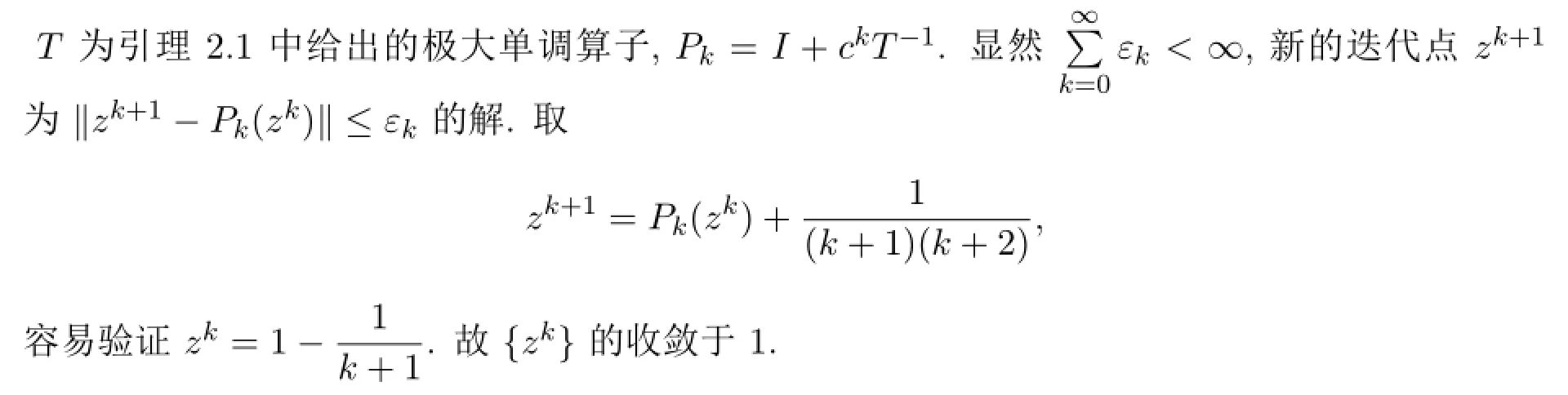
[1]Martinet B.Régularisation d′inéquations variationnelles par approximations successives[J].Rev.Francaise Informat.Recherche Opérationnelle,1970,4：154-158.

[2]Rockafellar R T.Monotone operators and the proximal point algorithm[J].SIAM Journal on Control and Optimization,1976,14：877-898.

[3]Minty G J.Monotone(nonlinear)operators in Hilbert space[J].Duke Mathematical Journal,1962,29：341-346.

[4]Chen Zhe,Zhao Kequan.A proximal-type method for convex vector optimization problem in Banach spaces[J].Numerical Functional Analysis and Optimization,2009,30：70-81.

[5]Chen Zhe,Huang Haiqiao,Zhao Kequan.Approximate generalized proximal-type method for convex vector optimization problem in Banach spaces[J].Computers and Mathematics with Applications,2009,57：1196-1203.

[6]Chen Zhe,Huang Haiqiao,Zhao Kequan.Proximal augmented Lagrangian and approximate optimal solutions in nonlinear programming[J].Journal of Applied Mathematics and Informatics,2009,27：149-159.

A note for the convergence of approximate proximal point algorithm

Li Weijia,Zhang Wanlin,Lin An
(College of Mathematics Science,Chongqing Normal University,Chongqing 401331,China)

Approximate proximal point algorithm has been playing an important role in optimization theory and methods.Under various approximate calculation,approximate proximal point algorithm has different convergence.In this paper,by means of some tools including as maximal monotone operator etc.,a concrete example is presented to illustrate the convergence of approximate proximal point algorithm with some approximate calculations.

approximate proximal point algorithm,maximal monotone operator,approximate calculation

O221.2

A

1008-5513(2016)06-0624-06

10.3969/j.issn.1008-5513.2016.06.008

2015-03-19.

国家自然科学基金(11301574);第二批重庆市高等学校青年骨干教师资助计划;重庆市研究生科研创新项目(CYS15154).

李伟佳(1990-),硕士生.研究方向：最优化理论与方法.

2010 MSC:90C30,90C48