参数识别问题混合有限元解的最大模误差估计

鲁祖亮 曹龙舟李林

(1.重庆三峡学院非线性科学与系统重点实验室,重庆 万州 404000; 2.天津财经大学数学与经济研究中心,天津 东城区 300222)

参数识别问题混合有限元解的最大模误差估计

鲁祖亮1,2, 曹龙舟1,李林1

(1.重庆三峡学院非线性科学与系统重点实验室,重庆 万州 404000; 2.天津财经大学数学与经济研究中心,天津 东城区 300222)

研究了参数识别问题混合有限元解的最大模误差估计.利用 1阶 Raviart-Thomas混合有限元离散状态和对偶状态变量,利用分片线性函数逼近控制变量,获得了状态变量和控制变量的最大模误差估计,这里控制变量的收敛阶是h2,状态变量的收敛阶是最后利用数值算例验证了理论结果.

参数识别问题;混合有限元方法;最大模误差估计

1 引言

参数识别问题的数值模拟是科学和工程计算中的一个重要研究领域,在材料力学、工程力学、工程设计等方面都有广泛应用.例如,1984年,Ewing教授总结了油藏模拟问题中的参数识别问题;1986年,Yeh教授系统研究了地下水水文问题的参数识别问题;最近,各种参数识别问题已经科学计算中大量出现[1-3],因此研究这类问题的数值计算方法就显得很重要.但是许多参数识别问题计算规模巨大,对求解速度及精度要求很高,所以提高这类最优控制问题的计算效率是急需解决的重要问题.要提高求解这类问题的计算效率,就需要借助一些先进的数学工具和计算方法.

混合有限元方法是在有限元的基础上发展起来的一个分支,已成为偏微分方程数值求解的一种重要方法.虽然由混合有限元方法所生成的代数问题比标准Galerkin方法对应的代数问题要庞大得多,但是由于这种方法对某些问题的特殊优越性,它仍然被广泛的应用于工程数值模拟和计算数学领域.

2 混合有限元方法

3 最大模误差估计

这一节,考虑参数识别问题混合有限元解的L∞先验误差估计.利用文献[8]的引理2.1,能获得如下的结论.

引理3.1令和如果τ∈Wh满足：

引理3.2假设和分别是问题(32)-问题(35)和问题(36)-问题(39)的解.如果中间误差满足：

引理 3.3设u∗是问题 (19)-问题 (23)的解,是问题 (27)-问题 (31)的解.假设u∗-y∗z∗∈H2(Ω).这时有

接下来,将获得控制变量和状态变量的最大模误差估计.首先引入一个加权的L2范数,这个范数将在获得最大模估计的过程中发挥很大的作用.令定义如下的权函数

对于任意的r∈R,定义一个r加权范数如下

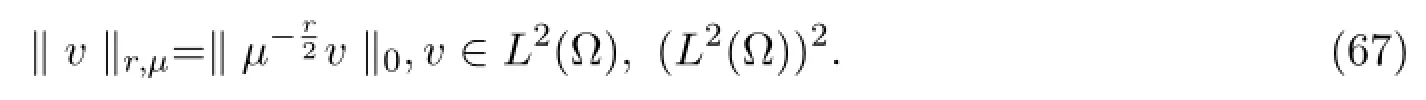
利用文献[12]中的引理3.1,得到如下结果：

引理 3.4令µ在(66)中定义,如果v∈(L2(Ω))2,这时

引理 3.5如果v∈(L∞(Ω))2,这时

进一步,引入一个加权L2范数与L∞范数的关系和一些超逼近结果[13]：

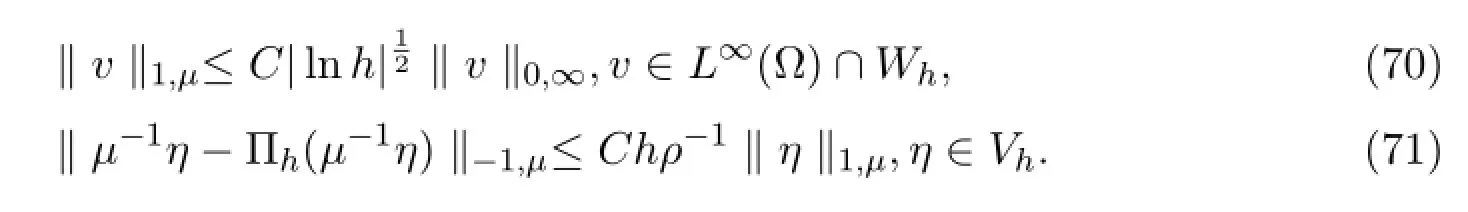
如果v∈Wh是一个固定单元,被选择满足这时

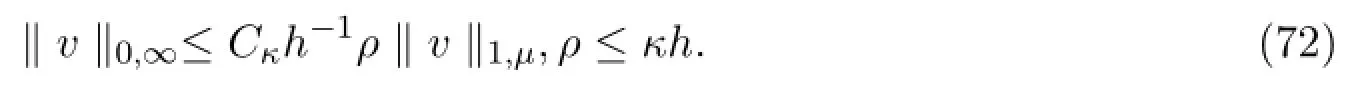
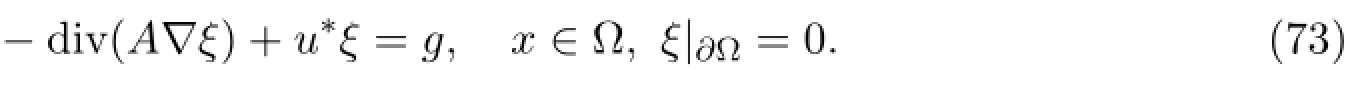
引理3.6[7]令ξ是问题(73)的解.假设Ω是一个凸集.这时有

现在考虑中间变量和投影算子的误差估计.

引理 3.7令和分别是(19)-(22)和(36)-(39)的解.如果解满足：

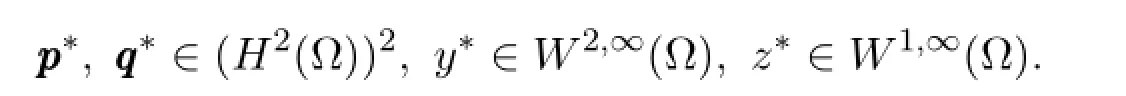
则

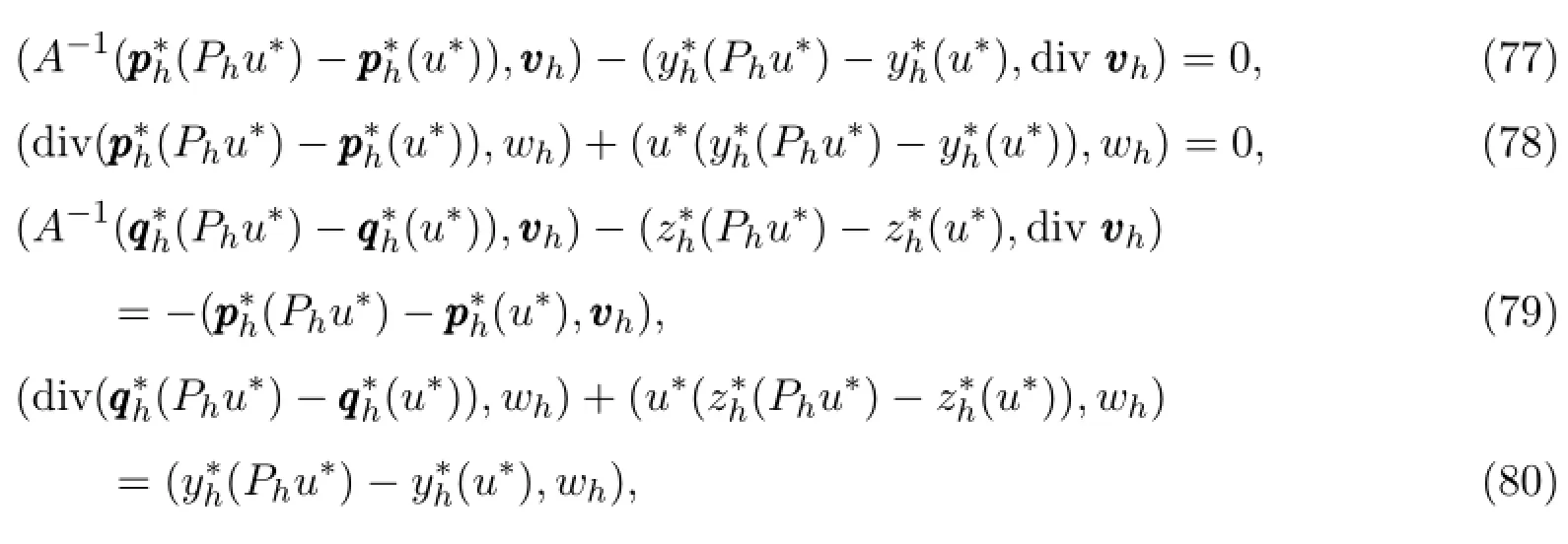
引理 3.8令和分别是问题(36)-(39)中取和的解.这时有

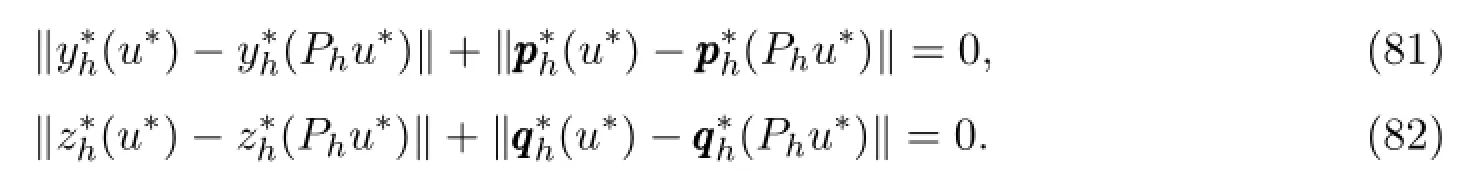
类似于引理3.3,能获得控制变量的L∞-误差估计.

引理 3.9令u∗和分别是问题(19)-(23)和(27)-(31).假设这时有

利用方程(19)-(23)和(27)-(31),得到如下的误差方程：

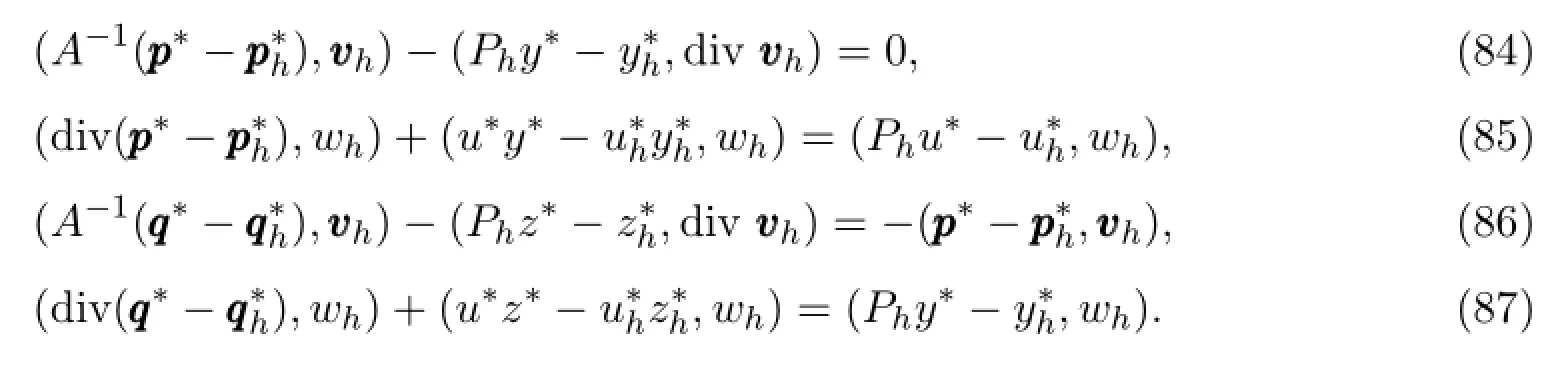
利用类似于引理3.7的证明方法,得到

引理 3.10令和分别是问题(19)-(22)和(27)-(30)的解,这时有

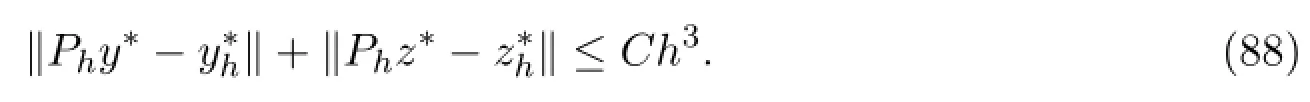
通过修改文献[14]中的定理3.3,能够得到

引理 3.11令和分别是问题(19)-(22)和(27)-(30)的解,这时有

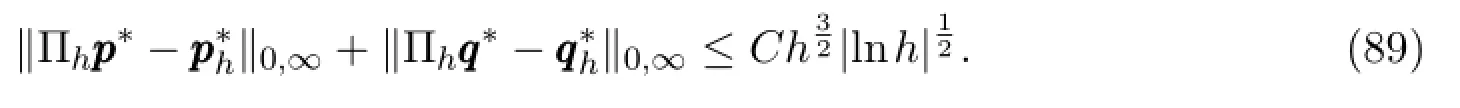
最后,获得状态变量和控制变量的L∞-误差估计.

定理3.1令和分别是问题(19)-(22)和(27)-(30)的解.假设这时有

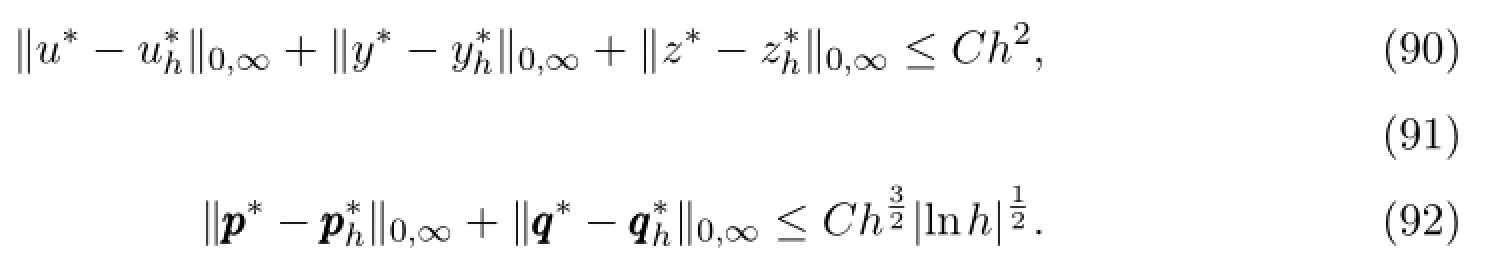
4 数值算例

这一节,将用一个数值算例来验证前面的理论结果,数值算例的程序主要采用了李若教授等人编写的AFEPack软件包[16].考虑如下的等分布参数识别问题：

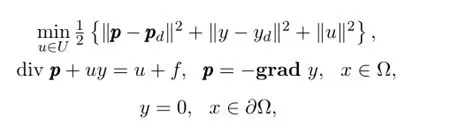
其约束集为U={u∈L∞(Ω)：u(x)≥0}.

接下来,选择如下真解：

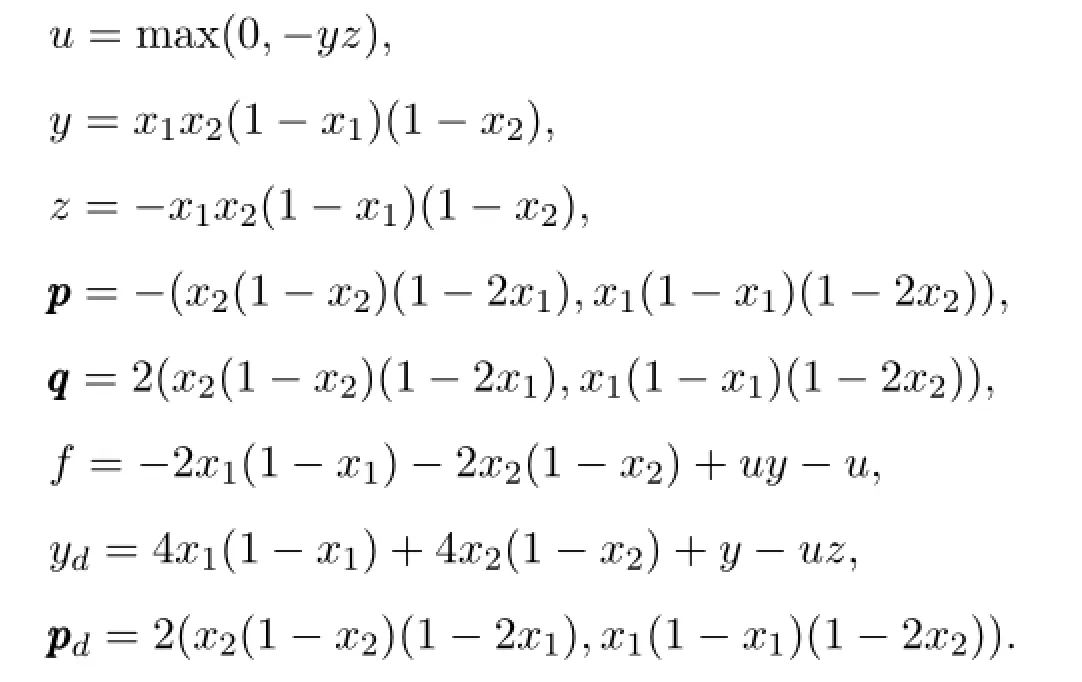
表1 误差‖u∗-u∗h‖0,∞,‖y∗-y∗h‖0,∞和‖z∗-z∗h‖0,∞的收敛阶

表2 误差‖p∗-p∗h‖0,∞和‖q∗-q∗h‖0,∞的收敛阶

[1]Babuška I,Strouboulis T.The Finite Element Method and its Reliability[M].Oxford：Oxford University Press,2001.

[2]Braess D.Finite Elements[M].Berlin Heidelberg：Springer-Verlag,1992.

[3]Brezzi F,Fortin M.Mixed and Hybrid Finite Element Methods[M].Berlin Heidelberg：Springer-Verlag, 1991.

[4]Chen Y,Lu Z,Huang Y.Superconvergence of triangular Raviart-Thomas mixed finite element methods for bilinear constrained optimal control problem[J].Comp.Math.Appl.,2013,66(8)：1498-1513.

[5]Kröner A,Vexler B.A priori error estimates for elliptic optimal control problems with a bilinear state equation[J].Comp.Appl.Math.,2009,230(2)：781-802.

[6]Kunisch K,Liu W,Chang Y,et al.Adaptive finite element approximation for a class of parameter estimation problems[J].J.Comput.Math.,2010,28(5)：645-675.

[7]Kwon Y,Milner F A.L∞-error estimates for mixed methods for semilinear second-order elliptic equations[J].SIAM J.Numer.Anal.,1988,25(1)：46-53.

[8]Li R,Ma H,Liu W.,et al.Adaptive finite element approximation for distributed elliptic optimal control problems[J].SIAM J.Control Optim.,2002,41(5)：1321-1349.

[9]Lu Z,Chen Y.A posteriori error estimates of triangular mixed finite element methods for semilinear optimal control problems[J].Adv.Appl.Math.Mech.,2009,1(4)：242-256.

[10]Lu Z,Chen Y.L∞-error estimates of triangular mixed finite element methods for optimal control problem govern by semilinear elliptic equation[J].Numer.Anal.Appl.,2009,12(1)：74-86.

[11]李鑫.基于新的核函数求解凸二次规划的内点算法[J].重庆三峡学院学报,2016,32(3)：20-24.

[12]Lu Z,Chen Y,Zheng W.A posteriori error estimates of lowest order Raviart-Thomas mixed finite element methods for bilinear optimal control problems[J].East Asia J.Appl.Math.,2012,2(2)：108-125.

[13]Miliner F A.Mixed finite element methods for quasilinear second-order elliptic problems[J].Math.Comp., 1985,44(170)：303-320.

[14]Raviart P A,Thomas J M.A mixed finite element method for 2nd order elliptic problems,math.aspects of the finite element method[J].Lecture Notes in Math.,1977,606(2)：292-315.

[15]Scholz R.A remark on the rate of convergence for a mixed finite element method for second order problems[J].Numer.Funct.Anal.Optim.,1982,4(3)：269-277.

[16]Yang D,Chang Y,Liu W.A priori error estimate and superconvergence analysis for an optimal control problem of bilinear type[J].J.Comput.Math.,2008,26(4)：471-487.

Maximum norm error estimates of mixed finite element solutions for parameters identification problems

Lu Zuliang1,2, Cao Longzhou1, Li Lin1
(1.Key Laboratory for Nonlinear Science and System Structure,Chongqing Three Gorges University, Chongqing 404000,China; 2.Research Center for Mathematics and Economics,Tianjin University of Finance and Economics, Tianjin 300222,China)

In this paper,we investigate maximum norm error estimates of the parameters identification problems by Raviart-Thomas mixed finite element methods.The state and the co-state variables are approximated by the order k=1 Raviart-Thomas mixed finite element spaces and the control variable is approximated by piecewise linear functions.We obtain maximum norm error estimates for the control variable and coupled state variable, the convergence order is h2for the control and state variable andfor co-state variable.The performance of the error estimates is assessed by a numerical example.

parameters identification problems,mixed finite element methods,maximum norm error estimates

O241.82

A

1008-5513(2016)06-0562-12

10.3969/j.issn.1008-5513.2016.06.002

2016-04-01.

国家自然科学基金(11201510,11171251);重庆市高校科研创新团队(CXTDX201601035);中国博士后科学基金(2015M580197);教育部春晖计划(Z2015139);重庆市科委项目(cstc2015jcyjA20001);重庆市万州区科委项目.

鲁祖亮(1980-),博士,教授,研究方向：偏微分方程数值解.

2010 MSC:49J20,65N30