关于完全平方数的一个性质
董祥南
(江西师范大学数学与信息科学学院,江西 南昌 330022)
关于完全平方数的一个性质
董祥南
(江西师范大学数学与信息科学学院,江西 南昌 330022)
运用不定方程的理论讨论了完全平方数的一个基本性质,得到了关于完全平方数的几个重要定理.
不定方程;完全平方数问题;同余;Legendre符号
1 引言与问题的提出
在自然数中,1,4,9,···,n2···是一类很重要的整数,称为完全平方数,古代人从几何图形的角度称其为正方形数-形数的一种[1-4],对这类整数从古代至今已有许多的研究,所得的结论常被用于数列,不定方程和密码信息学的算法分析等问题,例如十八世纪法国的Lagrange就建立了关于完全平方数的一条重要的著名定理[1]:每一个正整数都能表示成至多四个整数的平方和.它用不定方程的术语可以叙述为,对于任意的n∈N,不定方程
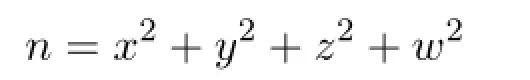
都存在整数解组.本文对完全平方数作了一些简单而基本的讨论,得到了一些这类数的基本性质.具体来讲,研究了如下的问题1:
问题1[5]设n≥2是正整数,n个连续的整数的平方和是完全平方数吗?
2 初步的讨论
注 2.1首先考虑n≥3是奇素数p的情况,此时的问题1是讨论如下不定方程,
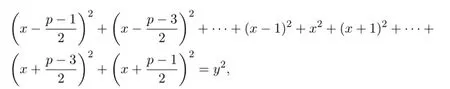
是否存在整数解组(x,y).利用公式
上面的不定方程可以化为
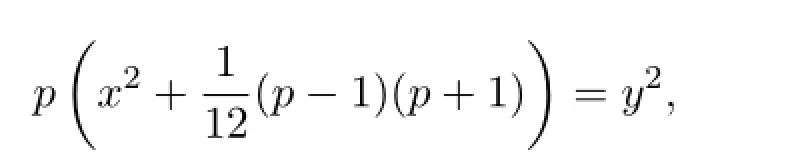
从而归结为不定方程,令y=pz,
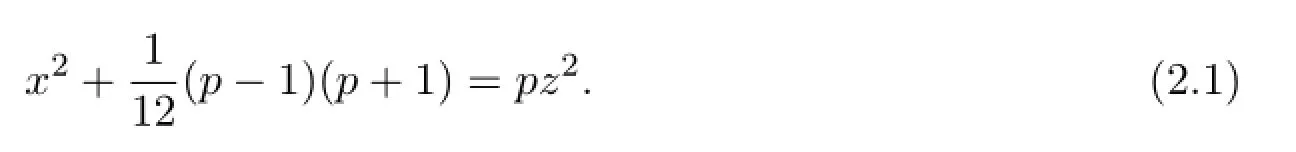
定理2.1设p>2是素数,p=12n+1,则从而有,
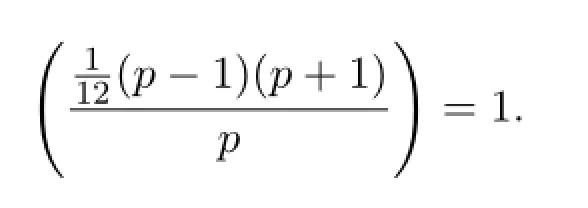


定理2.2设p>2是素数,p=12n+5,n是偶数,则
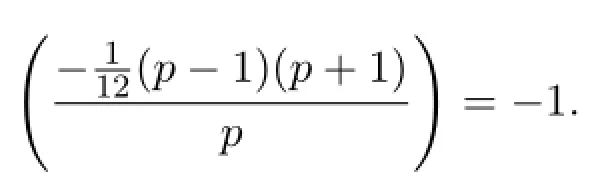
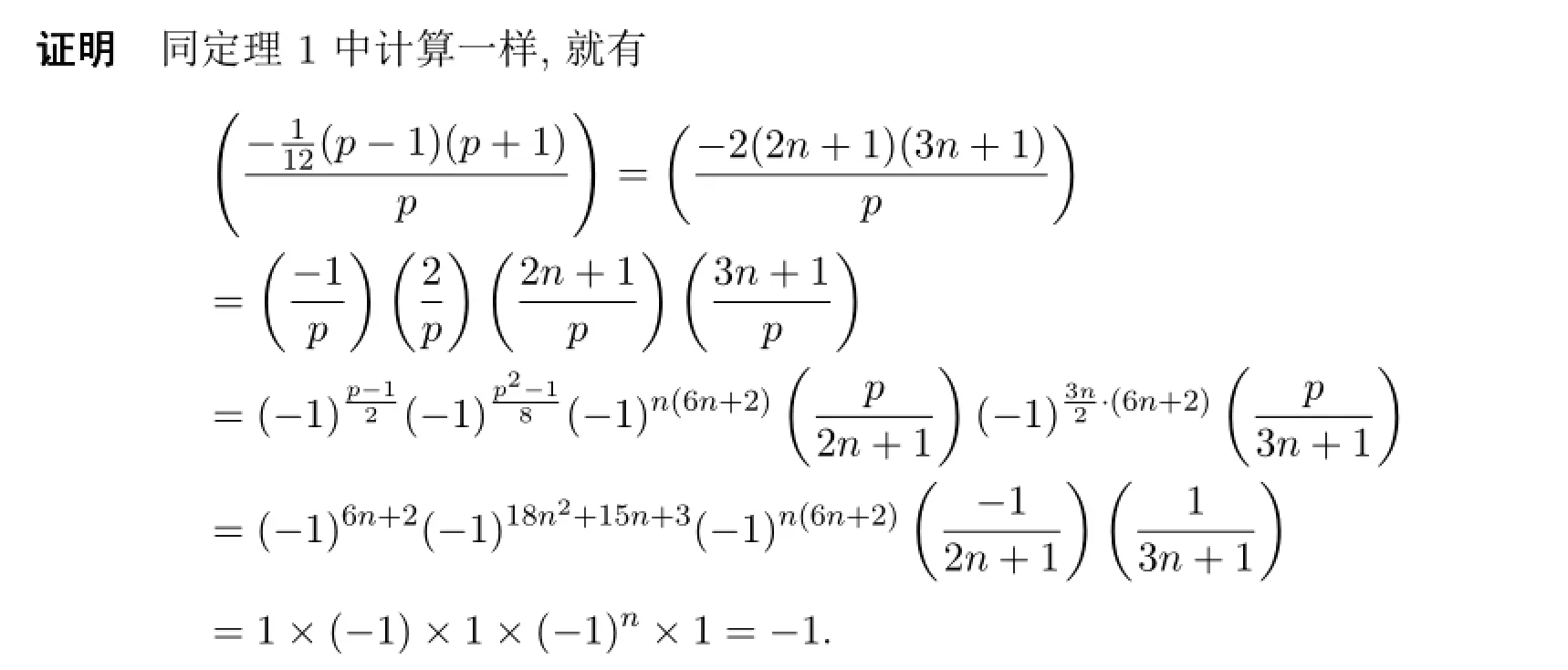
推论2.1设p≡5(mod 24)是素数,则p个连续整数的平方和不可能是完全平方数.


注 2.2由推论2.1,当p=5,29,53,101,149,173,197,293,317,389,461,509,557,653,···时,p个连续整数的平方和不可能是完全平方数.
定理2.3设p>2是素数,p=12n+7,n是奇数,则

推论2.2设p≡19(mod 24)是素数,则p个连续整数的平方和不可能是完全平方数.
证明与推论2.1的证明完全类似,此处略.
注2.3由推论2.2可知,当p=19,43,67,139,163,211,283,307,331,379,499,523,547,571,619,···时,p个连续整数的平方和不可能是完全平方数.
和上面一样讨论,我们也可以得到下列结论:
定理2.4设p>2是素数,
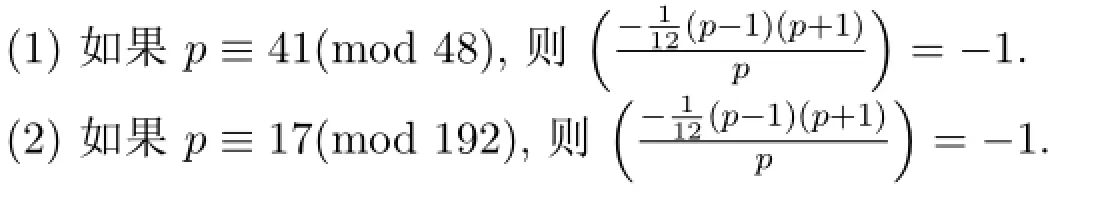
推论2.3设p>2是素数,p≡41(mod 48)或p≡17(mod 192),则p个连续整数的平方和不可能是完全平方数.
注 2.4由推论2.3,当p=41,89,137,233,281,521,569,617,···或p=17,401,593,···时,p个连续整数的平方和不可能是完全平方数.
定理2.5设p>2是素数,p≡7(mod 48),则
推论2.4设p>2是素数,p≡7(mod 48),则p个连续整数的平方和不可能是完全平方数.
注 2.5由推论2.4,当p=7,103,151,199,439,487,631,···时,p个连续整数的平方和不可能是完全平方数.
注 2.6由上面的讨论我们可以看出,对许多的奇素数p>2,p个连续整数的平方和不可能是完全平方数,似乎有理由提出如下的猜测:设p是任意奇素数,则p个连续整数的平方和不可能是完全平方数.遗憾的是,这个猜测是不正确的,我们已经发现了如下的一些反例,
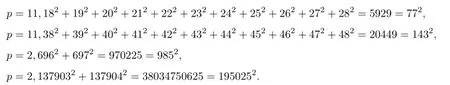
另一方面,用模3分类的方法可以证明3个连续整数的平方和不可能是完全平方数(比前面的方法更简单),也同样可以证明p=13,31,79,107,113,127,223,257,271,311,353,367,463时,p个连续整数的平方和不可能是完全平方数,但是因p=3,13,31,79,107,113,127,223,257,271,311,353,367,463这几个素数却不在上面几个定理中讨论的素数p的范围内,因此,除了推论2.1,推论2.2,推论2.3以及推论2.4中的那些素数外,在剩余的素数中,还有哪些素数p,使得p个连续整数的平方和不可能是完全平方数?更具体地来讲,在300以内的素数中,在p= 23,37,47,59,61,71,73,83,97,109,131,157,167,179,181,191,193,227,229,239,241,251,263,277这24个素数中,哪几个素数p使得p个连续整数的平方和不可能是完全平方数?这是一个有意义的值得进一步研究讨论的问题.
3 进一步的讨论
下面考虑问题1中n不是素数p的情形.

定理3.1设p≡5(mod 24)是素数,则p3个连续整数的平方和不可能是完全平方数.


定理3.2设p≡19(mod 24)是素数,则p3个连续整数的平方和不可能是完全平方数.

注3.1由定理3.1可知,当p=5,29,53,101,149,173,197,269,293,317,389,461,509,557,653,···时,p3个连续整数的平方和不可能是完全平方数.
注3.2由定理3.2可知,当p=19,43,67,139,163,211,283,307,331,379,499,523,547,571,619,···时,p3个连续整数的平方和不可能是完全平方数.
完全类似地,可以证明:
定理3.3设p≡7(mod 48)是素数,则p3个连续整数的平方和不可能是完全平方数.
定理3.4设p≡41(mod 48)是素数,则p3个连续整数的平方和不可能是完全平方数.
注 3.3由定理3.3可知,当p=7,103,151,199,487,631,···时,p3个连续整数的平方和不可能是完全平方数.
注 3.4由定理3.4可知,当p=41,89,137,233,281,521,569,617,···时,p3个连续整数的平方和不可能是完全平方数.
定理3.5设p≡17(mod 192)是素数,则p3个连续整数的平方和不可能是完全平方数.
注 3.5由定理3.5可知,当p=17,401,593,···时,p3个连续整数的平方和不可能是完全平方数.
再次,设p和q是两个不相等的奇素数,令
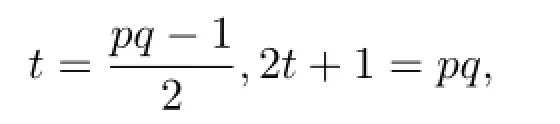
则
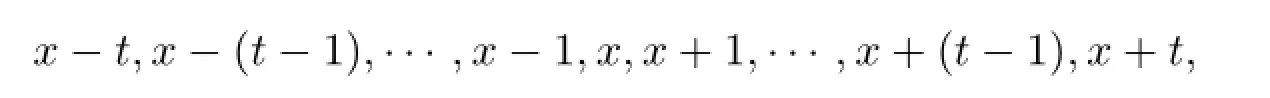
是2t+1个连续的整数,如果其平方和是完全平方数,则和前面一样处理可以导出不定方程,

直接计算可得,
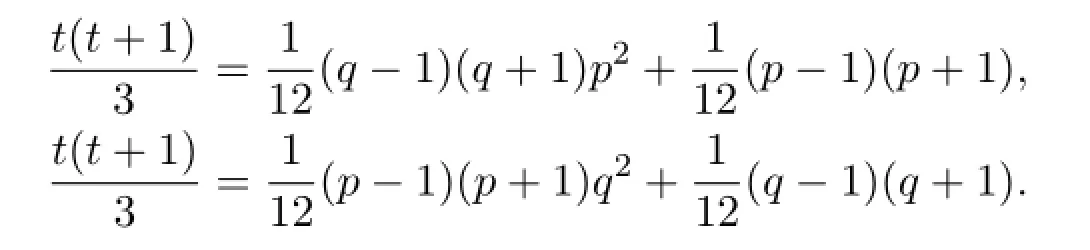
定理3.6设p是奇素数,p满足下列条件之一,
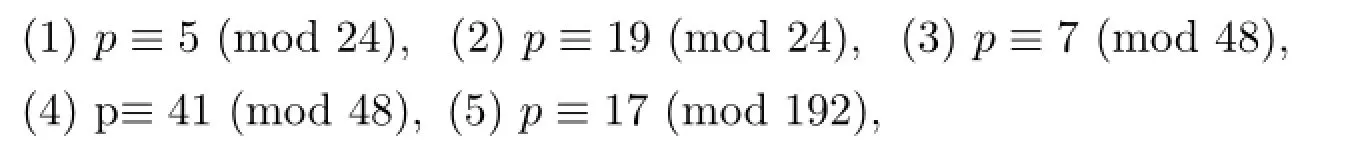
q是不等于p的奇素数,则pq个连续整数的平方和不可能是完全平方数.

定理3.7设定理3.6中p,q位置互换,则定理结论任然成立.
注 3.6设p≡5(mod 24)是奇素数,即p=24n+5,则令
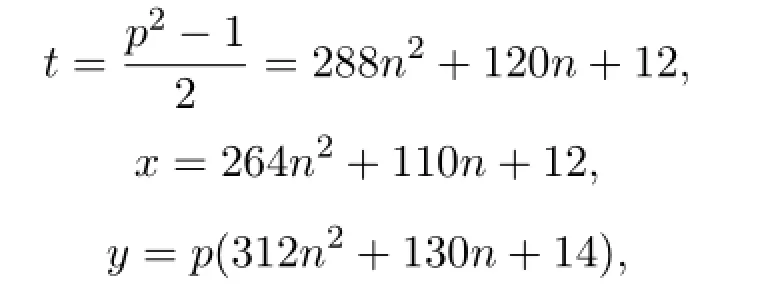
则有
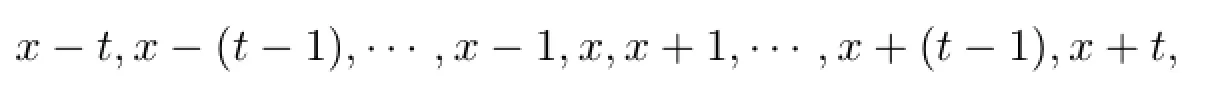
这连续的2t+1=p2个整数的平方和是整数y的平方,即有
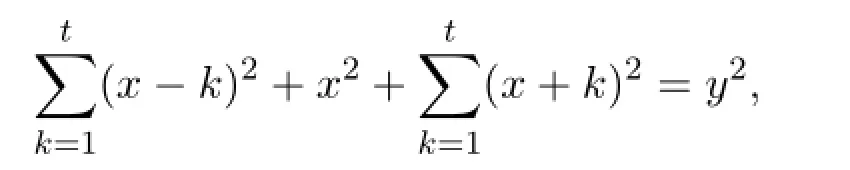
这说明当p≡5(mod 24)时,p2个连续整数的平方和可以是某个整数的平方.
参考文献
[1]闵嗣鹤,严士键.初等数论[M].2版.北京:高等教育出版社,1982.
[2]Silverman J H.数论概貌[M].3版.北京:机械工业出版社,2008.
[3]柯召,孙琦.数论讲义:上册[M].北京:高等教育出版社,2001.
[4]Rosen K H.初等数论及其应用[M].5版.夏鸿刚,译.北京:机械工业出版社,2009.
[5]董祥南.关于模椭圆曲线上的格点计算[J].江西科学,2014,32(2):202-266.
[6]南开大学数学系.世界数学奥林匹克解题大辞典[M].石家庄:河北少年儿童出版社,2012.
[7]Chen J H,Paul V.Complete solution of the Diophantine equation X2+1=dY4and a related family of quartic Tude equations[J].J.Number Theory,1997,62(1):71-99.
[8]Walsh G.A note on a theorems of Ljunggren and the Diophantine equations x2-kxy2+y4=1[J].Arch.Math.,1999,73(2):119-125.
On some properties of perfect square numbers
Dong Xiangnan
(Mathematics and Information Science College of Jiangxi Normal University,Nanchang 330022,China)
In this paper some basic properties of perfect square numbers was discussed by the theory of indeterminate equations,and we obtained several important theorem about the perfect square numbers.
perfect square numbers,indeterminate equation problems,congruence Legendre symbol
O156.4
A
1008-5513(2016)06-0574-09
10.3969/j.issn.1008-5513.2016.06.003
2016-07-29.
江西省自然科学基金(JXNF20140405A01).
董祥南(1968-),硕士,副教授,研究方向:初等数论及其应用.
2010 MSC:11B68

