区间数的绝对值与区间值函数的极限

代兵,包玉娥

(内蒙古民族大学数学学院,内蒙古 通辽 028043)

区间数的绝对值与区间值函数的极限

代兵,包玉娥

(内蒙古民族大学数学学院,内蒙古 通辽 028043)

研究了区间数的绝对值和区间值函数的极限问题.首先,讨论了区间数的H-差的性质,得到了H-差的两个运算法则;然后,给出了区间数的绝对值概念,并讨论了区间数绝对值的性质;最后,借助区间数的H-差和绝对值的概念,建立了区间值函数极限概念的一种新的表达方式,给出了极限存在的充分必要条件,证明了极限值的唯一性及对加法运算和数乘运算的封闭性.

区间数;H-差;绝对值;区间值函数;极限

1 引言

区间数理论的基本思想是应用区间数变量代替点变量进行计算.早在1931年Young[1]就开始了区间数理论的研究.之后,由Moore[2]为代表的众多学者的共同努力下,区间数的理论及应用有很大的发展.特别是,为了建立区间值微分方程理论[3],区间值最优化理论[4]以及模糊值函数的微分理论[5]等,利用不同的方式引进了各种不同的微分概念及相关性质.文献[3-6]引进了区间值函数的微分概念及相关性质.在这些研究工作中,区间数差的概念及区间值函数的极限概念起了重要作用.其中,文献[4]利用区间数的Hausdorff距离讨论了区间值函数的极限问题,给出了相关的性质.文献[7]通过引进区间数模的概念,给出了区间值函数的极限概念及其相关性质.本文在文献[8-9]的基础上,研究了模糊值函数的次可微性及相关问题,得到了一些有意义的结论.

本文尝试借助区间数的H-差和绝对值的概念,利用实分析的方法建立区间值函数的极限概念及相关性质.希望对研究区间值函数及模糊值函数的微分理论及其应用问题提供一种新的思想方法.

2 区间数的基本概念

本节介绍区间数的相关概念,并讨论H-差（Hukuhara差）的一些性质.

下面首先介绍区间数的加法运算、数乘运算及大小关系.内容来自文献[10].

定义2.1[4]对于a,b∈[R],如果存在c∈[R],使得a=b+c,则称c为a与b的H-差,记为c=a-Hb.

注2.1对于a,b∈[R],若a-Hb存在,则

定理2.1设a,b,c,d∈[R],若a-Hc,b-Hd都存在,则H-差(a+b)-H(c+d)也存在且有

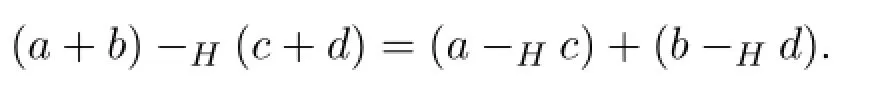
定理2.2设a,b∈[R]且k＞0,若H-差a-Hb存在,则H-差ka-Hkb存在且

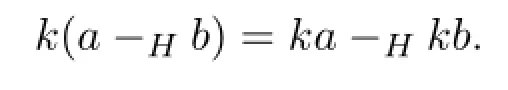
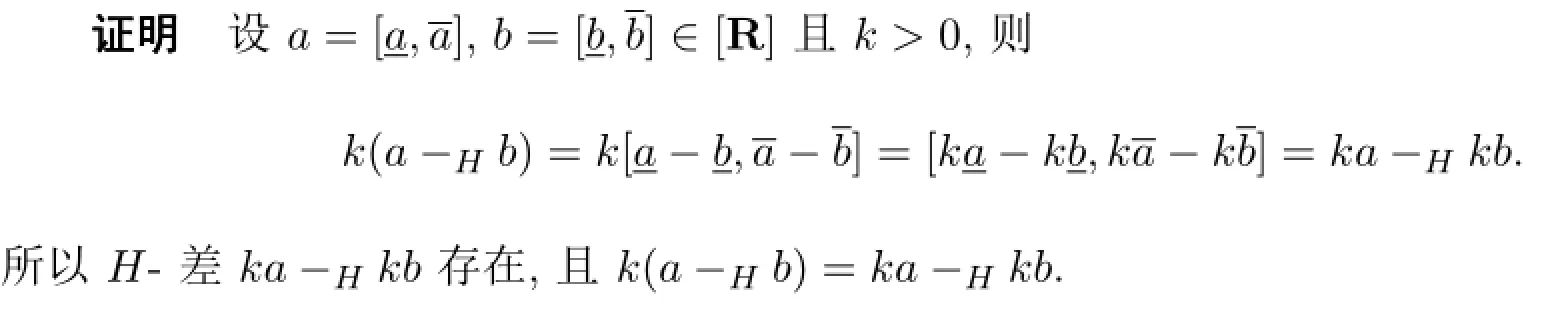
3 区间数的绝对值

本节给出区间数绝对值的概念,并讨论它的一些性质.

定义3.1设则区间数a的绝对值定义为

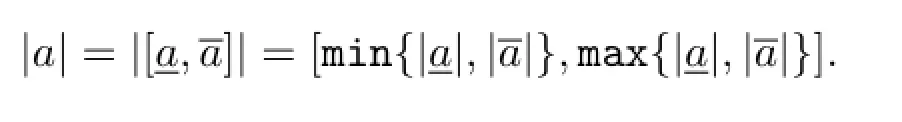
注 3.1由定义2.1,我们易推出下面的结论：

(1)|a|=|-a|;

(2)当a∈[R+]时,|a|=a;当a∈[R-]时,|a|=-a;

(3)当k≥0时,|ka|=k|a|;当k＜0时,|ka|=-k|a|.

定理3.1设a,b∈[R+]或a,b∈[R-],则有

(1)|a+b|≤|a|+|b|;

(2)当H-差a-Hb存在时,|a-Hb|≤|a|+|b|;

(3)当H-差a-Hb和|a|-H|b|都存在时,|a-Hb|≥|a|-H|b|;

(4)当|a|-H|b|存在时,|a|-H|b|≤|a+b|.

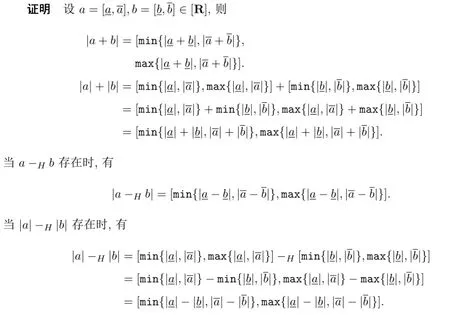
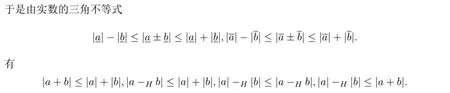
定理 3.2设a,b∈[R],对任意ε=[ε,ε]∈[R+],若H-差a-Hb存在且|a-Hb|≤ε,则a=b.

定理3.3设a,b∈[R],若H-差a-Hb存在且|a-Hb|=[0,0],则a=b.

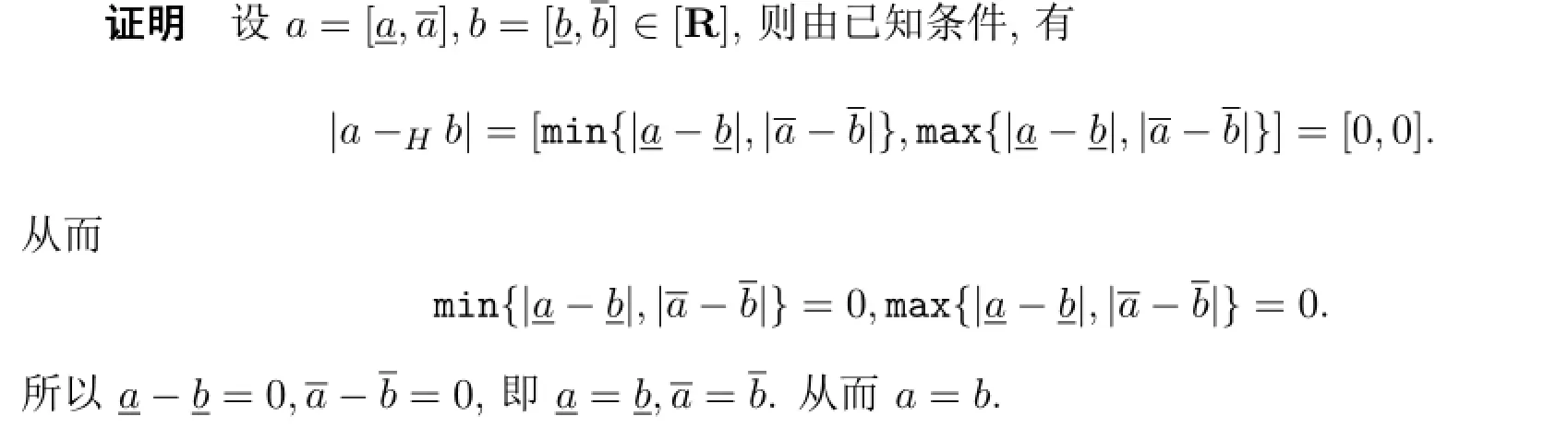
定理3.4设a,b∈[R],若H-差a-Hb和b-Ha都存在，则

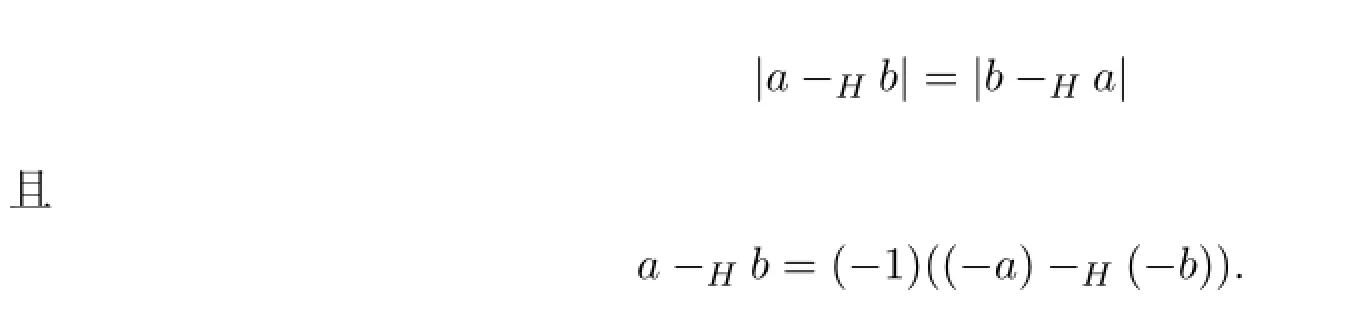
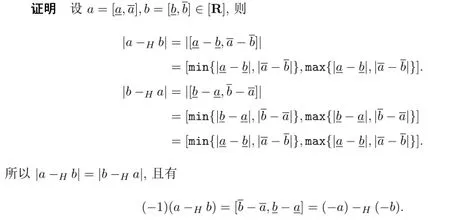
定理 3.5设a,b,c∈[R],若H-差a-Hc和c-Hb都存在,则H-差a-Hb存在,且a-Hc和c-Hb都为正区间数或负区间数时,有

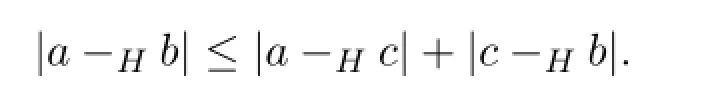
4 区间值函数的极限

本节讨论正区间值函数的极限问题.在本节中设U0(x0)为x0的某空心邻域,定义在U0(x0)上的区间值函数f：U0(x0)→[R]为

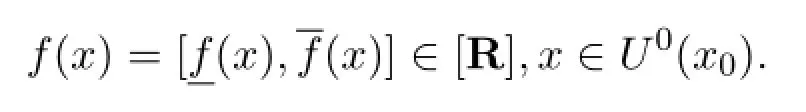
定义4.1 设f：U0(x0)→[R+]为区间值函数,且A∈[R].如果对任意ε=[ε,ε]∈[R+],存在δ＞0,当0＜|x-x0|＜δ时,H-差f(x)-HA和A-Hf(x)都存在,且

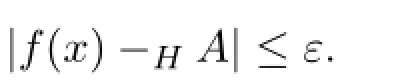
则称f(x)在点x0处极限存在且极限值为A,并记为

定理 4.1设f(x)为定义在U0(x0)内的区间值函数且A∈[R],则的充要条件是

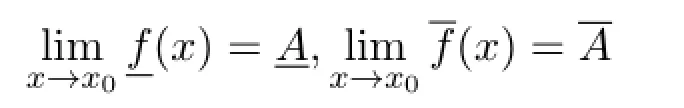
且存在δ＞0,当0＜|x-x0|＜δ时,H-差f(x)-HA和A-Hf(x)都存在.

定理4.2若区间值函数f(x)在点x0处极限存在,则它有唯一的极限.

定理4.4设f(x),g(x),h(x)为定义在U0(x0)内的三个区间值函数且

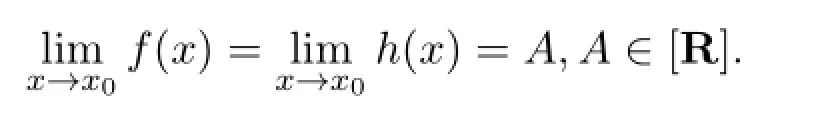
如果存在δ＞0,当0＜|x-x0|＜δ时,有f(x)≤g(x)≤h(x)且H-差g(x)-HA和A-Hg(x)都存在,则又因为存在δ＞0,当0＜|x-x0|＜δ时,有f(x)≤g(x)≤h(x).

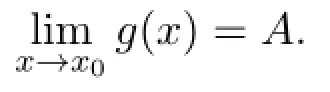
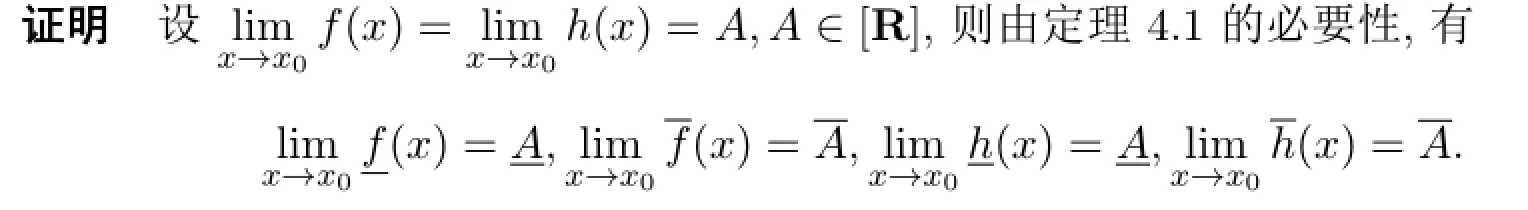
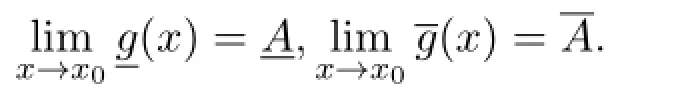
又因为当0＜|x-x0|＜δ时,H-差g(x)-HA和A-Hg(x)都存在.

[1]Yang R C.The algebra of many-valued quantities[J].Annals of Mathematics,1931,31：260-290.

[2]Moor R E.Interval Analysis[M].New Jersey：Prentice Hall,1966.

[3]Luciano Stefanini,Barnabas Bede.Generalized Hukuhara differentiability of interval-valued functions and interval differetial equations[J].Noninear Analysis,2009,71：1311-1328.

[4]Wu Hsien chung.The Karush-Kuhn-Tucker optimality conditions in multiobjective programming problems with interval-valued objective functions[J].European Journal of Operational Research,2009,196：49-60.

[5]Barnabas Bede,Luciano Stefanini.Generalized differentiability of fuzzy-valued functions[J].Fuzzy Sets and Systems,2013,230：119-141.

[6]Chalco-Cano Y,Rufian-Lizana A,Ronman-Flores H,et al.Calculs for interval-valued functions using generalized Hukuhara derivative and applications[J].Fuzzy Sets and Systems,2013,219：49-67.

[7]Vasile Lupulescu.Fractional calculus for interval-valued functions[J].Fuzzy Sets and Systems,2015,265：63-85.

[8]关世霞,包玉娥,赵慧冬.模糊值函数的凸性与次微分性[J].纯粹数学与应用数学,2012,28(5)：676-686.

[9]包玉娥,赵博,彭晓芹.关于模糊值凸函数的共轭问题的研究[J].纯粹数学与应用数学,2013,29(4)：331-337.

[10]胡启洲,张卫华.区间数理论的研究及其应用[M].北京：科学出版社,2010.

The absolute value of interval numbers and the limit of the interval value function.

Dai Bing,Bao Yu′e
(College of Mathematics,Inner Mongolia University for the Nationalities,Tongliao 028043,China)

In this paper,we study the absolute value of interval numbers and the limit of the interval value function.First of all,we discuss the properties of H-difference of interval numbers,achieve two rules of algorithm of H-difference.Then,we propose the concept of the absolute value of interval numbers,and discuss the properties of the absolute value of interval numbers.In the end,we set up a new expression the concept of the limit of interval value function with the help of the concept of H-difference and absolute value of interval number,conclude the sufficient condition of the existence of limit,and proves the uniqueness of limit value and the sealing ability of addition and multiplication operation.

interval numbers,H-difference,absolute value,interval value function,limit

0159.2

A

1008-5513(2016)06-0583-08

10.3969/j.issn.1008-5513.2016.06.004

2016-07-10.

国家自然科学基金(11461052);内蒙古自然科学基金(2014MS0107).

代兵(1991-),硕士生,研究方向：不确定数学理论及其应用.

包玉娥(1962-),博士,教授,研究方向：不确定数学理论及其应用.

2010 MSC:03E72