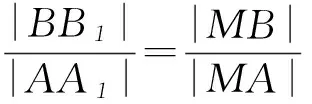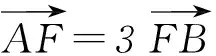解题训练中典型例题的选择
◇ 江西 袁人兵
解题训练中典型例题的选择
◇ 江西 袁人兵
有效的解题训练是提高学生分析问题、解决问题能力的重要途径.那么选择什么样的习题,才能起到有效训练的目的?本文以抛物线的学习为例,介绍几种例题的选择视角与读者分享.
1 要有利于巩固基础知识
例1已知点P是抛物线y2=2x上的一个动点,则点P到点A(0,2)的距离与点P到该抛物线准线的距离之和的最小值为( ).
解析设点P在准线上的射影为P′,由抛物线定义得|PP′|=|PF|,则
|PF|+|PA|=|PP′|+|PA|.
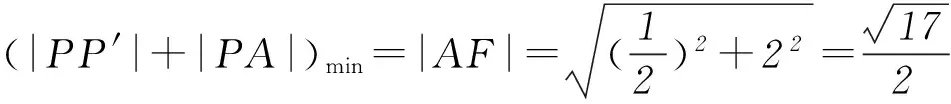
点评对双基的考查一直是高考命题的一个重要方向.双基是指基础知识和基本方法,因此例题的选择要有助于学生对基础知识的掌握以及对基本方法的灵活应用.本题求解中首先根据抛物线的定义将点P到准线的距离|PP′|转化为|PF|,再利用3点共线解决问题.
2 要有利于体现知识点间的联系
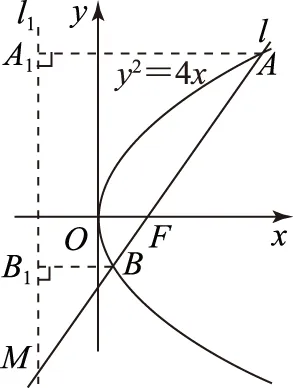
例2已知点A(x1,y1)、D(x2,y2) (其中x1 (1) 当点B的坐标为(1,0)时,求直线AD的斜率; (2) 记△OAD的面积为S1,梯形ABCD的面积为S2,求证:S1/S2<1/4. (1) 当点B坐标为(-1,0)时,求k的值; (2) 记△OAD的面积S1,四边形ABCD的面积为S2. (ⅱ) 求证:S1/S2≥1/2. 点评圆锥曲线包括椭圆、双曲线和抛物线,三者无论是从定义(第二定义),还是相关性质上都有其相似性,因此对于适合其中某一种曲线的性质,往往都可以类比推理到其他曲线.上述2例无论从命题形式,还解题方法上看,都有异曲同工之妙. 下面给出例3的解析过程: 解析(1)因为B(-1,0),所以A(-1,y0),代入x2/4+y2/3=1 (y≥0),解得y0=3/2,代入直线y=kx+1,得k=-1/2. 所以 而y1+y2=kx1+1+kx2+1=k(x1+x2)+2,所以 例5(逆向变换)抛物线C:y2=4x的焦点为F,直线l过F且与C交于A、B2点.若|AF|=3|BF|,则l的方程为( ). Ay=x-1或y=-x+1; 例6(拓展变换) 设F为抛物线C:y2=3x的焦点,过F且倾斜角为30°的直线交C于A、B2点,O为坐标原点,则△OAB的面积为____.(答案:9/4) 点评一题多变通常从改变问题的条件、改变问题的结论(如例6)、条件与结论互换(如例5与例4)等视角来实现.对些类问题的训练能有效考查学生灵活应用所学知识解决问题的能力. 例7同例5 图1 解法1如图1所示,作出抛物线的准线l1及点A、B到准线的垂线段AA1、BB1,并设直线l交准线于点M.设|BF|=m. 由抛物线的定义可知|BB1|=m,|AA1|=|AF|=3m. 点评解析几何具有代数与几何的双重身份,解题中即可以从几何角度入手,挖掘解析几何的几何本质.也可从数的角度入手,即通过坐标法,实现几何问题的代数化求解.本题从几何与代数2种视角实现了对问题的解答. 江西省赣州市南康区第四中学)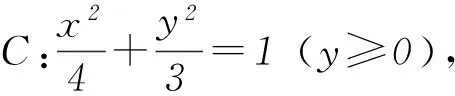
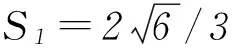
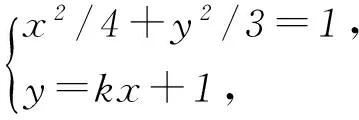
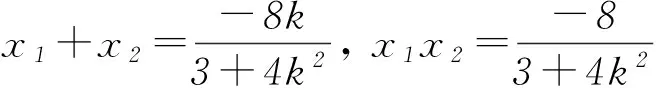
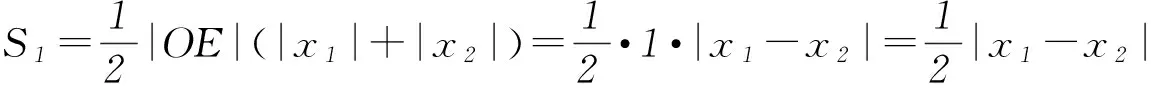
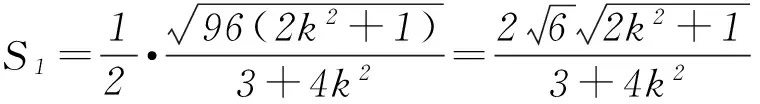
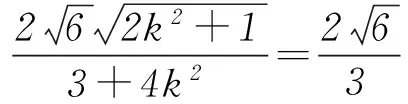
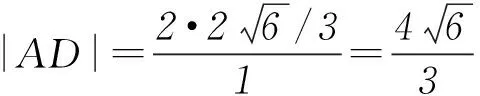
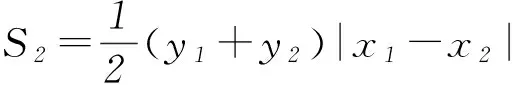
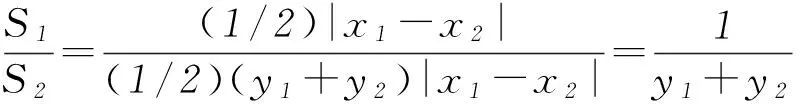
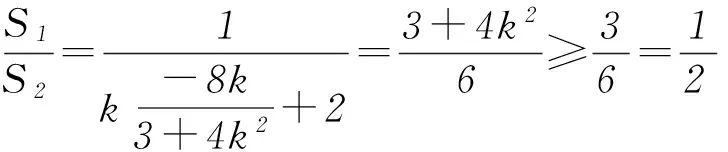
3 一题多变的例题有利于学生知识系统化
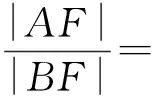
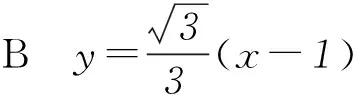
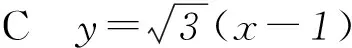
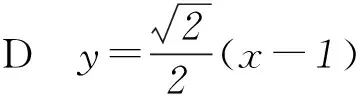
4 典型例题有利于总结解题方法